6.1.1反比例函数 课件(共14张PPT)浙教版八年级下册
文档属性
| 名称 | 6.1.1反比例函数 课件(共14张PPT)浙教版八年级下册 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-05 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
反比例函数
6.1
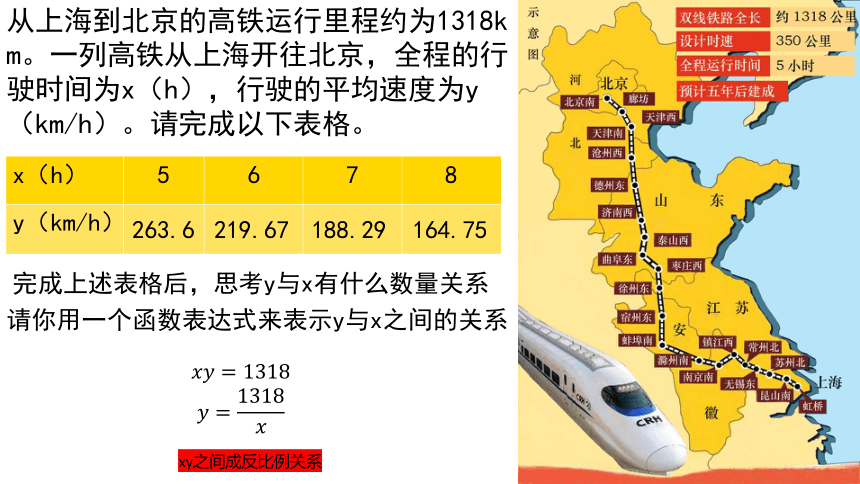
从上海到北京的高铁运行里程约为1318km。一列高铁从上海开往北京,全程的行驶时间为x(h),行驶的平均速度为y(km/h)。请完成以下表格。
x(h) 5 6 7 8
y(km/h)
263.6
219.67
188.29
164.75
完成上述表格后,思考y与x有什么数量关系
请你用一个函数表达式来表示y与x之间的关系
xy之间成反比例关系
下表是测量质量都是100g的金、铜、铁、铝四种金属块的体积x(cm )的结果,y(g/cm3)表示金属块的密度. 已知锌的密度是7.14g/cm3,金的密度是19.30g/cm3.请完成以下表格
金属 相关量 金 铜 铁 锌 铝
x(cm3) 5.18 11.21 12.82 35.84
y(g/cm3) 19.30 7.14
8.92
7.80
14.01
2.79
完成上述表格后,思考y与x有什么数量关系
请你用一个函数表达式来表示y与x之间的关系
y=
xy之间成反比例
提炼概念
在前面两个例题中的函数具有怎样的共同特征?
2.y=
xy乘积为定值
我们把函数 y=(k为常数,k≠0)叫做反比例函数.
这里x是自变量,y是关于x的函数
k是比例系数
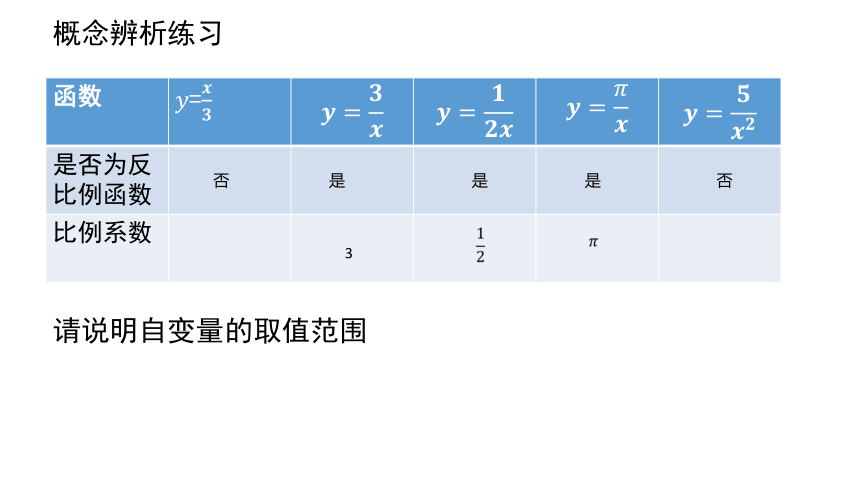
概念辨析练习
函数 =
是否为反比例函数
比例系数
请说明自变量的取值范围
是
否
是
是
否
3
例1 如图,阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(图中杠杆本身所受重力略去不计.杠杆平衡时:动力×动力臂=阻力×阻力臂).(1)求y关于x的函数解析式.这个函数是反比例函数吗 如果是,请说出比例系数;(2)求当x=50时,函数y的值,并说明这个值的实际意义(3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n(n>1)倍时,所需动力将怎样变化?
解:(1)yx=1000×5=5000
所以所求函数的表达式为
这个函数是反比例函数,比例系数是5000.
(2)当x=50时,
这个函数值的实际意义是,当动力臂长为50cm时,所需动力为100(N).
(3)设原来的动力臂为d(cm),动力为y1(N);扩大后的动力臂长为nd(cm)(n>1),动力为y2(N). 将x=d,x=nd分别代入
得
所以当动力臂长扩大到原来的n倍时,所需动力缩小到原来的 .
练习
C
追问:上述反比例函数的比例系数为
变式
下列函数中,哪些是反比例函数?是反比例函数,指出其比例系数和自变量的取值范围
(1) (2) (3) (4)
2.下列选项中的两个变量成反比例函数关系的是 ( )
A.三角形的高不变,它的底边长和面积
B.圆柱的体积一定,它的底面积和高
C.汽车速度不变,它行驶的路程与时间
D.苹果的单价一定,它的总价与数量
你还能举出其它类似的例子吗
B
3.某商场出售一批进价为每张2元的贺卡,在市场营销中发现此贺卡的日销售单价x(元)与日销售量y(张)之间有如下关系:
日销售单价x(元) … 3 4 5 6 …
日销售量y(张) … 20 15 12 10 …
则y与x之间的函数关系式为 .
你是如何判断的,两个变量符合反比例函数的关系,则两个变量有什么关系
乘积为定值
4.已知一个长方体的体积是100 立方厘米,它的长是y cm,宽是10 cm,高是x cm.
(1)写出y与x之间的函数关系式;
(2)当x=2时,求y的值,并说明这个值的实际意义;
(3)利用y关于x的函数表达式,说明当高扩大到原来的n(n>1)倍时,长将怎样变化.
(3)利用y关于x的函数表达式,说明当高扩大到原来的n(n>1)倍时,长将怎样变化.
5.函数______
中考原题再现
6.若函数y=(m+1)xm +3m+1是反比例函数,求m的值.
-1
课堂总结
本节课你学到了什么?
2.其中x是自变量,y是x的函数,k是比例系数
1.一般地,形如 (k是常数,k≠0)的函数叫做反比例函数.
3.反比例函数的自变量x的取值不能为零。
4.反比例函数的三种形式
反比例函数
6.1
从上海到北京的高铁运行里程约为1318km。一列高铁从上海开往北京,全程的行驶时间为x(h),行驶的平均速度为y(km/h)。请完成以下表格。
x(h) 5 6 7 8
y(km/h)
263.6
219.67
188.29
164.75
完成上述表格后,思考y与x有什么数量关系
请你用一个函数表达式来表示y与x之间的关系
xy之间成反比例关系
下表是测量质量都是100g的金、铜、铁、铝四种金属块的体积x(cm )的结果,y(g/cm3)表示金属块的密度. 已知锌的密度是7.14g/cm3,金的密度是19.30g/cm3.请完成以下表格
金属 相关量 金 铜 铁 锌 铝
x(cm3) 5.18 11.21 12.82 35.84
y(g/cm3) 19.30 7.14
8.92
7.80
14.01
2.79
完成上述表格后,思考y与x有什么数量关系
请你用一个函数表达式来表示y与x之间的关系
y=
xy之间成反比例
提炼概念
在前面两个例题中的函数具有怎样的共同特征?
2.y=
xy乘积为定值
我们把函数 y=(k为常数,k≠0)叫做反比例函数.
这里x是自变量,y是关于x的函数
k是比例系数
概念辨析练习
函数 =
是否为反比例函数
比例系数
请说明自变量的取值范围
是
否
是
是
否
3
例1 如图,阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(图中杠杆本身所受重力略去不计.杠杆平衡时:动力×动力臂=阻力×阻力臂).(1)求y关于x的函数解析式.这个函数是反比例函数吗 如果是,请说出比例系数;(2)求当x=50时,函数y的值,并说明这个值的实际意义(3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n(n>1)倍时,所需动力将怎样变化?
解:(1)yx=1000×5=5000
所以所求函数的表达式为
这个函数是反比例函数,比例系数是5000.
(2)当x=50时,
这个函数值的实际意义是,当动力臂长为50cm时,所需动力为100(N).
(3)设原来的动力臂为d(cm),动力为y1(N);扩大后的动力臂长为nd(cm)(n>1),动力为y2(N). 将x=d,x=nd分别代入
得
所以当动力臂长扩大到原来的n倍时,所需动力缩小到原来的 .
练习
C
追问:上述反比例函数的比例系数为
变式
下列函数中,哪些是反比例函数?是反比例函数,指出其比例系数和自变量的取值范围
(1) (2) (3) (4)
2.下列选项中的两个变量成反比例函数关系的是 ( )
A.三角形的高不变,它的底边长和面积
B.圆柱的体积一定,它的底面积和高
C.汽车速度不变,它行驶的路程与时间
D.苹果的单价一定,它的总价与数量
你还能举出其它类似的例子吗
B
3.某商场出售一批进价为每张2元的贺卡,在市场营销中发现此贺卡的日销售单价x(元)与日销售量y(张)之间有如下关系:
日销售单价x(元) … 3 4 5 6 …
日销售量y(张) … 20 15 12 10 …
则y与x之间的函数关系式为 .
你是如何判断的,两个变量符合反比例函数的关系,则两个变量有什么关系
乘积为定值
4.已知一个长方体的体积是100 立方厘米,它的长是y cm,宽是10 cm,高是x cm.
(1)写出y与x之间的函数关系式;
(2)当x=2时,求y的值,并说明这个值的实际意义;
(3)利用y关于x的函数表达式,说明当高扩大到原来的n(n>1)倍时,长将怎样变化.
(3)利用y关于x的函数表达式,说明当高扩大到原来的n(n>1)倍时,长将怎样变化.
5.函数______
中考原题再现
6.若函数y=(m+1)xm +3m+1是反比例函数,求m的值.
-1
课堂总结
本节课你学到了什么?
2.其中x是自变量,y是x的函数,k是比例系数
1.一般地,形如 (k是常数,k≠0)的函数叫做反比例函数.
3.反比例函数的自变量x的取值不能为零。
4.反比例函数的三种形式
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
