反比例函数知识点及经典练习

反比例函数
一、基础知识
定义：一般地，形如（为常数，）的函数称为反比例函数。还可以写成
反比例函数解析式的特征：
⑴等号左边是函数，等号右边是一个分式。分子是不为零的常数（也叫做比例系数），分母中含有自变量，且指数为1.
⑵比例系数
⑶自变量的取值为一切非零实数。
⑷函数的取值是一切非零实数。
反比例函数的图像
⑴图像的画法：描点法
列表（应以O为中心，沿O的两边分别取三对或以上互为相反的数）
描点（有小到大的顺序）
连线（从左到右光滑的曲线）
⑵反比例函数的图像是双曲线，（为常数，）中自变量，函数值，所以双曲线是不经过原点，断开的两个分支，延伸部分逐渐靠近坐标轴，但是永远不与坐标轴相交。
⑶反比例函数的图像是是轴对称图形（对称轴是或）。
⑷反比例函数（）中比例系数的几何意义是：过双曲线 （）上任意引轴轴的垂线，所得矩形面积为。
4．反比例函数性质如下表：
的取值 图像所在象限 函数的增减性
一、三象限 在每个象限内，值随的增大而减小
二、四象限 在每个象限内，值随的增大而增大
5. 反比例函数解析式的确定：利用待定系数法（只需一对对应值或图像上一个点的坐标即可求出）
6．“反比例关系”与“反比例函数”：成反比例的关系式不一定是反比例函数,但是反比例函数中的两个变量必成反比例关系。
7. k的几何意义
　　如图1，设点P（a，b）是双曲线上任意一点，作PA⊥x轴于A点，PB⊥y轴于B点，则矩形PBOA的面积是（三角形PAO和三角形PBO的面积都是）．
　　如图2，由双曲线的对称性可知，P关于原点的对称点Q也在双曲线上，作QC⊥PA的延长线于C，则有三角形PQC的面积为．
　　 　　　　　　　　　　　　
　　 　　　　　　　　图1 　　　　　　　　　　　　　　　　　图2
　　说明：
　　（1）双曲线的两个分支是断开的，研究反比例函数的增减性时，要将两个分支分别讨论，不能一概而论．
　　（2）直线与双曲线的关系：
　　 　当时，两图象没有交点；当时，两图象必有两个交点，且这两个交点关于原点成中心对称．
　　（3）反比例函数与一次函数的联系．
二、例题
　1．反比例函数的概念
　　（1）下列函数中，y是x的反比例函数的是（ ）．
　　A．y=3x 　　　B．　　　　 C．3xy=1 　　　　D．
　　（2）下列函数中，y是x的反比例函数的是（ ）．
　　A．　　　　B．　　　　 C．　　　　D．
　　2．图象和性质
　　（1）已知函数是反比例函数，
　　①若它的图象在第二、四象限内，那么k=___________．
　　②若y随x的增大而减小，那么k=___________．
　　（2）已知一次函数y=ax+b的图象经过第一、二、四象限，则函数的图象位于第________象限．
　　（3）若反比例函数经过点（，2），则一次函数的图象一定不经过第_____象限．
　　（4）已知a·b＜0，点P（a，b）在反比例函数的图象上，
　　　　 则直线不经过的象限是（ ）．
　　A．第一象限 　　　　 B．第二象限　　　 C．第三象限　　　　　 D．第四象限
　　（5）若P（2，2）和Q（m，）是反比例函数图象上的两点，
　　　　 则一次函数y=kx+m的图象经过（ ）．
　　A．第一、二、三象限 　　　　　　B．第一、二、四象限
　　C．第一、三、四象限 　　　　　　D．第二、三、四象限
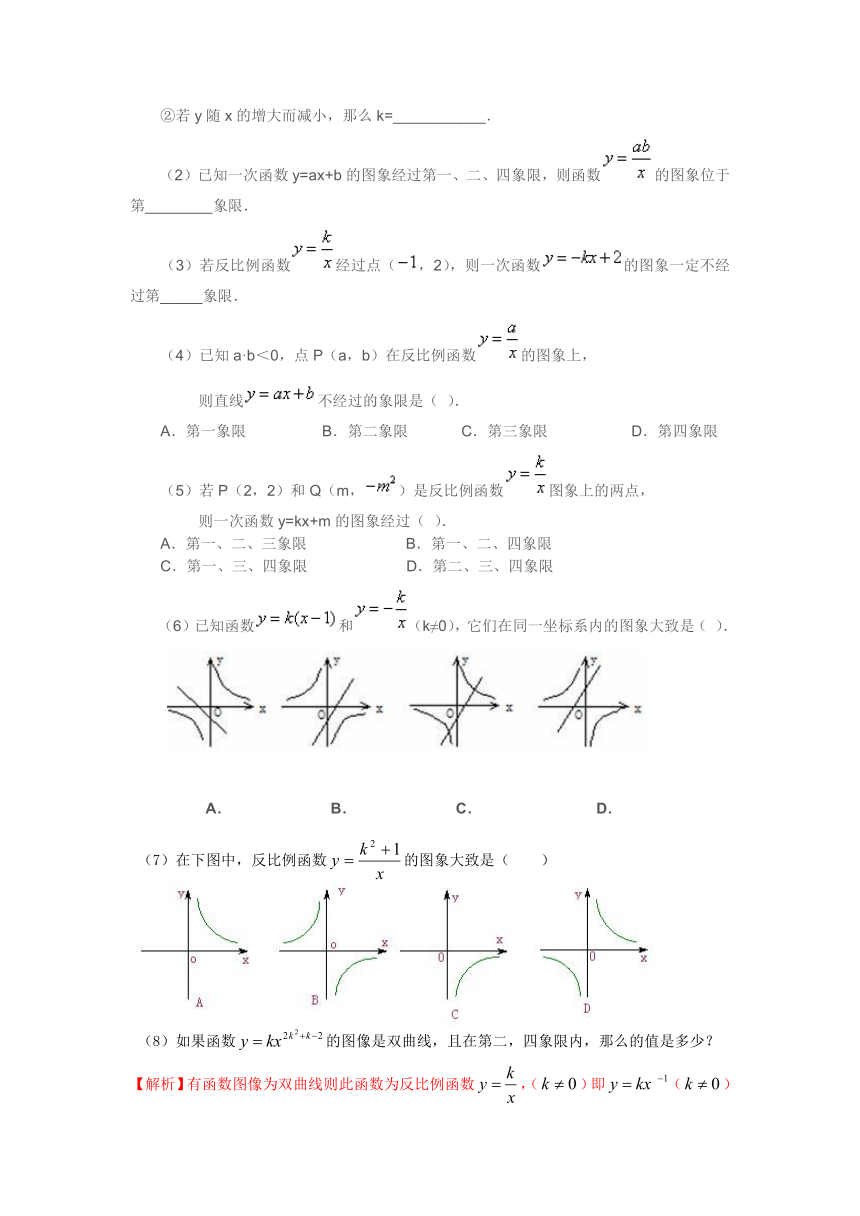
　　（6）已知函数和（k≠0），它们在同一坐标系内的图象大致是（ ）．
　　
　　 　　 A． 　　　　　　B．　　　　　　 C． 　　　　　　　D．
（7）在下图中，反比例函数的图象大致是（ ）
（8）如果函数的图像是双曲线，且在第二，四象限内，那么的值是多少？
【解析】有函数图像为双曲线则此函数为反比例函数，（）即（）又在第二，四象限内，则可以求出的值
【答案】由反比例函数的定义，得：
解得
时函数为
（9）如果一次函数相交于点（），那么该直线与双曲线的另一个交点为（ ）
【解析】
　
　　 3．函数的增减性
　　（1）在反比例函数的图象上有两点，，且，则的值为（ ）．
　　A．正数 　　　　B．负数　　　　　 C．非正数　　　　　 D．非负数
　　（2）在函数（a为常数）的图象上有三个点，，，则函数值、、的大小关系是（ ）．
　　A．＜＜　　　B．＜＜　　　　　C．＜＜　　　D．＜＜
　　（3）下列四个函数中：①；②；③；④．
　　　　 y随x的增大而减小的函数有（ ）．
　　A．0个　　　　 B．1个 　　　　　C．2个 　　　　　D．3个
　　（4）已知反比例函数的图象与直线y=2x和y=x+1的图象过同一点，则当x＞0时，这个反比例函数的函数值y随x的增大而　　　　（填“增大”或“减小”）．
（5）在反比例函数的图像上有三点，，，，， 。若则下列各式正确的是（ ）
A． B． C． D．
【解析】可直接以数的角度比较大小，也可用图像法，还可取特殊值法。
解法一：由题意得，，
，所以选A
解法二：用图像法，在直角坐标系中作出的图像
描出三个点，满足观察图像直接得到选A
解法三：用特殊值法
　注意，（3）中只有②是符合题意的，而③是在“每一个象限内” y随x的增大而减小．
　　4．解析式的确定
　　（1）若与成反比例，与成正比例，则y是z的（ ）．
　　A．正比例函数　　　 B．反比例函数 　　　　C．一次函数 　　　　D．不能确定
　　（2）若正比例函数y=2x与反比例函数的图象有一个交点为 （2，m），则m=_____，k=________，它们的另一个交点为________．
　　（3）已知反比例函数的图象经过点，反比例函数的图象在第二、四象限，求的值．
　5．面积计算
　　（1）如图，在函数的图象上有三个点A、B、C，过这三个点分别向x轴、y轴作垂线，过每一点所作的两条垂线段与x轴、y轴围成的矩形的面积分别为、、，则（ ）．
　　A．　　　　B．　　　　C．　　　　D．
　　 　　　　　　　　　　　　　　
　　 　第（1）题图 　　　　　　　　　　　　　　　　　　　第（2）题图
　　（2）如图，A、B是函数的图象上关于原点O对称的任意两点，AC//y轴，BC//x轴，△ABC的面积S，则（ ）．
　　A．S=1 　　　　B．1＜S＜2　　　　　　 C．S=2 　　　　　D．S＞2
　　（3）如图，Rt△AOB的顶点A在双曲线上，且S△AOB=3，求m的值．
　　 　　　　　　　　　　　　　
　　 　第（3）题图 　　　　　　　　　　　　　　　　　　第（4）题图
　　（4）已知函数的图象和两条直线y=x，y=2x在第一象限内分别相交于P1和P2两点，过P1分别作x轴、y轴的垂线P1Q1，P1R1，垂足分别为Q1，R1，过P2分别作x轴、y轴的垂线P2 Q 2，P2 R 2，垂足分别为Q 2，R 2，求矩形O Q 1P1 R 1和O Q 2P2 R 2的周长，并比较它们的大小．
　　
如图，正比例函数y=kx（k＞0）和反比例函数的图象相交于A、C两点，过A作x轴垂线交x轴于B，连接BC，若△ABC面积为S，则S=_________．
　　　　 　　　　　　　　　　　　　
　　 　　　第（5）题图 　　　　　　　　　　　　　　　　　　　第（6）题图
　　（6）如图在Rt△ABO中，顶点A是双曲线与直线在第四象限的交点，AB⊥x轴于B且S△ABO=．
　　①求这两个函数的解析式；
　　②求直线与双曲线的两个交点A、C的坐标和△AOC的面积．
　
（7）如图，在中，点是直线与双曲线在第一象限的交点，且，则的值是_____.
解:因为直线与双曲线过点,设点的坐标为.
则有.所以.
又点在第一象限,所以.
所以.而已知.
所以.
　　　6．综合应用
　　（1）若函数y=k1x（k1≠0）和函数（k2 ≠0）在同一坐标系内的图象没有公共点，则k1和k2（　　）．
　　A．互为倒数　　　 B．符号相同　　　 C．绝对值相等　　　 D．符号相反
　　
如图，一次函数的图象与反比例数的图象交于A、B两点：A（，1），B（1，n）．
　　① 求反比例函数和一次函数的解析式；
　　② 根据图象写出使一次函数的值大于反比例函数的值的x的取值范围．
（3）如图所示，已知一次函数（k≠0）的图象与x 轴、y轴分别交于A、B两点，且与反比例函数（m≠0）的图象在第一象限交于C点，CD垂直于x轴，垂足为D，若OA=OB=OD=1．
　　① 求点A、B、D的坐标；
　　② 求一次函数和反比例函数的解析式．
　 　
如图，一次函数的图象与反比例函数的图象交于第一象限C、D两点，坐标轴交于A、B两点，连结OC，OD（O是坐标原点）．
　　① 利用图中条件，求反比例函数的解析式和m的值；
　　② 双曲线上是否存在一点P，使得△POC和△POD的面积相等？若存在，给出证明并求出点P的坐标；若不存在，说明理由．
　　（5）不解方程，判断下列方程解的个数．
　　 　　①； 　　②．
　解析：①构造双曲线和直线，它们无交点，说明原方程无实数解；
　　　　 ②构造双曲线和直线，它们有两个交点，说明原方程有两个实数解．
三、练习题
1.反比例函数的图像位于（ ）
A．第一、二象限 B．第一、三象限 C．第二、三象限 D．第二、四象限
2.若与成反比例，与成正比例，则是的（ ）
A、正比例函数　　 B、反比例函数　　 C、一次函数　　D、不能确定
3.如果矩形的面积为6cm2，那么它的长cm与宽cm之间的函数图象大致为（ ）
4.某气球内充满了一定质量的气体，当温度不变时，
气球内气体的气压P ( kPa ) 是气体体积V ( m3 )
的反比例函数，其图象如图所示．当气球内气压大于120 kPa时，气球将爆炸．为了安全起见，气球的体积应（ ）
A、不小于m3 B、小于m3 C、不小于m3 D、小于m3
5．如图 ，A、C是函数的图象上的任意两点，过A作轴的垂线，垂足为B，过C作y轴的垂线，垂足为D，记RtΔAOB的面积为S1，RtΔCOD的面积为S2则 （ ）
S1 ＞S2 B． S1 C． S1=S2 D． S1与S2的大小关系不能确定
6．关于x的一次函数y=-2x+m和反比例函数y=的图象都经过点A（-2，1）.
求：（1）一次函数和反比例函数的解析式；（2）两函数图象的另一个交点B的坐标；
（3）△AOB的面积．
7. 如图所示，一次函数y＝ax＋b的图象与反比例函数y＝的图象交于A、B两点，与x轴交于点C．已知点A的坐标为（－2，1），点B的坐标为（，m）．
（1）求反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．
8． 某蓄水池的排水管每小时排水8m3，6小时可将满池水全部排空．
（1）蓄水池的容积是多少？
（2）如果增加排水管，使每小时的排水量达到Q（m3），那么将满池水排空所需的时间t（h）将如何变化？
（3）写出t与Q的关系式．
（4）如果准备在5小时内将满池水排空，那么每小时的排水量至少为多少？
（5）已知排水管的最大排水量为每小时12m3，那么最少需多长时间可将满池水全部排空？
9.某商场出售一批名牌衬衣，衬衣进价为60元，在营销中发现，该衬衣的日销售量y（件）是日销售价x元的反比例函数，且当售价定为100元/件时，每日可售出30件.
（1）请写出y关于x的函数关系式；
（2）该商场计划经营此种衬衣的日销售利润为1800元，则其售价应为多少元？
10．如图，在直角坐标系xOy中，一次函数y＝kx＋b的图象与反比例函数的图象交于A(-2，1)、B(1，n)两点。
(1)求上述反比例函数和一次函数的表达式；
(2)求△AOB的面积。
四、课后练习
1．对与反比例函数，下列说法不正确的是（ ）
A．点（）在它的图像上
B．它的图像在第一、三象限
C．当时，
D．当时，
2.已知反比例函数的图象经过点（1，-2），则这个函数的图象一定经过（　 ）
A、（2，1） B、（2，-1） C、（2，4） D、（-1，-2）
3．在同一直角坐标平面内，如果直线与双曲线没有交点，那么和的关系一定是（ ）
A. +=0 B. ·<0 C. ·>0 D.=
4. 如图,一次函数ｙ=x－1与反比例函数ｙ=的图像交于点A(2,1),B(－1,－2),
则使ｙ＞ｙ的ｘ的取值范围是( )
A. ｘ＞2 B. ｘ＞2 或－1＜ｘ＜0
C. －1＜ｘ＜2 D. ｘ＞2 或ｘ＜－1
5. 点P（2m－3，1）在反比例函数y＝的图象上，则m＝__________．
6. 已知反比例函数的图象经过点（m，2）和（－2，3）则m的值为__________．
7.函数与在同一坐标系内的图象可以是（ ）
8.反比例函数与二次函数在同一平面直角坐标系中的大致图象如图所示，
它们的解析式可能分别是（ ）．
A. y=，y=kx2-x B. y=，y=kx2+x C. y=-，y=kx2+x D. y=-，y=-kx2-x
9. 已知反比例函数的图象上两点，当时，有，则的取值范围是？
10.如图，反比例函数的图象与直线相交于B两点，AC∥轴，
BC∥轴，则△ABC的面积等于 个面积单位.　
11. 已知,且反比例函数的图象在每个象限内，随的增大而增大,如果点在双曲线上，求a是多少？
12. 如图14，已知 HYPERLINK "http://www." ，是一次函数的图象和反比例函数的图象的两个交点．
(1)求反比例函数和一次函数的解析式；
(2)求直线与轴的交点的坐标及△的面积；
(3)求方程的解（请直接写出答案）；
(4)求不等式的解集（请直接写出答案）.
13. 函数的图象如图所示，则结论：
①两函数图象的交点的坐标为；
②当时，；
③当时，；
④当逐渐增大时，随着的增大而增大，随着的增大而减小．
其中正确结论的序号是 ．
14. 如图，⊙A和⊙B都与x轴和y轴相切，圆心A和圆心B都在反比例函数的图象上，则图中阴影部分的面积等于 .
o
y
x
y
x
o
y
x
o
y
x
o
A B C D
O
B
ｙ
ｘ
AAA
x
y
O
A．
x
y
O
B．
x
y
O
C．
x
y
O
D．
O
x
y
C
B
A
O
O
x
A
B
C
y