浙教版八年级上册数学每日一题16-20(第2章 特殊三角形)培优训练(含详解)
文档属性
| 名称 | 浙教版八年级上册数学每日一题16-20(第2章 特殊三角形)培优训练(含详解) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 15:42:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
每日一题16
班级 姓名 小组
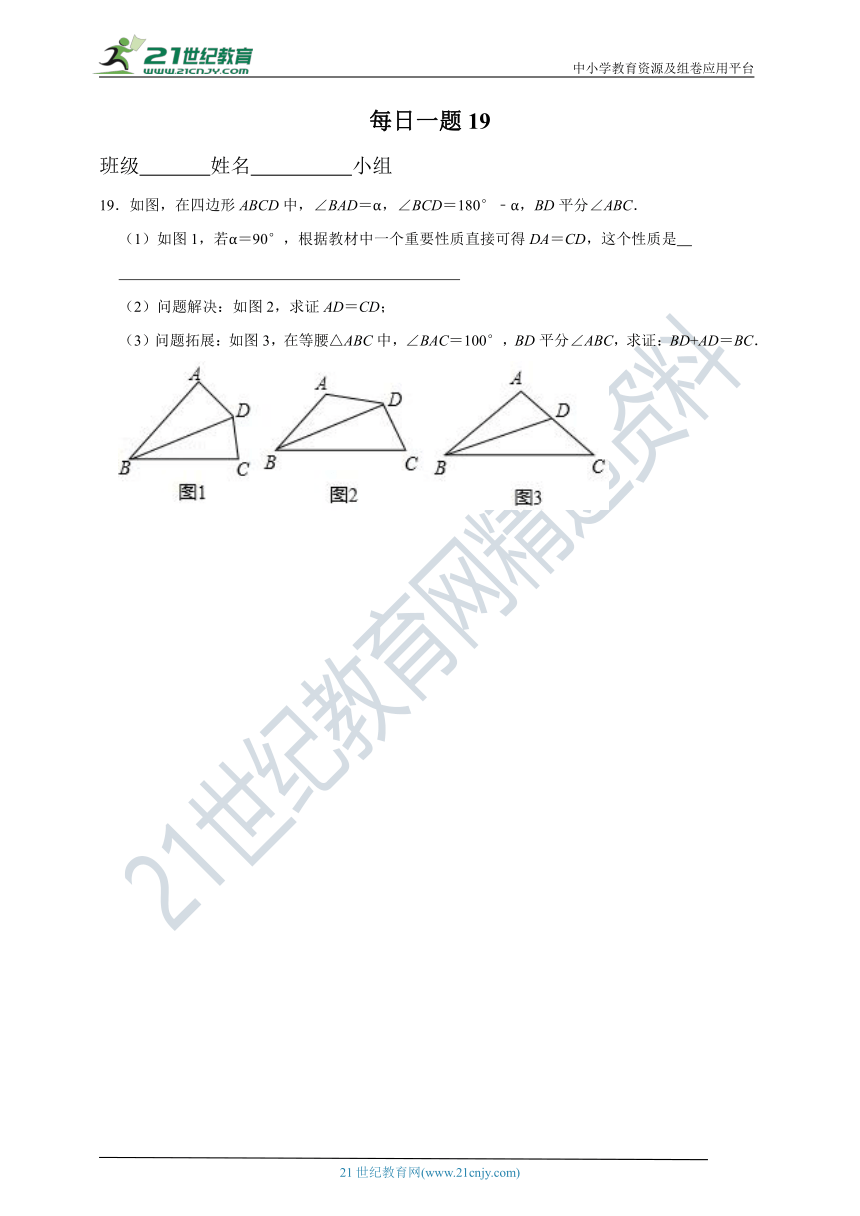
16.在Rt△ABC中,∠B=90°,AB=2,BC=4,AC的中垂线DE交AC于D,交BC于点E.
(1)如图1,连接AE,则AE= ;
(2)如图2,延长DE交AB的延长线于点F,连接CF,请求出CF的长;
(3)如图3,点P为直线DE上一动点,点Q为直线AB上一动点,则BP+PQ的最小值为 .
每日一题17
班级 姓名 小组
17.在△ABC中,AB=AC.
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?
请用式子表示:
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.
每日一题18
班级 姓名 小组
18.已知,在△ABC中,∠ABC=∠ACB,点D为射线CB上一点,过点D作DE⊥AC于点E.
(1)如图1,当点D在线段BC上时,请直接写出∠BAC与∠EDC的数量关系: .
(2)如图2,当点D在CB的延长线上时,画出图形,探究∠BAC与∠EDC的数量关系,并说明理由.
(3)在(2)的条件下,点F为线段BC上一点,过点F作FG⊥AC于点G,连接AF,且∠AFG=∠CFG,∠BAF=∠BFA,延长ED、AB交于点K,求∠EKA的度数.
每日一题19
班级 姓名 小组
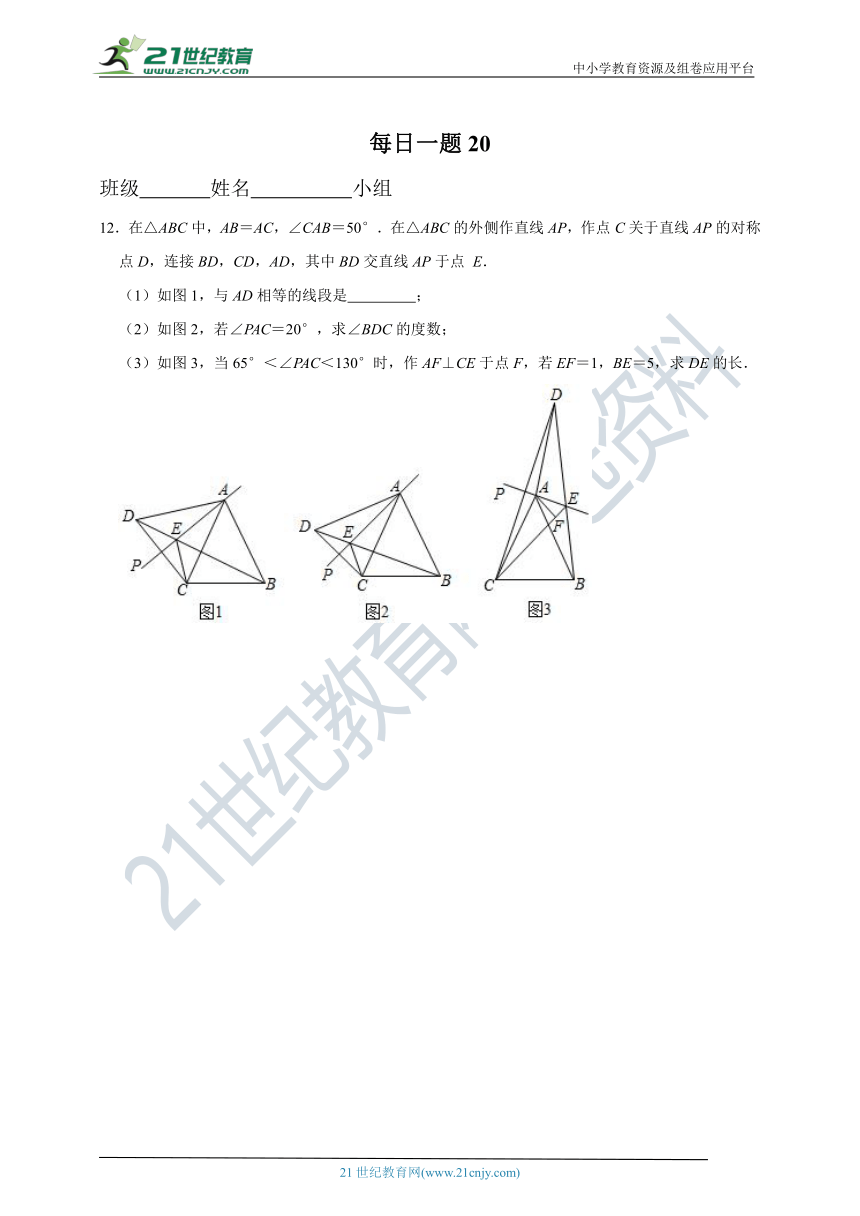
19.如图,在四边形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
(1)如图1,若α=90°,根据教材中一个重要性质直接可得DA=CD,这个性质是
(2)问题解决:如图2,求证AD=CD;
(3)问题拓展:如图3,在等腰△ABC中,∠BAC=100°,BD平分∠ABC,求证:BD+AD=BC.
每日一题20
班级 姓名 小组
12.在△ABC中,AB=AC,∠CAB=50°.在△ABC的外侧作直线AP,作点C关于直线AP的对称点D,连接BD,CD,AD,其中BD交直线AP于点 E.
(1)如图1,与AD相等的线段是 ;
(2)如图2,若∠PAC=20°,求∠BDC的度数;
(3)如图3,当65°<∠PAC<130°时,作AF⊥CE于点F,若EF=1,BE=5,求DE的长.
每日一题16 参考答案
16.【解答】解:(1)∵DE是AC的中垂线,∴AE=CE,
设AE=CE=x,则BE=BC﹣CE=4﹣x,
在Rt△ABE中,由勾股定理得:22+(4﹣x)2=x2,
解得:x=,即AE=,故答案为:;
(2)∵DE是AC的中垂线,∴AF=CF,
设AF=CF=y,则BF=y﹣2,在Rt△BCF中,由勾股定理得:(y﹣2)2+42=y2,
解得:y=5,即CF的长为5;
(3)方法一:连接CF,过B作BM⊥CF于M,交直线DE于P',过P'作P'Q'⊥BF于Q',如图3所示:∵DE是AC的中垂线,∴AF=CF,∴∠AFD=∠CFD,
∵P'M⊥CF,P'Q'⊥BF,∴P'M=P'Q',
则点M与Q'关于DE对称,此时BM=BP'+P'M=BP'+P'Q',即BP+PQ的值最小=BM,
由(2)得:AF=CF=5,AB=2,∴BF=AF﹣AB=3,
∵∠CBF=180°﹣∠ABC=90°,∴△BCF的面积=CF×BM=BF×BC
∴BM===,即BP+PQ的最小值为,故答案为:.
方法二:
作点B关于DE的对称点H,交DF于G,过点H作HQ⊥AB于Q,交DE于点P,如图4所示:
则点P、Q就是使BP+PQ最小的点,
由对称得:∠AFD=∠CFD,∠AFD=∠HFD,BP=HP,FB=FH,
∴∠CFD=∠HFD,
∴点C、H、F三点共线.BP+PQ=HP+PQ=HQ,
由“垂线段最短”得:BP+PQ的最小值为HQ.
在等腰△BFH中,∵FB=FH,HQ⊥BF过B作BM⊥CF于M,
∴HQ=BM(等腰三角形两腰上的高相等).
由方法一得:BM=.
∴BP+PQ的最小值为.故答案为:.
每日一题17 参考答案
17.解:(1)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=30°,
∴∠BAD=∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠EDC=15°.
(2)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=40°,
∴∠BAD=∠CAD=40°,
∵AD=AE,
∴∠ADE=∠AED=70°,
∴∠EDC=20°.
(3)∠BAD=2∠EDC(或∠EDC=∠BAD)
(4)仍成立,理由如下
∵AD=AE,∴∠ADE=∠AED,
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=(∠EDC+∠C)+∠EDC
=2∠EDC+∠C
又∵AB=AC,
∴∠B=∠C
∴∠BAD=2∠EDC.
故分别填15°,20°,∠EDC=∠BAD
每日一题18 参考答案
18.(1)如图1中,作AH⊥BC于H.
∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH,
∵DE⊥AC,
∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.
故答案为∠BAC=2∠EDC.
(2)如图2中,结论:∠BAC=2∠EDC.
理由:∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH,
∵DE⊥AC,
∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.
(3)如图2中,设∠C=∠FAC=∠ABC=x,则∠BAF=∠BFA=2x,
∴5x=180°,
∴x=36°,
∴∠EAK=∠ABC+∠C=72°,
∵KE⊥EC,
∴∠E=90°,
∴∠EKA=90°﹣72°=18°.
每日一题19 参考答案
19.解:(1)∵BD平分∠ABC,∠BAD=90°,∠BCD=90°,
∴DA=DC(角平分线上的点到角的两边距离相等),
故答案为:角平分线上的点到角的两边距离相等;
(2)如图2,作DE⊥BA交BA延长线于E,DF⊥BC于F,
∵BD平分∠EBF,DE⊥BE,DF⊥BF,
∴DE=DF,
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,
∴∠EAD=∠C,
在△DEA和△DFC中,
∴△DEA≌△DFC(AAS),
∴DA=DC;
(3)如图3,在BC时截取BK=BD,连接DK,
∵AB=AC,∠A=100°,
∴∠ABC=∠C=40°,
∵BD平分∠ABC,
∴∠DBK=∠ABC=20°,
∵BD=BK,
∴∠BKD=∠BDK=80°,即∠A+∠BKD=180°,
由(2)的结论得AD=DK,
∵∠BKD=∠C+∠KDC,
∴∠KDC=∠C=40°,
∴DK=CK,
∴AD=DK=CK,
∴BD+AD=BK+CK=BC.
每日一题20 参考答案
20.解:(1)如图 1,∵点C关于直线AP的对称点D,
∴AD=AC,
∵AC=AB,
∴AD=AC=AB,
∴与 AD 相等的线段是AC,AB;
故答案为:AC,AB;
(2)∵点 C 与点 D 关于直线 AP 对称,
∴AD=AC,∠DAP=∠CAP=20°
∴∠DAC=40°,∠ADC=70°,
又∵∠CAB=50°,
∴∠DAB=90°,
∵AC=AB,
∴AD=AB,
∴∠ADB=45°,
∴∠BDC=∠ADC﹣∠ADB=25°;
(3)在 CE 上截取 GF=EF,连接 AG
∵点 C 与点 D 关于直线 AP 对称
∴AD=AC,∠ADE=∠ACE
∵AD=AC=AB,
∴∠ADB=∠ABD,
∴∠ACE=∠ABD,
∵AF⊥CE,GF=EF,
∴AG=AE,
∴∠AGE=∠AEG,
∵∠AED=∠AEG,
∴∠AGE=∠AED,
∴∠AGC=∠AEB,
在△ACG 和△ABE 中,,
∴△ACG≌△ABE(AAS),
∴BE=CG,
∵BE=5,EF=1,
∴DE=CE=CG+2EF=BE+2EF=7.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题16
班级 姓名 小组
16.在Rt△ABC中,∠B=90°,AB=2,BC=4,AC的中垂线DE交AC于D,交BC于点E.
(1)如图1,连接AE,则AE= ;
(2)如图2,延长DE交AB的延长线于点F,连接CF,请求出CF的长;
(3)如图3,点P为直线DE上一动点,点Q为直线AB上一动点,则BP+PQ的最小值为 .
每日一题17
班级 姓名 小组
17.在△ABC中,AB=AC.
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?
请用式子表示:
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.
每日一题18
班级 姓名 小组
18.已知,在△ABC中,∠ABC=∠ACB,点D为射线CB上一点,过点D作DE⊥AC于点E.
(1)如图1,当点D在线段BC上时,请直接写出∠BAC与∠EDC的数量关系: .
(2)如图2,当点D在CB的延长线上时,画出图形,探究∠BAC与∠EDC的数量关系,并说明理由.
(3)在(2)的条件下,点F为线段BC上一点,过点F作FG⊥AC于点G,连接AF,且∠AFG=∠CFG,∠BAF=∠BFA,延长ED、AB交于点K,求∠EKA的度数.
每日一题19
班级 姓名 小组
19.如图,在四边形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
(1)如图1,若α=90°,根据教材中一个重要性质直接可得DA=CD,这个性质是
(2)问题解决:如图2,求证AD=CD;
(3)问题拓展:如图3,在等腰△ABC中,∠BAC=100°,BD平分∠ABC,求证:BD+AD=BC.
每日一题20
班级 姓名 小组
12.在△ABC中,AB=AC,∠CAB=50°.在△ABC的外侧作直线AP,作点C关于直线AP的对称点D,连接BD,CD,AD,其中BD交直线AP于点 E.
(1)如图1,与AD相等的线段是 ;
(2)如图2,若∠PAC=20°,求∠BDC的度数;
(3)如图3,当65°<∠PAC<130°时,作AF⊥CE于点F,若EF=1,BE=5,求DE的长.
每日一题16 参考答案
16.【解答】解:(1)∵DE是AC的中垂线,∴AE=CE,
设AE=CE=x,则BE=BC﹣CE=4﹣x,
在Rt△ABE中,由勾股定理得:22+(4﹣x)2=x2,
解得:x=,即AE=,故答案为:;
(2)∵DE是AC的中垂线,∴AF=CF,
设AF=CF=y,则BF=y﹣2,在Rt△BCF中,由勾股定理得:(y﹣2)2+42=y2,
解得:y=5,即CF的长为5;
(3)方法一:连接CF,过B作BM⊥CF于M,交直线DE于P',过P'作P'Q'⊥BF于Q',如图3所示:∵DE是AC的中垂线,∴AF=CF,∴∠AFD=∠CFD,
∵P'M⊥CF,P'Q'⊥BF,∴P'M=P'Q',
则点M与Q'关于DE对称,此时BM=BP'+P'M=BP'+P'Q',即BP+PQ的值最小=BM,
由(2)得:AF=CF=5,AB=2,∴BF=AF﹣AB=3,
∵∠CBF=180°﹣∠ABC=90°,∴△BCF的面积=CF×BM=BF×BC
∴BM===,即BP+PQ的最小值为,故答案为:.
方法二:
作点B关于DE的对称点H,交DF于G,过点H作HQ⊥AB于Q,交DE于点P,如图4所示:
则点P、Q就是使BP+PQ最小的点,
由对称得:∠AFD=∠CFD,∠AFD=∠HFD,BP=HP,FB=FH,
∴∠CFD=∠HFD,
∴点C、H、F三点共线.BP+PQ=HP+PQ=HQ,
由“垂线段最短”得:BP+PQ的最小值为HQ.
在等腰△BFH中,∵FB=FH,HQ⊥BF过B作BM⊥CF于M,
∴HQ=BM(等腰三角形两腰上的高相等).
由方法一得:BM=.
∴BP+PQ的最小值为.故答案为:.
每日一题17 参考答案
17.解:(1)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=30°,
∴∠BAD=∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠EDC=15°.
(2)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=40°,
∴∠BAD=∠CAD=40°,
∵AD=AE,
∴∠ADE=∠AED=70°,
∴∠EDC=20°.
(3)∠BAD=2∠EDC(或∠EDC=∠BAD)
(4)仍成立,理由如下
∵AD=AE,∴∠ADE=∠AED,
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=(∠EDC+∠C)+∠EDC
=2∠EDC+∠C
又∵AB=AC,
∴∠B=∠C
∴∠BAD=2∠EDC.
故分别填15°,20°,∠EDC=∠BAD
每日一题18 参考答案
18.(1)如图1中,作AH⊥BC于H.
∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH,
∵DE⊥AC,
∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.
故答案为∠BAC=2∠EDC.
(2)如图2中,结论:∠BAC=2∠EDC.
理由:∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH,
∵DE⊥AC,
∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.
(3)如图2中,设∠C=∠FAC=∠ABC=x,则∠BAF=∠BFA=2x,
∴5x=180°,
∴x=36°,
∴∠EAK=∠ABC+∠C=72°,
∵KE⊥EC,
∴∠E=90°,
∴∠EKA=90°﹣72°=18°.
每日一题19 参考答案
19.解:(1)∵BD平分∠ABC,∠BAD=90°,∠BCD=90°,
∴DA=DC(角平分线上的点到角的两边距离相等),
故答案为:角平分线上的点到角的两边距离相等;
(2)如图2,作DE⊥BA交BA延长线于E,DF⊥BC于F,
∵BD平分∠EBF,DE⊥BE,DF⊥BF,
∴DE=DF,
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,
∴∠EAD=∠C,
在△DEA和△DFC中,
∴△DEA≌△DFC(AAS),
∴DA=DC;
(3)如图3,在BC时截取BK=BD,连接DK,
∵AB=AC,∠A=100°,
∴∠ABC=∠C=40°,
∵BD平分∠ABC,
∴∠DBK=∠ABC=20°,
∵BD=BK,
∴∠BKD=∠BDK=80°,即∠A+∠BKD=180°,
由(2)的结论得AD=DK,
∵∠BKD=∠C+∠KDC,
∴∠KDC=∠C=40°,
∴DK=CK,
∴AD=DK=CK,
∴BD+AD=BK+CK=BC.
每日一题20 参考答案
20.解:(1)如图 1,∵点C关于直线AP的对称点D,
∴AD=AC,
∵AC=AB,
∴AD=AC=AB,
∴与 AD 相等的线段是AC,AB;
故答案为:AC,AB;
(2)∵点 C 与点 D 关于直线 AP 对称,
∴AD=AC,∠DAP=∠CAP=20°
∴∠DAC=40°,∠ADC=70°,
又∵∠CAB=50°,
∴∠DAB=90°,
∵AC=AB,
∴AD=AB,
∴∠ADB=45°,
∴∠BDC=∠ADC﹣∠ADB=25°;
(3)在 CE 上截取 GF=EF,连接 AG
∵点 C 与点 D 关于直线 AP 对称
∴AD=AC,∠ADE=∠ACE
∵AD=AC=AB,
∴∠ADB=∠ABD,
∴∠ACE=∠ABD,
∵AF⊥CE,GF=EF,
∴AG=AE,
∴∠AGE=∠AEG,
∵∠AED=∠AEG,
∴∠AGE=∠AED,
∴∠AGC=∠AEB,
在△ACG 和△ABE 中,,
∴△ACG≌△ABE(AAS),
∴BE=CG,
∵BE=5,EF=1,
∴DE=CE=CG+2EF=BE+2EF=7.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
