浙教版八年级上册数学每日一题21-25(第2章 特殊三角形)培优练习(含答案)
文档属性
| 名称 | 浙教版八年级上册数学每日一题21-25(第2章 特殊三角形)培优练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 16:11:05 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
每日一题21
班级 姓名 小组
21.在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5
①求证:AF⊥BD②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD;
(3)如图3,在(2)的条件下,连接CF并延长CF交AD于点G,∠AFG是一个固定的值吗?若是,求出∠AFG的度数;若不是,请说明理由.
每日一题22
班级 姓名 小组
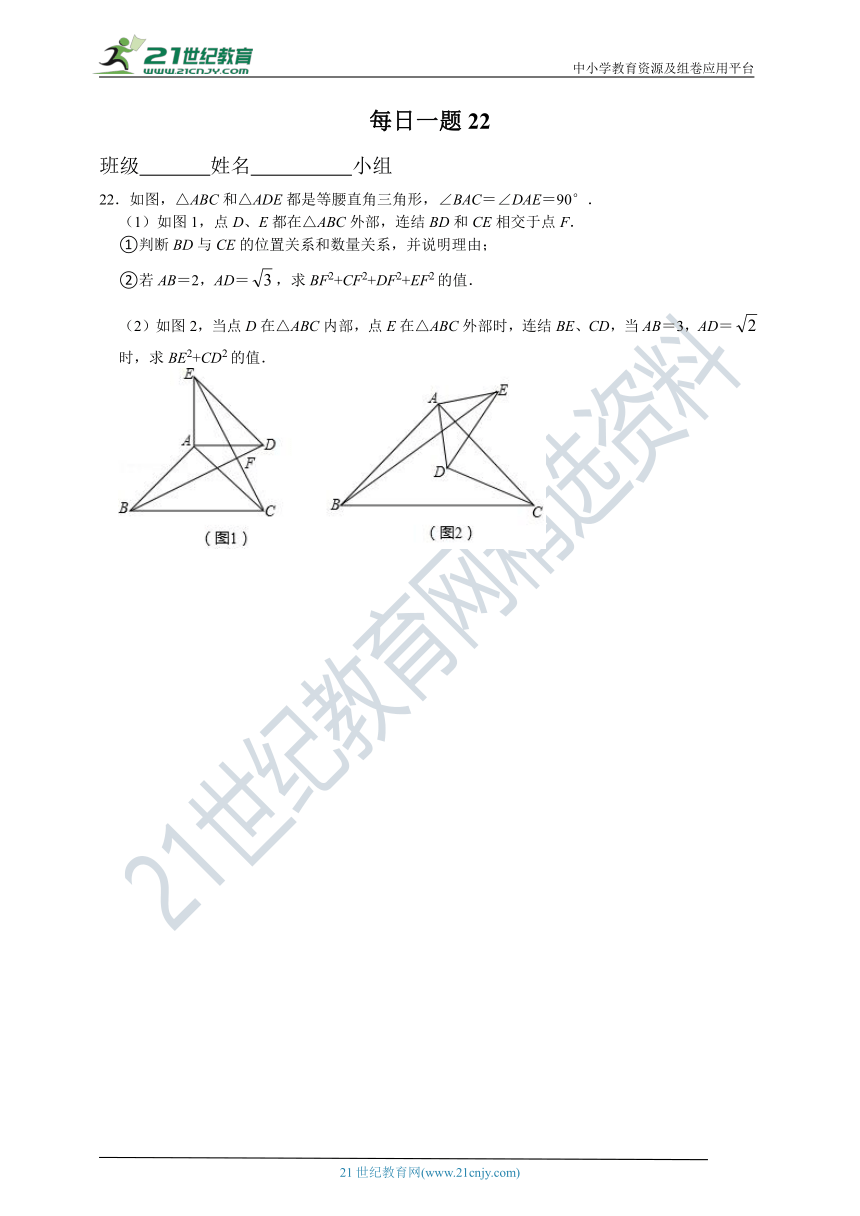
22.如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°.
(1)如图1,点D、E都在△ABC外部,连结BD和CE相交于点F.
①判断BD与CE的位置关系和数量关系,并说明理由;
②若AB=2,AD=,求BF2+CF2+DF2+EF2的值.
(2)如图2,当点D在△ABC内部,点E在△ABC外部时,连结BE、CD,当AB=3,AD=时,求BE2+CD2的值.
每日一题23
班级 姓名 小组
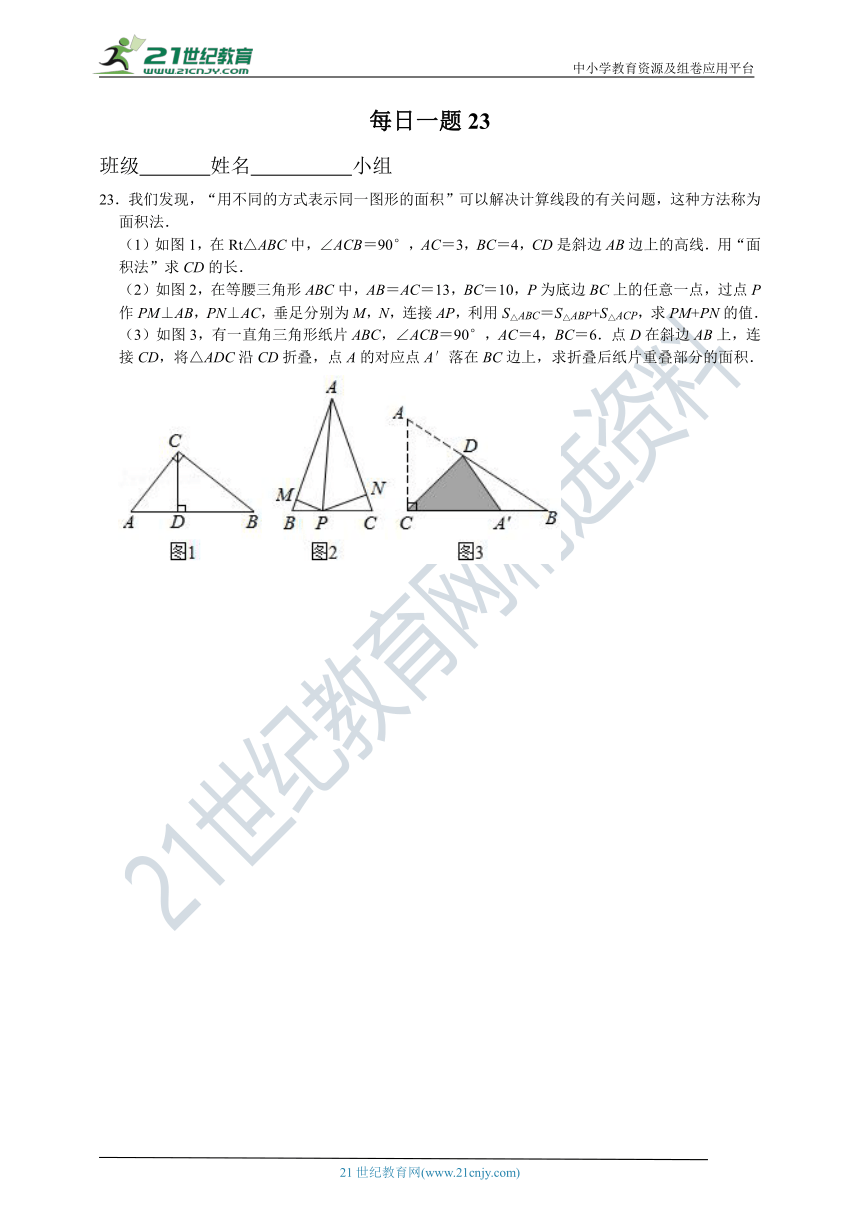
23.我们发现,“用不同的方式表示同一图形的面积”可以解决计算线段的有关问题,这种方法称为面积法.
(1)如图1,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD是斜边AB边上的高线.用“面积法”求CD的长.
(2)如图2,在等腰三角形ABC中,AB=AC=13,BC=10,P为底边BC上的任意一点,过点P作PM⊥AB,PN⊥AC,垂足分别为M,N,连接AP,利用S△ABC=S△ABP+S△ACP,求PM+PN的值.
(3)如图3,有一直角三角形纸片ABC,∠ACB=90°,AC=4,BC=6.点D在斜边AB上,连接CD,将△ADC沿CD折叠,点A的对应点A′落在BC边上,求折叠后纸片重叠部分的面积.
每日一题24
班级 姓名 小组
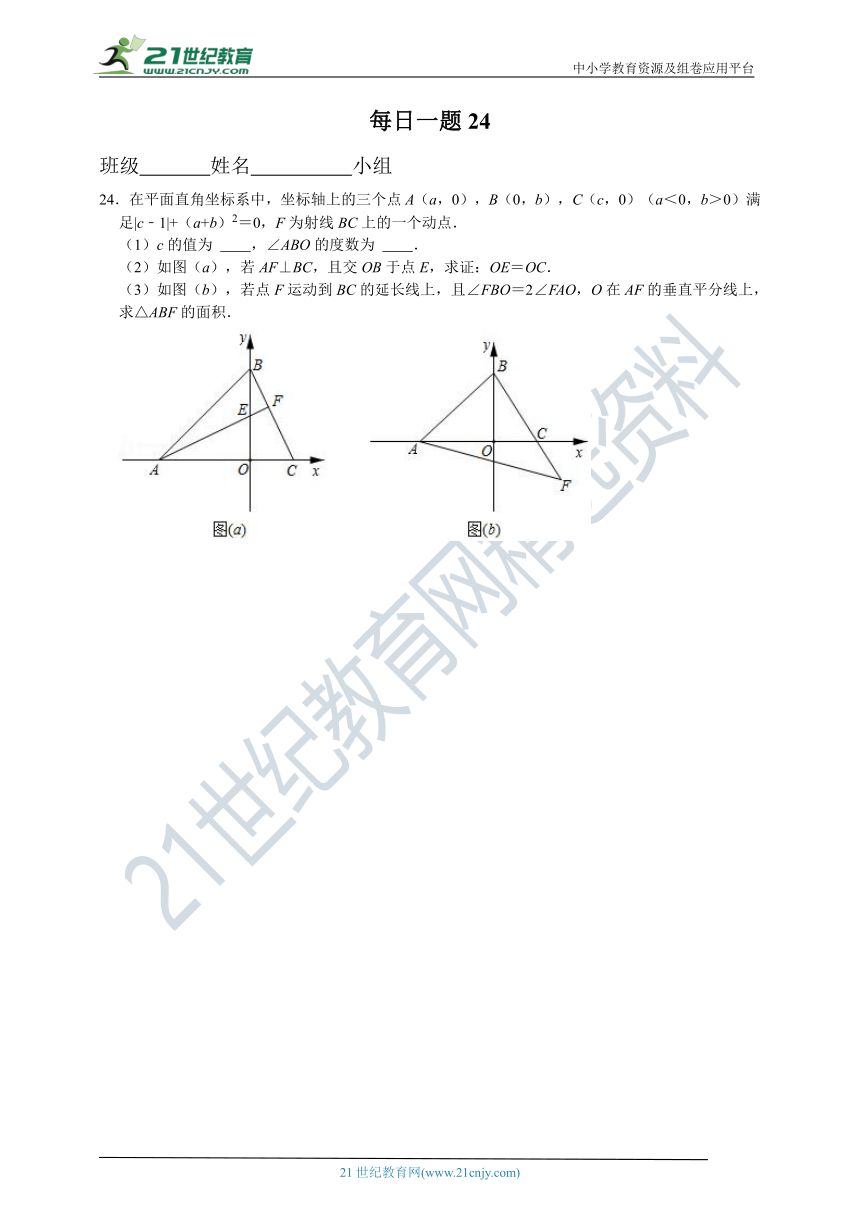
24.在平面直角坐标系中,坐标轴上的三个点A(a,0),B(0,b),C(c,0)(a<0,b>0)满足|c﹣1|+(a+b)2=0,F为射线BC上的一个动点.
(1)c的值为 ,∠ABO的度数为 .
(2)如图(a),若AF⊥BC,且交OB于点E,求证:OE=OC.
(3)如图(b),若点F运动到BC的延长线上,且∠FBO=2∠FAO,O在AF的垂直平分线上,求△ABF的面积.
每日一题25
班级 姓名 小组
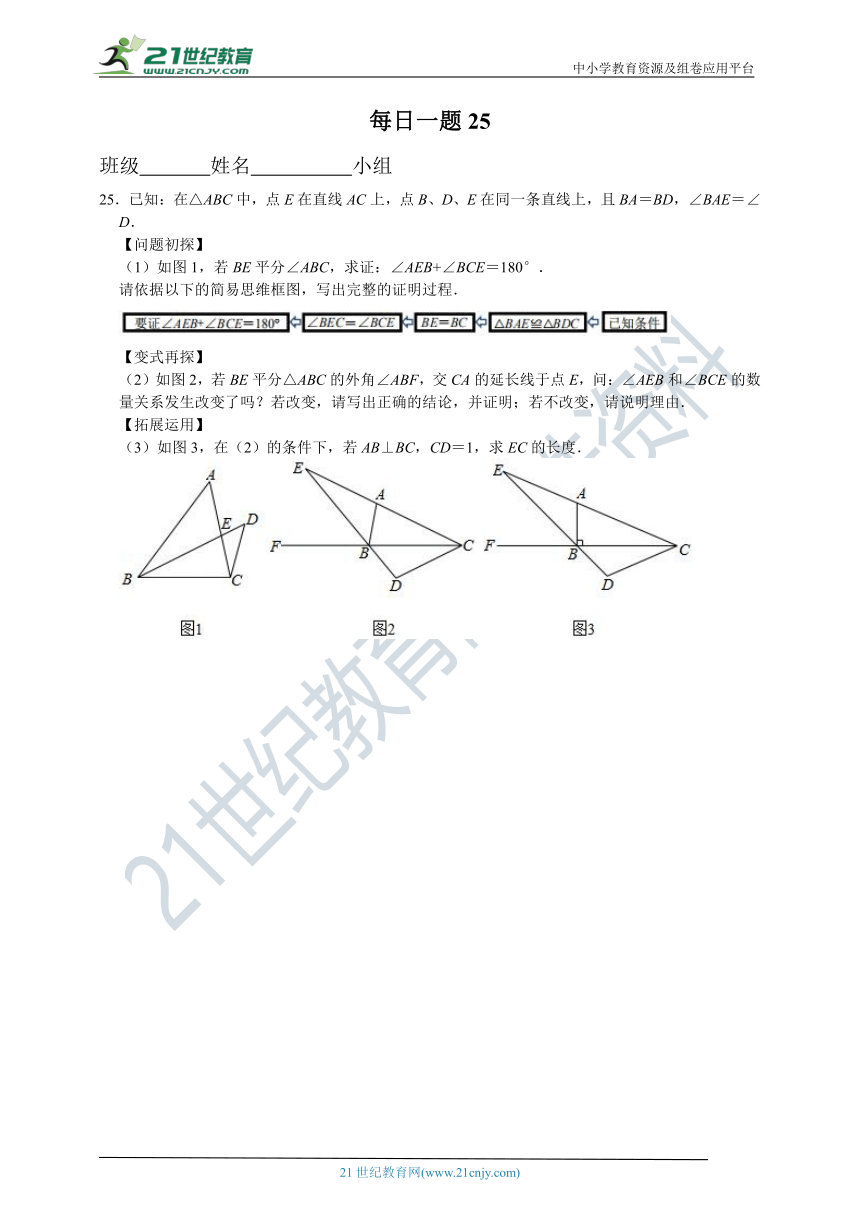
25.已知:在△ABC中,点E在直线AC上,点B、D、E在同一条直线上,且BA=BD,∠BAE=∠D.
【问题初探】
(1)如图1,若BE平分∠ABC,求证:∠AEB+∠BCE=180°.
请依据以下的简易思维框图,写出完整的证明过程.
【变式再探】
(2)如图2,若BE平分△ABC的外角∠ABF,交CA的延长线于点E,问:∠AEB和∠BCE的数量关系发生改变了吗?若改变,请写出正确的结论,并证明;若不改变,请说明理由.
【拓展运用】
(3)如图3,在(2)的条件下,若AB⊥BC,CD=1,求EC的长度.
每日一题21 参考答案
21.(1)①证明:如图1,
在△ACE和△BCD中,
∵,
∴△ACE≌△BCD,∴∠1=∠2,
∵∠3=∠4,∴∠BFE=∠ACE=90°,∴AF⊥BD.
②∵∠ECD=90°,BC=AC=12,DC=EC=5,
∴BD==13,
∵S△ABD=AD BC=BD AF,即
∴AF=.
(2)证明:如图4,
∵∠ACB=∠ECD,∴∠ACB+∠ACD=∠ECD+∠ACD,
∴∠BCD=∠ACE,
在△ACE≌△BCD中
∴△ACE≌△BCD,∴∠1=∠2,
∵∠3=∠4,∴∠BFA=∠BCA=90°,
∴AF⊥BD.
(3)∠AFG=45°,
如图3,过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,
∵△ACE≌△BCD,
∴S△ACE=S△BCD,AE=BD,
∵S△ACE=AE CN,
S△BCD=BD CM,
∴CM=CN,
∵CM⊥BD,CN⊥AE,
∴CF平分∠BFE,
∵AF⊥BD,
∴∠BFE=90°,
∴∠EFC=45°,
∴∠AFG=45°.
每日一题22 参考答案
22.解:(1)①BD=CE,BD⊥CE,理由如下:
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC+∠DAC,∠CAE=∠DAE+∠DAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠ABD+∠DBC=90°,
∴∠DBC+∠ACE=90°,
∴∠BFC=90°,即BD⊥CE;
②∵BD⊥CE,
∴∠BCF=∠EFD=90°,
∴BF2+CF2=BC2,DF2+EF2=DE2,
∴BF2+CF2+DF2+EF2=BC2+DE2,
∵△ABC和△ADE都是等腰直角三角形,
∴BC2=2AB2,DE2=2AD2,
∵AB=2,AD=,
∴BC2=2×22=8,=6,
∴BF2+CF2+DF2+EF2=8+6=14;
(2)连接CE,延长BD交AC于点O,交CE于点F,
同(1)可得△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠AOB=∠COF,
∴∠BAC=∠BFC=90°,
∴BD⊥CE,
∴BE2=BF2+EF2,CD2=CF2+DF2,
∴BE2+CD2=BF2+EF2+CF2+DF2,
∵BF2+CF2=BC2,DF2+EF2=DE2,
∴BE2+CD2=BC2+DE2,
∵AB=3,AD=,
∴DE=AD=2,BC=AB=3,
∴BE2+CD2==22.
每日一题23 参考答案
解:(1)如图1中,
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵CD⊥AB,
∴S△ABC= AC BC= AB CD,
∴CD==.
(2)如图2中,过点A作AH⊥BC于H.
∵AB=AC=13,BC=10,
∴BH=CH=5,
∴AH===12,
∵S△ABC= BC AH= AB PM+ AC PN,
∴×13×PM+×13×PN=×10×12,
∴PM+PN=.
(3)如图,过点D作DM⊥AC于M,DN⊥EC于N.
∵∠ACD=∠BCD,DM⊥AC,DN⊥CE,
∴DM=DN,
∵S△ACD+S△BCD=S△ACB,
∴×4×DM+×6×DN=×4×6,
∴DM=DN=,
∴S△A′CD= CA′ DN=×4×=.
每日一题24 参考答案
【解答】(1)解:∵|c﹣1|+(a+b)2=0,
∴c=1,a=﹣b,∴OA=OB,∴∠ABO=45°,
故答案为:1,45°.
(2)∵AF⊥BC,∴∠AOE=∠BFE=90°,
∵∠AEO=∠BEF,∴∠OBC=∠OAE,
在△AOE和△BOC中,
,
∴△AOE≌△BOC(AAS),
∴OE=OC;
(3)连结OF,过点F作FG⊥x轴,垂足为点G,
设∠FAO=x,则∠FBO=2∠FAO=2x,
∵O在AF的垂直平分线上,
∴AO=OF,
∴∠OAF=∠OFA=x,
∴∠GOF=∠OAF+∠OFA=2x,
∵∠FBO=2∠FAO=2x,OB=OA=OF,
∴∠OFC=∠OBF=2x,
∴∠BCO=∠COF+∠OFB=4x,
∵∠OBC+∠OCB=90°,
∴6x=90°,解得x=15°,
∴∠OBC=∠GOF=2x=30°,
∵C(1,0),
∴OC=1,
∵∠BOC=90°,∠OBC=30°,
∴BC=2OC=2,,
∴OA=OF=OB=,
同理可得:,
∴,
∴S△ABF=S△ACB+S△ACF=×AC×FG+×AC×OB=×(+1)(+)=+.
每日一题25 参考答案
证明:(1)∵BE平分∠ABC,
∴∠ABD=∠DBC,
又∵BA=BD,∠BAE=∠D,
∴△ABE≌△DBC(ASA),
∴BE=BC,
∴∠BCE=∠BEC,
∵∠AEB+∠BEC=180°,
∴∠AEB+∠BCE=180°;
(2)结论改变了,∠AEB=∠BCE,
理由如下:
∵BE平分∠ABF,
∴∠ABE=∠FBE=∠DBC,
又∵BA=BD,∠BAE=∠D,
∴△ABE≌△DBC(ASA),
∴∠AEB=∠BCE;
(3)如图3,连接AD,
∵AB⊥BC,
∴∠ABF=90°=∠ABC,
∴∠ABE=∠FBE=∠DBC=45°,
∵△ABE≌△DBC,
∴CD=AE=1,BE=BC,
∵AB=DB,∠ABD=∠ABC+∠CBD=135°,
∴∠BAD=∠BDA=22.5°,
∵BE=BC,
∴∠BEA=∠BCE,
∵∠EBF=∠E+∠BCE=45°,∠AEB=∠BCD,
∴∠BCD+∠BCE=45°=∠ACD,∠BEA=∠BCE=22.5°,
∴∠AEB=∠ADB=22.5°,
∴AE=AD=1,∠DAC=45°,
∴∠ADC=90°,
∴AC=CD=,
∴CE=AC+AE=+1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题21
班级 姓名 小组
21.在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5
①求证:AF⊥BD②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD;
(3)如图3,在(2)的条件下,连接CF并延长CF交AD于点G,∠AFG是一个固定的值吗?若是,求出∠AFG的度数;若不是,请说明理由.
每日一题22
班级 姓名 小组
22.如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°.
(1)如图1,点D、E都在△ABC外部,连结BD和CE相交于点F.
①判断BD与CE的位置关系和数量关系,并说明理由;
②若AB=2,AD=,求BF2+CF2+DF2+EF2的值.
(2)如图2,当点D在△ABC内部,点E在△ABC外部时,连结BE、CD,当AB=3,AD=时,求BE2+CD2的值.
每日一题23
班级 姓名 小组
23.我们发现,“用不同的方式表示同一图形的面积”可以解决计算线段的有关问题,这种方法称为面积法.
(1)如图1,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CD是斜边AB边上的高线.用“面积法”求CD的长.
(2)如图2,在等腰三角形ABC中,AB=AC=13,BC=10,P为底边BC上的任意一点,过点P作PM⊥AB,PN⊥AC,垂足分别为M,N,连接AP,利用S△ABC=S△ABP+S△ACP,求PM+PN的值.
(3)如图3,有一直角三角形纸片ABC,∠ACB=90°,AC=4,BC=6.点D在斜边AB上,连接CD,将△ADC沿CD折叠,点A的对应点A′落在BC边上,求折叠后纸片重叠部分的面积.
每日一题24
班级 姓名 小组
24.在平面直角坐标系中,坐标轴上的三个点A(a,0),B(0,b),C(c,0)(a<0,b>0)满足|c﹣1|+(a+b)2=0,F为射线BC上的一个动点.
(1)c的值为 ,∠ABO的度数为 .
(2)如图(a),若AF⊥BC,且交OB于点E,求证:OE=OC.
(3)如图(b),若点F运动到BC的延长线上,且∠FBO=2∠FAO,O在AF的垂直平分线上,求△ABF的面积.
每日一题25
班级 姓名 小组
25.已知:在△ABC中,点E在直线AC上,点B、D、E在同一条直线上,且BA=BD,∠BAE=∠D.
【问题初探】
(1)如图1,若BE平分∠ABC,求证:∠AEB+∠BCE=180°.
请依据以下的简易思维框图,写出完整的证明过程.
【变式再探】
(2)如图2,若BE平分△ABC的外角∠ABF,交CA的延长线于点E,问:∠AEB和∠BCE的数量关系发生改变了吗?若改变,请写出正确的结论,并证明;若不改变,请说明理由.
【拓展运用】
(3)如图3,在(2)的条件下,若AB⊥BC,CD=1,求EC的长度.
每日一题21 参考答案
21.(1)①证明:如图1,
在△ACE和△BCD中,
∵,
∴△ACE≌△BCD,∴∠1=∠2,
∵∠3=∠4,∴∠BFE=∠ACE=90°,∴AF⊥BD.
②∵∠ECD=90°,BC=AC=12,DC=EC=5,
∴BD==13,
∵S△ABD=AD BC=BD AF,即
∴AF=.
(2)证明:如图4,
∵∠ACB=∠ECD,∴∠ACB+∠ACD=∠ECD+∠ACD,
∴∠BCD=∠ACE,
在△ACE≌△BCD中
∴△ACE≌△BCD,∴∠1=∠2,
∵∠3=∠4,∴∠BFA=∠BCA=90°,
∴AF⊥BD.
(3)∠AFG=45°,
如图3,过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,
∵△ACE≌△BCD,
∴S△ACE=S△BCD,AE=BD,
∵S△ACE=AE CN,
S△BCD=BD CM,
∴CM=CN,
∵CM⊥BD,CN⊥AE,
∴CF平分∠BFE,
∵AF⊥BD,
∴∠BFE=90°,
∴∠EFC=45°,
∴∠AFG=45°.
每日一题22 参考答案
22.解:(1)①BD=CE,BD⊥CE,理由如下:
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC+∠DAC,∠CAE=∠DAE+∠DAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠ABD+∠DBC=90°,
∴∠DBC+∠ACE=90°,
∴∠BFC=90°,即BD⊥CE;
②∵BD⊥CE,
∴∠BCF=∠EFD=90°,
∴BF2+CF2=BC2,DF2+EF2=DE2,
∴BF2+CF2+DF2+EF2=BC2+DE2,
∵△ABC和△ADE都是等腰直角三角形,
∴BC2=2AB2,DE2=2AD2,
∵AB=2,AD=,
∴BC2=2×22=8,=6,
∴BF2+CF2+DF2+EF2=8+6=14;
(2)连接CE,延长BD交AC于点O,交CE于点F,
同(1)可得△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠AOB=∠COF,
∴∠BAC=∠BFC=90°,
∴BD⊥CE,
∴BE2=BF2+EF2,CD2=CF2+DF2,
∴BE2+CD2=BF2+EF2+CF2+DF2,
∵BF2+CF2=BC2,DF2+EF2=DE2,
∴BE2+CD2=BC2+DE2,
∵AB=3,AD=,
∴DE=AD=2,BC=AB=3,
∴BE2+CD2==22.
每日一题23 参考答案
解:(1)如图1中,
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵CD⊥AB,
∴S△ABC= AC BC= AB CD,
∴CD==.
(2)如图2中,过点A作AH⊥BC于H.
∵AB=AC=13,BC=10,
∴BH=CH=5,
∴AH===12,
∵S△ABC= BC AH= AB PM+ AC PN,
∴×13×PM+×13×PN=×10×12,
∴PM+PN=.
(3)如图,过点D作DM⊥AC于M,DN⊥EC于N.
∵∠ACD=∠BCD,DM⊥AC,DN⊥CE,
∴DM=DN,
∵S△ACD+S△BCD=S△ACB,
∴×4×DM+×6×DN=×4×6,
∴DM=DN=,
∴S△A′CD= CA′ DN=×4×=.
每日一题24 参考答案
【解答】(1)解:∵|c﹣1|+(a+b)2=0,
∴c=1,a=﹣b,∴OA=OB,∴∠ABO=45°,
故答案为:1,45°.
(2)∵AF⊥BC,∴∠AOE=∠BFE=90°,
∵∠AEO=∠BEF,∴∠OBC=∠OAE,
在△AOE和△BOC中,
,
∴△AOE≌△BOC(AAS),
∴OE=OC;
(3)连结OF,过点F作FG⊥x轴,垂足为点G,
设∠FAO=x,则∠FBO=2∠FAO=2x,
∵O在AF的垂直平分线上,
∴AO=OF,
∴∠OAF=∠OFA=x,
∴∠GOF=∠OAF+∠OFA=2x,
∵∠FBO=2∠FAO=2x,OB=OA=OF,
∴∠OFC=∠OBF=2x,
∴∠BCO=∠COF+∠OFB=4x,
∵∠OBC+∠OCB=90°,
∴6x=90°,解得x=15°,
∴∠OBC=∠GOF=2x=30°,
∵C(1,0),
∴OC=1,
∵∠BOC=90°,∠OBC=30°,
∴BC=2OC=2,,
∴OA=OF=OB=,
同理可得:,
∴,
∴S△ABF=S△ACB+S△ACF=×AC×FG+×AC×OB=×(+1)(+)=+.
每日一题25 参考答案
证明:(1)∵BE平分∠ABC,
∴∠ABD=∠DBC,
又∵BA=BD,∠BAE=∠D,
∴△ABE≌△DBC(ASA),
∴BE=BC,
∴∠BCE=∠BEC,
∵∠AEB+∠BEC=180°,
∴∠AEB+∠BCE=180°;
(2)结论改变了,∠AEB=∠BCE,
理由如下:
∵BE平分∠ABF,
∴∠ABE=∠FBE=∠DBC,
又∵BA=BD,∠BAE=∠D,
∴△ABE≌△DBC(ASA),
∴∠AEB=∠BCE;
(3)如图3,连接AD,
∵AB⊥BC,
∴∠ABF=90°=∠ABC,
∴∠ABE=∠FBE=∠DBC=45°,
∵△ABE≌△DBC,
∴CD=AE=1,BE=BC,
∵AB=DB,∠ABD=∠ABC+∠CBD=135°,
∴∠BAD=∠BDA=22.5°,
∵BE=BC,
∴∠BEA=∠BCE,
∵∠EBF=∠E+∠BCE=45°,∠AEB=∠BCD,
∴∠BCD+∠BCE=45°=∠ACD,∠BEA=∠BCE=22.5°,
∴∠AEB=∠ADB=22.5°,
∴AE=AD=1,∠DAC=45°,
∴∠ADC=90°,
∴AC=CD=,
∴CE=AC+AE=+1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
