浙教版八年级上册数学每日一题26-30(第2章 特殊三角形)培优练习(含答案)
文档属性
| 名称 | 浙教版八年级上册数学每日一题26-30(第2章 特殊三角形)培优练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-08 16:25:22 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
每日一题26
班级 姓名 小组
26.定义:若一个三角形存在两边平方和等于第三边平方的3倍,则称此三角形为“平方倍三角形”.
(1)若一个三角形的三边长分别是,和2,这个三角形是否为平方倍三角形?请你作出判断并说明理由;
(2)若一个直角三角形是平方倍三角形,求该直角三角形的三边之比(结果按从小到大的顺序排列);
(3)如图,Rt△ABC中,∠ACB=90°,BC=5,CD为△ABC的中线,若△BCD是平方倍三角形,求△ABC的面积.
每日一题27
班级 姓名 小组
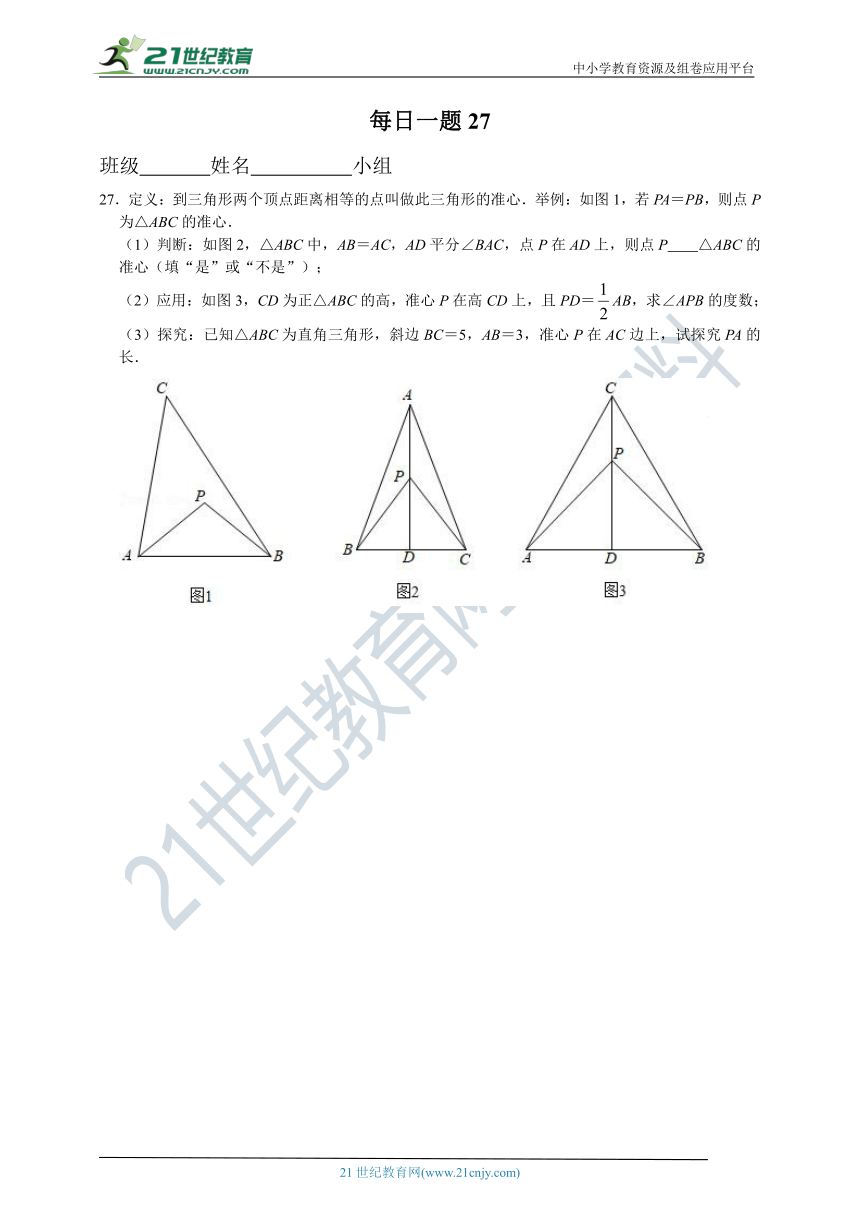
27.定义:到三角形两个顶点距离相等的点叫做此三角形的准心.举例:如图1,若PA=PB,则点P为△ABC的准心.
(1)判断:如图2,△ABC中,AB=AC,AD平分∠BAC,点P在AD上,则点P △ABC的准心(填“是”或“不是”);
(2)应用:如图3,CD为正△ABC的高,准心P在高CD上,且PD=AB,求∠APB的度数;
(3)探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准心P在AC边上,试探究PA的长.
每日一题28
班级 姓名 小组
28.已知∠A=60°,点B、C分别在∠A的两边上(不与点A重合),连接BC,作线段BC的垂直平分线;点D在∠A内部,且在△ABC外,线段BC的垂直平分线上,∠BDC=120°.
(1)求证:BC=BD;
(2)求证:AD平分∠BAC;
(3)若BC=4,
①当线段AB最大时,求四边形ABCD的面积;
②在点B的移动过程中,直接写出AD的取值范围.
每日一题29
班级 姓名 小组
29.定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A= 度;
(2)如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4.若CD是∠ACB的平分线,
①求证:△BDC是“近直角三角形”;
②求BD的长.
(3)在(2)的基础上,边AC上是否存在点E,使得△BCE也是“近直角三角形”?若存在,直接写出CE的长;若不存在,请说明理由.
每日一题30
班级 姓名 小组
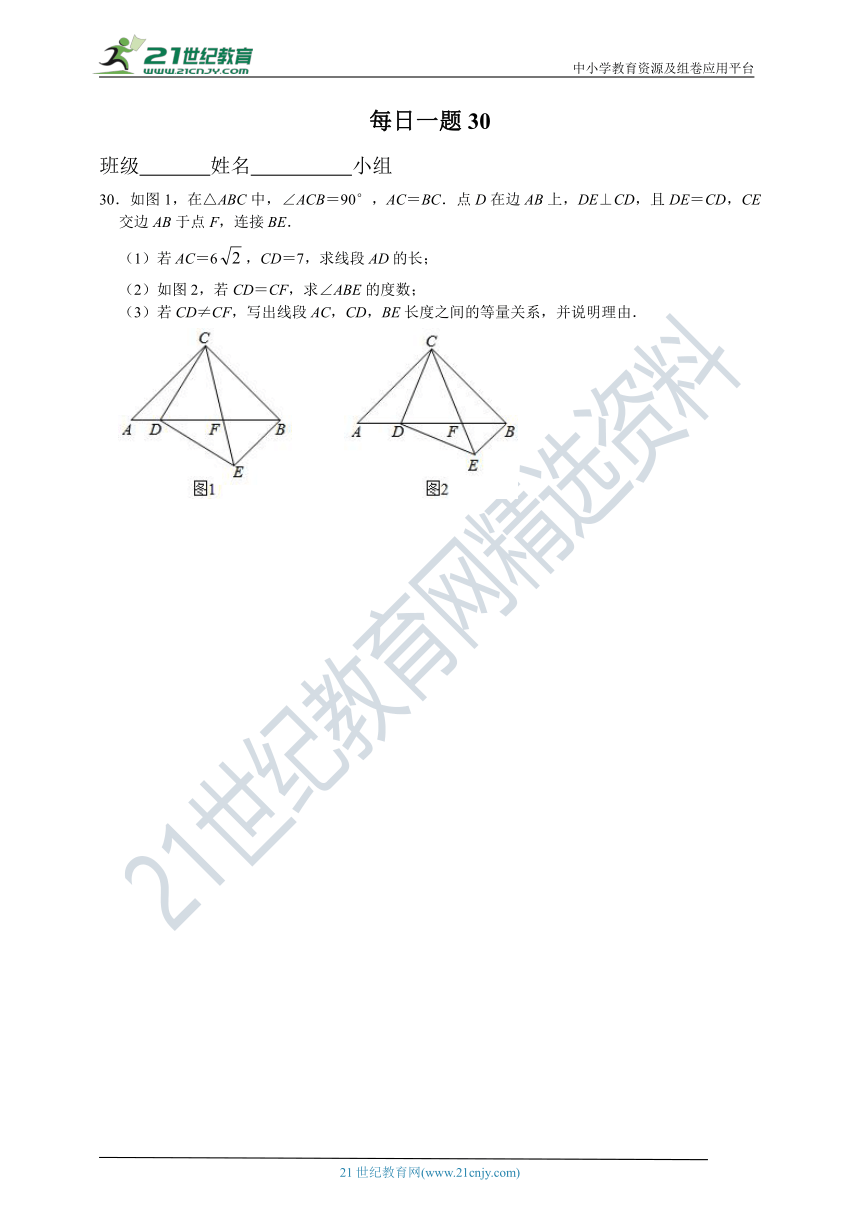
30.如图1,在△ABC中,∠ACB=90°,AC=BC.点D在边AB上,DE⊥CD,且DE=CD,CE交边AB于点F,连接BE.
(1)若AC=6,CD=7,求线段AD的长;
(2)如图2,若CD=CF,求∠ABE的度数;
(3)若CD≠CF,写出线段AC,CD,BE长度之间的等量关系,并说明理由.
每日一题26 参考答案
解:(1)结论:这个三角形是“平方倍三角形”.
理由:∵()2+22=15,3×()2=15,
∴()2+22=3×()2,
∴这个三角形是“平方倍三角形”.
(2)设两直角边长为:a,b,斜边长为:c,
∵△ABC为“平方倍三角形”.
∴a2+b2=c2,且c2+a2=3b2,
∴2a2+b2=3b2,
∴b=a,
∴c=a,
∴a:b:c=1:1:.
(3)∵Rt△ABC中,∠ACB=90°,BC=5,点D为AB的中点,△BCD是“平方倍三角形”,
∴当AD=BD=DC,CD2+BD2=3×52时,
解得:BD=DC=,
则AB=5,
故AC===5,
则△ABC的面积为:×5×5=.
当AD=BD=DC,CD2+BC2=3×BD2时,
解得:BD=DC=,
则AB=5,
故AC=5,
则△ABC的面积为:×5×5=.
故△ABC的面积为或.
每日一题27 参考答案
解:(1)如图2中,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD,
∴PB=PC,
∴点P是△ABC的准心,
故答案为:是.
(2)如图3中,
∵CA=CB,CD⊥AB,
∴AD=BD,
∵PD=AB,
∴AD=PD=DB,
∴∠APD=∠BPD=45°,
∴∠APB=90°.
(3)如图4中,
∵BC=5,AB=3,
∴AC===4,
①若PB=PC,设PA=x,则x2+32=(4﹣x)2,
∴x=,即PA=,
②若PA=PC,则PA=2,
③若PA=PB,由图知,在Rt△PAB中,不可能.
故PA=2或.
每日一题28 参考答案
28.(1)证明:过点D作DE⊥BC于E.
∵DC=DB,DE⊥CB,
∴CE=EB,∠CDE=∠BDE=∠CDB=60°,
∴EC=BE=BD,
∴BC=2EC=BD.
(2)证明:如图2中,连接AD,过点D作DE⊥AC于点E,作⊥DF⊥AB于F.
∵∠EAF=60°,∠AED=∠AFD=90°,
∴∠EDF=∠CDB=120°,
∴∠CDE=∠FDB,
在△DEC和△DFB中,
,
∴△DEC≌△DFB(AAS)
∴DE=DF,
∵DE⊥AE,DF⊥AB,
∴AD平分∠CAB.
(3)解:①当BC⊥AC时,AB的值最大,最大值AB==8,
此时AC=AB=4,四边形ABDC的面积=×4×4+×4×2=12.
②当AD⊥BC时,AD的值最大,最大值为8,
当点C与A重合或点B与A重合时,AD=CD=4,
∴4<AD≤8.
每日一题29 参考答案
29.解:(1)∠B不可能是α或β,
当∠A=α时,∠C=β=50°,α+2β=90°,不成立;
故∠A=β,∠C=α,α+2β=90°,则β=20°,
故答案为20;
(2)①如图1,设∠ACD=∠DCB=β,∠B=α,
则α+2β=90°,故△BDC是“近直角三角形”;
②如图2,过点D作DM⊥BC于点M,
∵CD平分∠ACB,DM⊥BC,DA⊥CA,
∴AD=DM,
在Rt△ACD和Rt△MCD中,
,
∴Rt△ACD≌Rt△MCD(HL),
∴AC=CM=4,
∵AB=3,AC=4,
∴BC===5,
∴BM=1,
设AD=DM=x,
∵DM2+BM2=DB2,
∴x2+12=(3﹣x)2,
∴x=,
∴BD=AB﹣AD=3﹣;
(3)存在,理由:
①如图,作∠ABC的平分线BE,则△BCE是“近直角三角形”,
过点E作EF⊥BC于点F,
则AE=EF,AB=BF=3,设CE=x,∴AE=EF=4﹣x,
∵EF2+CF2=CE2,∴(4﹣x)2+22=x2,
∴x=;
②如图,作∠ABE=∠C,则△BCE是“近直角三角形”,
延长CA至G,使EA=AG,则BE=BG,
设CE=x,则AG=AE=4﹣x,
∵BG2=AG2+AB2,BG2=CG2﹣BC2,
∴BG2=(4﹣x)2+32,BG2=CG2﹣BC2,
∴(4﹣x)2+32=(8﹣x)2﹣52,∴x=.
综合以上可得CE的长为或.
每日一题30 参考答案
(1)解:过点C作CM⊥AB于M,如图1,
∵∠ACB=90°,AC=BC,AC=6,
∴AB=AC=12,
∵CM⊥AB,
∴CM=AM=BM=AB=6,
∴DM===,
∴AD=AM﹣DM=6﹣;
(2)证明:过点C作CM⊥AB于M,过E作EN⊥AB于N,如图2,
则∠CMD=∠DNE=90°,
∴∠MCD+∠MDC=90°,
∵DE⊥CD,
∴∠MDC+∠NDE=90°,
∴∠MCD=∠NDE,
又∵CD=DE,
∴△CDM≌△DEN(AAS),
∴CM=DN,DM=EN,
∴DM+MN=CM,
∵∠ACB=90°,AC=BC
∴∠ABC=45°,
由(1)知,CM=AM=BM=AB,
∴BM=MN+BN=CM=DM+MN,
∴DM=BN=EN,
∴△BNE是等腰直角三角形,
∴∠ABE=45°;
(3)解:AC2+BE2=2CD2,理由如下:
过点C作CM⊥AB于M,过E作EN⊥AB于N,如图3,
由(2)可知:EN=BN=DM,BE2=EN2+BN2=2EN2=2DM2,
∴DM2=BE2,
在Rt△ACM中,CM=AM,AC2=CM2+AM2,
在Rt△CDM中,CM=AM,CD2=CM2+DM2,
∴CD2=AC2+BE2,
∴AC2+BE2=2CD2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题26
班级 姓名 小组
26.定义:若一个三角形存在两边平方和等于第三边平方的3倍,则称此三角形为“平方倍三角形”.
(1)若一个三角形的三边长分别是,和2,这个三角形是否为平方倍三角形?请你作出判断并说明理由;
(2)若一个直角三角形是平方倍三角形,求该直角三角形的三边之比(结果按从小到大的顺序排列);
(3)如图,Rt△ABC中,∠ACB=90°,BC=5,CD为△ABC的中线,若△BCD是平方倍三角形,求△ABC的面积.
每日一题27
班级 姓名 小组
27.定义:到三角形两个顶点距离相等的点叫做此三角形的准心.举例:如图1,若PA=PB,则点P为△ABC的准心.
(1)判断:如图2,△ABC中,AB=AC,AD平分∠BAC,点P在AD上,则点P △ABC的准心(填“是”或“不是”);
(2)应用:如图3,CD为正△ABC的高,准心P在高CD上,且PD=AB,求∠APB的度数;
(3)探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准心P在AC边上,试探究PA的长.
每日一题28
班级 姓名 小组
28.已知∠A=60°,点B、C分别在∠A的两边上(不与点A重合),连接BC,作线段BC的垂直平分线;点D在∠A内部,且在△ABC外,线段BC的垂直平分线上,∠BDC=120°.
(1)求证:BC=BD;
(2)求证:AD平分∠BAC;
(3)若BC=4,
①当线段AB最大时,求四边形ABCD的面积;
②在点B的移动过程中,直接写出AD的取值范围.
每日一题29
班级 姓名 小组
29.定义:如果一个三角形中有两个内角α,β满足α+2β=90°,那我们称这个三角形为“近直角三角形”.
(1)若△ABC是“近直角三角形”,∠B>90°,∠C=50°,则∠A= 度;
(2)如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4.若CD是∠ACB的平分线,
①求证:△BDC是“近直角三角形”;
②求BD的长.
(3)在(2)的基础上,边AC上是否存在点E,使得△BCE也是“近直角三角形”?若存在,直接写出CE的长;若不存在,请说明理由.
每日一题30
班级 姓名 小组
30.如图1,在△ABC中,∠ACB=90°,AC=BC.点D在边AB上,DE⊥CD,且DE=CD,CE交边AB于点F,连接BE.
(1)若AC=6,CD=7,求线段AD的长;
(2)如图2,若CD=CF,求∠ABE的度数;
(3)若CD≠CF,写出线段AC,CD,BE长度之间的等量关系,并说明理由.
每日一题26 参考答案
解:(1)结论:这个三角形是“平方倍三角形”.
理由:∵()2+22=15,3×()2=15,
∴()2+22=3×()2,
∴这个三角形是“平方倍三角形”.
(2)设两直角边长为:a,b,斜边长为:c,
∵△ABC为“平方倍三角形”.
∴a2+b2=c2,且c2+a2=3b2,
∴2a2+b2=3b2,
∴b=a,
∴c=a,
∴a:b:c=1:1:.
(3)∵Rt△ABC中,∠ACB=90°,BC=5,点D为AB的中点,△BCD是“平方倍三角形”,
∴当AD=BD=DC,CD2+BD2=3×52时,
解得:BD=DC=,
则AB=5,
故AC===5,
则△ABC的面积为:×5×5=.
当AD=BD=DC,CD2+BC2=3×BD2时,
解得:BD=DC=,
则AB=5,
故AC=5,
则△ABC的面积为:×5×5=.
故△ABC的面积为或.
每日一题27 参考答案
解:(1)如图2中,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD,
∴PB=PC,
∴点P是△ABC的准心,
故答案为:是.
(2)如图3中,
∵CA=CB,CD⊥AB,
∴AD=BD,
∵PD=AB,
∴AD=PD=DB,
∴∠APD=∠BPD=45°,
∴∠APB=90°.
(3)如图4中,
∵BC=5,AB=3,
∴AC===4,
①若PB=PC,设PA=x,则x2+32=(4﹣x)2,
∴x=,即PA=,
②若PA=PC,则PA=2,
③若PA=PB,由图知,在Rt△PAB中,不可能.
故PA=2或.
每日一题28 参考答案
28.(1)证明:过点D作DE⊥BC于E.
∵DC=DB,DE⊥CB,
∴CE=EB,∠CDE=∠BDE=∠CDB=60°,
∴EC=BE=BD,
∴BC=2EC=BD.
(2)证明:如图2中,连接AD,过点D作DE⊥AC于点E,作⊥DF⊥AB于F.
∵∠EAF=60°,∠AED=∠AFD=90°,
∴∠EDF=∠CDB=120°,
∴∠CDE=∠FDB,
在△DEC和△DFB中,
,
∴△DEC≌△DFB(AAS)
∴DE=DF,
∵DE⊥AE,DF⊥AB,
∴AD平分∠CAB.
(3)解:①当BC⊥AC时,AB的值最大,最大值AB==8,
此时AC=AB=4,四边形ABDC的面积=×4×4+×4×2=12.
②当AD⊥BC时,AD的值最大,最大值为8,
当点C与A重合或点B与A重合时,AD=CD=4,
∴4<AD≤8.
每日一题29 参考答案
29.解:(1)∠B不可能是α或β,
当∠A=α时,∠C=β=50°,α+2β=90°,不成立;
故∠A=β,∠C=α,α+2β=90°,则β=20°,
故答案为20;
(2)①如图1,设∠ACD=∠DCB=β,∠B=α,
则α+2β=90°,故△BDC是“近直角三角形”;
②如图2,过点D作DM⊥BC于点M,
∵CD平分∠ACB,DM⊥BC,DA⊥CA,
∴AD=DM,
在Rt△ACD和Rt△MCD中,
,
∴Rt△ACD≌Rt△MCD(HL),
∴AC=CM=4,
∵AB=3,AC=4,
∴BC===5,
∴BM=1,
设AD=DM=x,
∵DM2+BM2=DB2,
∴x2+12=(3﹣x)2,
∴x=,
∴BD=AB﹣AD=3﹣;
(3)存在,理由:
①如图,作∠ABC的平分线BE,则△BCE是“近直角三角形”,
过点E作EF⊥BC于点F,
则AE=EF,AB=BF=3,设CE=x,∴AE=EF=4﹣x,
∵EF2+CF2=CE2,∴(4﹣x)2+22=x2,
∴x=;
②如图,作∠ABE=∠C,则△BCE是“近直角三角形”,
延长CA至G,使EA=AG,则BE=BG,
设CE=x,则AG=AE=4﹣x,
∵BG2=AG2+AB2,BG2=CG2﹣BC2,
∴BG2=(4﹣x)2+32,BG2=CG2﹣BC2,
∴(4﹣x)2+32=(8﹣x)2﹣52,∴x=.
综合以上可得CE的长为或.
每日一题30 参考答案
(1)解:过点C作CM⊥AB于M,如图1,
∵∠ACB=90°,AC=BC,AC=6,
∴AB=AC=12,
∵CM⊥AB,
∴CM=AM=BM=AB=6,
∴DM===,
∴AD=AM﹣DM=6﹣;
(2)证明:过点C作CM⊥AB于M,过E作EN⊥AB于N,如图2,
则∠CMD=∠DNE=90°,
∴∠MCD+∠MDC=90°,
∵DE⊥CD,
∴∠MDC+∠NDE=90°,
∴∠MCD=∠NDE,
又∵CD=DE,
∴△CDM≌△DEN(AAS),
∴CM=DN,DM=EN,
∴DM+MN=CM,
∵∠ACB=90°,AC=BC
∴∠ABC=45°,
由(1)知,CM=AM=BM=AB,
∴BM=MN+BN=CM=DM+MN,
∴DM=BN=EN,
∴△BNE是等腰直角三角形,
∴∠ABE=45°;
(3)解:AC2+BE2=2CD2,理由如下:
过点C作CM⊥AB于M,过E作EN⊥AB于N,如图3,
由(2)可知:EN=BN=DM,BE2=EN2+BN2=2EN2=2DM2,
∴DM2=BE2,
在Rt△ACM中,CM=AM,AC2=CM2+AM2,
在Rt△CDM中,CM=AM,CD2=CM2+DM2,
∴CD2=AC2+BE2,
∴AC2+BE2=2CD2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
