浙教版八年级上传数学每日一题31-35(第5章 一次函数)培优训练(含答案)
文档属性
| 名称 | 浙教版八年级上传数学每日一题31-35(第5章 一次函数)培优训练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 10:48:11 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
每日一题31
班级 姓名 小组
31.如图1,在平面直角坐标系xOy中,点O为坐标原点,直线AB:y=kx+3与直线AC:y=﹣2x+b交于点A(2,n),与x轴分别交于点B(﹣6,0)和点C.点D为线段BC上一动点,将△ABD沿直线AD翻折得到△ADE,线段AE交x轴于点F.
(1)求直线AC的函数表达式;
(2)若点D在线段BO上;
①当点E落在y轴上时,求点E的坐标;
②当△DEF与△AFC的面积相等时,求线段AD的长;
(3)若△DEF为直角三角形,请直接写出点D的坐标.
每日一题32
班级 姓名 小组
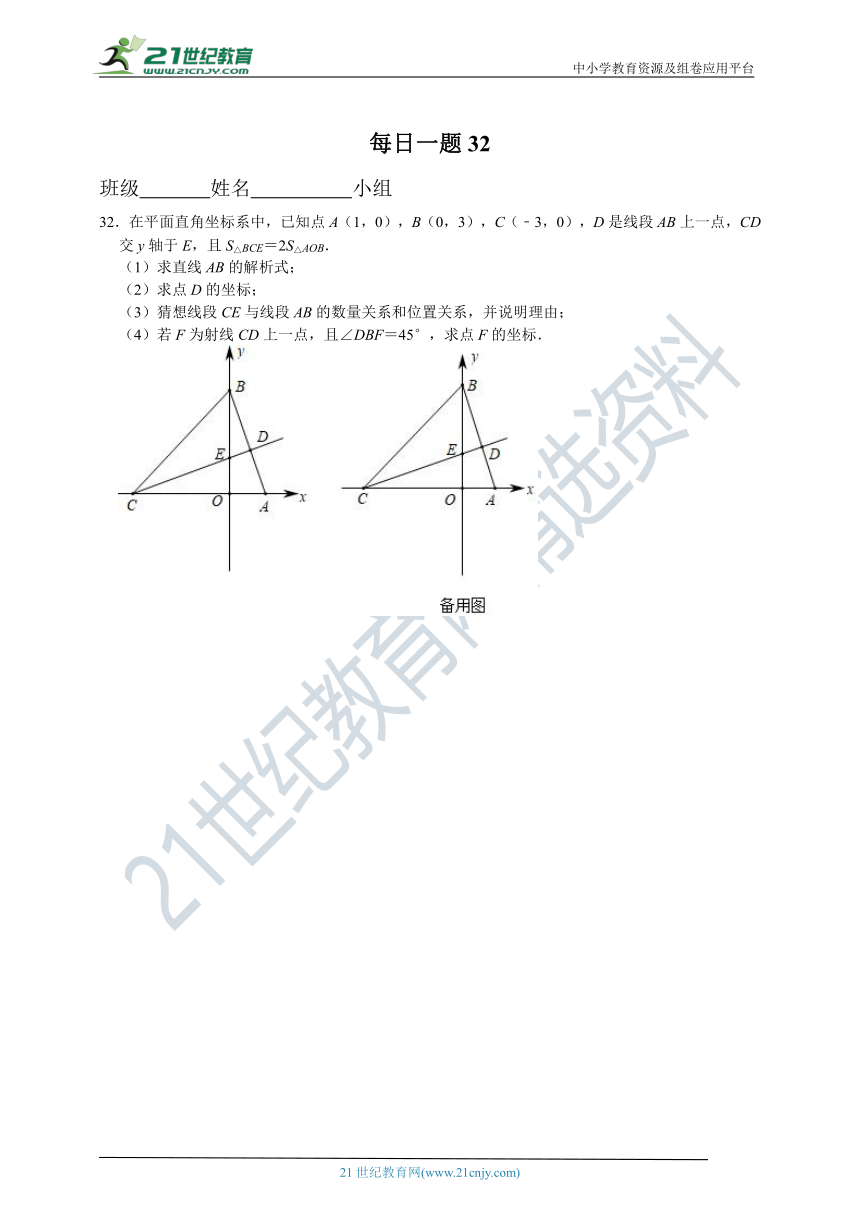
32.在平面直角坐标系中,已知点A(1,0),B(0,3),C(﹣3,0),D是线段AB上一点,CD交y轴于E,且S△BCE=2S△AOB.
(1)求直线AB的解析式;
(2)求点D的坐标;
(3)猜想线段CE与线段AB的数量关系和位置关系,并说明理由;
(4)若F为射线CD上一点,且∠DBF=45°,求点F的坐标.
每日一题33
班级 姓名 小组
33.已知直线l:y=kx+3k+1(k>0)经过定点A.
(1)探求定点A的坐标.把函数表达式作如下变形:y=kx+3k+1=k(x+3)+1,当x=﹣3时,可以消去k,求出y=1,则定点A的坐标为 .
(2)如图1,已知△BCD各顶点的坐标分别为B(0,1),C(﹣4,1),D(0,4),直线l将△BCD的周长分成7:17两部分,求k的值.
(3)如图2,设直线l与y轴交于点P,另一条直线y=(k﹣1)x+3k﹣2与y轴交于点Q,交直线l于点E,点F是EQ的中点.当点P从(0,5)沿y轴正方向运动到(0,10)时,求点F运动经过的路径长.
每日一题34
班级 姓名 小组
34.如图,一次函数的图象过A(3,0),B(0,3)两点.
(1)求直线AB的函数表达式;
(2)直线y=﹣3x﹣3交x轴于点C,E为直线AB上一动点.
①求CE的最小值;
②D是直线y=﹣3x﹣3上任意一点,F为直线AB上另一动点,若△DEF是以2为直角边长的等腰直角三角形,求D点的坐标.
每日一题35
班级 姓名 小组
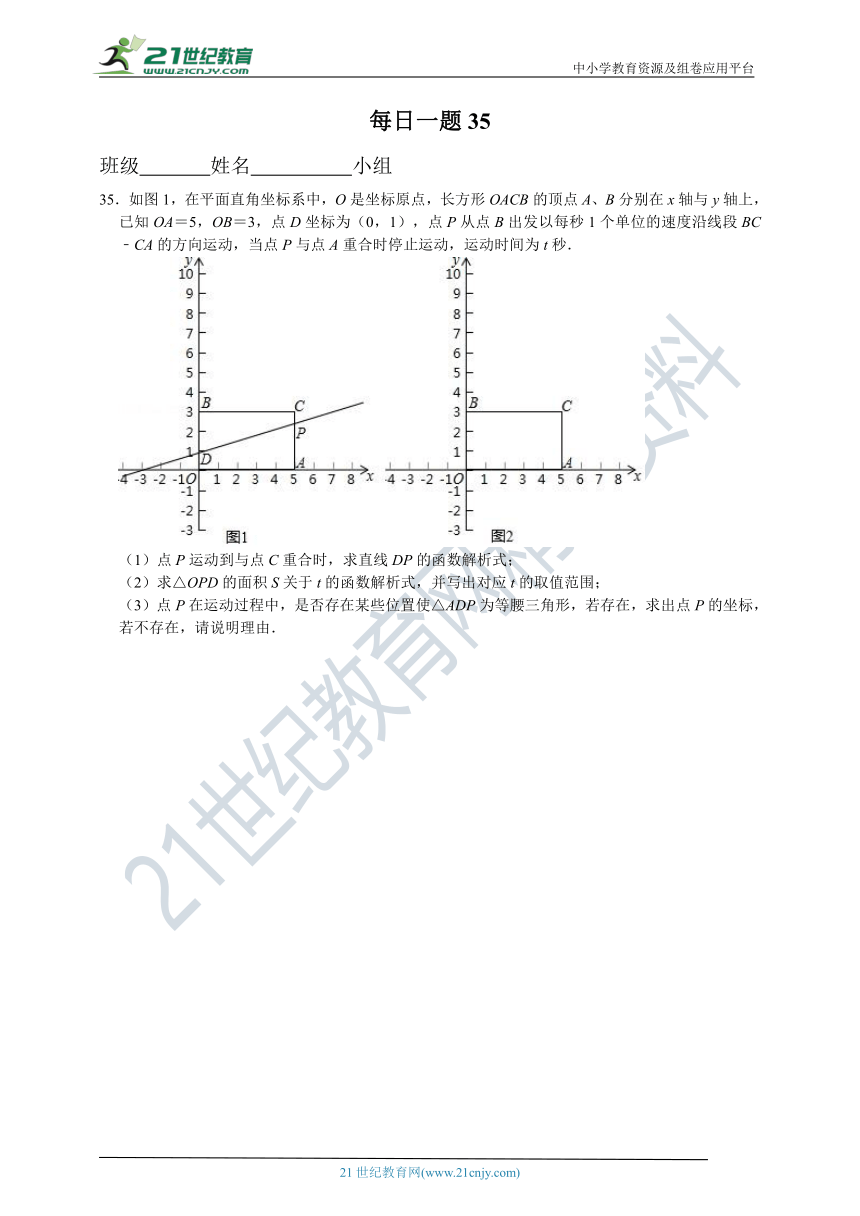
35.如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=5,OB=3,点D坐标为(0,1),点P从点B出发以每秒1个单位的速度沿线段BC﹣CA的方向运动,当点P与点A重合时停止运动,运动时间为t秒.
(1)点P运动到与点C重合时,求直线DP的函数解析式;
(2)求△OPD的面积S关于t的函数解析式,并写出对应t的取值范围;
(3)点P在运动过程中,是否存在某些位置使△ADP为等腰三角形,若存在,求出点P的坐标,若不存在,请说明理由.
每日一题31 参考答案
31.解:(1)把B(﹣6,0)代入kx+3,∴﹣6+3=0,∴k=,
∴直线AB解析式:y=x+3,把点A(2,n)代入y=x+3,∴n=4,∴A(2,4),
把(2,4)代入y=﹣2x+b得,﹣4+b=4,∴b=8,
∴直线AC的函数表达式:y=﹣2x+8.
(2)①如图,过点A作AH⊥y轴于点H,
∴AH=2,AE2=AB2=(﹣6﹣2)2+(0﹣4)2=80,∴HE==2,
∴OE=HE﹣OH=2﹣4,∴E点的坐标为(0,4﹣2),
②∵S△DEF=S△APC,∴S△DEF+S△ADF=S△AFC+S△ADF,即S△ADE=S△ADC,
∵S△ABD=S△ADE,∴S△ABD=S△ADC,∴D为BC中点,
∵y=﹣2x+8,当y=0时,∴﹣2x+8=0,∴x=4,∴C(4,0),
∵B(﹣6,0),∴D(,0),即D(﹣1,0),∴AD==5.
(3)由对折得,∠E=∠ABD=90°,∴△DEF为直角三角形,分两种情况讨论:
当∠EDF=90°时,如图,由对折可得,∠ADB=∠ADE==135°,
∴∠ADO=135°﹣90°=45°,过点A作AG⊥BC于G,∴AG=DG=4,
∵OG=2,∴OD=2,∴D(﹣2,0),当∠DFE=90°时,
由对折得,AE=AB==4,BD=DE,∴EF=4﹣4,
由A、B两点坐标可得:BF=2﹣(﹣6)=8,
设DF=m,则BD=8﹣m,
∴DE=8﹣m,
∴(8﹣m)2=m2+(4﹣4)2,
∴m=2﹣2,
∴OD=DF﹣OF=2﹣2﹣2=2﹣4,
∴D(4﹣2,0),
综上,D(﹣2,0)或(4﹣2,0).
每日一题32 参考答案
32.解:(1)设直线AB的函数解析式为:y=kx+b,
则,∴,∴直线AB的函数解析式为:y=﹣3x+3;
(2)设E(0,t),
∵A(1,0),B(0,3),∴OA=1,OB=3,∴S△AOB=,
∵S△BCE=2S△AOB,∴S△BCE=3,∴,
解得t=1,∴E(0,1),
设直线CE的函数解析式为:y=mx+n,将C、E的坐标代入得:
,∴,∴直线CE的函数解析式为:y=x+1,
当x+1=﹣3x+3时,∴x=,则y=,∴D(),
(3)猜想:CE=AB,CE⊥AB,理由如下:
∵OE=OA=1,OC=OB=3,∠COE=∠BOA=90°,∴△COE≌△BOA(SAS),
∴CE=AB,∠OCE=∠OBA,
∵∠OBA+∠BAO=90°,∴∠OCE+∠BAO=90°,∴∠CDA=90°,∴CE⊥AB;
(4)在射线CD上存在两个F点,使∠DBF=45°,
如图,当点F在线段CD上时,过点D作GH∥y轴,过点B、F分别作GH的垂线,垂足分别为G、H点,
∵CD⊥AB,∠DBF=45°,∴∠DBF=∠DFB=45°,∴BD=DF,
∵∠BDG+∠FDH=90°,∠BDG+∠DBG=90°,∴∠FDH=∠DBG,
又∵∠G=∠H ∴△BDG≌△DFH(AAS),
∴FH=DG=3﹣=,DH=BG=,∴点F(﹣,),
当点F在CD的延长线上时,由对称性可知F(,),
综上点F的坐标为:(﹣,)或(,),
每日一题33 参考答案
33.解:(1)∵x=﹣3时,y的值与k无关,都为1,∴定点A(﹣3,1),故答案为:(﹣3,1);
(2)∵A(﹣3,1),B(0,1),C(﹣4,1),D(0,4),∴AB=3,BC=4,BD=3,
∵∠CDB=90°,∴CD===5,
∴△BCD的周长为BD+CD+BC=12,
∵直线l将△BCD的周长分成7:17两部分,
∴两部分的长分别为:12×=,12×=,
①若AB+BN=,如图:∴3+BN=,∴BN=,
∴N(0,),将N(0,)代入y=kx+3k+1得:=3k+1,解得k=,
②若AC+CM=,如图:∴1+CM=,
∴CM=,∴CM=CD,∴M为CD中点,
∴M(﹣2,),把M(﹣2,)代入y=kx+3k+1得:
=﹣2k+3k+1,解得:k=,综上所述,k的值为或;
(3)由得,
∴E(﹣3,1),∴E与A重合,
∵点F是EQ的中点,∴xF=﹣,
而由y=kx+3k+1、y=(k﹣1)x+3k﹣2可得P(0,3k+1)、Q(0,3k﹣2),
∴PQ=3,
∵点P从(0,5)沿y轴正方向运动到(0,10),
∴Q从(0,2)运动到(0,7),
∴F从(﹣,)运动到(﹣,4),
∴F运动的路程为:4﹣=.
每日一题34 参考答案
34.解:(1)设直线AB的函数表达式为:y=kx+b,
由题意可得:解得:∴直线AB的函数表达式为:y=﹣x+3;
(2)①如图1,当CE⊥AB时,CE有最小值,
∵直线y=﹣3x﹣3交x轴于点C,
∴点C(﹣1,0),且A(3,0),B(0,3)
∴AC=4,OA=OB=3,∴∠BAO=45°,且CE⊥AB,
∴AC=CE,∴CE==2,∴CE的最小值为2;
②设直线AB与直线y=﹣3x﹣3交于点H,
∴ 解得:∴点H(﹣3,6)
如图2,若点E是直角顶点时,
∵△DEF是以2为直角边长的等腰直角三角形,
∴DE=2,DE⊥AB,
当点D在点B下方时,由①可知点D与点C重合时,△DEF是等腰直角三角形,
∴点D(﹣1,0)
当点D在点B上方时,
∵DE=D'E'=2,∠DHE=∠D'HE',且∠D'E'H=∠DEH,
∴△DEH≌△D'E'H(AAS)
∴D'H=DH,且点H(﹣3,6),点D(﹣1,0)
∴点D'(﹣5,12)
如图3,若点D是直角顶点,则DE=2,DE∥AC,
设点D坐标(a,﹣3a﹣3)
∴点E(a﹣2,﹣3a﹣3)或(a+2,﹣3a﹣3),且点E在直线y=﹣x+3上,
∴﹣3a﹣3=﹣a+2+3,或﹣3a﹣3=﹣a﹣2+3
∴a=﹣﹣3,或a=﹣3,
∴点D坐标(﹣﹣3,3+6)或(﹣3,﹣3+6)
综上所述:点D坐标为:(﹣﹣3,3+6)或(﹣3,﹣3+6)或(﹣1,0)或(﹣5,12).
每日一题35 参考答案
35.解:(1)∵OA=5,OB=3,且四边形OACB为长方形,∴C(5,3),
∴当点P与点C重合时,P点坐标为(5,3),
∵D(0,1),∴可设直线DP解析式为y=kx+1,
∴3=5k+1,解得k=,∴直线DP解析式为y=x+1;
(2)当点P在线段BC上时,即0≤t≤5时,如图1,
则BP=t,且OD=1,
∴S= OD BP=×1×t=t,
当点P在线段AC上时,即5<t≤8时,则S=OD BC=×1×5=,
∴S=;
(3)当点P在线段BC上时,如图2,
则可设P点坐标为(t,3)(0<t≤5),
∵A(5,0),D(0,1),
∴DP==,AP==,AD==,
当△APD为等腰三角形时,则有DP=AP、DP=AD和AP=AD三种情况,
①当DP=AP时,则有=,解得t=3,此时P点坐标为(3,3);
②当DP=AD时,则有=,解得t=﹣(舍去)或t=,此时P点坐标为(,3);
③当AP=AD时,则有=,解得t=5+(舍去)或t=5﹣,此时P点坐标为(5﹣,3);
当点P在线段AC上时,则AP<AD,只有AD=DP,
∴D在线段AC的垂直平分线上,
∴线段AP的中点坐标为(5,1),
∴P点坐标为(5,2);
综上可知存在满足条件的点P,其坐标为(3,3)或(,3)或(5﹣,3)或(5,2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题31
班级 姓名 小组
31.如图1,在平面直角坐标系xOy中,点O为坐标原点,直线AB:y=kx+3与直线AC:y=﹣2x+b交于点A(2,n),与x轴分别交于点B(﹣6,0)和点C.点D为线段BC上一动点,将△ABD沿直线AD翻折得到△ADE,线段AE交x轴于点F.
(1)求直线AC的函数表达式;
(2)若点D在线段BO上;
①当点E落在y轴上时,求点E的坐标;
②当△DEF与△AFC的面积相等时,求线段AD的长;
(3)若△DEF为直角三角形,请直接写出点D的坐标.
每日一题32
班级 姓名 小组
32.在平面直角坐标系中,已知点A(1,0),B(0,3),C(﹣3,0),D是线段AB上一点,CD交y轴于E,且S△BCE=2S△AOB.
(1)求直线AB的解析式;
(2)求点D的坐标;
(3)猜想线段CE与线段AB的数量关系和位置关系,并说明理由;
(4)若F为射线CD上一点,且∠DBF=45°,求点F的坐标.
每日一题33
班级 姓名 小组
33.已知直线l:y=kx+3k+1(k>0)经过定点A.
(1)探求定点A的坐标.把函数表达式作如下变形:y=kx+3k+1=k(x+3)+1,当x=﹣3时,可以消去k,求出y=1,则定点A的坐标为 .
(2)如图1,已知△BCD各顶点的坐标分别为B(0,1),C(﹣4,1),D(0,4),直线l将△BCD的周长分成7:17两部分,求k的值.
(3)如图2,设直线l与y轴交于点P,另一条直线y=(k﹣1)x+3k﹣2与y轴交于点Q,交直线l于点E,点F是EQ的中点.当点P从(0,5)沿y轴正方向运动到(0,10)时,求点F运动经过的路径长.
每日一题34
班级 姓名 小组
34.如图,一次函数的图象过A(3,0),B(0,3)两点.
(1)求直线AB的函数表达式;
(2)直线y=﹣3x﹣3交x轴于点C,E为直线AB上一动点.
①求CE的最小值;
②D是直线y=﹣3x﹣3上任意一点,F为直线AB上另一动点,若△DEF是以2为直角边长的等腰直角三角形,求D点的坐标.
每日一题35
班级 姓名 小组
35.如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=5,OB=3,点D坐标为(0,1),点P从点B出发以每秒1个单位的速度沿线段BC﹣CA的方向运动,当点P与点A重合时停止运动,运动时间为t秒.
(1)点P运动到与点C重合时,求直线DP的函数解析式;
(2)求△OPD的面积S关于t的函数解析式,并写出对应t的取值范围;
(3)点P在运动过程中,是否存在某些位置使△ADP为等腰三角形,若存在,求出点P的坐标,若不存在,请说明理由.
每日一题31 参考答案
31.解:(1)把B(﹣6,0)代入kx+3,∴﹣6+3=0,∴k=,
∴直线AB解析式:y=x+3,把点A(2,n)代入y=x+3,∴n=4,∴A(2,4),
把(2,4)代入y=﹣2x+b得,﹣4+b=4,∴b=8,
∴直线AC的函数表达式:y=﹣2x+8.
(2)①如图,过点A作AH⊥y轴于点H,
∴AH=2,AE2=AB2=(﹣6﹣2)2+(0﹣4)2=80,∴HE==2,
∴OE=HE﹣OH=2﹣4,∴E点的坐标为(0,4﹣2),
②∵S△DEF=S△APC,∴S△DEF+S△ADF=S△AFC+S△ADF,即S△ADE=S△ADC,
∵S△ABD=S△ADE,∴S△ABD=S△ADC,∴D为BC中点,
∵y=﹣2x+8,当y=0时,∴﹣2x+8=0,∴x=4,∴C(4,0),
∵B(﹣6,0),∴D(,0),即D(﹣1,0),∴AD==5.
(3)由对折得,∠E=∠ABD=90°,∴△DEF为直角三角形,分两种情况讨论:
当∠EDF=90°时,如图,由对折可得,∠ADB=∠ADE==135°,
∴∠ADO=135°﹣90°=45°,过点A作AG⊥BC于G,∴AG=DG=4,
∵OG=2,∴OD=2,∴D(﹣2,0),当∠DFE=90°时,
由对折得,AE=AB==4,BD=DE,∴EF=4﹣4,
由A、B两点坐标可得:BF=2﹣(﹣6)=8,
设DF=m,则BD=8﹣m,
∴DE=8﹣m,
∴(8﹣m)2=m2+(4﹣4)2,
∴m=2﹣2,
∴OD=DF﹣OF=2﹣2﹣2=2﹣4,
∴D(4﹣2,0),
综上,D(﹣2,0)或(4﹣2,0).
每日一题32 参考答案
32.解:(1)设直线AB的函数解析式为:y=kx+b,
则,∴,∴直线AB的函数解析式为:y=﹣3x+3;
(2)设E(0,t),
∵A(1,0),B(0,3),∴OA=1,OB=3,∴S△AOB=,
∵S△BCE=2S△AOB,∴S△BCE=3,∴,
解得t=1,∴E(0,1),
设直线CE的函数解析式为:y=mx+n,将C、E的坐标代入得:
,∴,∴直线CE的函数解析式为:y=x+1,
当x+1=﹣3x+3时,∴x=,则y=,∴D(),
(3)猜想:CE=AB,CE⊥AB,理由如下:
∵OE=OA=1,OC=OB=3,∠COE=∠BOA=90°,∴△COE≌△BOA(SAS),
∴CE=AB,∠OCE=∠OBA,
∵∠OBA+∠BAO=90°,∴∠OCE+∠BAO=90°,∴∠CDA=90°,∴CE⊥AB;
(4)在射线CD上存在两个F点,使∠DBF=45°,
如图,当点F在线段CD上时,过点D作GH∥y轴,过点B、F分别作GH的垂线,垂足分别为G、H点,
∵CD⊥AB,∠DBF=45°,∴∠DBF=∠DFB=45°,∴BD=DF,
∵∠BDG+∠FDH=90°,∠BDG+∠DBG=90°,∴∠FDH=∠DBG,
又∵∠G=∠H ∴△BDG≌△DFH(AAS),
∴FH=DG=3﹣=,DH=BG=,∴点F(﹣,),
当点F在CD的延长线上时,由对称性可知F(,),
综上点F的坐标为:(﹣,)或(,),
每日一题33 参考答案
33.解:(1)∵x=﹣3时,y的值与k无关,都为1,∴定点A(﹣3,1),故答案为:(﹣3,1);
(2)∵A(﹣3,1),B(0,1),C(﹣4,1),D(0,4),∴AB=3,BC=4,BD=3,
∵∠CDB=90°,∴CD===5,
∴△BCD的周长为BD+CD+BC=12,
∵直线l将△BCD的周长分成7:17两部分,
∴两部分的长分别为:12×=,12×=,
①若AB+BN=,如图:∴3+BN=,∴BN=,
∴N(0,),将N(0,)代入y=kx+3k+1得:=3k+1,解得k=,
②若AC+CM=,如图:∴1+CM=,
∴CM=,∴CM=CD,∴M为CD中点,
∴M(﹣2,),把M(﹣2,)代入y=kx+3k+1得:
=﹣2k+3k+1,解得:k=,综上所述,k的值为或;
(3)由得,
∴E(﹣3,1),∴E与A重合,
∵点F是EQ的中点,∴xF=﹣,
而由y=kx+3k+1、y=(k﹣1)x+3k﹣2可得P(0,3k+1)、Q(0,3k﹣2),
∴PQ=3,
∵点P从(0,5)沿y轴正方向运动到(0,10),
∴Q从(0,2)运动到(0,7),
∴F从(﹣,)运动到(﹣,4),
∴F运动的路程为:4﹣=.
每日一题34 参考答案
34.解:(1)设直线AB的函数表达式为:y=kx+b,
由题意可得:解得:∴直线AB的函数表达式为:y=﹣x+3;
(2)①如图1,当CE⊥AB时,CE有最小值,
∵直线y=﹣3x﹣3交x轴于点C,
∴点C(﹣1,0),且A(3,0),B(0,3)
∴AC=4,OA=OB=3,∴∠BAO=45°,且CE⊥AB,
∴AC=CE,∴CE==2,∴CE的最小值为2;
②设直线AB与直线y=﹣3x﹣3交于点H,
∴ 解得:∴点H(﹣3,6)
如图2,若点E是直角顶点时,
∵△DEF是以2为直角边长的等腰直角三角形,
∴DE=2,DE⊥AB,
当点D在点B下方时,由①可知点D与点C重合时,△DEF是等腰直角三角形,
∴点D(﹣1,0)
当点D在点B上方时,
∵DE=D'E'=2,∠DHE=∠D'HE',且∠D'E'H=∠DEH,
∴△DEH≌△D'E'H(AAS)
∴D'H=DH,且点H(﹣3,6),点D(﹣1,0)
∴点D'(﹣5,12)
如图3,若点D是直角顶点,则DE=2,DE∥AC,
设点D坐标(a,﹣3a﹣3)
∴点E(a﹣2,﹣3a﹣3)或(a+2,﹣3a﹣3),且点E在直线y=﹣x+3上,
∴﹣3a﹣3=﹣a+2+3,或﹣3a﹣3=﹣a﹣2+3
∴a=﹣﹣3,或a=﹣3,
∴点D坐标(﹣﹣3,3+6)或(﹣3,﹣3+6)
综上所述:点D坐标为:(﹣﹣3,3+6)或(﹣3,﹣3+6)或(﹣1,0)或(﹣5,12).
每日一题35 参考答案
35.解:(1)∵OA=5,OB=3,且四边形OACB为长方形,∴C(5,3),
∴当点P与点C重合时,P点坐标为(5,3),
∵D(0,1),∴可设直线DP解析式为y=kx+1,
∴3=5k+1,解得k=,∴直线DP解析式为y=x+1;
(2)当点P在线段BC上时,即0≤t≤5时,如图1,
则BP=t,且OD=1,
∴S= OD BP=×1×t=t,
当点P在线段AC上时,即5<t≤8时,则S=OD BC=×1×5=,
∴S=;
(3)当点P在线段BC上时,如图2,
则可设P点坐标为(t,3)(0<t≤5),
∵A(5,0),D(0,1),
∴DP==,AP==,AD==,
当△APD为等腰三角形时,则有DP=AP、DP=AD和AP=AD三种情况,
①当DP=AP时,则有=,解得t=3,此时P点坐标为(3,3);
②当DP=AD时,则有=,解得t=﹣(舍去)或t=,此时P点坐标为(,3);
③当AP=AD时,则有=,解得t=5+(舍去)或t=5﹣,此时P点坐标为(5﹣,3);
当点P在线段AC上时,则AP<AD,只有AD=DP,
∴D在线段AC的垂直平分线上,
∴线段AP的中点坐标为(5,1),
∴P点坐标为(5,2);
综上可知存在满足条件的点P,其坐标为(3,3)或(,3)或(5﹣,3)或(5,2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
