浙教版八年级数学每日一题36-40(第5章 一次函数)培优练习(含答案)
文档属性
| 名称 | 浙教版八年级数学每日一题36-40(第5章 一次函数)培优练习(含答案) | 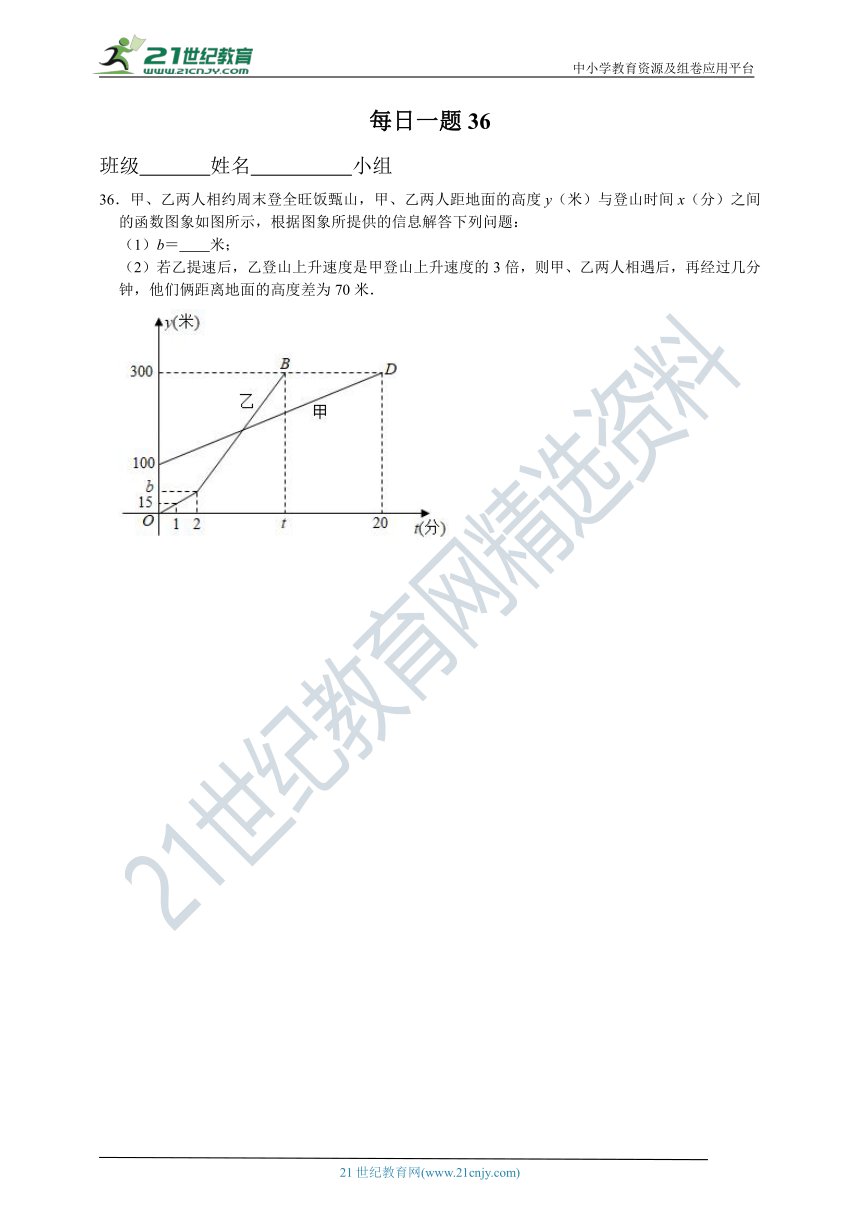 | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 13:49:18 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
每日一题36
班级 姓名 小组
36.甲、乙两人相约周末登全旺饭甄山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)b= 米;
(2)若乙提速后,乙登山上升速度是甲登山上升速度的3倍,则甲、乙两人相遇后,再经过几分钟,他们俩距离地面的高度差为70米.
每日一题37
班级 姓名 小组
37.如图1,已知一条笔直的公路上有A,B,C三地,B地位于A、C两地之间.甲车从A地出发,驶向C地,同时乙车从C地出发驶向B地,到达B地并停留了0.2小时后,按原路返回C地.两车沿公路匀速行驶,甲车的速度比乙车的速度慢15千米/时,设两车行驶时间为x小时.图2中线段OD和折线E﹣F﹣G﹣H分别表示甲、乙两车各自到A地的距离y(千米)与行驶的时间x(小时)的函数图象,请结合图象信息,解答下列问题:
(1)A、C两地之间的路程为 千米,乙车的速度是 千米/时;
(2)求乙车从B地返回C地时(线段GH)的路程y(千米)与时间x(小时)之间的函数关系式(不需要写出自变量的取值范围);
(3)出发多少小时后,行驶中的两车之间距离等于20千米?
每日一题38
班级 姓名 小组
38.甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地,甲、乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,请结合图象信息解答下列问题;
①直接写出a的值,并求甲车的速度;
②求图中线段EF所表示的函数y关于x的解析式;并直接写出自变量x的取值范围;
③乙车出发后多少小时与甲车相距15千米?
每日一题39
班级 姓名 小组
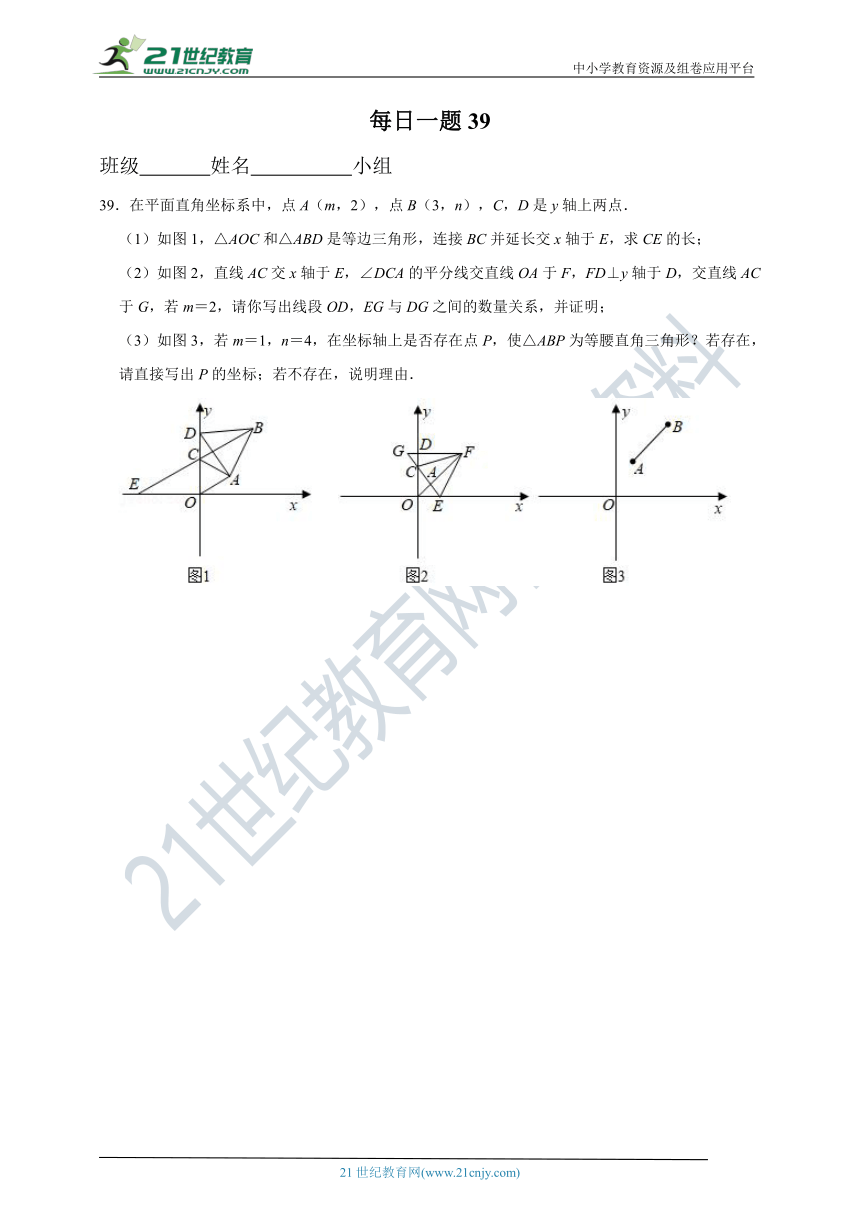
39.在平面直角坐标系中,点A(m,2),点B(3,n),C,D是y轴上两点.
(1)如图1,△AOC和△ABD是等边三角形,连接BC并延长交x轴于E,求CE的长;
(2)如图2,直线AC交x轴于E,∠DCA的平分线交直线OA于F,FD⊥y轴于D,交直线AC于G,若m=2,请你写出线段OD,EG与DG之间的数量关系,并证明;
(3)如图3,若m=1,n=4,在坐标轴上是否存在点P,使△ABP为等腰直角三角形?若存在,请直接写出P的坐标;若不存在,说明理由.
每日一题40
班级 姓名 小组
26.定义:图象与x轴有两个交点的函数y=叫做关于m的对称函数,它与x轴负半轴交点记为A,与x轴正半轴交点记为B,
(1)关于l的对称函数y=与直线x=1交于点C,如图.
①直接写出点的坐标:A( ,0);B( ,0);C(1, );
②P为关于l的对称函数图象上一点(点P不与点C重合),当S△ABC=S△ABP时,求点P的坐标;
(2)当直线y=x与关于m的对称函数有两个交点时,求m的取值范围.
每日一题36参考答案
36.解:(1)b=15×2=30,
故答案为:30;
(2)甲登山上升速度是:(300﹣100)÷20=10(米/分)
乙提速后速度:10×3=30,
∴t=2+(300﹣30)÷30=11,
设甲关系式:y=kx+b,
把(0,100),(20.300)代入y=kx+b得,
,
解得k=10x+100,(0≤x≤20),
设乙关系式:m=ax(0≤x≤2),
把(1,15)代入得,a=15,
∴m=15x,
设n=hx+p(2<x≤11),
把(2,30)(11,300)代入得h=30,p=﹣30,
∴n=30x﹣30,
当10x+100=30x﹣30时,即x=6.5时甲乙两人相遇
①30x﹣30﹣(10x+100)=70,
解得x=10,10-6,5=3.5
②300﹣(10x+100)=70,
解得x=13,13-6.5=6.5
综上所述:甲、乙两人相遇后,再经:3.5分、6.5分时俩距离地面的高度差为70米.
每日一题37参考答案
37.解:(1)由图2甲车到A地的距离y(千米)与行驶的时间x(小时)的函数图象可知,AC之间的路程为120千米,
∴甲的行驶速度为120÷2=60千米/时,
∴乙的行驶速度为60+15=75千米/时,
故答案为:120;75;
(2)∵乙的行驶速度为75千米/时,
∴A地到B地的距离=120﹣75×1=45千米,
∴F(1,45),G(1.2,45),
∵乙的速度不变,
∴k=75,
设 y=75x+b,
将G(1.2,45)代入得,
45=75×1.2+b,
解得:b=﹣45,
∴乙车从B地返回C地时,函数关系式为y=75x﹣45;
(3)∵甲的速度为60千米/时,
∴y=60x,
∵乙的速度为75千米/时,EF段经过E(0,120),
∴y=120﹣75x,
∴120﹣75x=60x,
解得:x=,
∴两车经过时相遇,
①当0<x<时,乙从C向B地行驶,
∴﹣75x+120﹣60x=20,
解得:x=,
②当x=1时,乙在B点,甲在距离A点60千米处,
∴此时距离差为60﹣45=15千米≠20,
③当1<x<1.2时,60x﹣45=20,
解得:x=,
④当1.2<x<2时,由于乙的速度大于甲的速度,
∴乙距离甲越来越近,
∴60x﹣(75x﹣45)=20,
解得:x=,
综上,出发时或时或时,两车相距20千米.
每日一题38参考答案
38.解:①a=4+0.4=4.5,
甲车的速度=(千米/小时);
②设乙开始的速度为v千米/小时,
则4v+(7﹣4.5)(v﹣50)=460,解得v=90(千米/小时),
4v=360,
则D(4,360),E(4.5,360),
设直线EF的解析式为y=kx+b,
把E(4.5,360),F(7,460)代入得,
解得,
所以线段EF所表示的y与x的函数关系式为y=40x+180(4.5≤x≤7);
③甲车前40分钟的路程为(千米),则C(0,40),
设直线CF的解析式为y=mx+n,
把C(0,40),F(7,460)代入得,
解得,
所以直线CF的解析式为y=60x+40,
易得直线OD的解析式为y=90x(0≤x≤4),
设甲乙两车中途相遇点为G,由60x+40=90x,解得x=,即乙车出发小时后,甲乙两车相遇,
当乙车在OG段时,由60x+40﹣90x=15,解得x=,介于0~小时之间,符合题意;
当乙车在GD段时,由90x﹣(60x+40)=15,解得x=,介于~4小时之间,符合题意;
当乙车在DE段时,由360﹣(60x+40)=15,解得x=,不介于4~4.5之间,不符合题意;
当乙车在EF段时,由40x+180﹣(60x+40)=15,解得x=,介于4.5~7之间,符合题意.
所以乙车出发小时或小时或小时,乙与甲车相距15千米.
每日一题39参考答案
39.解:(1)如图,过点A作AM⊥OD,垂足为点M,
∵△AOC和△ABD是等边三角形,
∴AC=OA=OC,AD=AB,∠CAO=∠DAB=60°,
∴∠CAB=∠DAO,且AC=AO,AD=AB,
∴△AOD≌△ACB(SAS),
∴∠ACB=∠DOA=60°,
∴∠ECO=180°﹣∠ACO﹣∠ACB=60°,
∵△AOC是等边三角形,AM⊥OD,
∴OM=CM,∵点A(m,2),∴OM=CM=2,∴CO=4,
∵=,∴CE=2CO=8;
(2)结论:GE=OD+GD,
理由:如图,连接EF,过点F作FH⊥CE,FM⊥OE,
∵m=2,∴A(2,2),且O(0,0),
∴直线OA解析式为:y=x,∴OA平分∠COE,
∴∠COF=45°,且DF⊥OC,∴∠DFO=∠COF=45°,
∴OD=DF,
∵CF平分∠DCE,DF⊥CD,FH⊥CE,∴DF=FH,
∵OA平分∠COE,DF⊥OD,FM⊥OE,∴DF=FM,
∴FM=FH,且FM⊥OE,FH⊥CE,∴EF平分∠CEM,
∴∠GEF=∠FEM,
∵DF⊥OD,OM⊥OD,∴DF∥OM,
∴∠DFE=∠FEM,∴∠GEF=∠DFE,∴GF=GE,
∴GE=GD+DF=GD+OD;
(3)如图,过点A作AN⊥x轴,
∵m=1,n=4,
∴点A(1,2),点B(3,4),
∴AB==2,
若AP=BA,则NP==2,
∵点N(1,0),
∴P1(3,0),P2(﹣1,0),
若AP=BP,则点P在AB的垂直平分线上,
∵点A(1,2),点B(3,4),设P(m,0),
则有(m﹣1)2+22=(m﹣3)2+42,
解得m=5,
∴点P3(5,0),
综上所述:点P的坐标为(﹣1,0)或(3,0)或(5,0).
每日一题40参考答案
【解答】解:令±2x+4=0,解得x=2或﹣1,
故点A、B的坐标分别为(﹣2,0)、(2,0),
∵函数与x轴负半轴交点为A,与x轴正半轴交点记B,则﹣2<m≤2;
(1)①从图象看,x=1时,y=﹣2x+4=2,故点C(1,2);
故答案为﹣2,2,2;
②当点P在x轴上方时,
∵S△ABC=S△ABP,则点P、C所在的直线与x轴平行,
而点C(1,2),
故点P的纵坐标为2,
当y=2x+4=2时,x=﹣1,故点P(﹣1,2);
当点P在x轴下方时,
同理可得:﹣2=±2x+4,解得x=±3,
故点P的坐标为(﹣1,2)或(﹣3,﹣2)或(3,﹣2);
(2)当直线y=x与关于m的对称函数有两个交点时,
当m>0时,点C(m,4﹣2m),
将点C的坐标代入y=x得:4﹣2m=m,解得m=;
故m≤,
当m<0时,m=2m+4,
解得m=﹣4,
∵﹣4<m≤2,
∴m的取值范围是﹣4<m≤.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题36
班级 姓名 小组
36.甲、乙两人相约周末登全旺饭甄山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)b= 米;
(2)若乙提速后,乙登山上升速度是甲登山上升速度的3倍,则甲、乙两人相遇后,再经过几分钟,他们俩距离地面的高度差为70米.
每日一题37
班级 姓名 小组
37.如图1,已知一条笔直的公路上有A,B,C三地,B地位于A、C两地之间.甲车从A地出发,驶向C地,同时乙车从C地出发驶向B地,到达B地并停留了0.2小时后,按原路返回C地.两车沿公路匀速行驶,甲车的速度比乙车的速度慢15千米/时,设两车行驶时间为x小时.图2中线段OD和折线E﹣F﹣G﹣H分别表示甲、乙两车各自到A地的距离y(千米)与行驶的时间x(小时)的函数图象,请结合图象信息,解答下列问题:
(1)A、C两地之间的路程为 千米,乙车的速度是 千米/时;
(2)求乙车从B地返回C地时(线段GH)的路程y(千米)与时间x(小时)之间的函数关系式(不需要写出自变量的取值范围);
(3)出发多少小时后,行驶中的两车之间距离等于20千米?
每日一题38
班级 姓名 小组
38.甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地,甲、乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,请结合图象信息解答下列问题;
①直接写出a的值,并求甲车的速度;
②求图中线段EF所表示的函数y关于x的解析式;并直接写出自变量x的取值范围;
③乙车出发后多少小时与甲车相距15千米?
每日一题39
班级 姓名 小组
39.在平面直角坐标系中,点A(m,2),点B(3,n),C,D是y轴上两点.
(1)如图1,△AOC和△ABD是等边三角形,连接BC并延长交x轴于E,求CE的长;
(2)如图2,直线AC交x轴于E,∠DCA的平分线交直线OA于F,FD⊥y轴于D,交直线AC于G,若m=2,请你写出线段OD,EG与DG之间的数量关系,并证明;
(3)如图3,若m=1,n=4,在坐标轴上是否存在点P,使△ABP为等腰直角三角形?若存在,请直接写出P的坐标;若不存在,说明理由.
每日一题40
班级 姓名 小组
26.定义:图象与x轴有两个交点的函数y=叫做关于m的对称函数,它与x轴负半轴交点记为A,与x轴正半轴交点记为B,
(1)关于l的对称函数y=与直线x=1交于点C,如图.
①直接写出点的坐标:A( ,0);B( ,0);C(1, );
②P为关于l的对称函数图象上一点(点P不与点C重合),当S△ABC=S△ABP时,求点P的坐标;
(2)当直线y=x与关于m的对称函数有两个交点时,求m的取值范围.
每日一题36参考答案
36.解:(1)b=15×2=30,
故答案为:30;
(2)甲登山上升速度是:(300﹣100)÷20=10(米/分)
乙提速后速度:10×3=30,
∴t=2+(300﹣30)÷30=11,
设甲关系式:y=kx+b,
把(0,100),(20.300)代入y=kx+b得,
,
解得k=10x+100,(0≤x≤20),
设乙关系式:m=ax(0≤x≤2),
把(1,15)代入得,a=15,
∴m=15x,
设n=hx+p(2<x≤11),
把(2,30)(11,300)代入得h=30,p=﹣30,
∴n=30x﹣30,
当10x+100=30x﹣30时,即x=6.5时甲乙两人相遇
①30x﹣30﹣(10x+100)=70,
解得x=10,10-6,5=3.5
②300﹣(10x+100)=70,
解得x=13,13-6.5=6.5
综上所述:甲、乙两人相遇后,再经:3.5分、6.5分时俩距离地面的高度差为70米.
每日一题37参考答案
37.解:(1)由图2甲车到A地的距离y(千米)与行驶的时间x(小时)的函数图象可知,AC之间的路程为120千米,
∴甲的行驶速度为120÷2=60千米/时,
∴乙的行驶速度为60+15=75千米/时,
故答案为:120;75;
(2)∵乙的行驶速度为75千米/时,
∴A地到B地的距离=120﹣75×1=45千米,
∴F(1,45),G(1.2,45),
∵乙的速度不变,
∴k=75,
设 y=75x+b,
将G(1.2,45)代入得,
45=75×1.2+b,
解得:b=﹣45,
∴乙车从B地返回C地时,函数关系式为y=75x﹣45;
(3)∵甲的速度为60千米/时,
∴y=60x,
∵乙的速度为75千米/时,EF段经过E(0,120),
∴y=120﹣75x,
∴120﹣75x=60x,
解得:x=,
∴两车经过时相遇,
①当0<x<时,乙从C向B地行驶,
∴﹣75x+120﹣60x=20,
解得:x=,
②当x=1时,乙在B点,甲在距离A点60千米处,
∴此时距离差为60﹣45=15千米≠20,
③当1<x<1.2时,60x﹣45=20,
解得:x=,
④当1.2<x<2时,由于乙的速度大于甲的速度,
∴乙距离甲越来越近,
∴60x﹣(75x﹣45)=20,
解得:x=,
综上,出发时或时或时,两车相距20千米.
每日一题38参考答案
38.解:①a=4+0.4=4.5,
甲车的速度=(千米/小时);
②设乙开始的速度为v千米/小时,
则4v+(7﹣4.5)(v﹣50)=460,解得v=90(千米/小时),
4v=360,
则D(4,360),E(4.5,360),
设直线EF的解析式为y=kx+b,
把E(4.5,360),F(7,460)代入得,
解得,
所以线段EF所表示的y与x的函数关系式为y=40x+180(4.5≤x≤7);
③甲车前40分钟的路程为(千米),则C(0,40),
设直线CF的解析式为y=mx+n,
把C(0,40),F(7,460)代入得,
解得,
所以直线CF的解析式为y=60x+40,
易得直线OD的解析式为y=90x(0≤x≤4),
设甲乙两车中途相遇点为G,由60x+40=90x,解得x=,即乙车出发小时后,甲乙两车相遇,
当乙车在OG段时,由60x+40﹣90x=15,解得x=,介于0~小时之间,符合题意;
当乙车在GD段时,由90x﹣(60x+40)=15,解得x=,介于~4小时之间,符合题意;
当乙车在DE段时,由360﹣(60x+40)=15,解得x=,不介于4~4.5之间,不符合题意;
当乙车在EF段时,由40x+180﹣(60x+40)=15,解得x=,介于4.5~7之间,符合题意.
所以乙车出发小时或小时或小时,乙与甲车相距15千米.
每日一题39参考答案
39.解:(1)如图,过点A作AM⊥OD,垂足为点M,
∵△AOC和△ABD是等边三角形,
∴AC=OA=OC,AD=AB,∠CAO=∠DAB=60°,
∴∠CAB=∠DAO,且AC=AO,AD=AB,
∴△AOD≌△ACB(SAS),
∴∠ACB=∠DOA=60°,
∴∠ECO=180°﹣∠ACO﹣∠ACB=60°,
∵△AOC是等边三角形,AM⊥OD,
∴OM=CM,∵点A(m,2),∴OM=CM=2,∴CO=4,
∵=,∴CE=2CO=8;
(2)结论:GE=OD+GD,
理由:如图,连接EF,过点F作FH⊥CE,FM⊥OE,
∵m=2,∴A(2,2),且O(0,0),
∴直线OA解析式为:y=x,∴OA平分∠COE,
∴∠COF=45°,且DF⊥OC,∴∠DFO=∠COF=45°,
∴OD=DF,
∵CF平分∠DCE,DF⊥CD,FH⊥CE,∴DF=FH,
∵OA平分∠COE,DF⊥OD,FM⊥OE,∴DF=FM,
∴FM=FH,且FM⊥OE,FH⊥CE,∴EF平分∠CEM,
∴∠GEF=∠FEM,
∵DF⊥OD,OM⊥OD,∴DF∥OM,
∴∠DFE=∠FEM,∴∠GEF=∠DFE,∴GF=GE,
∴GE=GD+DF=GD+OD;
(3)如图,过点A作AN⊥x轴,
∵m=1,n=4,
∴点A(1,2),点B(3,4),
∴AB==2,
若AP=BA,则NP==2,
∵点N(1,0),
∴P1(3,0),P2(﹣1,0),
若AP=BP,则点P在AB的垂直平分线上,
∵点A(1,2),点B(3,4),设P(m,0),
则有(m﹣1)2+22=(m﹣3)2+42,
解得m=5,
∴点P3(5,0),
综上所述:点P的坐标为(﹣1,0)或(3,0)或(5,0).
每日一题40参考答案
【解答】解:令±2x+4=0,解得x=2或﹣1,
故点A、B的坐标分别为(﹣2,0)、(2,0),
∵函数与x轴负半轴交点为A,与x轴正半轴交点记B,则﹣2<m≤2;
(1)①从图象看,x=1时,y=﹣2x+4=2,故点C(1,2);
故答案为﹣2,2,2;
②当点P在x轴上方时,
∵S△ABC=S△ABP,则点P、C所在的直线与x轴平行,
而点C(1,2),
故点P的纵坐标为2,
当y=2x+4=2时,x=﹣1,故点P(﹣1,2);
当点P在x轴下方时,
同理可得:﹣2=±2x+4,解得x=±3,
故点P的坐标为(﹣1,2)或(﹣3,﹣2)或(3,﹣2);
(2)当直线y=x与关于m的对称函数有两个交点时,
当m>0时,点C(m,4﹣2m),
将点C的坐标代入y=x得:4﹣2m=m,解得m=;
故m≤,
当m<0时,m=2m+4,
解得m=﹣4,
∵﹣4<m≤2,
∴m的取值范围是﹣4<m≤.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
