浙教版八年级数学每日一题41-45(第5章 一次函数)培优练习(含答案)
文档属性
| 名称 | 浙教版八年级数学每日一题41-45(第5章 一次函数)培优练习(含答案) | 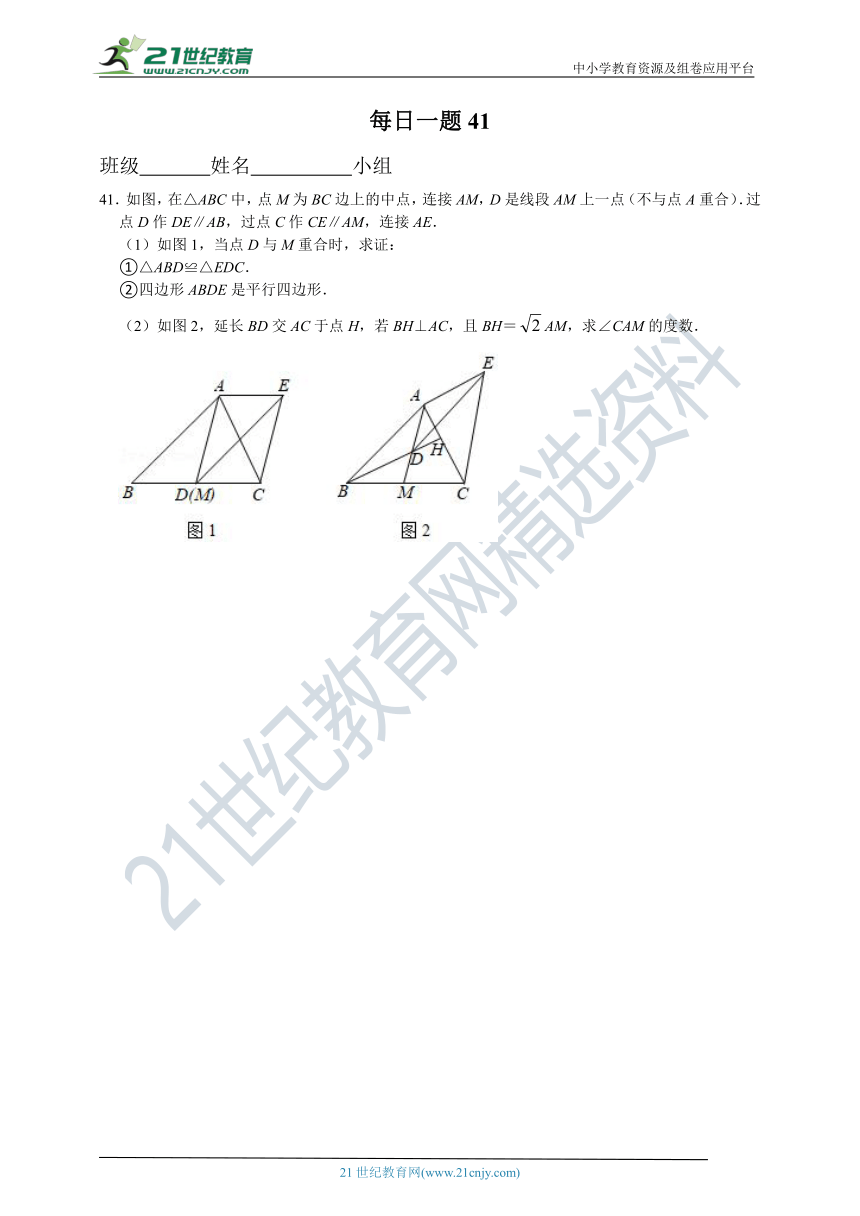 | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 13:52:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
每日一题41
班级 姓名 小组
41.如图,在△ABC中,点M为BC边上的中点,连接AM,D是线段AM上一点(不与点A重合).过点D作DE∥AB,过点C作CE∥AM,连接AE.
(1)如图1,当点D与M重合时,求证:
①△ABD≌△EDC.
②四边形ABDE是平行四边形.
(2)如图2,延长BD交AC于点H,若BH⊥AC,且BH=AM,求∠CAM的度数.
每日一题42
班级 姓名 小组
42.如图,一次函数的图象经过点A(4,0),B(0,3).以线段AB为边在第一象限内作等腰直角三角形ABC,∠BAC=90°.若第二象限内有一点P(a,),且△ABP的面积与△ABC的面积相等.
(1)求直线AB的函数表达式.
(2)求a的值.
(3)在x轴上是否存在点M,使△MAC为等腰三角形,若存在,直接写出点M的坐标;若不存在.请说明理由.
每日一题43
班级 姓名 小组
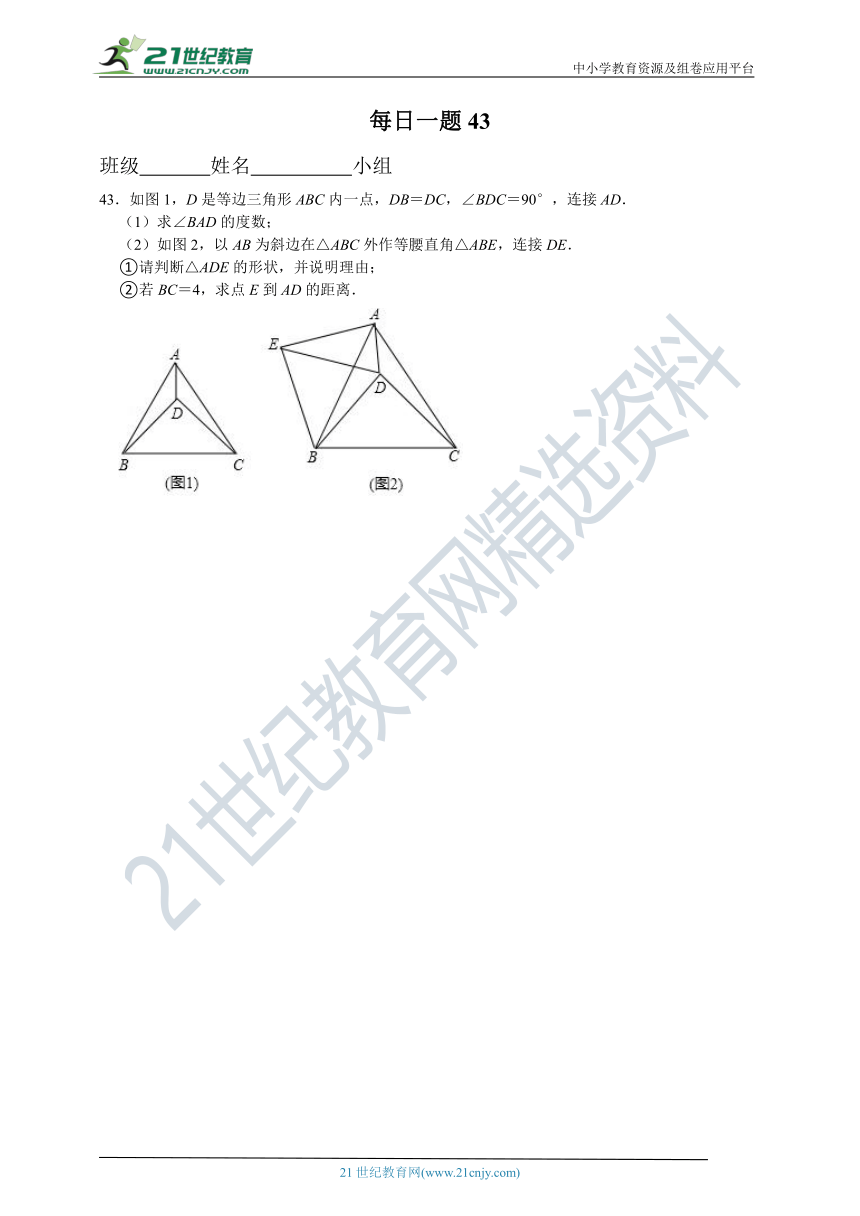
43.如图1,D是等边三角形ABC内一点,DB=DC,∠BDC=90°,连接AD.
(1)求∠BAD的度数;
(2)如图2,以AB为斜边在△ABC外作等腰直角△ABE,连接DE.
①请判断△ADE的形状,并说明理由;
②若BC=4,求点E到AD的距离.
每日一题44
班级 姓名 小组
44.如图,A(4,0),B(0,4),直线y=x+1与x轴、y轴、直线AB分别交于点C、E、D.
(1)求直线BC的解析式及D点的坐标;
(2)求四边形OADE的面积;
(3)F是OA的中点,过点F作直线l,若l恰好将四边形OADE分成面积比为1:4的两部分,求直线l的解析式.
每日一题45
班级 姓名 小组
45.在等腰梯形OABC中,OA∥BC,AB=OC,在建立如图的平面直角坐标系中,A(8,0),B(6,6),直线AC与y轴交于点D.
(1)直接写出C点的坐标,并求出直线AC的解析式;
(2)点P的直线AC上,且△OCP的面积为12,请求出点P的坐标.
(3)在y轴右侧的直线AC上是否存在一点M点,使得△OCM为等腰三角形?若有,请求出M点的坐标,若没有,请说明理由.
每日一题41参考答案
41.(1)①如图1中,
∵DE∥AB,
∴∠EDC=∠ABM,
∵CE∥AM,
∴∠ECD=∠ADB,
∵AM是△ABC的中线,且D与M重合,
∴BD=DC,
在△ABD与△EDC中,
,
∴△ABD≌△EDC(ASA).
②由①得△ABD≌△EDC,
∴AB=ED,
∵AB∥ED,
∴四边形ABDE是平行四边形.
(2)如图2中,取线段HC的中点I,连接MI,
∵BM=MC,
∴MI是△BHC的中位线,
∴MI∥BH,,
∵BH⊥AC,且.
∴,MI⊥AC,
∴∠CAM=45°.
每日一题42参考答案
42.解:(1)设直线AB的解析式为y=kx+b(k≠0),
将点A(4,0),B(0,3)代入解析式,
得,解得,∴直线AB的解析式为y=﹣x+3;
(2)如图,过点P作PD⊥x轴交于点D,∵A(4,0),B(0,3),∴OA=4,OB=3,
∵等腰直角三角形ABC,∠BAC=90°,由勾股定理可得AB=AC=5,
∵P(a,),∴PD=,OD=﹣a,
S△ABP=S梯形PDOB+S△ABO﹣S△APD=(OB+PD)×OD+×OA×OB﹣×PD×AD=(3+)×(﹣a)+×3×4﹣××(4﹣a)=﹣a+,
S△ABC=×AB×AC=,
∵△ABP的面积与△ABC的面积相等,∴﹣a+=,∴a=﹣5;
(3)①当AC=CM时,过C点作CE⊥x轴交于点E,
∵∠BOA=∠AEC=90°,∠BAC=90°,∴∠BAO=∠ACE,
∵AB=AC,∴△ABO≌△CAE(AAS),
∴AE=BO,∵BO=3,∴AE=3,
∵AE是等腰三角形ACM边AM的中点,∴AM=6,∴M(10,0);
②当AC=AM时,∵AC=5,∴AM=5,∴M(9,0)或M(﹣1,0);
③当CM=AM时,作AC的垂线平分线HM,分别交AC、x轴于点H、M,∵AC=5,∴AH=,
∵∠BOA=∠AHM=90°,∴∠OBA=∠HAM,
∴cos∠OBA=cos∠HAM,即==,∴AM=,
∴MO=4+=,∴M(,0);
综上所述:△MAC为等腰三角形时,M点的坐标为(10,0)或(9,0)或(,0)或(﹣1,0).
每日一题43参考答案
43.解:(1)∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,AB=BC=AC,
在△ADB和△ADC中,,
∴△ADB≌△ADC(SSS),
∴∠BAD=∠CAD=∠BAC=×60°=30°;
(2)①△ADE是等腰三角形,理由如下:
∵DB=DC,∠BDC=90°,
∴△CBD是以BC为斜边的等腰直角三角形,∠DBC=45°,
∵以AB为斜边在△ABC外作等腰直角△ABE,AB=BC,
∴∠EBA=45°,AE=BE=DB=DC,
∴∠EBA+∠ABD=∠ABD+∠DBC=∠ABC=60°,即∠EBD=60°,
∴△BDE是等边三角形,∴DE=BE,∴AE=DE,∴△ADE是等腰三角形;
②延长AD交BC于点F,过点E作EN⊥AD于N,如图2所示:
∵∠BAD=∠CAD,
∴AF是∠BAC的平分线,AF⊥BC,BF=BC=2,
∵∠DBC=45°,
∴△BDF是等腰直角三角形,
∴DF=BF=2,
AF===2,
∴AD=AF﹣DF=2﹣2,
∵△ADE是等腰三角形,
∴DN=AN=AD=﹣1,
∵DE=BD=BF=2,
∴EN===1+,
∴点E到AD的距离为1+.
每日一题44 参考答案
44.解:(1)∵直线y=x+1与x轴、y轴分别交于点C、E,∴C(﹣2,0),E(0,1),
设直线BC的解析式为y=kx+b,根据题意得,解得,
∴直线BC的解析式为y=2x+4;∵A(4,0),B(0,4),
设直线AB的解析式为y=ax+4,∴4a+4=0,解得a=﹣1,
∴直线AB的解析式为y=﹣x+4,
∵直线y=x+1与线AB交于点D.
联立得,解得,∴D(2,2);
(2)过点D作DH⊥x轴于H,
∵D(2,2),E(0,1),A(4,0),
∴DH=2,OH=2,OE=1,OA=4,AH=4﹣2=2,
∴S四边形OADE=S梯形OHDE+S△ADH=×2×(1+2)+×2×2=5;
(3)∵F是OA的中点,A(4,0),∴F(2,0),∴AF=OF=2,
设直线l与四边形OADE的另一交点为M,M的纵坐标为y,直线l恰好将四边形OADE分成面积比为1:4的两部分,即直线MF恰好将四边形OADE分成面积比为1:4的两部分,
分两种情况:
①当点M在点F右侧时,S△AMF:S五边形OFMDE=1:4,如图:
∵S四边形OADE=5,∴S△AMF=1,∴AF y=1,即×2y=1,解得y=1,
∵点M在直线AB:y=﹣x+4上,
∴1=﹣x+4,解得x=3,∴点M(3,1),
由F,M两点坐标可求得直线FM的解析式为y=x﹣2,即直线l的解析式为y=x﹣2;
②当点M在点F右左侧时,S△OMF:S五边形MFADE=1:4,如图:
∵S四边形OADE=5,∴S△OMF=1,
∴AF y=1,即×2y=1,解得y=1,∴点M与点E重合,∴点M(0,1),
由F,M两点坐标可求得直线FM的解析式为y=﹣x+1,即直线l的解析式为y=﹣x+1;
综上可知,直线l的解析式为y=x﹣1或y=﹣x+1.
每日一题45参考答案
45.解:(1)如图1,作CE⊥OA于点E,BF⊥OA于F,
∴∠CEO=∠BFA=90°,
∴CE∥BF,且OA∥BC,
∴四边形ECBF是平行四边形,
∴CE=BF,
在Rt△OEC和Rt△AFB中,
,
∴Rt△OEC≌Rt△AFB(HL),
∴OE=AF,
∵A(8,0),B(6,6),
∴0A=8,OF=6,BF=6,
∴OE=2
∴C(2,6),
设直线AC解析式为:y=kx+b(k≠0),
∵直线AC过点A(8,0),C(2,6),
∴,解得,
∴直线AC解析式为y=﹣x+8;
(2)∵直线AC解析式为y=﹣x+8,
∴D(0,8),
∵A(8,0),C(2,6),
∴OD=OA=8,
∴S△OAD=×8×2=8,S△OAC=×8×6=24,
设P点坐标(x,﹣x+8),分两种情况:
①点P在点C的左侧,
∵S△OCP=S△OCD+S△ODP=12,
∴S△ODP=12﹣8=4,
∴×8×(﹣x)=4;解得:x=﹣1,
∴P点坐标(﹣1,9);
②点P在点C的右侧,
∴S△OCP=12,S△OAC=24,
∴点P是AC的中点,
∵A(8,0),C(2,6),
∴P点坐标(5,3);
综上,P点坐标为(﹣1,9)或(5,3);
(3)在y轴右侧的直线AC上存在一点M点,使得△OCM为等腰三角形,
设M(m,﹣m+8),
分三种情况:
①OC=CM,如图,过点M作MN⊥OA于N,
∵A(8,0),C(2,6),
∴OC=CM==2,AC==6,
∴AM=6﹣2,
∵A(8,0),D(0,8),
∴OA=OD=8,
∴∠OAD=45°,
∴MN=NA==6﹣2,
∴ON=8﹣(6﹣2)=2+2,
∴M(2+2,6﹣2);
②OM=CM;如图,过点M作MN⊥OA于N,
∴OM2=ON2+MN2.
∴OM2=m2+(﹣m+8)2=2m2﹣16m+64,
∵∠OAD=45°,
∴MN=NA=﹣m+8,AM=(﹣m+8),
∴CM=AC﹣AM=6﹣(﹣m+8)=m﹣8,
∴CM2=(m﹣8)2=2m2﹣8m+8,
∵OM=CM,
∴2m2﹣16m+64=2m2﹣8m+8,解得:m=7,
∴M(7,1);
③OC=OM,如图,过点M作MN⊥OA于N,
∴OM=OC==2,
∴OM2=m2+(﹣m+8)2=2m2﹣16m+64=40,
∴2m2﹣16m+64=40,解得:m=6或2,
∵m=2时点M与点C重合,故舍去,
∴M(6,2).
综上可知,在y轴右侧的直线AC上存在一点M点,使得△OCM为等腰三角形,M点的坐标为(2+2,6﹣2)或(7,1)或(6,2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题41
班级 姓名 小组
41.如图,在△ABC中,点M为BC边上的中点,连接AM,D是线段AM上一点(不与点A重合).过点D作DE∥AB,过点C作CE∥AM,连接AE.
(1)如图1,当点D与M重合时,求证:
①△ABD≌△EDC.
②四边形ABDE是平行四边形.
(2)如图2,延长BD交AC于点H,若BH⊥AC,且BH=AM,求∠CAM的度数.
每日一题42
班级 姓名 小组
42.如图,一次函数的图象经过点A(4,0),B(0,3).以线段AB为边在第一象限内作等腰直角三角形ABC,∠BAC=90°.若第二象限内有一点P(a,),且△ABP的面积与△ABC的面积相等.
(1)求直线AB的函数表达式.
(2)求a的值.
(3)在x轴上是否存在点M,使△MAC为等腰三角形,若存在,直接写出点M的坐标;若不存在.请说明理由.
每日一题43
班级 姓名 小组
43.如图1,D是等边三角形ABC内一点,DB=DC,∠BDC=90°,连接AD.
(1)求∠BAD的度数;
(2)如图2,以AB为斜边在△ABC外作等腰直角△ABE,连接DE.
①请判断△ADE的形状,并说明理由;
②若BC=4,求点E到AD的距离.
每日一题44
班级 姓名 小组
44.如图,A(4,0),B(0,4),直线y=x+1与x轴、y轴、直线AB分别交于点C、E、D.
(1)求直线BC的解析式及D点的坐标;
(2)求四边形OADE的面积;
(3)F是OA的中点,过点F作直线l,若l恰好将四边形OADE分成面积比为1:4的两部分,求直线l的解析式.
每日一题45
班级 姓名 小组
45.在等腰梯形OABC中,OA∥BC,AB=OC,在建立如图的平面直角坐标系中,A(8,0),B(6,6),直线AC与y轴交于点D.
(1)直接写出C点的坐标,并求出直线AC的解析式;
(2)点P的直线AC上,且△OCP的面积为12,请求出点P的坐标.
(3)在y轴右侧的直线AC上是否存在一点M点,使得△OCM为等腰三角形?若有,请求出M点的坐标,若没有,请说明理由.
每日一题41参考答案
41.(1)①如图1中,
∵DE∥AB,
∴∠EDC=∠ABM,
∵CE∥AM,
∴∠ECD=∠ADB,
∵AM是△ABC的中线,且D与M重合,
∴BD=DC,
在△ABD与△EDC中,
,
∴△ABD≌△EDC(ASA).
②由①得△ABD≌△EDC,
∴AB=ED,
∵AB∥ED,
∴四边形ABDE是平行四边形.
(2)如图2中,取线段HC的中点I,连接MI,
∵BM=MC,
∴MI是△BHC的中位线,
∴MI∥BH,,
∵BH⊥AC,且.
∴,MI⊥AC,
∴∠CAM=45°.
每日一题42参考答案
42.解:(1)设直线AB的解析式为y=kx+b(k≠0),
将点A(4,0),B(0,3)代入解析式,
得,解得,∴直线AB的解析式为y=﹣x+3;
(2)如图,过点P作PD⊥x轴交于点D,∵A(4,0),B(0,3),∴OA=4,OB=3,
∵等腰直角三角形ABC,∠BAC=90°,由勾股定理可得AB=AC=5,
∵P(a,),∴PD=,OD=﹣a,
S△ABP=S梯形PDOB+S△ABO﹣S△APD=(OB+PD)×OD+×OA×OB﹣×PD×AD=(3+)×(﹣a)+×3×4﹣××(4﹣a)=﹣a+,
S△ABC=×AB×AC=,
∵△ABP的面积与△ABC的面积相等,∴﹣a+=,∴a=﹣5;
(3)①当AC=CM时,过C点作CE⊥x轴交于点E,
∵∠BOA=∠AEC=90°,∠BAC=90°,∴∠BAO=∠ACE,
∵AB=AC,∴△ABO≌△CAE(AAS),
∴AE=BO,∵BO=3,∴AE=3,
∵AE是等腰三角形ACM边AM的中点,∴AM=6,∴M(10,0);
②当AC=AM时,∵AC=5,∴AM=5,∴M(9,0)或M(﹣1,0);
③当CM=AM时,作AC的垂线平分线HM,分别交AC、x轴于点H、M,∵AC=5,∴AH=,
∵∠BOA=∠AHM=90°,∴∠OBA=∠HAM,
∴cos∠OBA=cos∠HAM,即==,∴AM=,
∴MO=4+=,∴M(,0);
综上所述:△MAC为等腰三角形时,M点的坐标为(10,0)或(9,0)或(,0)或(﹣1,0).
每日一题43参考答案
43.解:(1)∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,AB=BC=AC,
在△ADB和△ADC中,,
∴△ADB≌△ADC(SSS),
∴∠BAD=∠CAD=∠BAC=×60°=30°;
(2)①△ADE是等腰三角形,理由如下:
∵DB=DC,∠BDC=90°,
∴△CBD是以BC为斜边的等腰直角三角形,∠DBC=45°,
∵以AB为斜边在△ABC外作等腰直角△ABE,AB=BC,
∴∠EBA=45°,AE=BE=DB=DC,
∴∠EBA+∠ABD=∠ABD+∠DBC=∠ABC=60°,即∠EBD=60°,
∴△BDE是等边三角形,∴DE=BE,∴AE=DE,∴△ADE是等腰三角形;
②延长AD交BC于点F,过点E作EN⊥AD于N,如图2所示:
∵∠BAD=∠CAD,
∴AF是∠BAC的平分线,AF⊥BC,BF=BC=2,
∵∠DBC=45°,
∴△BDF是等腰直角三角形,
∴DF=BF=2,
AF===2,
∴AD=AF﹣DF=2﹣2,
∵△ADE是等腰三角形,
∴DN=AN=AD=﹣1,
∵DE=BD=BF=2,
∴EN===1+,
∴点E到AD的距离为1+.
每日一题44 参考答案
44.解:(1)∵直线y=x+1与x轴、y轴分别交于点C、E,∴C(﹣2,0),E(0,1),
设直线BC的解析式为y=kx+b,根据题意得,解得,
∴直线BC的解析式为y=2x+4;∵A(4,0),B(0,4),
设直线AB的解析式为y=ax+4,∴4a+4=0,解得a=﹣1,
∴直线AB的解析式为y=﹣x+4,
∵直线y=x+1与线AB交于点D.
联立得,解得,∴D(2,2);
(2)过点D作DH⊥x轴于H,
∵D(2,2),E(0,1),A(4,0),
∴DH=2,OH=2,OE=1,OA=4,AH=4﹣2=2,
∴S四边形OADE=S梯形OHDE+S△ADH=×2×(1+2)+×2×2=5;
(3)∵F是OA的中点,A(4,0),∴F(2,0),∴AF=OF=2,
设直线l与四边形OADE的另一交点为M,M的纵坐标为y,直线l恰好将四边形OADE分成面积比为1:4的两部分,即直线MF恰好将四边形OADE分成面积比为1:4的两部分,
分两种情况:
①当点M在点F右侧时,S△AMF:S五边形OFMDE=1:4,如图:
∵S四边形OADE=5,∴S△AMF=1,∴AF y=1,即×2y=1,解得y=1,
∵点M在直线AB:y=﹣x+4上,
∴1=﹣x+4,解得x=3,∴点M(3,1),
由F,M两点坐标可求得直线FM的解析式为y=x﹣2,即直线l的解析式为y=x﹣2;
②当点M在点F右左侧时,S△OMF:S五边形MFADE=1:4,如图:
∵S四边形OADE=5,∴S△OMF=1,
∴AF y=1,即×2y=1,解得y=1,∴点M与点E重合,∴点M(0,1),
由F,M两点坐标可求得直线FM的解析式为y=﹣x+1,即直线l的解析式为y=﹣x+1;
综上可知,直线l的解析式为y=x﹣1或y=﹣x+1.
每日一题45参考答案
45.解:(1)如图1,作CE⊥OA于点E,BF⊥OA于F,
∴∠CEO=∠BFA=90°,
∴CE∥BF,且OA∥BC,
∴四边形ECBF是平行四边形,
∴CE=BF,
在Rt△OEC和Rt△AFB中,
,
∴Rt△OEC≌Rt△AFB(HL),
∴OE=AF,
∵A(8,0),B(6,6),
∴0A=8,OF=6,BF=6,
∴OE=2
∴C(2,6),
设直线AC解析式为:y=kx+b(k≠0),
∵直线AC过点A(8,0),C(2,6),
∴,解得,
∴直线AC解析式为y=﹣x+8;
(2)∵直线AC解析式为y=﹣x+8,
∴D(0,8),
∵A(8,0),C(2,6),
∴OD=OA=8,
∴S△OAD=×8×2=8,S△OAC=×8×6=24,
设P点坐标(x,﹣x+8),分两种情况:
①点P在点C的左侧,
∵S△OCP=S△OCD+S△ODP=12,
∴S△ODP=12﹣8=4,
∴×8×(﹣x)=4;解得:x=﹣1,
∴P点坐标(﹣1,9);
②点P在点C的右侧,
∴S△OCP=12,S△OAC=24,
∴点P是AC的中点,
∵A(8,0),C(2,6),
∴P点坐标(5,3);
综上,P点坐标为(﹣1,9)或(5,3);
(3)在y轴右侧的直线AC上存在一点M点,使得△OCM为等腰三角形,
设M(m,﹣m+8),
分三种情况:
①OC=CM,如图,过点M作MN⊥OA于N,
∵A(8,0),C(2,6),
∴OC=CM==2,AC==6,
∴AM=6﹣2,
∵A(8,0),D(0,8),
∴OA=OD=8,
∴∠OAD=45°,
∴MN=NA==6﹣2,
∴ON=8﹣(6﹣2)=2+2,
∴M(2+2,6﹣2);
②OM=CM;如图,过点M作MN⊥OA于N,
∴OM2=ON2+MN2.
∴OM2=m2+(﹣m+8)2=2m2﹣16m+64,
∵∠OAD=45°,
∴MN=NA=﹣m+8,AM=(﹣m+8),
∴CM=AC﹣AM=6﹣(﹣m+8)=m﹣8,
∴CM2=(m﹣8)2=2m2﹣8m+8,
∵OM=CM,
∴2m2﹣16m+64=2m2﹣8m+8,解得:m=7,
∴M(7,1);
③OC=OM,如图,过点M作MN⊥OA于N,
∴OM=OC==2,
∴OM2=m2+(﹣m+8)2=2m2﹣16m+64=40,
∴2m2﹣16m+64=40,解得:m=6或2,
∵m=2时点M与点C重合,故舍去,
∴M(6,2).
综上可知,在y轴右侧的直线AC上存在一点M点,使得△OCM为等腰三角形,M点的坐标为(2+2,6﹣2)或(7,1)或(6,2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
