浙教版八年级上册数学每日一题46-50(第5章 一次函数)培优练习(含答案)
文档属性
| 名称 | 浙教版八年级上册数学每日一题46-50(第5章 一次函数)培优练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 13:53:36 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
每日一题46
班级 姓名 小组
46.如图,在平面直角坐标系xOy中,直线y=kx+4与x轴、y轴分别交于A、B两点,4OA=3OB.
(1)求k的值;
(2)点P在线段AB上,连接OP.若S△AOB=3S△BOP,求点P的坐标;
(3)将直线AB绕点A逆时针旋转45°后得到直线AC,求直线AC的表达式.
每日一题47
班级 姓名 小组
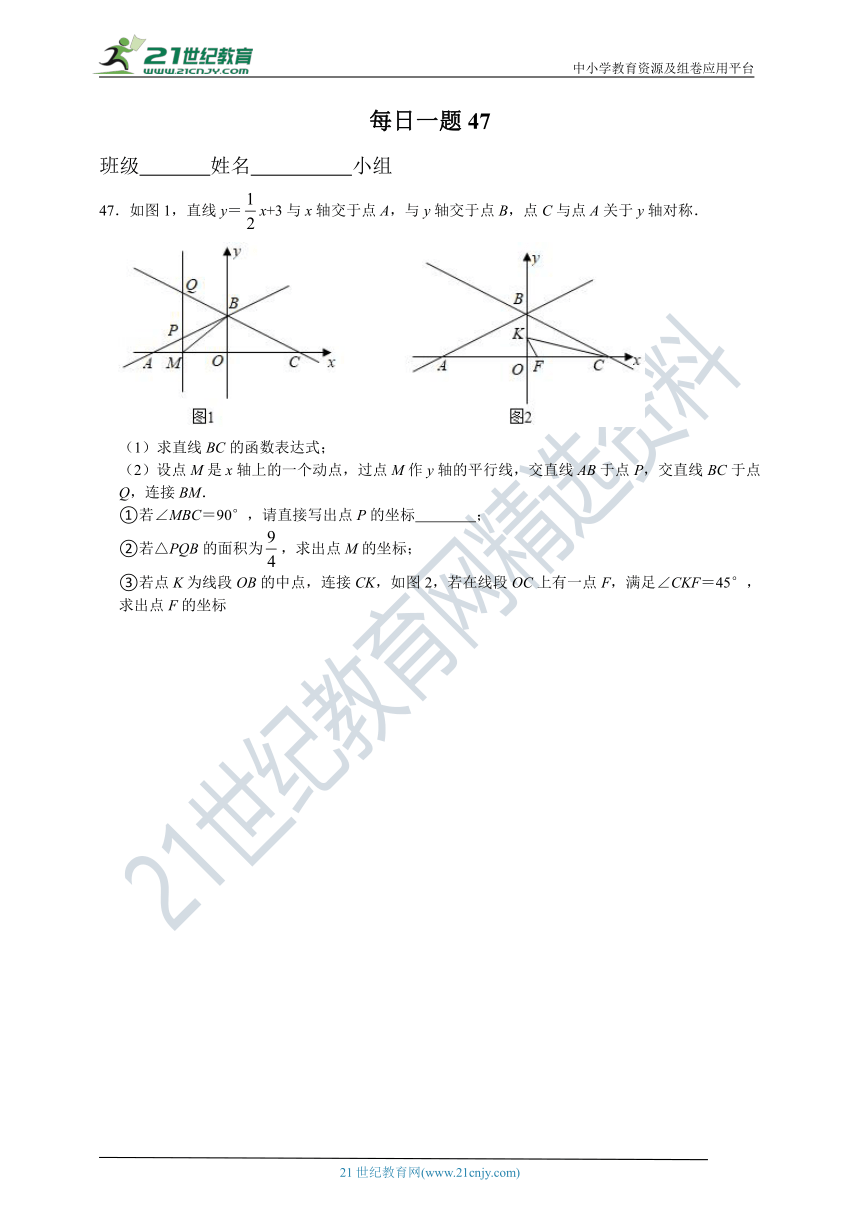
47.如图1,直线y=x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数表达式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,请直接写出点P的坐标 ;
②若△PQB的面积为,求出点M的坐标;
③若点K为线段OB的中点,连接CK,如图2,若在线段OC上有一点F,满足∠CKF=45°,求出点F的坐标
每日一题48
班级 姓名 小组
48.【模型建立】
(1)如图1,等腰Rt△ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E,求证:△BEC≌△CDA;
【模型应用】
(2)如图2,已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,将直线l1绕点A逆时针旋转45°至直线l2;求直线l2的函数表达式;
(3)如图3,平面直角坐标系内有一点B(3,﹣4),过点B作BA⊥x轴于点A、BC⊥y轴于点C,点P是线段AB上的动点,点D是直线y=﹣2x+1上的动点且在第四象限内.试探究△CPD能否成为等腰直角三角形?若能,求出点D的坐标,若不能,请说明理由.
每日一题49
班级 姓名 小组
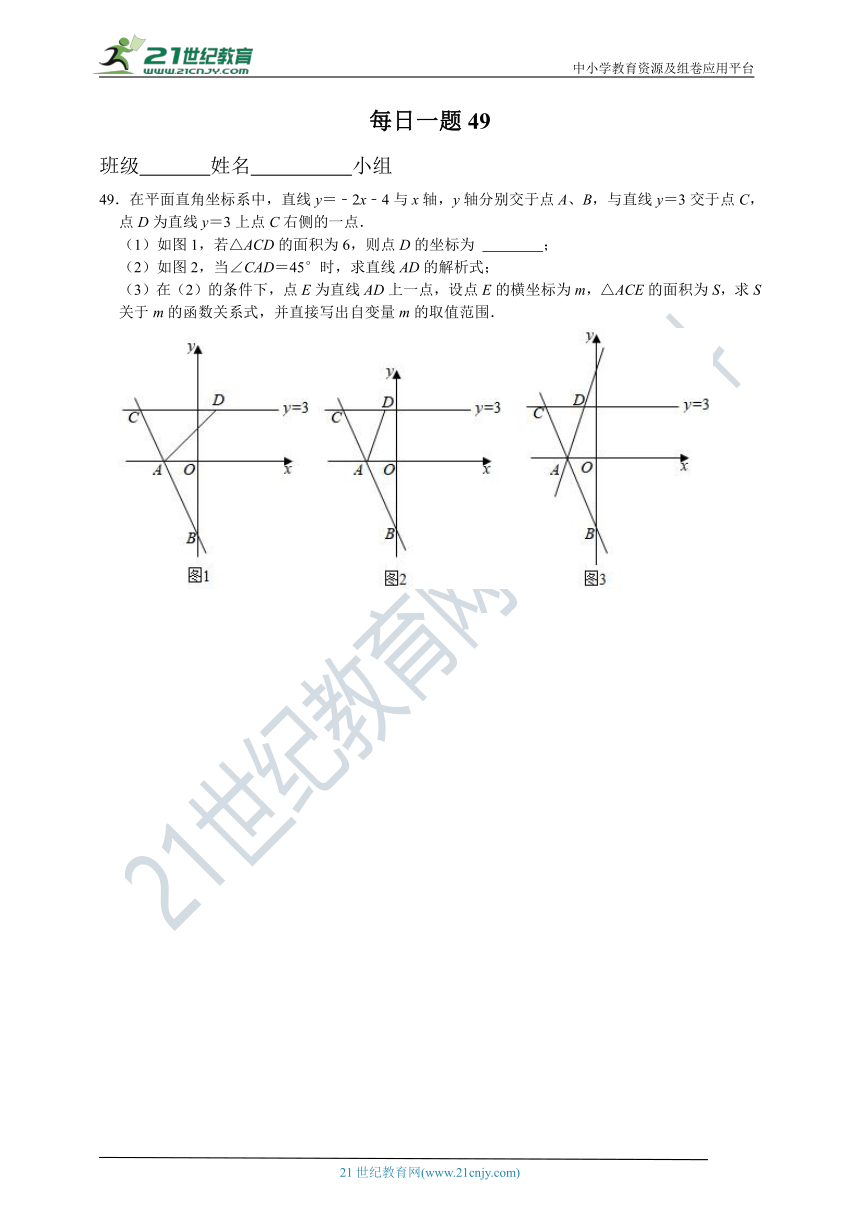
49.在平面直角坐标系中,直线y=﹣2x﹣4与x轴,y轴分别交于点A、B,与直线y=3交于点C,点D为直线y=3上点C右侧的一点.
(1)如图1,若△ACD的面积为6,则点D的坐标为 ;
(2)如图2,当∠CAD=45°时,求直线AD的解析式;
(3)在(2)的条件下,点E为直线AD上一点,设点E的横坐标为m,△ACE的面积为S,求S关于m的函数关系式,并直接写出自变量m的取值范围.
每日一题50
班级 姓名 小组
50.已知,如图,直线y=kx+b分别与y轴,x轴交于点A(0,8)和点B(4,0),点M(2,m)是AB上一点,直线y=﹣x沿x轴作平移运动,平移时交OA于点D,交OB于点C.
(1)求m的值;
(2)如图1,当直线y=﹣x从点O出发以1单位长度/s的速度匀速沿x轴正方向平移,平移到达点B时结束运动,过点D作DE⊥y轴交AB于点E,连接CE,设运动时间为t(s).是否存在t值,使得△CDE是以CD为腰的等腰三角形?如果能,请求出相应的t值;如果不能,请说明理由;
(3)如图2,连接MC,将MC绕点M顺时针旋转90°得到MN,连接AN,请求出AN+MN的最小值.
每日一题46参考答案
解:(1)直线y=kx+4中,令x=0,则y=4,
∴B(0,4),∴OB=4,
∵4OA=3OB,∴OA=3,
由图可知点A在x轴的正半轴,
∴A(3,0),∴3k+4=0,∴k=.
(2)由(1)知OA=3,OB=4,y=x+4,∴S△AOB= OA OB=×3×4=6,
∵S△AOB=3S△BOP,∴S△BOP=S△AOB=2.
过点P作PM⊥y轴于点M,∴S△BOP= OB PM=2,即×4PM=2,
∴PM=1,即点P的横坐标为1,
当x=1时,y=﹣×1+4=;∴点P的坐标为(1,).
(3)将直线AB绕点A逆时针旋转45°后得到直线AC,则∠BAC=45°,如图,过点B作BD⊥AB交直线AC于点D,过点D作DE⊥y轴于点E,
∴∠BED=∠AOB=90°,
∴∠ABO+∠OBD=∠BDE+∠OBE=90°,
∴∠ABO=∠BDE,
∵∠BAC=45°,∴∠BDA=45°,
∴BD=AB,∴△BDE≌△ABO(AAS),
∴BE=OA=3,DE=OB=4,
∴OE=OB﹣BE=1,
∴D(﹣4,1),
设直线AC的解析式为:y=mx+n,
∴,解得,∴直线AC的表达式为:y=﹣x+.
每日一题47参考答案
47.解:(1)对于,令x=0,y=3,∴B(0,3),
令y=0,∴,∴x=﹣6,∴A(﹣6,0),
∵点C与点A关于y轴对称,∴C(6,0),
设直线BC的解析式为y=kx+b,
∴,∴,∴直线BC的解析式为,
(2)①设点M(m,0),∴,
∵B(0,3),C(6,0),∴BC2=45,BM2=OM2+OB2=m2+9,MC2=(6﹣m)2,
∵∠MBC=90°,∴△BMC是直角三角形,∴BM2+BC2=MC2,
∴m2+9+45=(6﹣m)2,∴,∴,,故答案为:,.
②设点M(n,0),∵点P在直线上,∴,
∵点Q在直线上,∴,∴,
∵△PQB的面积为,∴,∴,
∴,0)或,0),
③过点F作FH⊥FK交CK于H,过点H作HE⊥x轴于E,
∵∠CKF=45°,∴△KFH是等腰直角三角形,
∴KF=FH,∠KFO+∠HFE=90°,
∵∠KFO+∠FKO=90°,∴∠HFE=∠FKO,
∵∠KOF=∠FEH=90°,∴△KOF≌△FEH(AAS),
∴EH=OF,EF=OK,
∵点K为线段OB的中点,OB=6,∴,,
设F(x,0),则,EH=OF=x,则,x),
∵C(6,0),,设直线CK的解析式为y=kx+b,
∴,解得:,∴直线CK的解析式为,
∵点H在CK上,,x),∴,解得:,∴点F的坐标为,0).
每日一题48参考答案
48.解:(1)如图1所示:
∵AD⊥ED,BE⊥ED,∴∠ADC=∠CEB=90°,
又∵∠ACD+∠ACB+∠BEC=180°,∠ACB=90°,
∴∠ACD+∠BEC=90°,又∵∠ACD+∠DAC=90°,
∴∠DAC=∠ECB,
在△CDA和△BEC中,
,∴△CDA≌△BEC(AAS);
(2)过点B作BC⊥AB交AC于点C,CD⊥y轴交y轴于点D,如图2所示:
∵CD⊥y轴,x轴⊥y轴,∴∠CDB=∠BOA=90°,
又∵BC⊥AB,∴∠ABC=90°,
又∵∠ABO+∠ABC+∠CBD=180°,∴∠ABO+∠CBD=90°,
又∵∠BAO+∠ABO=90°,∴∠BAO=∠CBD,
又∵∠BAC=45°,∴∠ACB=45°,∴AB=CB,
在△ABO和∠BCD中,
,∴△ABO≌∠BCD(AAS),∴AO=BD,BO=CD,
又∵直线l1:y=x+3与x轴交于点A,与y轴交于点B,
∴点A、B两点的坐标分别为(﹣2,0),(0,3),∴AO=2,BO=3,∴BD=2,CD=3,
∴点C的坐标为(﹣3,5),
设l2的函数表达式为y=kx+b(k≠0),
点A、C两点在直线l2上,依题意得:
,解得:,∴直线l2的函数表达式为y=﹣5x﹣10;
(3)能成为等腰直角三角形,依题意得,
①若点P为直角时,如图3甲所示:
设点P的坐标为(3,m),则PB的长为4+m,
∵∠CPD=90°,CP=PD,∠CPM+∠CDP+∠PDH=180°,
∴∠CPM+∠PDH=90°,又∵∠CPM+∠DPM=90°,∴∠PCM=∠PDH,
在△MCP和△HPD中,
,∴△MCP≌△HPD(AAS),∴CM=PH,PM=PD,
∴点D的坐标为(7+m,﹣3+m),
又∵点D在直线y=﹣2x+1上,∴﹣2(7+m)+1=﹣3+m,
解得:m=﹣,即点D的坐标为(,﹣);
②若点C为直角时,如图3乙所示:
设点P的坐标为(3,n),则PB的长为4+n,CA=CD,
同理可证明△PCM≌△CDH(AAS),
∴PM=CH,MC=HD,∴点D的坐标为(4+n,﹣7),
又∵点D在直线y=﹣2x+1上,∴﹣2(4+n)+1=﹣7,解得:n=0,
∴点P与点A重合,点M与点O重合,即点D的坐标为(4,﹣7);
③若点D为直角时,如图3丙所示:
设点P的坐标为(3,k),则PB的长为4+k,CD=PD,
同理可证明△CDM≌△PDQ(AAS),∴MD=PQ,MC=DQ,
∴点D的坐标为(,),又∵点D在直线y=﹣2x+1上,
∴﹣2×=,解得:k=,
∴点P与点A重合,点M与点O重合,
即点D的坐标为(,﹣);
综合所述,点D的坐标为(,﹣)或(4,﹣7)或(,﹣).
每日一题49 参考答案
49.解:(1)如图1,对于直线y=﹣2x﹣4,当y=0时,由﹣2x﹣4=0得,x=﹣2,
∴A(﹣2,0);当y=3时,由﹣2x﹣4=3得,x=﹣,∴C(﹣,3),
设D(r,3),∵点D在点C右侧,∴CD=r+,
由题意,得×3(r+)=6,解得,r=,
∴D(,3),故答案为:D(,3).
(2)如图2,过点D作DG⊥AC于点G,过点G作MN⊥x轴于点N,交直线y=3于点M,则∠AGD=∠GNA=90°,
∵直线y=3与x轴平行,∴∠DMG=180°﹣∠GNA=90°=∠GNA,
∵∠GAD=45°,∴∠GDA=45°=∠GAD,∴DG=GA,
∵∠DGM=90°﹣∠AGN=∠GAN,∴△DGM≌△GAN(AAS),
∴GM=AN,DM=GN,
设AN=t,则N(﹣2﹣t,0),∵点G在直线y=﹣2x﹣4上,∴yG=﹣2(﹣2﹣t)﹣4=2t,
∴G(﹣2﹣t,2t),∵M(﹣2﹣t,3),∴GM=3﹣2t,
由GM=AN得,3﹣2t=t,解得t=1,∴N(﹣3,0),M(﹣3,3),
∵DM=GN=2t=2,∴D(﹣1,3),
设直线AD的解析式为y=kx+b,
则,解得,∴y=3x+6.
(3)由(1)、(2)得,C(﹣,3),D(﹣1,3),∴CD=﹣1﹣(﹣)=,
∴S△ACD=××3=,
过点E作直线y=3的垂线,垂足为点F,
∵点E在直线y=3x+6上,且点E的横坐标为m,∴E(m,3m+6),
如图3,点E在线段AD上,则﹣2<m≤﹣1,
此时,EF=3﹣(3m+6)=﹣3m﹣3,
由S△ACE=S△ACD﹣S△ECD得,
S=﹣×(﹣3m﹣3)=m+;
如图4,点E在线段AD的延长线上,则m>﹣1,
此时,EF=3m+6﹣3=3m+3,
由S△ACE=S△ACD+S△ECD得,
S=+×(3m+3)=m+,
∴当m>﹣2时,S=m+;
如图5,点E在线段DA的延长线上,则m<﹣2,
此时,EF=3﹣(3m+6)=﹣3m﹣3,
由S△ACE=S△ECD﹣S△ACD得,
S=×(﹣3m﹣3)﹣=﹣m﹣,
综上所述,.
每日一题50参考答案
50.解:(1)由直线y=kx+b分别与x轴、y轴交于点A(0,8)、B(4,0)得,
,解得,∴y=﹣2x+8,
∵点M(2,m)在y=﹣2x+8上,∴m=﹣2×2+8=4.
(2)存在.如图1,连接BD,∵AD OB=AD DE+OD DE=S△ABD,
∴4AD=(AD+OD)DE=8DE,∴AD=2DE;
当CE=CD时,作CF⊥DE于点F,则DF=EF,
设直线CD的解析式为y=﹣x+n,
∵C(t,0),∴﹣t+n=0,解得n=t,∴y=﹣x+t,∴D(0,t),∴F(t,t),
∴DE=2DF=2t,∴8﹣t=2×2t,解得,t=;
当ED=CD时,如图2,
∵∠COD=90°,OC=OD=t,∴CD==t,∴8﹣t=2×t,
解得,t=,综上所述,t=或t=.
(3)如图3,过点M作MH⊥OB于点H,作NG⊥MH交HM的延长线于点G,
∵∠G=∠MHC=90°,∠CMN=90°,∴∠GNM=90°﹣∠GMN=∠HMC,
∵MN=CM,∴△MNG≌△CMH(AAS),
由(1)得,M(2,4),∴GN=HM=4,
∵2﹣4=﹣2,∴点N的横坐标为﹣2,∴点N在直线l:x=﹣2上运动;
作点A关于直线l的对称点A′,连接MA′交直线l于点N′,则A′(﹣4,8),
当点N接近点N′时,AN+MN的值最小,此时点C与点O重合,
∴MG=CH=2,∴N(﹣2,6),
∴AN+MN=+=2+2,
AN+MN的最小值为2+2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题46
班级 姓名 小组
46.如图,在平面直角坐标系xOy中,直线y=kx+4与x轴、y轴分别交于A、B两点,4OA=3OB.
(1)求k的值;
(2)点P在线段AB上,连接OP.若S△AOB=3S△BOP,求点P的坐标;
(3)将直线AB绕点A逆时针旋转45°后得到直线AC,求直线AC的表达式.
每日一题47
班级 姓名 小组
47.如图1,直线y=x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数表达式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,请直接写出点P的坐标 ;
②若△PQB的面积为,求出点M的坐标;
③若点K为线段OB的中点,连接CK,如图2,若在线段OC上有一点F,满足∠CKF=45°,求出点F的坐标
每日一题48
班级 姓名 小组
48.【模型建立】
(1)如图1,等腰Rt△ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E,求证:△BEC≌△CDA;
【模型应用】
(2)如图2,已知直线l1:y=x+3与x轴交于点A,与y轴交于点B,将直线l1绕点A逆时针旋转45°至直线l2;求直线l2的函数表达式;
(3)如图3,平面直角坐标系内有一点B(3,﹣4),过点B作BA⊥x轴于点A、BC⊥y轴于点C,点P是线段AB上的动点,点D是直线y=﹣2x+1上的动点且在第四象限内.试探究△CPD能否成为等腰直角三角形?若能,求出点D的坐标,若不能,请说明理由.
每日一题49
班级 姓名 小组
49.在平面直角坐标系中,直线y=﹣2x﹣4与x轴,y轴分别交于点A、B,与直线y=3交于点C,点D为直线y=3上点C右侧的一点.
(1)如图1,若△ACD的面积为6,则点D的坐标为 ;
(2)如图2,当∠CAD=45°时,求直线AD的解析式;
(3)在(2)的条件下,点E为直线AD上一点,设点E的横坐标为m,△ACE的面积为S,求S关于m的函数关系式,并直接写出自变量m的取值范围.
每日一题50
班级 姓名 小组
50.已知,如图,直线y=kx+b分别与y轴,x轴交于点A(0,8)和点B(4,0),点M(2,m)是AB上一点,直线y=﹣x沿x轴作平移运动,平移时交OA于点D,交OB于点C.
(1)求m的值;
(2)如图1,当直线y=﹣x从点O出发以1单位长度/s的速度匀速沿x轴正方向平移,平移到达点B时结束运动,过点D作DE⊥y轴交AB于点E,连接CE,设运动时间为t(s).是否存在t值,使得△CDE是以CD为腰的等腰三角形?如果能,请求出相应的t值;如果不能,请说明理由;
(3)如图2,连接MC,将MC绕点M顺时针旋转90°得到MN,连接AN,请求出AN+MN的最小值.
每日一题46参考答案
解:(1)直线y=kx+4中,令x=0,则y=4,
∴B(0,4),∴OB=4,
∵4OA=3OB,∴OA=3,
由图可知点A在x轴的正半轴,
∴A(3,0),∴3k+4=0,∴k=.
(2)由(1)知OA=3,OB=4,y=x+4,∴S△AOB= OA OB=×3×4=6,
∵S△AOB=3S△BOP,∴S△BOP=S△AOB=2.
过点P作PM⊥y轴于点M,∴S△BOP= OB PM=2,即×4PM=2,
∴PM=1,即点P的横坐标为1,
当x=1时,y=﹣×1+4=;∴点P的坐标为(1,).
(3)将直线AB绕点A逆时针旋转45°后得到直线AC,则∠BAC=45°,如图,过点B作BD⊥AB交直线AC于点D,过点D作DE⊥y轴于点E,
∴∠BED=∠AOB=90°,
∴∠ABO+∠OBD=∠BDE+∠OBE=90°,
∴∠ABO=∠BDE,
∵∠BAC=45°,∴∠BDA=45°,
∴BD=AB,∴△BDE≌△ABO(AAS),
∴BE=OA=3,DE=OB=4,
∴OE=OB﹣BE=1,
∴D(﹣4,1),
设直线AC的解析式为:y=mx+n,
∴,解得,∴直线AC的表达式为:y=﹣x+.
每日一题47参考答案
47.解:(1)对于,令x=0,y=3,∴B(0,3),
令y=0,∴,∴x=﹣6,∴A(﹣6,0),
∵点C与点A关于y轴对称,∴C(6,0),
设直线BC的解析式为y=kx+b,
∴,∴,∴直线BC的解析式为,
(2)①设点M(m,0),∴,
∵B(0,3),C(6,0),∴BC2=45,BM2=OM2+OB2=m2+9,MC2=(6﹣m)2,
∵∠MBC=90°,∴△BMC是直角三角形,∴BM2+BC2=MC2,
∴m2+9+45=(6﹣m)2,∴,∴,,故答案为:,.
②设点M(n,0),∵点P在直线上,∴,
∵点Q在直线上,∴,∴,
∵△PQB的面积为,∴,∴,
∴,0)或,0),
③过点F作FH⊥FK交CK于H,过点H作HE⊥x轴于E,
∵∠CKF=45°,∴△KFH是等腰直角三角形,
∴KF=FH,∠KFO+∠HFE=90°,
∵∠KFO+∠FKO=90°,∴∠HFE=∠FKO,
∵∠KOF=∠FEH=90°,∴△KOF≌△FEH(AAS),
∴EH=OF,EF=OK,
∵点K为线段OB的中点,OB=6,∴,,
设F(x,0),则,EH=OF=x,则,x),
∵C(6,0),,设直线CK的解析式为y=kx+b,
∴,解得:,∴直线CK的解析式为,
∵点H在CK上,,x),∴,解得:,∴点F的坐标为,0).
每日一题48参考答案
48.解:(1)如图1所示:
∵AD⊥ED,BE⊥ED,∴∠ADC=∠CEB=90°,
又∵∠ACD+∠ACB+∠BEC=180°,∠ACB=90°,
∴∠ACD+∠BEC=90°,又∵∠ACD+∠DAC=90°,
∴∠DAC=∠ECB,
在△CDA和△BEC中,
,∴△CDA≌△BEC(AAS);
(2)过点B作BC⊥AB交AC于点C,CD⊥y轴交y轴于点D,如图2所示:
∵CD⊥y轴,x轴⊥y轴,∴∠CDB=∠BOA=90°,
又∵BC⊥AB,∴∠ABC=90°,
又∵∠ABO+∠ABC+∠CBD=180°,∴∠ABO+∠CBD=90°,
又∵∠BAO+∠ABO=90°,∴∠BAO=∠CBD,
又∵∠BAC=45°,∴∠ACB=45°,∴AB=CB,
在△ABO和∠BCD中,
,∴△ABO≌∠BCD(AAS),∴AO=BD,BO=CD,
又∵直线l1:y=x+3与x轴交于点A,与y轴交于点B,
∴点A、B两点的坐标分别为(﹣2,0),(0,3),∴AO=2,BO=3,∴BD=2,CD=3,
∴点C的坐标为(﹣3,5),
设l2的函数表达式为y=kx+b(k≠0),
点A、C两点在直线l2上,依题意得:
,解得:,∴直线l2的函数表达式为y=﹣5x﹣10;
(3)能成为等腰直角三角形,依题意得,
①若点P为直角时,如图3甲所示:
设点P的坐标为(3,m),则PB的长为4+m,
∵∠CPD=90°,CP=PD,∠CPM+∠CDP+∠PDH=180°,
∴∠CPM+∠PDH=90°,又∵∠CPM+∠DPM=90°,∴∠PCM=∠PDH,
在△MCP和△HPD中,
,∴△MCP≌△HPD(AAS),∴CM=PH,PM=PD,
∴点D的坐标为(7+m,﹣3+m),
又∵点D在直线y=﹣2x+1上,∴﹣2(7+m)+1=﹣3+m,
解得:m=﹣,即点D的坐标为(,﹣);
②若点C为直角时,如图3乙所示:
设点P的坐标为(3,n),则PB的长为4+n,CA=CD,
同理可证明△PCM≌△CDH(AAS),
∴PM=CH,MC=HD,∴点D的坐标为(4+n,﹣7),
又∵点D在直线y=﹣2x+1上,∴﹣2(4+n)+1=﹣7,解得:n=0,
∴点P与点A重合,点M与点O重合,即点D的坐标为(4,﹣7);
③若点D为直角时,如图3丙所示:
设点P的坐标为(3,k),则PB的长为4+k,CD=PD,
同理可证明△CDM≌△PDQ(AAS),∴MD=PQ,MC=DQ,
∴点D的坐标为(,),又∵点D在直线y=﹣2x+1上,
∴﹣2×=,解得:k=,
∴点P与点A重合,点M与点O重合,
即点D的坐标为(,﹣);
综合所述,点D的坐标为(,﹣)或(4,﹣7)或(,﹣).
每日一题49 参考答案
49.解:(1)如图1,对于直线y=﹣2x﹣4,当y=0时,由﹣2x﹣4=0得,x=﹣2,
∴A(﹣2,0);当y=3时,由﹣2x﹣4=3得,x=﹣,∴C(﹣,3),
设D(r,3),∵点D在点C右侧,∴CD=r+,
由题意,得×3(r+)=6,解得,r=,
∴D(,3),故答案为:D(,3).
(2)如图2,过点D作DG⊥AC于点G,过点G作MN⊥x轴于点N,交直线y=3于点M,则∠AGD=∠GNA=90°,
∵直线y=3与x轴平行,∴∠DMG=180°﹣∠GNA=90°=∠GNA,
∵∠GAD=45°,∴∠GDA=45°=∠GAD,∴DG=GA,
∵∠DGM=90°﹣∠AGN=∠GAN,∴△DGM≌△GAN(AAS),
∴GM=AN,DM=GN,
设AN=t,则N(﹣2﹣t,0),∵点G在直线y=﹣2x﹣4上,∴yG=﹣2(﹣2﹣t)﹣4=2t,
∴G(﹣2﹣t,2t),∵M(﹣2﹣t,3),∴GM=3﹣2t,
由GM=AN得,3﹣2t=t,解得t=1,∴N(﹣3,0),M(﹣3,3),
∵DM=GN=2t=2,∴D(﹣1,3),
设直线AD的解析式为y=kx+b,
则,解得,∴y=3x+6.
(3)由(1)、(2)得,C(﹣,3),D(﹣1,3),∴CD=﹣1﹣(﹣)=,
∴S△ACD=××3=,
过点E作直线y=3的垂线,垂足为点F,
∵点E在直线y=3x+6上,且点E的横坐标为m,∴E(m,3m+6),
如图3,点E在线段AD上,则﹣2<m≤﹣1,
此时,EF=3﹣(3m+6)=﹣3m﹣3,
由S△ACE=S△ACD﹣S△ECD得,
S=﹣×(﹣3m﹣3)=m+;
如图4,点E在线段AD的延长线上,则m>﹣1,
此时,EF=3m+6﹣3=3m+3,
由S△ACE=S△ACD+S△ECD得,
S=+×(3m+3)=m+,
∴当m>﹣2时,S=m+;
如图5,点E在线段DA的延长线上,则m<﹣2,
此时,EF=3﹣(3m+6)=﹣3m﹣3,
由S△ACE=S△ECD﹣S△ACD得,
S=×(﹣3m﹣3)﹣=﹣m﹣,
综上所述,.
每日一题50参考答案
50.解:(1)由直线y=kx+b分别与x轴、y轴交于点A(0,8)、B(4,0)得,
,解得,∴y=﹣2x+8,
∵点M(2,m)在y=﹣2x+8上,∴m=﹣2×2+8=4.
(2)存在.如图1,连接BD,∵AD OB=AD DE+OD DE=S△ABD,
∴4AD=(AD+OD)DE=8DE,∴AD=2DE;
当CE=CD时,作CF⊥DE于点F,则DF=EF,
设直线CD的解析式为y=﹣x+n,
∵C(t,0),∴﹣t+n=0,解得n=t,∴y=﹣x+t,∴D(0,t),∴F(t,t),
∴DE=2DF=2t,∴8﹣t=2×2t,解得,t=;
当ED=CD时,如图2,
∵∠COD=90°,OC=OD=t,∴CD==t,∴8﹣t=2×t,
解得,t=,综上所述,t=或t=.
(3)如图3,过点M作MH⊥OB于点H,作NG⊥MH交HM的延长线于点G,
∵∠G=∠MHC=90°,∠CMN=90°,∴∠GNM=90°﹣∠GMN=∠HMC,
∵MN=CM,∴△MNG≌△CMH(AAS),
由(1)得,M(2,4),∴GN=HM=4,
∵2﹣4=﹣2,∴点N的横坐标为﹣2,∴点N在直线l:x=﹣2上运动;
作点A关于直线l的对称点A′,连接MA′交直线l于点N′,则A′(﹣4,8),
当点N接近点N′时,AN+MN的值最小,此时点C与点O重合,
∴MG=CH=2,∴N(﹣2,6),
∴AN+MN=+=2+2,
AN+MN的最小值为2+2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
