浙教版八年级上册数学每日一题51-55(第5章 一次函数)培优练习(含答案)
文档属性
| 名称 | 浙教版八年级上册数学每日一题51-55(第5章 一次函数)培优练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
每日一题51
班级 姓名 小组
51.如图,四边形OABC是一张放在平面直角坐标系中的正方形纸片,点O与坐标原点重合,点A在x轴上,点C在y轴上,OC=5,点E在边BC上,点N的坐标为(3,0),过点N且平行于y轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为OE.
(1)求点G的坐标,并求直线OG的解析式;
(2)若直线l:y=mx+n平行于直线OG,且与长方形ABMN有公共点,请直接写出n的取值范围.
(3)设点P为x轴上的点,是否存在这样的点P,使得以P,O,G为顶点的三角形为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
每日一题52
班级 姓名 小组
52.如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于A,B两点,点C(2,m)为直线y=x+2上一点,直线y=﹣x+b过点C.
(1)求m和b的值;
(2)直线y=﹣x+b与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动.设点P的运动时间为t秒.
①若点P在线段DA上,且△ACP的面积为10,求t的值;
②是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
每日一题53
班级 姓名 小组
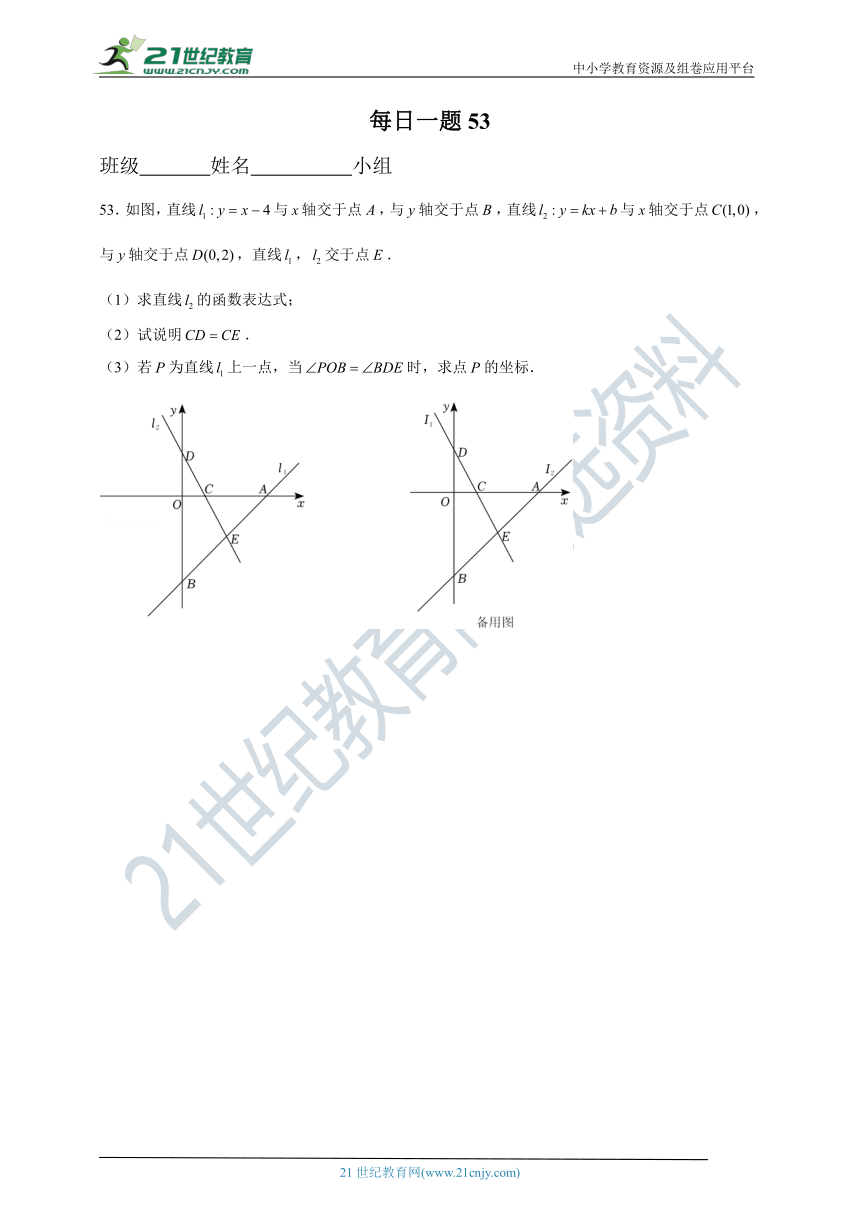
53.如图,直线与轴交于点,与轴交于点,直线与轴交于点,与轴交于点,直线,交于点.
(1)求直线的函数表达式;
(2)试说明.
(3)若为直线上一点,当时,求点的坐标.
每日一题54
班级 姓名 小组
54.(1)问题解决:如图1,在平面直角坐标系中,一次函数与轴交于点,与轴交于点,以为腰在第二象限作等腰直角,,点、、的坐标分别为 、 、 .
(2)综合运用:①如图2,在平面直角坐标系中,点坐标,点坐标,过点作轴垂线,点是上一动点,点是在一次函数图象上一动点,若是以点为直角顶点的等腰直角三角形,请求出点的坐标.
②如图2,在(2)的条件中,若为轴上一动点,连接,把绕点逆时针旋转至线段,的最小值是 .
每日一题55
班级 姓名 小组
55.请你用学习“一次函数”中积累的经验和方法研究函数的图象和性质,并解决问题.
(1)①当时,;
②当时, ;
③当时, ;
显然,②和③均为某个一次函数的一部分.
(2)在平面直角坐标系中,作出函数的图象.
(3)根据函数图象写出函数的一条性质: .
(4)一次函数为常数,的图象过点,若无解,结合函数的图象,直接写出的取值范围.
每日一题51参考答案
51.解:(1)如图1,由题意得,C(0,5),N(3,0),∴ON=3,
由折叠得,OG=OC=5,∵∠ONG=90°,∴NG===4,∴G(3,4),
设直线OG的解析式为y=kx,则3k=4,解得,k=,∴直线OG的解析式为y=x,
(2)∵直线l:y=mx+n平行于直线OG,∴m=,∴y=x+n;
由题意得,A(5,0),M(3,5),
如图2,当直线l经过点A时,n的值最小,则×5+n=0,解得,n=;
如图3,当直线l经过点M时,n的值最大,则×3+n=5,解得,n=1,
∴n的取值范围是≤n≤1.
(3)存在,设P(x,0),当x<0时,如图4,由OP=OG=5,得x=﹣5,
∴P(﹣5,0);当x>0时,如图5,PO=PG=x,则PN=x﹣3,
∵∠PNG=90°,∴PG2=PN2+GN2,∴x2=(x﹣3)2+42,解得,x=,∴P(,0);
如图6,OP=OG=5,∴P(5,0);如图7,PG=OG,∵GN⊥PO,∴PN=ON=3,
∴OP=6,∴P(6,0).综上所述,点P的坐标为(﹣5,0)或(,0)或(5,0)或(6,0).
每日一题52参考答案
【解答】解:(1)把点C(2,m)代入直线y=x+2中得:m=2+2=4,∴点C(2,4),
∵直线y=﹣x+b过点C,4=﹣+b,b=5;
(2)①由题意得:PD=t,y=x+2中,当y=0时,x+2=0,x=﹣2,
∴A(﹣2,0),y=﹣x+5中,当y=0时,﹣x+5=0,
x=10,∴D(10,0),∴AD=10+2=12,即0≤t≤12,
∵△ACP的面积为10,∴ 4=10,t=7,则t的值7秒;
②存在,分三种情况:
i)当AC=CP时,如图1,过C作CE⊥AD于E,∴PE=AE=4,∴PD=12﹣8=4,即t=4;
ii)当AC=AP时,如图2,AC=AP1=AP2==4,∴DP1=t=12﹣4,
DP2=t=12+4;
iii)当AP=PC时,如图3,∵OA=OB=2∴∠BAO=45°
∴∠CAP=∠ACP=45°∴∠APC=90°∴AP=PC=4∴PD=12﹣4=8,即t=8;
综上,当t=4秒或(12﹣4)秒或(12+4)秒或8秒时,△ACP为等腰三角形.
每日一题53参考答案
53.解:(1)将.代入得,,解得,
直线的函数解析式为;
(2)当时,,,
过点作轴于,
,
,,,;
(3),点在上有两个位置,
当点在点上方时,如图,
,
直线的函数解析式为,,,
当时,,,,
当点在点的下方时,设点关于轴的对称点为,连接交为点,
,,
则直线的函数解析式为,直线与的交点为,
综上所述:,或.
每日一题54 参考答案
54.解:(1)对于一次函数,令,,,
令,则,,,,,
,,过点作轴于,
,,
,,,
是等腰直角三角形,,
在和中,
,,,,
,;
故答案为:,,;
(2)①如图,过点作轴于,延长交于,
点坐标,点坐标,,
点在直线上,设点,
,,,
轴,,,
同(1)的方法得,,,,
,,或,或,,
(3)设,过点作轴交轴于,
根据旋转的性质可得,
,,,,
故可以看作点到和两点距离之和,在上,如图,
是上的动点,,,
,关于的对称点为,,
当、、三点共线时,取得最小值为,
即的最小值是.故答案为:.
每日一题55参考答案
【解答】解:(1)②时,,
时,,
③时,,
时,,
故答案为:,.
(2)如图,
(3)由图象可得,函数图象关于轴对称,
故答案为:函数图象关于轴对称.
(4)当时,如图,当直线与时,方程无解,此时,
当时,满足题意.
如图,当直线经过,时,
将,代入得,解得,
时满足题意,综上所述,若无解,且.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题51
班级 姓名 小组
51.如图,四边形OABC是一张放在平面直角坐标系中的正方形纸片,点O与坐标原点重合,点A在x轴上,点C在y轴上,OC=5,点E在边BC上,点N的坐标为(3,0),过点N且平行于y轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落在MN上,并与MN上的点G重合,折痕为OE.
(1)求点G的坐标,并求直线OG的解析式;
(2)若直线l:y=mx+n平行于直线OG,且与长方形ABMN有公共点,请直接写出n的取值范围.
(3)设点P为x轴上的点,是否存在这样的点P,使得以P,O,G为顶点的三角形为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
每日一题52
班级 姓名 小组
52.如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于A,B两点,点C(2,m)为直线y=x+2上一点,直线y=﹣x+b过点C.
(1)求m和b的值;
(2)直线y=﹣x+b与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动.设点P的运动时间为t秒.
①若点P在线段DA上,且△ACP的面积为10,求t的值;
②是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
每日一题53
班级 姓名 小组
53.如图,直线与轴交于点,与轴交于点,直线与轴交于点,与轴交于点,直线,交于点.
(1)求直线的函数表达式;
(2)试说明.
(3)若为直线上一点,当时,求点的坐标.
每日一题54
班级 姓名 小组
54.(1)问题解决:如图1,在平面直角坐标系中,一次函数与轴交于点,与轴交于点,以为腰在第二象限作等腰直角,,点、、的坐标分别为 、 、 .
(2)综合运用:①如图2,在平面直角坐标系中,点坐标,点坐标,过点作轴垂线,点是上一动点,点是在一次函数图象上一动点,若是以点为直角顶点的等腰直角三角形,请求出点的坐标.
②如图2,在(2)的条件中,若为轴上一动点,连接,把绕点逆时针旋转至线段,的最小值是 .
每日一题55
班级 姓名 小组
55.请你用学习“一次函数”中积累的经验和方法研究函数的图象和性质,并解决问题.
(1)①当时,;
②当时, ;
③当时, ;
显然,②和③均为某个一次函数的一部分.
(2)在平面直角坐标系中,作出函数的图象.
(3)根据函数图象写出函数的一条性质: .
(4)一次函数为常数,的图象过点,若无解,结合函数的图象,直接写出的取值范围.
每日一题51参考答案
51.解:(1)如图1,由题意得,C(0,5),N(3,0),∴ON=3,
由折叠得,OG=OC=5,∵∠ONG=90°,∴NG===4,∴G(3,4),
设直线OG的解析式为y=kx,则3k=4,解得,k=,∴直线OG的解析式为y=x,
(2)∵直线l:y=mx+n平行于直线OG,∴m=,∴y=x+n;
由题意得,A(5,0),M(3,5),
如图2,当直线l经过点A时,n的值最小,则×5+n=0,解得,n=;
如图3,当直线l经过点M时,n的值最大,则×3+n=5,解得,n=1,
∴n的取值范围是≤n≤1.
(3)存在,设P(x,0),当x<0时,如图4,由OP=OG=5,得x=﹣5,
∴P(﹣5,0);当x>0时,如图5,PO=PG=x,则PN=x﹣3,
∵∠PNG=90°,∴PG2=PN2+GN2,∴x2=(x﹣3)2+42,解得,x=,∴P(,0);
如图6,OP=OG=5,∴P(5,0);如图7,PG=OG,∵GN⊥PO,∴PN=ON=3,
∴OP=6,∴P(6,0).综上所述,点P的坐标为(﹣5,0)或(,0)或(5,0)或(6,0).
每日一题52参考答案
【解答】解:(1)把点C(2,m)代入直线y=x+2中得:m=2+2=4,∴点C(2,4),
∵直线y=﹣x+b过点C,4=﹣+b,b=5;
(2)①由题意得:PD=t,y=x+2中,当y=0时,x+2=0,x=﹣2,
∴A(﹣2,0),y=﹣x+5中,当y=0时,﹣x+5=0,
x=10,∴D(10,0),∴AD=10+2=12,即0≤t≤12,
∵△ACP的面积为10,∴ 4=10,t=7,则t的值7秒;
②存在,分三种情况:
i)当AC=CP时,如图1,过C作CE⊥AD于E,∴PE=AE=4,∴PD=12﹣8=4,即t=4;
ii)当AC=AP时,如图2,AC=AP1=AP2==4,∴DP1=t=12﹣4,
DP2=t=12+4;
iii)当AP=PC时,如图3,∵OA=OB=2∴∠BAO=45°
∴∠CAP=∠ACP=45°∴∠APC=90°∴AP=PC=4∴PD=12﹣4=8,即t=8;
综上,当t=4秒或(12﹣4)秒或(12+4)秒或8秒时,△ACP为等腰三角形.
每日一题53参考答案
53.解:(1)将.代入得,,解得,
直线的函数解析式为;
(2)当时,,,
过点作轴于,
,
,,,;
(3),点在上有两个位置,
当点在点上方时,如图,
,
直线的函数解析式为,,,
当时,,,,
当点在点的下方时,设点关于轴的对称点为,连接交为点,
,,
则直线的函数解析式为,直线与的交点为,
综上所述:,或.
每日一题54 参考答案
54.解:(1)对于一次函数,令,,,
令,则,,,,,
,,过点作轴于,
,,
,,,
是等腰直角三角形,,
在和中,
,,,,
,;
故答案为:,,;
(2)①如图,过点作轴于,延长交于,
点坐标,点坐标,,
点在直线上,设点,
,,,
轴,,,
同(1)的方法得,,,,
,,或,或,,
(3)设,过点作轴交轴于,
根据旋转的性质可得,
,,,,
故可以看作点到和两点距离之和,在上,如图,
是上的动点,,,
,关于的对称点为,,
当、、三点共线时,取得最小值为,
即的最小值是.故答案为:.
每日一题55参考答案
【解答】解:(1)②时,,
时,,
③时,,
时,,
故答案为:,.
(2)如图,
(3)由图象可得,函数图象关于轴对称,
故答案为:函数图象关于轴对称.
(4)当时,如图,当直线与时,方程无解,此时,
当时,满足题意.
如图,当直线经过,时,
将,代入得,解得,
时满足题意,综上所述,若无解,且.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
