浙教版八年级下册数学每日一题61-65(第四章 平行四边形)培优练习(含解析)
文档属性
| 名称 | 浙教版八年级下册数学每日一题61-65(第四章 平行四边形)培优练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 14:11:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
每日一题61
班级 姓名 小组
61.如图,在 ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.
(1)求证:∠OBE=∠ADO;
(2)若F,G分别是OD,AB的中点,且BC=10,
①求证:△EFG是等腰三角形;
②当EF⊥EG时,求 ABCD的面积.
每日一题62
班级 姓名 小组
62.已知,平行四边形ABCD中,一动点P在AD边上,以每秒1cm的速度从点A向点D运动.
(1)如图①,运动过程中,若CP平分∠BCD,且满足CD=CP,求∠ABC的度数.
(2)如图②,在(1)问的条件下,连接BP并延长,与CD的延长线交于点F,连接AF,若AB=8cm,求△APF的面积.
(3)如图③,另一动点Q在BC边上,以每秒4cm的速度从点C出发,在BC间往返运动,两个点同时出发,当点P到达点D时停止运动(同时Q点也停止),若AD=12cm,则t为何值时,以P,D,Q,B四点组成的四边形是平行四边形.
每日一题63
班级 姓名 小组
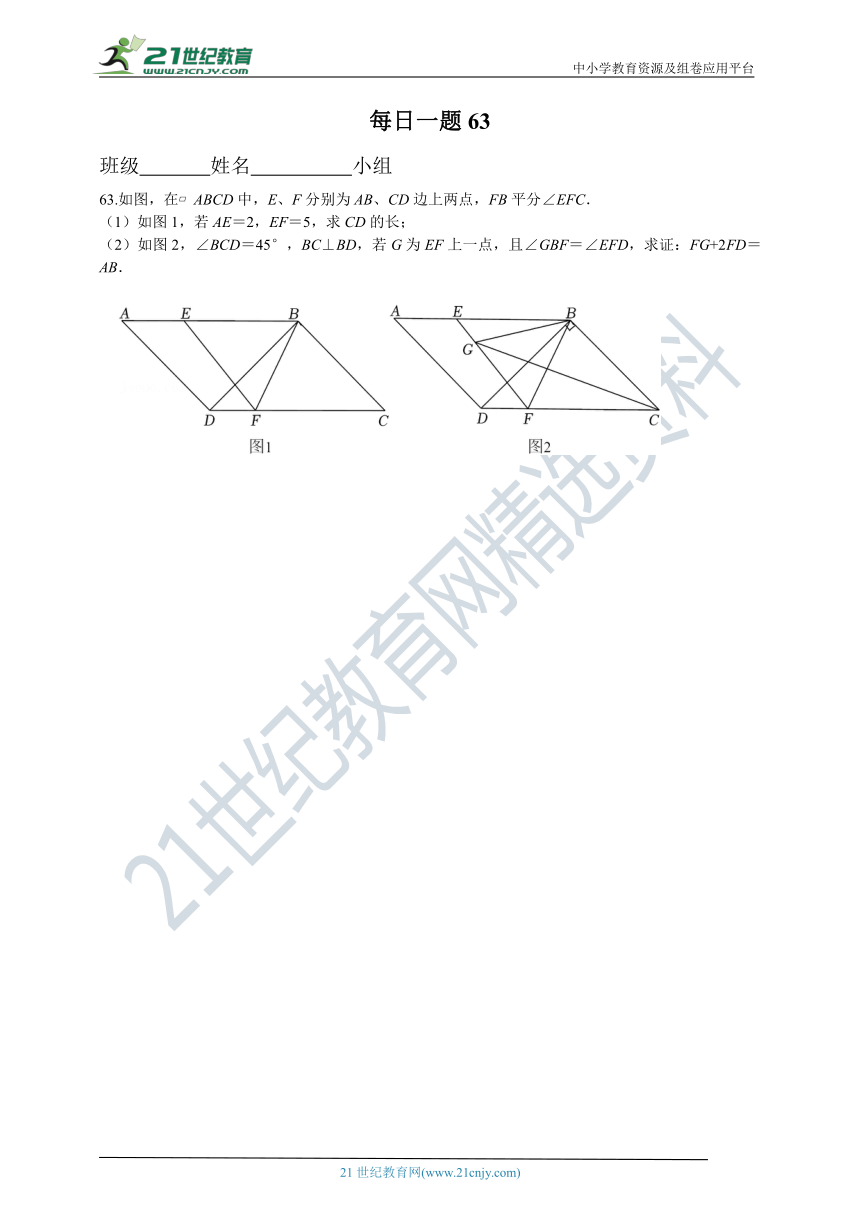
63.如图,在 ABCD中,E、F分别为AB、CD边上两点,FB平分∠EFC.
(1)如图1,若AE=2,EF=5,求CD的长;
(2)如图2,∠BCD=45°,BC⊥BD,若G为EF上一点,且∠GBF=∠EFD,求证:FG+2FD=AB.
每日一题64
班级 姓名 小组
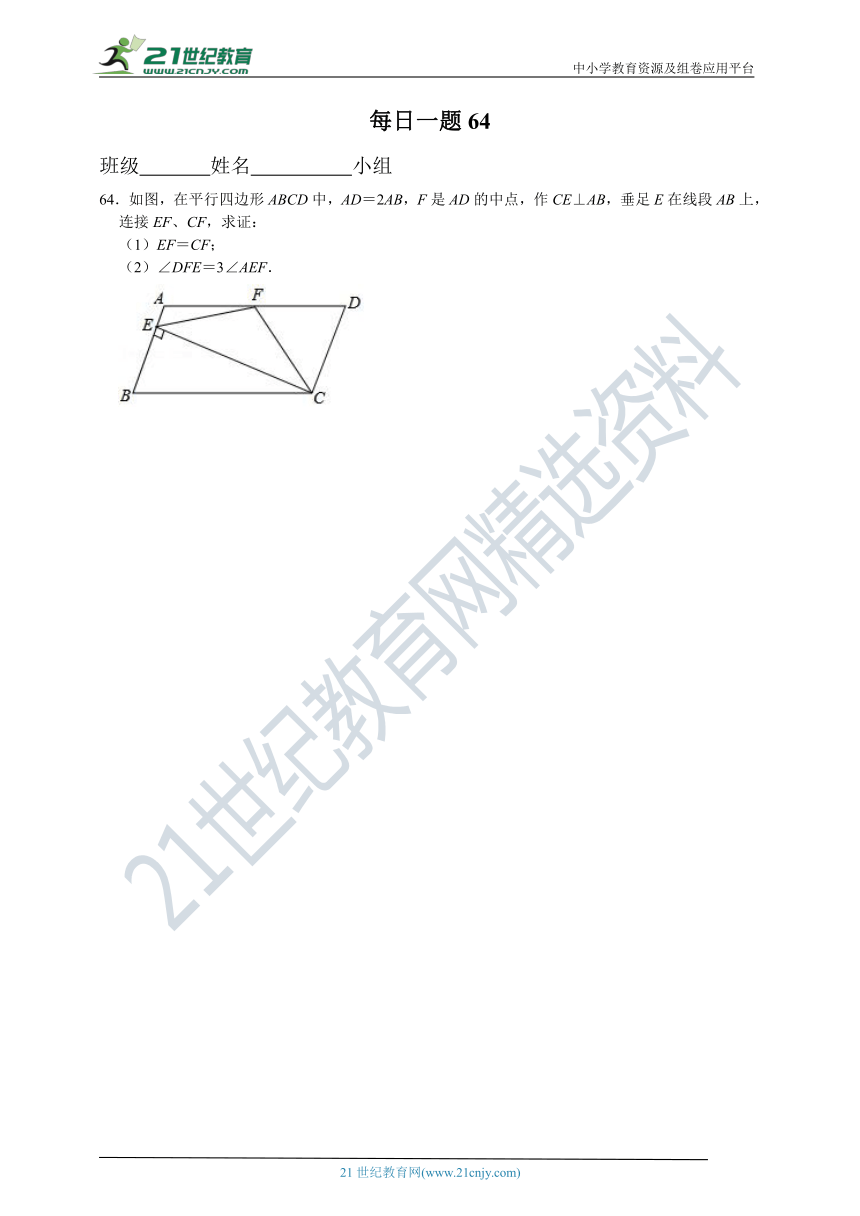
64.如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,求证:
(1)EF=CF;
(2)∠DFE=3∠AEF.
每日一题65
班级 姓名 小组
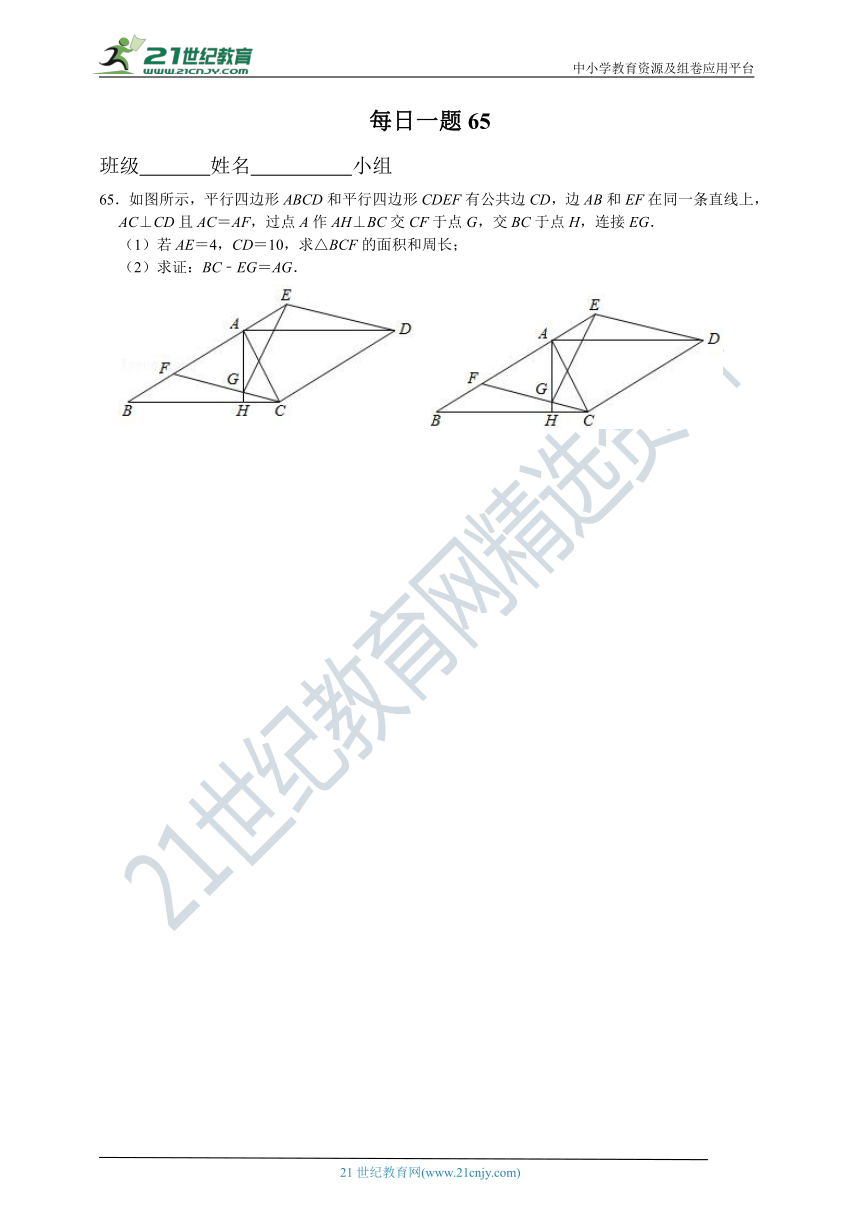
65.如图所示,平行四边形ABCD和平行四边形CDEF有公共边CD,边AB和EF在同一条直线上,AC⊥CD且AC=AF,过点A作AH⊥BC交CF于点G,交BC于点H,连接EG.
(1)若AE=4,CD=10,求△BCF的面积和周长;
(2)求证:BC﹣EG=AG.
每日一题61参考答案
61.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,DO=BO=BD,∴∠ADB=∠DBC,
∵BD=2AD,∴AD=DO,∴BC=BO,
∵E是CO中点,∴∠OBE=∠OBC,∴∠OBE=∠ADO;
(2)①证明:∵BC=BO,∴△BOC是等腰三角形,
∵E是CO中点,∴EB⊥CO,∴∠BEA=90°,
∵G为AB中点,∴EG=AB,
∵四边形ABCD是平行四边形,∴AB=CD,
∵E、F分别是OC、OD的中点,∴EF=CD ∴EG=EF,
∴△EFG是等腰三角形;
②解:由①得EF∥AB,∵EF⊥EG,∴EG⊥AB,
∵G是AB的中点,∴AE=BE,
设CE=x,则AO=CO=2CE=2x,∴BE=AE=3x,
在Rt△BEC中,BC=10,∴EC2+BE2=BC2,
即x2+(3x)2=102,解得x=,
∴AC=,BE=,∴S ABCD=2S△ABC=.
每日一题62 参考答案
62.解:(1)如图①中,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DPC=∠PCB,
∵PC平分∠BCD,
∴∠PCD=∠PCB,
∴∠DPC=∠DCP,
∴DP=DC,
∵CD=CP,
∴PC=CD=PD,
∴△PDC是等边三角形,
∴∠D=∠B=60°.
(2)如图②中,
∵四边形ABCD是平行四边形,
∴AB∥CD,BC∥AD,
∴S△PBC=S△FAB=S平行四边形ABCD,
∴S△ABP+S△PCD=S平行四边形ABCD,
∴S△APF+S△ABP=S△ABP+S△PCD,
∴S△APF=S△PCD= 82=16.
(3)如图③中,
∵PD∥BC,
∴当PD=BQ时,四边形PDQB是平行四边形,
∴12﹣t=12﹣4t或12﹣t=4t﹣12或12﹣t=36﹣4t或12﹣t=4t﹣36,
解得t=4.8或8或9.6,
∴t为4.8s或8s或9.6 s时,以P,D,Q,B四点组成的四边形是平行四边形.
每日一题63 参考答案
63.(1)解:在 ABCD中,AB∥CD,AB=CD,
∴∠ABF=∠BFC,
∵FB平分∠EFC,
∴∠EFB=∠BFC,
∴∠ABF=∠EFB,
∵AE=2,EF=5,
∴BE=EF=5,
∴CD=AB=AE+EF=2+5=7;
(2)证明:在FC上截取FH=FG,连接BH,
在△BGF和△BHF中,
,
∴△BGF≌△BHF(SAS),
∴∠BGF=∠BHF,
∵∠GBF=∠EFD,
∵∠EFD+∠EFB+∠BFH=180°,∠EFB+∠BGF+∠GBF=180°,
∴∠BFH=∠BGF,
∴∠BFH=∠BHF,
∴∠BFD=∠BHC,
∵∠BCD=45°,BC⊥BD,
∴∠BDF=45°=∠BCH,
∴BD=BC,
在△BDF和△BCH中,
,
∴△BDF≌△BCH(AAS)
∴DF=CH,
∴AB=CD=DF+FH+CH=FG+2FD,
即FG+2FD=AB.
每日一题64 参考答案
64.解:(1)证明:延长CF交BA的延长线于G,延长EF交CD的延长线于R.如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵F是AD的中点,
∴CF=GF,EF=ER,
∴四边形EGRC是平行四边形,
∵CE⊥AB,
∴∠CEG=90°,
∴四边形EGRC是矩形,
∴CG=ER,
∴EF=CG=CF=GF,
即EF=CF;
(2)∵EF=GF,
∴∠G=∠FEG,
∵AD∥BC,CF=GF,
∴AG=AB,
∴AF=AG,
∴∠G=∠AFG=∠DFC,
∵∠CFE=∠G+∠AEF,
∴∠DFE=∠CFE+∠DFC=3∠AEF.
每日一题65 参考答案
65.(1)解:∵四边形ABCD,四边形CDEF是平行四边形,
∴AB=CD=10,CD=EF,AB∥CD,
∴AB=EF=10,
∴AE=BF=4,
∴AF=AC=6,
∵AB∥CD,AC⊥CD
∴AB⊥AC,
∴CF===6,
BC===2,
∴△BCF的面积=BF AC=×4×6=12,
△BCF的周长=BF+BC+CF=4+6+2;
(2)证明:如图,在AD上取一点M,使得AM=AG,连接CM.
∵四边形ABCD,四边形EFCD都是平行四边形,
∴AB=CD=EF,AD=BC,AD∥BC,AB∥CD,
∵AH⊥BC,
∴AH⊥AD,
∵AC⊥AB,
∴∠BAC=∠GAM=90°,
∴∠FAG=∠CAM,
∵AF=AC,AG=AM,
∴△FAG≌△CAM(SAS),
∴∠ACM=∠AFG=45°,FG=CM.
∵∠ACD=∠BAC=90°,
∴∠MCD=45°=∠EFG,
∵EF=CD,FG=CM,
∴△EFG≌△DCM(SAS),
∴EG=DM,
∴AG+EG=AM+DM=AD=BC.
即BC﹣EG=AG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题61
班级 姓名 小组
61.如图,在 ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.
(1)求证:∠OBE=∠ADO;
(2)若F,G分别是OD,AB的中点,且BC=10,
①求证:△EFG是等腰三角形;
②当EF⊥EG时,求 ABCD的面积.
每日一题62
班级 姓名 小组
62.已知,平行四边形ABCD中,一动点P在AD边上,以每秒1cm的速度从点A向点D运动.
(1)如图①,运动过程中,若CP平分∠BCD,且满足CD=CP,求∠ABC的度数.
(2)如图②,在(1)问的条件下,连接BP并延长,与CD的延长线交于点F,连接AF,若AB=8cm,求△APF的面积.
(3)如图③,另一动点Q在BC边上,以每秒4cm的速度从点C出发,在BC间往返运动,两个点同时出发,当点P到达点D时停止运动(同时Q点也停止),若AD=12cm,则t为何值时,以P,D,Q,B四点组成的四边形是平行四边形.
每日一题63
班级 姓名 小组
63.如图,在 ABCD中,E、F分别为AB、CD边上两点,FB平分∠EFC.
(1)如图1,若AE=2,EF=5,求CD的长;
(2)如图2,∠BCD=45°,BC⊥BD,若G为EF上一点,且∠GBF=∠EFD,求证:FG+2FD=AB.
每日一题64
班级 姓名 小组
64.如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,求证:
(1)EF=CF;
(2)∠DFE=3∠AEF.
每日一题65
班级 姓名 小组
65.如图所示,平行四边形ABCD和平行四边形CDEF有公共边CD,边AB和EF在同一条直线上,AC⊥CD且AC=AF,过点A作AH⊥BC交CF于点G,交BC于点H,连接EG.
(1)若AE=4,CD=10,求△BCF的面积和周长;
(2)求证:BC﹣EG=AG.
每日一题61参考答案
61.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,DO=BO=BD,∴∠ADB=∠DBC,
∵BD=2AD,∴AD=DO,∴BC=BO,
∵E是CO中点,∴∠OBE=∠OBC,∴∠OBE=∠ADO;
(2)①证明:∵BC=BO,∴△BOC是等腰三角形,
∵E是CO中点,∴EB⊥CO,∴∠BEA=90°,
∵G为AB中点,∴EG=AB,
∵四边形ABCD是平行四边形,∴AB=CD,
∵E、F分别是OC、OD的中点,∴EF=CD ∴EG=EF,
∴△EFG是等腰三角形;
②解:由①得EF∥AB,∵EF⊥EG,∴EG⊥AB,
∵G是AB的中点,∴AE=BE,
设CE=x,则AO=CO=2CE=2x,∴BE=AE=3x,
在Rt△BEC中,BC=10,∴EC2+BE2=BC2,
即x2+(3x)2=102,解得x=,
∴AC=,BE=,∴S ABCD=2S△ABC=.
每日一题62 参考答案
62.解:(1)如图①中,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DPC=∠PCB,
∵PC平分∠BCD,
∴∠PCD=∠PCB,
∴∠DPC=∠DCP,
∴DP=DC,
∵CD=CP,
∴PC=CD=PD,
∴△PDC是等边三角形,
∴∠D=∠B=60°.
(2)如图②中,
∵四边形ABCD是平行四边形,
∴AB∥CD,BC∥AD,
∴S△PBC=S△FAB=S平行四边形ABCD,
∴S△ABP+S△PCD=S平行四边形ABCD,
∴S△APF+S△ABP=S△ABP+S△PCD,
∴S△APF=S△PCD= 82=16.
(3)如图③中,
∵PD∥BC,
∴当PD=BQ时,四边形PDQB是平行四边形,
∴12﹣t=12﹣4t或12﹣t=4t﹣12或12﹣t=36﹣4t或12﹣t=4t﹣36,
解得t=4.8或8或9.6,
∴t为4.8s或8s或9.6 s时,以P,D,Q,B四点组成的四边形是平行四边形.
每日一题63 参考答案
63.(1)解:在 ABCD中,AB∥CD,AB=CD,
∴∠ABF=∠BFC,
∵FB平分∠EFC,
∴∠EFB=∠BFC,
∴∠ABF=∠EFB,
∵AE=2,EF=5,
∴BE=EF=5,
∴CD=AB=AE+EF=2+5=7;
(2)证明:在FC上截取FH=FG,连接BH,
在△BGF和△BHF中,
,
∴△BGF≌△BHF(SAS),
∴∠BGF=∠BHF,
∵∠GBF=∠EFD,
∵∠EFD+∠EFB+∠BFH=180°,∠EFB+∠BGF+∠GBF=180°,
∴∠BFH=∠BGF,
∴∠BFH=∠BHF,
∴∠BFD=∠BHC,
∵∠BCD=45°,BC⊥BD,
∴∠BDF=45°=∠BCH,
∴BD=BC,
在△BDF和△BCH中,
,
∴△BDF≌△BCH(AAS)
∴DF=CH,
∴AB=CD=DF+FH+CH=FG+2FD,
即FG+2FD=AB.
每日一题64 参考答案
64.解:(1)证明:延长CF交BA的延长线于G,延长EF交CD的延长线于R.如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∵F是AD的中点,
∴CF=GF,EF=ER,
∴四边形EGRC是平行四边形,
∵CE⊥AB,
∴∠CEG=90°,
∴四边形EGRC是矩形,
∴CG=ER,
∴EF=CG=CF=GF,
即EF=CF;
(2)∵EF=GF,
∴∠G=∠FEG,
∵AD∥BC,CF=GF,
∴AG=AB,
∴AF=AG,
∴∠G=∠AFG=∠DFC,
∵∠CFE=∠G+∠AEF,
∴∠DFE=∠CFE+∠DFC=3∠AEF.
每日一题65 参考答案
65.(1)解:∵四边形ABCD,四边形CDEF是平行四边形,
∴AB=CD=10,CD=EF,AB∥CD,
∴AB=EF=10,
∴AE=BF=4,
∴AF=AC=6,
∵AB∥CD,AC⊥CD
∴AB⊥AC,
∴CF===6,
BC===2,
∴△BCF的面积=BF AC=×4×6=12,
△BCF的周长=BF+BC+CF=4+6+2;
(2)证明:如图,在AD上取一点M,使得AM=AG,连接CM.
∵四边形ABCD,四边形EFCD都是平行四边形,
∴AB=CD=EF,AD=BC,AD∥BC,AB∥CD,
∵AH⊥BC,
∴AH⊥AD,
∵AC⊥AB,
∴∠BAC=∠GAM=90°,
∴∠FAG=∠CAM,
∵AF=AC,AG=AM,
∴△FAG≌△CAM(SAS),
∴∠ACM=∠AFG=45°,FG=CM.
∵∠ACD=∠BAC=90°,
∴∠MCD=45°=∠EFG,
∵EF=CD,FG=CM,
∴△EFG≌△DCM(SAS),
∴EG=DM,
∴AG+EG=AM+DM=AD=BC.
即BC﹣EG=AG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
