浙教版八年级下册数学每日一题66-70(第四章 平行四边形)培优练习(含解析)
文档属性
| 名称 | 浙教版八年级下册数学每日一题66-70(第四章 平行四边形)培优练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 14:34:58 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
每日一题66
班级 姓名 小组
66.如图,在四边形ABCD中,∠A=∠B=∠BCD=90°,AB=DC=4,AD=BC=8.延长BC到E,使CE=3,连接DE,由直角三角形的性质可知DE=5.动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒.(t>0)
(1)当t=3时,BP= ;
(2)当t= 时,点P运动到∠B的角平分线上;
(3)请用含t的代数式表示△ABP的面积S;
(4)当0<t<6时,直接写出点P到四边形ABED相邻两边距离相等时t的值.
每日一题67
班级 姓名 小组
67.如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连接PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.
每日一题68
班级 姓名 小组
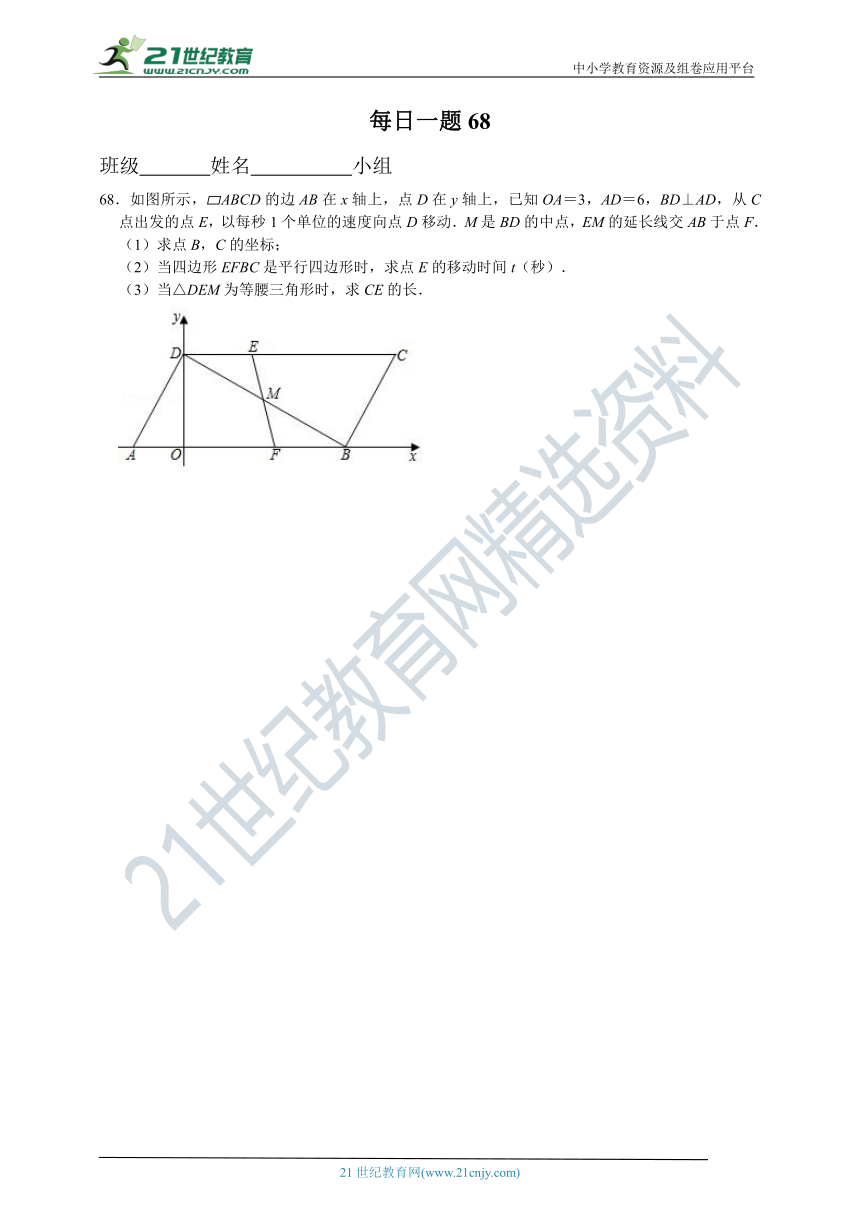
68.如图所示, ABCD的边AB在x轴上,点D在y轴上,已知OA=3,AD=6,BD⊥AD,从C点出发的点E,以每秒1个单位的速度向点D移动.M是BD的中点,EM的延长线交AB于点F.
(1)求点B,C的坐标;
(2)当四边形EFBC是平行四边形时,求点E的移动时间t(秒).
(3)当△DEM为等腰三角形时,求CE的长.
每日一题69
班级 姓名 小组
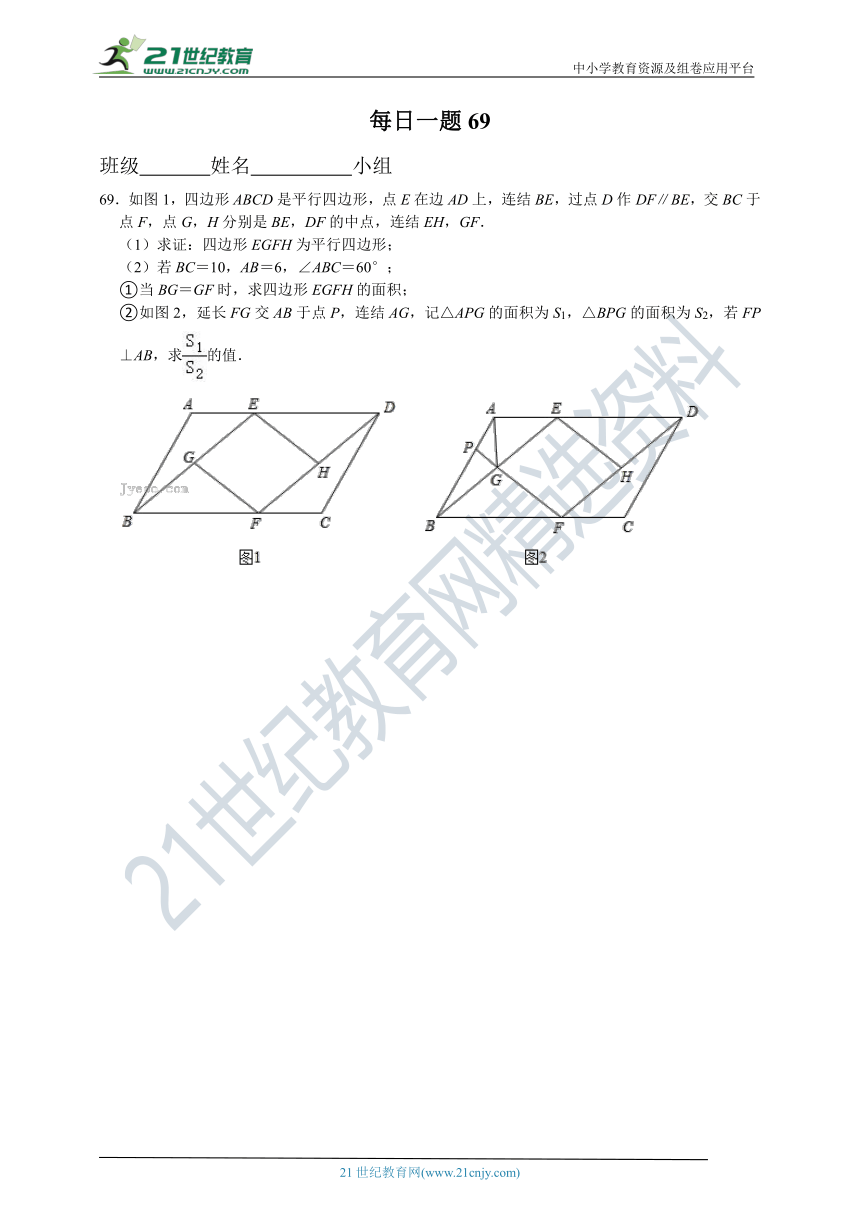
69.如图1,四边形ABCD是平行四边形,点E在边AD上,连结BE,过点D作DF∥BE,交BC于点F,点G,H分别是BE,DF的中点,连结EH,GF.
(1)求证:四边形EGFH为平行四边形;
(2)若BC=10,AB=6,∠ABC=60°;
①当BG=GF时,求四边形EGFH的面积;
②如图2,延长FG交AB于点P,连结AG,记△APG的面积为S1,△BPG的面积为S2,若FP⊥AB,求的值.
每日一题70
班级 姓名 小组
70.定义:我们把对角线长度相等的四边形叫做等线四边形.
(1)尝试:如图1,在3×3的正方形网格图形中,已知点A、点B是两个格点,请你作出一个等线四边形,要求A、B是其中两个顶点,且另外两个顶点也是格点;
(2)推理:如图2,已知△AOD与△BOC均为等腰直角三角形,∠AOD=∠BOC=90°,连结AB,CD,求证:四边形ABCD是等线四边形;
(3)拓展:如图3,已知四边形ABCD是等线四边形,对角线AC,BD交于点O,若∠AOD=60°,AB=,BC=,AD=2.求CD的长.
每日一题66参考答案
66.解:(1)BP=2t=2×3=6,故答案为:6;
(2)作∠B的角平分线交AD于F,
∴∠ABF=∠FBC,
∵∠A=∠ABC=∠BCD=90°,∴四边形ABCD是矩形,
∵AD∥BC,∴∠AFB=∠FBC,
∴∠ABF=∠AFB,∴AF=AB=4,
∴DF=AD﹣AF=8﹣4=4,∴BC+CD+DF=8+4+4=16,
∴2t=16,解得t=8.
∴当t=8时,点P运动到∠ABC的角平分线上;故答案为:8;
(3)根据题意分3种情况讨论:
①当点P在BC上运动时,S△ABP=×BP×AB=×2t×4=4t;(0<t<4);
②当点P在CD上运动时,S△ABP=×AB×BC=×4×8=16;(4≤t≤6);
③当点P在AD上运动时,S△ABP=×AB×AP=×4×(20﹣2t)=﹣4t+40;(6<t≤10);
(4)当0<t<6时,点P在BC、CD边上运动,
根据题意分情况讨论:
①当点P在BC上,点P到四边形ABED相邻两边距离相等,
∴点P到AD边的距离为4,∴点P到AB边的距离也为4,即BP=4,
∴2t=4,解得t=2s;
②当点P在BC上,点P到AD边的距离为4,∴点P到DE边的距离也为4,
∴PE=DE=5,∴PC=PE﹣CE=2,∴8﹣2t=2,解得t=3s;
③当点P在CD上,如图,过点P作PH⊥DE于点H,
点P到DE、BE边的距离相等,即PC=PH,
∵PC=2t﹣8,∵S△DCE=S△DPE+S△PCE,
∴3×4=5×PH+3×PC,
∴12=8PH,∴12=8(2t﹣8),解得t=.
综上所述:t=2或t=3或t=时,点P到四边形ABED相邻两边距离相等.
每日一题67 参考答案
67.解:(1)作AM⊥BC于M,设AC交PE于N.如图所示:
∵∠BAC=90°,∠B=45°,∴∠C=45°=∠B,
∴AB=AC,∴BM=CM,∴AM=BC=5,
∵AD∥BC,∴∠PAN=∠C=45°,
∵PE⊥BC,∴PE=AM=5,PE⊥AD,
∴△APN和△CEN是等腰直角三角形,
∴PN=AP=t,CE=NE=5﹣t,
∵CE=CQ﹣QE=2t﹣2,∴5﹣t=2t﹣2,
解得:t=,所以BQ=BC﹣CQ=10﹣2×=;
(2)存在,t=4或12;理由如下:
若以A,B,E,P为顶点的四边形为平行四边形,则AP=BE,
∴t=10﹣2t+2或t=2t﹣2﹣10
解得:t=4或12
∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4或12.
每日一题68 参考答案
68.解:(1)∵OA=3,AD=6,
∴OD=3,
∴∠DAB=60°,
∵BD⊥AD,
∴△ADB是含30°角的直角三角形,
∴AB=2AD=12,
∵四边形ABCD是平行四边形,
∴AB=DC=12,
∴B坐标为(9,0),C坐标为(12,3);
(2)∵M是BD的中点,四边形EFBC是平行四边形,
∴EF∥BC时,点E是CD的中点,
∴CE=6,
∴t=6;
(3)当△DEM为等腰三角形时,①当MD=ME=BD=3时,∠BDC=30°,
∴DE=9,
∴CE=CD﹣DE=12﹣9=3,
②当DM=DE=BD=3时,
∴DE=3,
∴CE=CD﹣DE=12﹣3,
③当ED=EM时,DM=BD=3,
∵∠BDC=30°,
∴DE=3,
∴CE=CD﹣DE=12﹣3=9,
综上所述,当△DEM为等腰三角形时,CE的长为3或9或12﹣3.
每日一题69 参考答案
69.解:(1)如图1,
∵在平行四边形ABCD中,AD∥BC,DF∥BE,
∴四边形BFDE是平行四边形,∴BE=DF,
∵G、H分别是BE、DF的中点,∴EG=FH,
∵EG∥FH,∴四边形EGFH为平行四边形;
(2)①连接EF,
∵BG=GF、BG=EG,∴EG=FG=BG,∴∠1=∠2,∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴∠2+∠4=90°,即∠BFE=90°,
由(1)知,四边形EGFH为平行四边形,
∴S四边形EGFH=2S△EGF=S△BEF,
过点A作AM⊥BC,则EF∥AM,
∵AB=6,∠ABC=60°,
∴AM=3,BM=3,
∵AM∥EF,AE∥MF,∠AMF=90°,
∴四边形AMFE为矩形,
设DE=a,则BF=a,MF=BF﹣BM=a﹣3,AE=AD﹣AE=10﹣a,
∵a﹣3=10﹣a,
∴a=,
∴S四边形EGFH=S△BEF===;
②延长FG交DA的延长线于点N,
∵GE=GB,∠NEG=∠FBG,∠NGE=∠FGB,
∴△EGN≌△BGF(SAS),
∴NE=BF,
假设BP=a,则BF=DE=2a,AE=10﹣2a,AN=4a﹣10,AP=2a﹣5,
由AP+BP=6得a=,
∵△APG与△BPG同高,∴===.
每日一题70 参考答案
【70解:(1)如图1所示,矩形APBQ即为所求.
(2)证明:
如图2,连结AC,BD.
∵△AOD与△BOC均为等腰直角三角形,
∴OA=OD,OC=OB,∠AOD=∠BOC,
∴∠AOC=∠BOD,
∴△AOC≌△DOB(SAS),
∴BD=AC,
∴四边形ABCD是等线四边形.
(3)解:如图3,分别以AD、BC为底作等腰△ADE、等腰△BCE,顶点均为点E.
于是有,EA=ED,EC=EB,
∵AC=BD,
∴△AEC≌△DEB(SSS),
∴∠BDE=∠CAE,
∴∠AED=∠AOD=60°,
∴△AED是等边三角形.
同理,△BCE也是等边三角形.
∴EA=ED=AD=2,.
∵,
∴AE2+BE2=AB2,
∴∠AEB=90°,
∴∠DEC=150°.
过点C作CF⊥DE于交DE延长线于点F,则∠CEF=30°.
∴,EF=CE=,
则,
由勾股定理得,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题66
班级 姓名 小组
66.如图,在四边形ABCD中,∠A=∠B=∠BCD=90°,AB=DC=4,AD=BC=8.延长BC到E,使CE=3,连接DE,由直角三角形的性质可知DE=5.动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒.(t>0)
(1)当t=3时,BP= ;
(2)当t= 时,点P运动到∠B的角平分线上;
(3)请用含t的代数式表示△ABP的面积S;
(4)当0<t<6时,直接写出点P到四边形ABED相邻两边距离相等时t的值.
每日一题67
班级 姓名 小组
67.如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连接PE,设点P的运动时间为t秒.
(1)若PE⊥BC,求BQ的长;
(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.
每日一题68
班级 姓名 小组
68.如图所示, ABCD的边AB在x轴上,点D在y轴上,已知OA=3,AD=6,BD⊥AD,从C点出发的点E,以每秒1个单位的速度向点D移动.M是BD的中点,EM的延长线交AB于点F.
(1)求点B,C的坐标;
(2)当四边形EFBC是平行四边形时,求点E的移动时间t(秒).
(3)当△DEM为等腰三角形时,求CE的长.
每日一题69
班级 姓名 小组
69.如图1,四边形ABCD是平行四边形,点E在边AD上,连结BE,过点D作DF∥BE,交BC于点F,点G,H分别是BE,DF的中点,连结EH,GF.
(1)求证:四边形EGFH为平行四边形;
(2)若BC=10,AB=6,∠ABC=60°;
①当BG=GF时,求四边形EGFH的面积;
②如图2,延长FG交AB于点P,连结AG,记△APG的面积为S1,△BPG的面积为S2,若FP⊥AB,求的值.
每日一题70
班级 姓名 小组
70.定义:我们把对角线长度相等的四边形叫做等线四边形.
(1)尝试:如图1,在3×3的正方形网格图形中,已知点A、点B是两个格点,请你作出一个等线四边形,要求A、B是其中两个顶点,且另外两个顶点也是格点;
(2)推理:如图2,已知△AOD与△BOC均为等腰直角三角形,∠AOD=∠BOC=90°,连结AB,CD,求证:四边形ABCD是等线四边形;
(3)拓展:如图3,已知四边形ABCD是等线四边形,对角线AC,BD交于点O,若∠AOD=60°,AB=,BC=,AD=2.求CD的长.
每日一题66参考答案
66.解:(1)BP=2t=2×3=6,故答案为:6;
(2)作∠B的角平分线交AD于F,
∴∠ABF=∠FBC,
∵∠A=∠ABC=∠BCD=90°,∴四边形ABCD是矩形,
∵AD∥BC,∴∠AFB=∠FBC,
∴∠ABF=∠AFB,∴AF=AB=4,
∴DF=AD﹣AF=8﹣4=4,∴BC+CD+DF=8+4+4=16,
∴2t=16,解得t=8.
∴当t=8时,点P运动到∠ABC的角平分线上;故答案为:8;
(3)根据题意分3种情况讨论:
①当点P在BC上运动时,S△ABP=×BP×AB=×2t×4=4t;(0<t<4);
②当点P在CD上运动时,S△ABP=×AB×BC=×4×8=16;(4≤t≤6);
③当点P在AD上运动时,S△ABP=×AB×AP=×4×(20﹣2t)=﹣4t+40;(6<t≤10);
(4)当0<t<6时,点P在BC、CD边上运动,
根据题意分情况讨论:
①当点P在BC上,点P到四边形ABED相邻两边距离相等,
∴点P到AD边的距离为4,∴点P到AB边的距离也为4,即BP=4,
∴2t=4,解得t=2s;
②当点P在BC上,点P到AD边的距离为4,∴点P到DE边的距离也为4,
∴PE=DE=5,∴PC=PE﹣CE=2,∴8﹣2t=2,解得t=3s;
③当点P在CD上,如图,过点P作PH⊥DE于点H,
点P到DE、BE边的距离相等,即PC=PH,
∵PC=2t﹣8,∵S△DCE=S△DPE+S△PCE,
∴3×4=5×PH+3×PC,
∴12=8PH,∴12=8(2t﹣8),解得t=.
综上所述:t=2或t=3或t=时,点P到四边形ABED相邻两边距离相等.
每日一题67 参考答案
67.解:(1)作AM⊥BC于M,设AC交PE于N.如图所示:
∵∠BAC=90°,∠B=45°,∴∠C=45°=∠B,
∴AB=AC,∴BM=CM,∴AM=BC=5,
∵AD∥BC,∴∠PAN=∠C=45°,
∵PE⊥BC,∴PE=AM=5,PE⊥AD,
∴△APN和△CEN是等腰直角三角形,
∴PN=AP=t,CE=NE=5﹣t,
∵CE=CQ﹣QE=2t﹣2,∴5﹣t=2t﹣2,
解得:t=,所以BQ=BC﹣CQ=10﹣2×=;
(2)存在,t=4或12;理由如下:
若以A,B,E,P为顶点的四边形为平行四边形,则AP=BE,
∴t=10﹣2t+2或t=2t﹣2﹣10
解得:t=4或12
∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4或12.
每日一题68 参考答案
68.解:(1)∵OA=3,AD=6,
∴OD=3,
∴∠DAB=60°,
∵BD⊥AD,
∴△ADB是含30°角的直角三角形,
∴AB=2AD=12,
∵四边形ABCD是平行四边形,
∴AB=DC=12,
∴B坐标为(9,0),C坐标为(12,3);
(2)∵M是BD的中点,四边形EFBC是平行四边形,
∴EF∥BC时,点E是CD的中点,
∴CE=6,
∴t=6;
(3)当△DEM为等腰三角形时,①当MD=ME=BD=3时,∠BDC=30°,
∴DE=9,
∴CE=CD﹣DE=12﹣9=3,
②当DM=DE=BD=3时,
∴DE=3,
∴CE=CD﹣DE=12﹣3,
③当ED=EM时,DM=BD=3,
∵∠BDC=30°,
∴DE=3,
∴CE=CD﹣DE=12﹣3=9,
综上所述,当△DEM为等腰三角形时,CE的长为3或9或12﹣3.
每日一题69 参考答案
69.解:(1)如图1,
∵在平行四边形ABCD中,AD∥BC,DF∥BE,
∴四边形BFDE是平行四边形,∴BE=DF,
∵G、H分别是BE、DF的中点,∴EG=FH,
∵EG∥FH,∴四边形EGFH为平行四边形;
(2)①连接EF,
∵BG=GF、BG=EG,∴EG=FG=BG,∴∠1=∠2,∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴∠2+∠4=90°,即∠BFE=90°,
由(1)知,四边形EGFH为平行四边形,
∴S四边形EGFH=2S△EGF=S△BEF,
过点A作AM⊥BC,则EF∥AM,
∵AB=6,∠ABC=60°,
∴AM=3,BM=3,
∵AM∥EF,AE∥MF,∠AMF=90°,
∴四边形AMFE为矩形,
设DE=a,则BF=a,MF=BF﹣BM=a﹣3,AE=AD﹣AE=10﹣a,
∵a﹣3=10﹣a,
∴a=,
∴S四边形EGFH=S△BEF===;
②延长FG交DA的延长线于点N,
∵GE=GB,∠NEG=∠FBG,∠NGE=∠FGB,
∴△EGN≌△BGF(SAS),
∴NE=BF,
假设BP=a,则BF=DE=2a,AE=10﹣2a,AN=4a﹣10,AP=2a﹣5,
由AP+BP=6得a=,
∵△APG与△BPG同高,∴===.
每日一题70 参考答案
【70解:(1)如图1所示,矩形APBQ即为所求.
(2)证明:
如图2,连结AC,BD.
∵△AOD与△BOC均为等腰直角三角形,
∴OA=OD,OC=OB,∠AOD=∠BOC,
∴∠AOC=∠BOD,
∴△AOC≌△DOB(SAS),
∴BD=AC,
∴四边形ABCD是等线四边形.
(3)解:如图3,分别以AD、BC为底作等腰△ADE、等腰△BCE,顶点均为点E.
于是有,EA=ED,EC=EB,
∵AC=BD,
∴△AEC≌△DEB(SSS),
∴∠BDE=∠CAE,
∴∠AED=∠AOD=60°,
∴△AED是等边三角形.
同理,△BCE也是等边三角形.
∴EA=ED=AD=2,.
∵,
∴AE2+BE2=AB2,
∴∠AEB=90°,
∴∠DEC=150°.
过点C作CF⊥DE于交DE延长线于点F,则∠CEF=30°.
∴,EF=CE=,
则,
由勾股定理得,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
