浙教版八年级下册数学每日一题71-75(第五章 特殊平行四边形)培优练习(含解析)
文档属性
| 名称 | 浙教版八年级下册数学每日一题71-75(第五章 特殊平行四边形)培优练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 14:36:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
每日一题71
班级 姓名 小组
71.如图,等腰△ABC中,已知AC=BC=2,AB=4,作∠ACB的外角平分线CF,点E从点B沿着射线BA以每秒2个单位的速度运动,过点E作BC的平行线交CF于点F.
(1)求证:四边形BCFE是平行四边形;
(2)当点E是边AB的中点时,连接AF,试判断四边形AECF的形状,并说明理由;
(3)设运动时间为t秒,是否存在t的值,使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形?不存在的,试说明理由;存在的,请求出t的值.
每日一题72
班级 姓名 小组
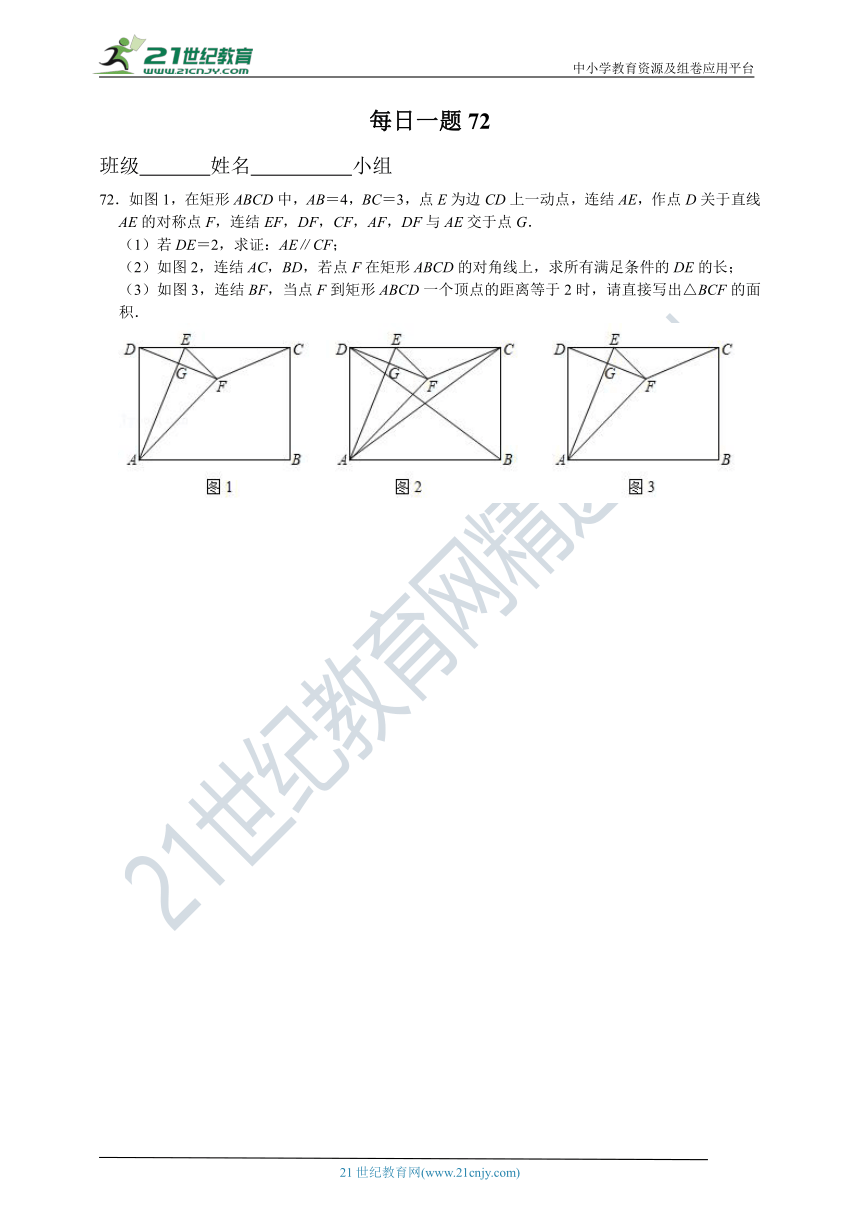
72.如图1,在矩形ABCD中,AB=4,BC=3,点E为边CD上一动点,连结AE,作点D关于直线AE的对称点F,连结EF,DF,CF,AF,DF与AE交于点G.
(1)若DE=2,求证:AE∥CF;
(2)如图2,连结AC,BD,若点F在矩形ABCD的对角线上,求所有满足条件的DE的长;
(3)如图3,连结BF,当点F到矩形ABCD一个顶点的距离等于2时,请直接写出△BCF的面积.
每日一题73
班级 姓名 小组
73.在矩形ABCD中,点P是射线BC上一动点,点B关于直线AP的对称点为E,直线PE与直线CD交于点F.
(1)如图,当A,C、E共线时,若∠ACB=30°,判断△ACF的形状,并证明;
(2)若当点P在线段BC上的某个位置时(不与B,C重合),有∠PAF=45°,求证:当点P在BC延长线上任意位置时,都有∠PAF=45°.
每日一题74
班级 姓名 小组
74.问题:如图,在 ABCD中,AB=8,AD=5,∠DAB,∠ABC的平分线AE,BF分别与直线CD交于点E,F,求EF的长.
答案:EF=2.
探究:(1)把“问题”中的条件“AB=8”去掉,其余条件不变.
①当点E与点F重合时,求AB的长;
②当点E与点C重合时,求EF的长.
(2)把“问题”中的条件“AB=8,AD=5”去掉,其余条件不变,当点C,D,E,F相邻两点间的距离相等时,求的值.
每日一题75
班级 姓名 小组
75.如图,矩形ABCD中,AB=4,点E是边AD的中点,点F是对角线BD上一动点,∠ADB=30°.连结EF,作点D关于直线EF的对称点P.
(1)若EF⊥BD,求DF的长;
(2)若PE⊥BD,求DF的长;
(3)直线PE交BD于点Q,若△DEQ是锐角三角形,求DF长的取值范围.
每日一题71参考答案
【解答】(1)证明:如图1,∵AC=BC,∴∠B=∠BAC,
∵CF平分∠ACH,∴∠ACF=∠FCH,
∵∠ACH=∠B+∠BAC=∠ACF+∠FCH,∴∠FCH=∠B,∴BE∥CF,
∵EF∥BC,∴四边形BCFE是平行四边形;
(2)解:四边形AECF是矩形,理由是:如图2,∵E是AB的中点,AC=BC,
∴CE⊥AB,∴∠AEC=90°,由(1)知:四边形BCFE是平行四边形,∴CF=BE=AE,
∵AE∥CF,∴四边形AECF是矩形;
(3)解:分三种情况:
①以EF和CF两边为邻边所构造的平行四边形恰好是菱形时,如图3,
∴BE=BC,即2t=2,t=;
②以CE和CF两边为邻边所构造的平行四边形恰好是菱形时,如图4,过C作CD⊥AB于D,
∵AC=BC,AB=4,∴BD=2,
由勾股定理得:CD===6,
∵EG2=EC2,即(2t)2=62+(2t﹣2)2,t=5;
③以CE和EF两边为邻边所构造的平行四边形恰好是菱形时,如图5,CA=AF=BC,此时E与A重合,∴t=2,
综上,t的值为秒或5秒或2秒;
故答案为:秒或5秒或2秒.
每日一题72 参考答案
【解答】证明:(1)如图1,∵四边形ABCD为矩形,∴CD=AB=4,
∵DE=2,∴CE=CD﹣DE=2,∴CE=DE=2,
∵D和F关于AE对称,∴DG=FG,∴EG是△DFC的中位线,∴AE∥CF;
解:(2)①如图2,当点F在对角线AC上时,
∵D和F关于AE对称,∴AE垂直平分DF,∴DE=EF,AD=AF=3,
设DE=EF=x,则CE=4﹣x,∵AC==5,∴CF=AC﹣AF=5﹣3=2,
在Rt△EFC中,EF2+CF2=CE2,∴x2+22=(4﹣x)2,∴,∴,
②如图3,当点F在对角线BD上时,
∵四边形ABCD为矩形,∴BD=AC=5,
∵,∴AG=,∴=,
设DE=x,GE=y,∵DG2+GE2=DE2,∴①,
∵,∴②,
联立①②得,
,解得x=,∴,∴或;
(3)①当F点到A点距离为2时,∵AF=AD=3>2,∴此种情况不存在,
②当F点到B点距离为2时,连接FB,则FB=2,AF=AD=3,
过F作FH⊥AB于H,FQ⊥BC于Q,如图4,∴∠FHB=∠ABC=∠BQF=90°,
∴四边形FHBQ为矩形,∴FQ=BH,设BH=x,则AH=4﹣x,
∵FH2=AF2﹣FH2=FB2﹣BH2,∴4﹣x2=9﹣(4﹣x)2,∴,∴,
∴S△BCF==,
③当点F到C点距离为2时,如图5,连接BF,则FC=2,
∵AF+FC≥AC,又AF+FC=5,AC=5,∴AF+FC=AC,∴A,C,F三点共线,
即F在线段AC上,∵==,∴S△BCF===;
④当点F到D点距离为2时,如图6,连接BF,
则DF=2,∴DG=GF=1,∴AG==,
∵S△ADF=,∴MF=,∴NF=MN﹣MF=4,
∴S△BCF==,
即当点F到矩形ABC顶点B的距离等于2时,△BCF的面积为,
当点F到矩形ABC顶点C的距离等于2时,△BCF的面积为,
当点F到矩形ABC顶点D的距离等于2时,△BCF的面积为.
每日一题73参考答案
【解答】(1)解:△ACF为等边三角形,理由如下:
∵四边形ABCD为矩形,∠ACB=30°,∴∠ACD=60°,
即∠ACF=60°,在Rt△ABC中,∠ACB=30°,∴AB=AC,
∵点B关于直线AP的对称点为E,∴AB=AE,∠AEP=90°,∴AE=AC,
即点E为AC中点,∴FP为线段AC的垂直平分线,
∴AF=CF,∴△ACF为等边三角形;
(2)解:当点P在线段BC上时,如图,
∵∠PAF=45°,∴∠EAF=45°﹣∠PAE,
∵∠BAD=90°,∴∠FAD=45°﹣∠PAB,∴∠EAF=∠FAD,
∵点B关于直线AP的对称点为E,∴∠ABP=∠AEP=90°,AB=AE,
在△EAF和△DAF中,
,∴△EAF≌△DAF(AAS),∴AD=AE,∴AB=AD,
即矩形ABCD为正方形,
当点P在线段BC延长线上时,如图,
∵矩形ABCD为正方形,∴AD=AE,∠ADF=∠AEF=90°,
在Rt△ADF和Rt△AEF中,
,∴Rt△ADF≌Rt△AEF(HL),∴∠DAF=∠EAF,
设∠DAF=α,∠PAD=β,则∠EAF=α,∴∠PAE=2α+β,
∵∠PAE=∠PAB,∴∠PAB=2α+β,
∵∠PAB+∠PAD=90°,∴2α+β+β=90°,∴α+β=45°,
∴∠PAF=α+β=45°.
每日一题74 参考答案
解:(1)①如图1所示:
∵四边形ABCD是平行四边形,∴CD=AB=8,BC=AD=5,AB∥CD,∴∠DEA=∠BAE,
∵AE平分∠DAB,∴∠DAE=∠BAE,∴∠DEA=∠DAE,∴DE=AD=5,
同理:BC=CF=5,∵点E与点F重合,∴AB=CD=DE+CF=10;
②如图2所示:
∵点E与点C重合,∴DE=DC=5,∵CF=BC=5,∴点F与点D重合,∴EF=DC=5.
(2)分三种情况:
①如图3所示:
同(1)得:AD=DE,∵点C,D,E,F相邻两点间的距离相等,∴AD=DE=EF=CF,∴;
②如图4所示:
同(1)得:AD=DE=CF,∵DF=FE=CE,∴;
③如图5所示:
同(1)得:AD=DE=CF,∵DF=DC=CE,∴2;
综上所述,的值为或或2.
每日一题75 参考答案
解:(1)∵点D、点P关于直线EF的对称,EF⊥BD,∴点P在BD上,
∵四边形ABCD是矩形,∴∠BAD=90°,∵AB=4,∠ADB=30°.∴AD=4,
∵点E是边AD的中点,∴DE=2,∵EF⊥BD,∴DF=3.
(2)①如图2,
∵PE⊥BD,∠ADB=30°.∴∠PED=60°,
由对称可得,EF平分∠PED,∴∠DEF=∠PEF=30°,
∴△DEF是等腰三角形,∴DF=EF,∵PE⊥BD,∠ADB=30°.DE=2,∴QE,
∵∠PEF=30°,∴EF=2,∴DF=EF=2;
②如图3,
∵PE⊥BD,∠ADB=30°.∴∠PED=120°,
由对称可得,PF=DF,EP=ED,EF平分∠PED,∴∠DEF=∠PEF=120°,∴∠EFD=30°,
∴△DEF是等腰三角形,
∵PE⊥BD,∴QD=QFDF,∵PE⊥BD,∠ADB=30°.DE=2,
∴QE,QD=3∴DF=2QD=6;∴DF的长为2或6.
(3)由(2)得,当∠DQE=90°时,DF=2(如图2)或6(如图3),
当∠DEQ=90°时,
第一种情况,如图4,
∵EF平分∠PED,∴∠DEF=45°,
过点F作FM⊥AD于点M,设EM=a,则FM=a,DMa,
∴a+a=2,∴a=3,DF=6﹣2,∴2<DF<6﹣2;
第二种情况,如图5,
∵EF平分∠AEQ,∴∠MEF=45°,
过点F作FM⊥AD于点M,设EM=a,则FM=a,DMa,∴a﹣a=2,∴a=3,DF=6+2,
∵6+28,∴DF最大值为8,∴6<DF≤8.
综上,DF长的取值范围为2<DF<6﹣2或6<DF≤8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题71
班级 姓名 小组
71.如图,等腰△ABC中,已知AC=BC=2,AB=4,作∠ACB的外角平分线CF,点E从点B沿着射线BA以每秒2个单位的速度运动,过点E作BC的平行线交CF于点F.
(1)求证:四边形BCFE是平行四边形;
(2)当点E是边AB的中点时,连接AF,试判断四边形AECF的形状,并说明理由;
(3)设运动时间为t秒,是否存在t的值,使得以△EFC的其中两边为邻边所构造的平行四边形恰好是菱形?不存在的,试说明理由;存在的,请求出t的值.
每日一题72
班级 姓名 小组
72.如图1,在矩形ABCD中,AB=4,BC=3,点E为边CD上一动点,连结AE,作点D关于直线AE的对称点F,连结EF,DF,CF,AF,DF与AE交于点G.
(1)若DE=2,求证:AE∥CF;
(2)如图2,连结AC,BD,若点F在矩形ABCD的对角线上,求所有满足条件的DE的长;
(3)如图3,连结BF,当点F到矩形ABCD一个顶点的距离等于2时,请直接写出△BCF的面积.
每日一题73
班级 姓名 小组
73.在矩形ABCD中,点P是射线BC上一动点,点B关于直线AP的对称点为E,直线PE与直线CD交于点F.
(1)如图,当A,C、E共线时,若∠ACB=30°,判断△ACF的形状,并证明;
(2)若当点P在线段BC上的某个位置时(不与B,C重合),有∠PAF=45°,求证:当点P在BC延长线上任意位置时,都有∠PAF=45°.
每日一题74
班级 姓名 小组
74.问题:如图,在 ABCD中,AB=8,AD=5,∠DAB,∠ABC的平分线AE,BF分别与直线CD交于点E,F,求EF的长.
答案:EF=2.
探究:(1)把“问题”中的条件“AB=8”去掉,其余条件不变.
①当点E与点F重合时,求AB的长;
②当点E与点C重合时,求EF的长.
(2)把“问题”中的条件“AB=8,AD=5”去掉,其余条件不变,当点C,D,E,F相邻两点间的距离相等时,求的值.
每日一题75
班级 姓名 小组
75.如图,矩形ABCD中,AB=4,点E是边AD的中点,点F是对角线BD上一动点,∠ADB=30°.连结EF,作点D关于直线EF的对称点P.
(1)若EF⊥BD,求DF的长;
(2)若PE⊥BD,求DF的长;
(3)直线PE交BD于点Q,若△DEQ是锐角三角形,求DF长的取值范围.
每日一题71参考答案
【解答】(1)证明:如图1,∵AC=BC,∴∠B=∠BAC,
∵CF平分∠ACH,∴∠ACF=∠FCH,
∵∠ACH=∠B+∠BAC=∠ACF+∠FCH,∴∠FCH=∠B,∴BE∥CF,
∵EF∥BC,∴四边形BCFE是平行四边形;
(2)解:四边形AECF是矩形,理由是:如图2,∵E是AB的中点,AC=BC,
∴CE⊥AB,∴∠AEC=90°,由(1)知:四边形BCFE是平行四边形,∴CF=BE=AE,
∵AE∥CF,∴四边形AECF是矩形;
(3)解:分三种情况:
①以EF和CF两边为邻边所构造的平行四边形恰好是菱形时,如图3,
∴BE=BC,即2t=2,t=;
②以CE和CF两边为邻边所构造的平行四边形恰好是菱形时,如图4,过C作CD⊥AB于D,
∵AC=BC,AB=4,∴BD=2,
由勾股定理得:CD===6,
∵EG2=EC2,即(2t)2=62+(2t﹣2)2,t=5;
③以CE和EF两边为邻边所构造的平行四边形恰好是菱形时,如图5,CA=AF=BC,此时E与A重合,∴t=2,
综上,t的值为秒或5秒或2秒;
故答案为:秒或5秒或2秒.
每日一题72 参考答案
【解答】证明:(1)如图1,∵四边形ABCD为矩形,∴CD=AB=4,
∵DE=2,∴CE=CD﹣DE=2,∴CE=DE=2,
∵D和F关于AE对称,∴DG=FG,∴EG是△DFC的中位线,∴AE∥CF;
解:(2)①如图2,当点F在对角线AC上时,
∵D和F关于AE对称,∴AE垂直平分DF,∴DE=EF,AD=AF=3,
设DE=EF=x,则CE=4﹣x,∵AC==5,∴CF=AC﹣AF=5﹣3=2,
在Rt△EFC中,EF2+CF2=CE2,∴x2+22=(4﹣x)2,∴,∴,
②如图3,当点F在对角线BD上时,
∵四边形ABCD为矩形,∴BD=AC=5,
∵,∴AG=,∴=,
设DE=x,GE=y,∵DG2+GE2=DE2,∴①,
∵,∴②,
联立①②得,
,解得x=,∴,∴或;
(3)①当F点到A点距离为2时,∵AF=AD=3>2,∴此种情况不存在,
②当F点到B点距离为2时,连接FB,则FB=2,AF=AD=3,
过F作FH⊥AB于H,FQ⊥BC于Q,如图4,∴∠FHB=∠ABC=∠BQF=90°,
∴四边形FHBQ为矩形,∴FQ=BH,设BH=x,则AH=4﹣x,
∵FH2=AF2﹣FH2=FB2﹣BH2,∴4﹣x2=9﹣(4﹣x)2,∴,∴,
∴S△BCF==,
③当点F到C点距离为2时,如图5,连接BF,则FC=2,
∵AF+FC≥AC,又AF+FC=5,AC=5,∴AF+FC=AC,∴A,C,F三点共线,
即F在线段AC上,∵==,∴S△BCF===;
④当点F到D点距离为2时,如图6,连接BF,
则DF=2,∴DG=GF=1,∴AG==,
∵S△ADF=,∴MF=,∴NF=MN﹣MF=4,
∴S△BCF==,
即当点F到矩形ABC顶点B的距离等于2时,△BCF的面积为,
当点F到矩形ABC顶点C的距离等于2时,△BCF的面积为,
当点F到矩形ABC顶点D的距离等于2时,△BCF的面积为.
每日一题73参考答案
【解答】(1)解:△ACF为等边三角形,理由如下:
∵四边形ABCD为矩形,∠ACB=30°,∴∠ACD=60°,
即∠ACF=60°,在Rt△ABC中,∠ACB=30°,∴AB=AC,
∵点B关于直线AP的对称点为E,∴AB=AE,∠AEP=90°,∴AE=AC,
即点E为AC中点,∴FP为线段AC的垂直平分线,
∴AF=CF,∴△ACF为等边三角形;
(2)解:当点P在线段BC上时,如图,
∵∠PAF=45°,∴∠EAF=45°﹣∠PAE,
∵∠BAD=90°,∴∠FAD=45°﹣∠PAB,∴∠EAF=∠FAD,
∵点B关于直线AP的对称点为E,∴∠ABP=∠AEP=90°,AB=AE,
在△EAF和△DAF中,
,∴△EAF≌△DAF(AAS),∴AD=AE,∴AB=AD,
即矩形ABCD为正方形,
当点P在线段BC延长线上时,如图,
∵矩形ABCD为正方形,∴AD=AE,∠ADF=∠AEF=90°,
在Rt△ADF和Rt△AEF中,
,∴Rt△ADF≌Rt△AEF(HL),∴∠DAF=∠EAF,
设∠DAF=α,∠PAD=β,则∠EAF=α,∴∠PAE=2α+β,
∵∠PAE=∠PAB,∴∠PAB=2α+β,
∵∠PAB+∠PAD=90°,∴2α+β+β=90°,∴α+β=45°,
∴∠PAF=α+β=45°.
每日一题74 参考答案
解:(1)①如图1所示:
∵四边形ABCD是平行四边形,∴CD=AB=8,BC=AD=5,AB∥CD,∴∠DEA=∠BAE,
∵AE平分∠DAB,∴∠DAE=∠BAE,∴∠DEA=∠DAE,∴DE=AD=5,
同理:BC=CF=5,∵点E与点F重合,∴AB=CD=DE+CF=10;
②如图2所示:
∵点E与点C重合,∴DE=DC=5,∵CF=BC=5,∴点F与点D重合,∴EF=DC=5.
(2)分三种情况:
①如图3所示:
同(1)得:AD=DE,∵点C,D,E,F相邻两点间的距离相等,∴AD=DE=EF=CF,∴;
②如图4所示:
同(1)得:AD=DE=CF,∵DF=FE=CE,∴;
③如图5所示:
同(1)得:AD=DE=CF,∵DF=DC=CE,∴2;
综上所述,的值为或或2.
每日一题75 参考答案
解:(1)∵点D、点P关于直线EF的对称,EF⊥BD,∴点P在BD上,
∵四边形ABCD是矩形,∴∠BAD=90°,∵AB=4,∠ADB=30°.∴AD=4,
∵点E是边AD的中点,∴DE=2,∵EF⊥BD,∴DF=3.
(2)①如图2,
∵PE⊥BD,∠ADB=30°.∴∠PED=60°,
由对称可得,EF平分∠PED,∴∠DEF=∠PEF=30°,
∴△DEF是等腰三角形,∴DF=EF,∵PE⊥BD,∠ADB=30°.DE=2,∴QE,
∵∠PEF=30°,∴EF=2,∴DF=EF=2;
②如图3,
∵PE⊥BD,∠ADB=30°.∴∠PED=120°,
由对称可得,PF=DF,EP=ED,EF平分∠PED,∴∠DEF=∠PEF=120°,∴∠EFD=30°,
∴△DEF是等腰三角形,
∵PE⊥BD,∴QD=QFDF,∵PE⊥BD,∠ADB=30°.DE=2,
∴QE,QD=3∴DF=2QD=6;∴DF的长为2或6.
(3)由(2)得,当∠DQE=90°时,DF=2(如图2)或6(如图3),
当∠DEQ=90°时,
第一种情况,如图4,
∵EF平分∠PED,∴∠DEF=45°,
过点F作FM⊥AD于点M,设EM=a,则FM=a,DMa,
∴a+a=2,∴a=3,DF=6﹣2,∴2<DF<6﹣2;
第二种情况,如图5,
∵EF平分∠AEQ,∴∠MEF=45°,
过点F作FM⊥AD于点M,设EM=a,则FM=a,DMa,∴a﹣a=2,∴a=3,DF=6+2,
∵6+28,∴DF最大值为8,∴6<DF≤8.
综上,DF长的取值范围为2<DF<6﹣2或6<DF≤8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
