浙教版八年级下册数学每日一题76-80(第五章 特殊平行四边形)培优练习(含解析)
文档属性
| 名称 | 浙教版八年级下册数学每日一题76-80(第五章 特殊平行四边形)培优练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 14:37:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
每日一题76
班级 姓名 小组
76.[操作发现]如图1,两张正方形纸片ABCD和CEFG拼在一起,B,C,E三点共线,且EF=AB=1.在BC上截取BH=CE,沿AH,FH分别剪一刀,△ABH平移至△IGF,△HEF平移至△ADI,则可以割补成大正方形AHFI.试求大正方形AHFI的边长.
[类比探究]如图2,两张矩形纸片ABCD和CEFG拼在一起,B,C,E三点共线,且EF=AB=a,CE=BC=b,仿照[操作发现]的方法,把它割补成一个 AHFI,在图2中画出 AHFI,并求出当 AHFI为菱形时a,b应满足的关系式.
[拓展应用]如图3,两张平行四边形纸片ABCD和CEFG拼在一起,B,C,E三点共线,且∠B=60°,其他条件与[类比探究]相同,若割补得到的 AHFI面积是10,求b关于a的函数表达式.
每日一题77
班级 姓名 小组
77.在平行四边形ABCD中,∠ADC的平分线交BC于点E.交AB的延长线于点F,连接AC.
(1)如图1,若∠ADC=90°,G是EF的中点,连接AG、CG.
①求证:BE=BF;
②请判断△AGC的形状,并说明理由.
(2)如图2,若∠ADC=60°,将线段FB绕点F顺时针旋转60°至FG,连接AG、CG,请判断△AGC的形状,并说明理由.
(3)如图3,∠ADC=90°,作∠BED的角平分线EH交AB于点H,已知AB=9,BH=2AH,求BC的长.
每日一题78
班级 姓名 小组
78.如图,在矩形ABCD中,已知AB=4,BC=2,E为AB的中点,设点P是∠DAB平分线上的一个动点(不与点A重合).
(1)证明:PD=PE.
(2)连接PC,求PC的最小值.
(3)设点O是矩形ABCD的对称中心,是否存在点P,使∠DPO=90°?若存在,请直接写出AP的长.
每日一题79
班级 姓名 小组
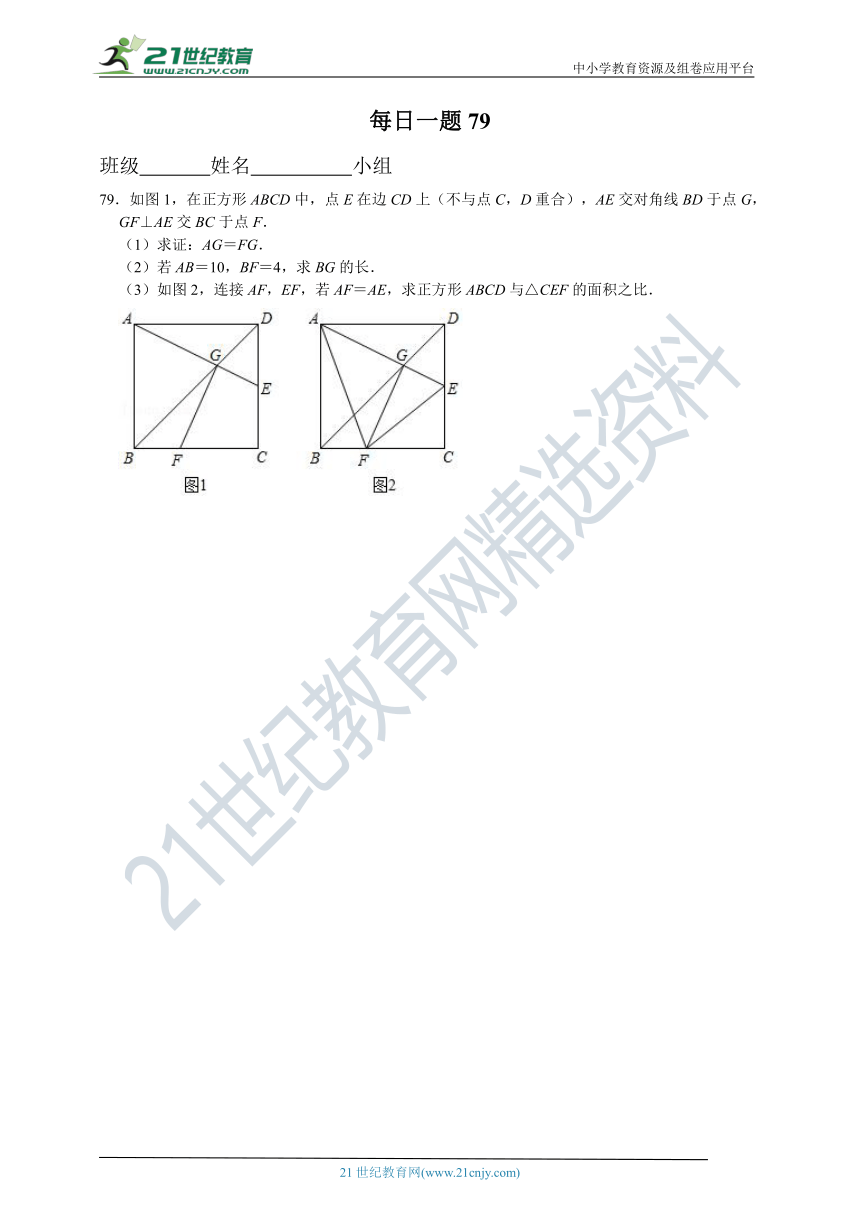
79.如图1,在正方形ABCD中,点E在边CD上(不与点C,D重合),AE交对角线BD于点G,GF⊥AE交BC于点F.
(1)求证:AG=FG.
(2)若AB=10,BF=4,求BG的长.
(3)如图2,连接AF,EF,若AF=AE,求正方形ABCD与△CEF的面积之比.
每日一题80
班级 姓名 小组
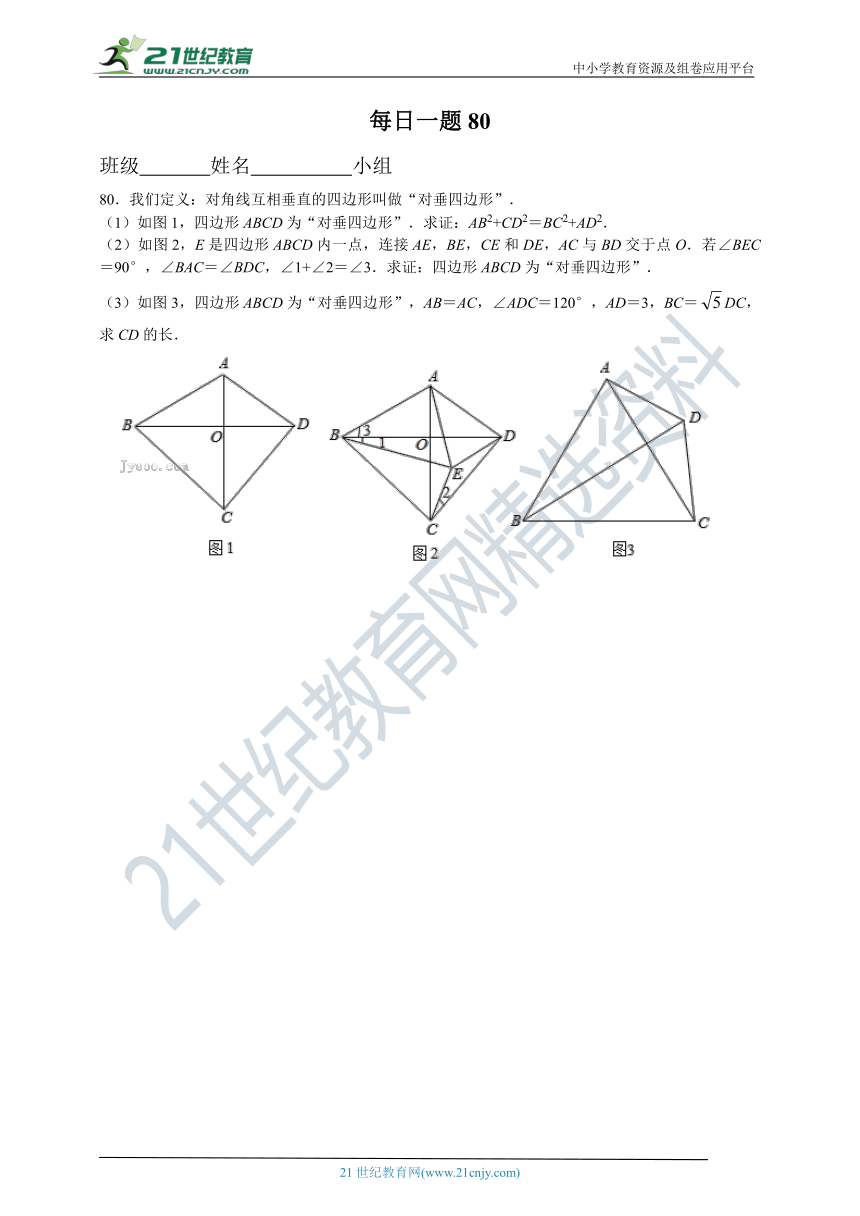
80.我们定义:对角线互相垂直的四边形叫做“对垂四边形”.
(1)如图1,四边形ABCD为“对垂四边形”.求证:AB2+CD2=BC2+AD2.
(2)如图2,E是四边形ABCD内一点,连接AE,BE,CE和DE,AC与BD交于点O.若∠BEC=90°,∠BAC=∠BDC,∠1+∠2=∠3.求证:四边形ABCD为“对垂四边形”.
(3)如图3,四边形ABCD为“对垂四边形”,AB=AC,∠ADC=120°,AD=3,BC=DC,求CD的长.
每日一题76 参考答案
【解答】[操作发现]解:∵EF=AB=1,∴AB=3,
∴S正方形ABCD=AB2=9,S正方形CEFG=EF2=1,
∵四边形ABCD是正方形,∴∠B=90°,∴AH2=AB2+BH2,
∵BH=CE,∴AH2=AB2+CE2,
∴S正方形AHFI=AH2=S正方形ABCD+S正方形CEFG=9+1=10,∴AH=,
即大正方形AHFI的边长为;
[类比探究]解:如图2所示:由剪切与拼接可知,AI∥FH,AI=FH,
∴四边形AHFI是平行四边形,
当 AHFI为菱形时,AH=FH,由题意可知,EF=AB=a,CE=BC=b,
∴AB=3a,BC=3b,
∵BH=CE=b,∴EH=3b,
在Rt△EHF中,FH2=EH2+EF2=9b2+a2,
同理,在Rt△ABH中,AH2=9a2+b2,∴9b2+a2=9a2+b2,∴a=b;
[拓展应用]解:由[操作发现]可知,S平行四边形AHFI=S平行四边形ABCD+S平行四边形CEFG=10,
过A作AM⊥BC于M,如图3所示:则∠AMB=90°,
∵∠B=60°,∴∠BAM=30°,
由题意可知,EF=AB=a,CE=BC=b,∴AB=3a,BC=3b,
∴BM=AB=a,AM=BM=a,
∴S平行四边形ABCD=BC AM=3b×a=ab,
同理:S平行四边形CEFG=ab,∴ab+ab=10,∴ab=2,
∴b关于a的函数表达式为b=.
每日一题77 参考答案
【解答】(1)证明:①∵四边形ABCD是平行四边形,∠ADC=90°,∴四边形ABCD是矩形,
∴∠ABC=90°,AB∥DC,AD∥BC,∴∠F=∠FDC,∠BEF=∠ADF,
∵DF是∠ADC的平分线,∴∠ADF=∠FDC,∴∠F=∠BEF,∴BF=BE;
②△AGC是等腰直角三角形.理由如下:如图1,连接BG,
由①知,BF=BE,∠FBC=90°,∴∠F=∠BEF=45°,
∵G是EF的中点,∴BG=FG,∠F=∠CBG=45°,
∵∠FAD=90°,∴AF=AD,又∵AD=BC,∴AF=BC,
在△AFG和△CBG中,
,∴△AFG≌△CBG(SAS),∴AG=CG,
∴∠FAG=∠BCG,又∵∠FAG+∠GAC+∠ACB=90°,
∴∠BCG+∠GAC+∠ACB=90°,即∠GAC+∠ACG=90°,∴∠AGC=90°,
∴△AGC是等腰直角三角形;
(2)如图2,连接BG,
∵FB绕点F顺时针旋转60°至FG,∴FB=FG,∠BFG=60°,∴△BFG是等边三角形,
∴FG=BG,∠FBG=60°,
又∵四边形ABCD是平行四边形,∠ADC=60°,∴∠ABC=∠ADC=60°
∴∠CBG=180°﹣∠FBG﹣∠ABC=180°﹣60°﹣60°=60°,∴∠AFG=∠CBG,
∵DF是∠ADC的平分线,∴∠ADF=∠FDC,
∵AB∥DC,∴∠AFD=∠FDC,∴∠AFD=∠ADF,∴AF=AD,
在△AFG和△CBG中,
,∴△AFG≌△CBG(SAS),∴AG=CG,∠FAG=∠BCG,
在△ABC中,∠GAC+∠ACG=∠ACB+∠BCG+∠GAC=∠ACB+∠BAG+∠GAC=∠ACB+∠BAC=180°﹣60°=120°,
∴∠AGC=180°﹣(∠GAC+∠ACG)=180°﹣120°=60°,∴△AGC是等边三角形;
(3)如图3,在BH上截取BN=BE,连接NE,∵AB=9,BH=2AH,∴AH=3,BH=6,
∵∠BEF=45°,∴∠BED=135°,∵EH平分∠BED,∴∠BEH=67.5°,∴∠BHE=22.5°,
∵BE=BN,∠ABC=90°,∴∠BEN=∠BNE=45°,NE=BN,
∵∠BNE=∠BHE+∠HNE=45°,∴∠BHE=∠NEH=22.5°,∴HN=NE=BN,
∵BH=BN+NH=(+1)BN=6,∴BN=6﹣6=BE,∴BF=6﹣6,
∴BC=AD=AF=AB+BF=9+6﹣6=6+3
每日一题78 参考答案
【解答】(1)证明:∵四边形ABCD为矩形,
∴∠DAB=90°,
∵AP平分∠DAB,
∴∠DAP=∠EAP=45°,
在△DAP和△EAP中,
,
∴△DAP≌△EAP(SAS)
∴PD=PE;
(2)解:如图1,作CP′⊥AP′于P′,则P′C最小,
∵AB∥CD,∴∠DFA=∠EAP,
∵∠DAP=∠EAP,∴∠DAP=∠DFA=45°,
∴FC=DF=AD=2,∠P′FC=45°,
∴P′C=FC×=,∴PC的最小值为;
(3)解:如图2,∵DF=FC,OA=OC,∴OF∥AD,
∴∠DFO=180°﹣∠ADF=90°,
∴当点P与点F重合时,∠DPO=90°,此时,AP==2,
当点P在AF上时,作PG⊥AD于G,PH⊥AB于H,
∵AP平分∠DAB,PG⊥AD,PH⊥AB,
∴PG=PH,
设PG=PH=a,
由勾股定理得,DP2=(2﹣a)2+a2,OP2=(2﹣a)2+(1﹣a)2,OD2=5,
当∠DPO=90°时,DP2+OP2=OD2,即(2﹣a)2+a2+(2﹣a)2+(1﹣a)2=5,
解得,a1=2(舍去),a2=,当a=时,AP=,
综上所述,∠DPO=90°时,AP=2或.
每日一题79 参考答案
【解答】证明:(1)连接GC,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,∠ABD=∠CBD=45°,
又∵BG=BG,∴△ABG≌△CBG(SAS),
∴AG=CG,∠BAG=∠BCG,
∵∠ABC+∠BAG+∠AGF+∠BFG=360°,且∠ABC=∠AGF=90°,
∴∠BAG+∠BFG=180°,
∴∠BCG+∠BFG=180°,
∵∠BFG+∠GFC=180°,
∴∠BCG=∠GFC,
∴GC=GF,
∴AG=FG;
(2)如图2,过点G作GH⊥BC于H,
∵AB=10,BF=4,
∴AF2=AB2+BF2=AG2+GF2,
∴GF2=58,
∵∠DBC=45°,GH⊥BC,
∴BH=GH,BG=GH,
∵GF2=GH2+FH2,
∴58=GH2+(GH﹣4)2,
∴GH=7,(负值舍去),
∴BG=7;
(3)如图,在AB上截取BF=BN,连接NF,
∵AG=GF,AG⊥GF,∴∠EAF=45°,
∵AE=AF,AB=AD,∴Rt△ABF≌Rt△ADE(HL),
∴∠BAF=∠DAE=22.5°,BF=DE,∴CF=CE,
∵BF=BN,∠ABC=90°,∴NF=BF,∠BNF=∠BFN=45°,
∴∠BAF=∠AFN=22.5°,∴AN=NF=BF,
∵AB=BC,∴BN+AN=BF+FC,∴FC=BF,∴BC=(+1)BF,
∴正方形ABCD与△CEF的面积之比=BC2:FC2=3+2:1.
每日一题80 参考答案
【解答】证明:(1)∵四边形ABCD为“对垂四边形”,
∴AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AB2+CD2=AD2+BC2;
(2)∵∠BAC=∠BDC,∠AOB=∠COD,
∴∠3=∠ACD,
∵∠3=∠1+∠2,∠ACD=∠ACE+∠2,
∴∠1=∠ACE,
∴∠BOC=∠BEC=90°,
∴AC⊥BD,
∴四边形ABCD为“对垂四边形”;
(3)过点A作AH⊥DC,交CD延长线于点H,
设CD=x,则BC=DC=x,
∵四边形ABCD为“对垂四边形”,AD=3,
∴AB2+CD2=AD2+BC2,
∴AB2=9+5x2﹣x2=9+4x2,
∵AB=AC,
∴AC2=9+4x2,
∵∠ADC=120°,
∴∠ADH=60°,∠DAH=30°,
∴DH=AD=,AH=DH=,
∵AC2=AH2+CH2,
∴9+4x2=+(x+)2,
∴x1=0(舍去),x2=1,
∴CD的长度1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题76
班级 姓名 小组
76.[操作发现]如图1,两张正方形纸片ABCD和CEFG拼在一起,B,C,E三点共线,且EF=AB=1.在BC上截取BH=CE,沿AH,FH分别剪一刀,△ABH平移至△IGF,△HEF平移至△ADI,则可以割补成大正方形AHFI.试求大正方形AHFI的边长.
[类比探究]如图2,两张矩形纸片ABCD和CEFG拼在一起,B,C,E三点共线,且EF=AB=a,CE=BC=b,仿照[操作发现]的方法,把它割补成一个 AHFI,在图2中画出 AHFI,并求出当 AHFI为菱形时a,b应满足的关系式.
[拓展应用]如图3,两张平行四边形纸片ABCD和CEFG拼在一起,B,C,E三点共线,且∠B=60°,其他条件与[类比探究]相同,若割补得到的 AHFI面积是10,求b关于a的函数表达式.
每日一题77
班级 姓名 小组
77.在平行四边形ABCD中,∠ADC的平分线交BC于点E.交AB的延长线于点F,连接AC.
(1)如图1,若∠ADC=90°,G是EF的中点,连接AG、CG.
①求证:BE=BF;
②请判断△AGC的形状,并说明理由.
(2)如图2,若∠ADC=60°,将线段FB绕点F顺时针旋转60°至FG,连接AG、CG,请判断△AGC的形状,并说明理由.
(3)如图3,∠ADC=90°,作∠BED的角平分线EH交AB于点H,已知AB=9,BH=2AH,求BC的长.
每日一题78
班级 姓名 小组
78.如图,在矩形ABCD中,已知AB=4,BC=2,E为AB的中点,设点P是∠DAB平分线上的一个动点(不与点A重合).
(1)证明:PD=PE.
(2)连接PC,求PC的最小值.
(3)设点O是矩形ABCD的对称中心,是否存在点P,使∠DPO=90°?若存在,请直接写出AP的长.
每日一题79
班级 姓名 小组
79.如图1,在正方形ABCD中,点E在边CD上(不与点C,D重合),AE交对角线BD于点G,GF⊥AE交BC于点F.
(1)求证:AG=FG.
(2)若AB=10,BF=4,求BG的长.
(3)如图2,连接AF,EF,若AF=AE,求正方形ABCD与△CEF的面积之比.
每日一题80
班级 姓名 小组
80.我们定义:对角线互相垂直的四边形叫做“对垂四边形”.
(1)如图1,四边形ABCD为“对垂四边形”.求证:AB2+CD2=BC2+AD2.
(2)如图2,E是四边形ABCD内一点,连接AE,BE,CE和DE,AC与BD交于点O.若∠BEC=90°,∠BAC=∠BDC,∠1+∠2=∠3.求证:四边形ABCD为“对垂四边形”.
(3)如图3,四边形ABCD为“对垂四边形”,AB=AC,∠ADC=120°,AD=3,BC=DC,求CD的长.
每日一题76 参考答案
【解答】[操作发现]解:∵EF=AB=1,∴AB=3,
∴S正方形ABCD=AB2=9,S正方形CEFG=EF2=1,
∵四边形ABCD是正方形,∴∠B=90°,∴AH2=AB2+BH2,
∵BH=CE,∴AH2=AB2+CE2,
∴S正方形AHFI=AH2=S正方形ABCD+S正方形CEFG=9+1=10,∴AH=,
即大正方形AHFI的边长为;
[类比探究]解:如图2所示:由剪切与拼接可知,AI∥FH,AI=FH,
∴四边形AHFI是平行四边形,
当 AHFI为菱形时,AH=FH,由题意可知,EF=AB=a,CE=BC=b,
∴AB=3a,BC=3b,
∵BH=CE=b,∴EH=3b,
在Rt△EHF中,FH2=EH2+EF2=9b2+a2,
同理,在Rt△ABH中,AH2=9a2+b2,∴9b2+a2=9a2+b2,∴a=b;
[拓展应用]解:由[操作发现]可知,S平行四边形AHFI=S平行四边形ABCD+S平行四边形CEFG=10,
过A作AM⊥BC于M,如图3所示:则∠AMB=90°,
∵∠B=60°,∴∠BAM=30°,
由题意可知,EF=AB=a,CE=BC=b,∴AB=3a,BC=3b,
∴BM=AB=a,AM=BM=a,
∴S平行四边形ABCD=BC AM=3b×a=ab,
同理:S平行四边形CEFG=ab,∴ab+ab=10,∴ab=2,
∴b关于a的函数表达式为b=.
每日一题77 参考答案
【解答】(1)证明:①∵四边形ABCD是平行四边形,∠ADC=90°,∴四边形ABCD是矩形,
∴∠ABC=90°,AB∥DC,AD∥BC,∴∠F=∠FDC,∠BEF=∠ADF,
∵DF是∠ADC的平分线,∴∠ADF=∠FDC,∴∠F=∠BEF,∴BF=BE;
②△AGC是等腰直角三角形.理由如下:如图1,连接BG,
由①知,BF=BE,∠FBC=90°,∴∠F=∠BEF=45°,
∵G是EF的中点,∴BG=FG,∠F=∠CBG=45°,
∵∠FAD=90°,∴AF=AD,又∵AD=BC,∴AF=BC,
在△AFG和△CBG中,
,∴△AFG≌△CBG(SAS),∴AG=CG,
∴∠FAG=∠BCG,又∵∠FAG+∠GAC+∠ACB=90°,
∴∠BCG+∠GAC+∠ACB=90°,即∠GAC+∠ACG=90°,∴∠AGC=90°,
∴△AGC是等腰直角三角形;
(2)如图2,连接BG,
∵FB绕点F顺时针旋转60°至FG,∴FB=FG,∠BFG=60°,∴△BFG是等边三角形,
∴FG=BG,∠FBG=60°,
又∵四边形ABCD是平行四边形,∠ADC=60°,∴∠ABC=∠ADC=60°
∴∠CBG=180°﹣∠FBG﹣∠ABC=180°﹣60°﹣60°=60°,∴∠AFG=∠CBG,
∵DF是∠ADC的平分线,∴∠ADF=∠FDC,
∵AB∥DC,∴∠AFD=∠FDC,∴∠AFD=∠ADF,∴AF=AD,
在△AFG和△CBG中,
,∴△AFG≌△CBG(SAS),∴AG=CG,∠FAG=∠BCG,
在△ABC中,∠GAC+∠ACG=∠ACB+∠BCG+∠GAC=∠ACB+∠BAG+∠GAC=∠ACB+∠BAC=180°﹣60°=120°,
∴∠AGC=180°﹣(∠GAC+∠ACG)=180°﹣120°=60°,∴△AGC是等边三角形;
(3)如图3,在BH上截取BN=BE,连接NE,∵AB=9,BH=2AH,∴AH=3,BH=6,
∵∠BEF=45°,∴∠BED=135°,∵EH平分∠BED,∴∠BEH=67.5°,∴∠BHE=22.5°,
∵BE=BN,∠ABC=90°,∴∠BEN=∠BNE=45°,NE=BN,
∵∠BNE=∠BHE+∠HNE=45°,∴∠BHE=∠NEH=22.5°,∴HN=NE=BN,
∵BH=BN+NH=(+1)BN=6,∴BN=6﹣6=BE,∴BF=6﹣6,
∴BC=AD=AF=AB+BF=9+6﹣6=6+3
每日一题78 参考答案
【解答】(1)证明:∵四边形ABCD为矩形,
∴∠DAB=90°,
∵AP平分∠DAB,
∴∠DAP=∠EAP=45°,
在△DAP和△EAP中,
,
∴△DAP≌△EAP(SAS)
∴PD=PE;
(2)解:如图1,作CP′⊥AP′于P′,则P′C最小,
∵AB∥CD,∴∠DFA=∠EAP,
∵∠DAP=∠EAP,∴∠DAP=∠DFA=45°,
∴FC=DF=AD=2,∠P′FC=45°,
∴P′C=FC×=,∴PC的最小值为;
(3)解:如图2,∵DF=FC,OA=OC,∴OF∥AD,
∴∠DFO=180°﹣∠ADF=90°,
∴当点P与点F重合时,∠DPO=90°,此时,AP==2,
当点P在AF上时,作PG⊥AD于G,PH⊥AB于H,
∵AP平分∠DAB,PG⊥AD,PH⊥AB,
∴PG=PH,
设PG=PH=a,
由勾股定理得,DP2=(2﹣a)2+a2,OP2=(2﹣a)2+(1﹣a)2,OD2=5,
当∠DPO=90°时,DP2+OP2=OD2,即(2﹣a)2+a2+(2﹣a)2+(1﹣a)2=5,
解得,a1=2(舍去),a2=,当a=时,AP=,
综上所述,∠DPO=90°时,AP=2或.
每日一题79 参考答案
【解答】证明:(1)连接GC,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,∠ABD=∠CBD=45°,
又∵BG=BG,∴△ABG≌△CBG(SAS),
∴AG=CG,∠BAG=∠BCG,
∵∠ABC+∠BAG+∠AGF+∠BFG=360°,且∠ABC=∠AGF=90°,
∴∠BAG+∠BFG=180°,
∴∠BCG+∠BFG=180°,
∵∠BFG+∠GFC=180°,
∴∠BCG=∠GFC,
∴GC=GF,
∴AG=FG;
(2)如图2,过点G作GH⊥BC于H,
∵AB=10,BF=4,
∴AF2=AB2+BF2=AG2+GF2,
∴GF2=58,
∵∠DBC=45°,GH⊥BC,
∴BH=GH,BG=GH,
∵GF2=GH2+FH2,
∴58=GH2+(GH﹣4)2,
∴GH=7,(负值舍去),
∴BG=7;
(3)如图,在AB上截取BF=BN,连接NF,
∵AG=GF,AG⊥GF,∴∠EAF=45°,
∵AE=AF,AB=AD,∴Rt△ABF≌Rt△ADE(HL),
∴∠BAF=∠DAE=22.5°,BF=DE,∴CF=CE,
∵BF=BN,∠ABC=90°,∴NF=BF,∠BNF=∠BFN=45°,
∴∠BAF=∠AFN=22.5°,∴AN=NF=BF,
∵AB=BC,∴BN+AN=BF+FC,∴FC=BF,∴BC=(+1)BF,
∴正方形ABCD与△CEF的面积之比=BC2:FC2=3+2:1.
每日一题80 参考答案
【解答】证明:(1)∵四边形ABCD为“对垂四边形”,
∴AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AB2+CD2=AD2+BC2;
(2)∵∠BAC=∠BDC,∠AOB=∠COD,
∴∠3=∠ACD,
∵∠3=∠1+∠2,∠ACD=∠ACE+∠2,
∴∠1=∠ACE,
∴∠BOC=∠BEC=90°,
∴AC⊥BD,
∴四边形ABCD为“对垂四边形”;
(3)过点A作AH⊥DC,交CD延长线于点H,
设CD=x,则BC=DC=x,
∵四边形ABCD为“对垂四边形”,AD=3,
∴AB2+CD2=AD2+BC2,
∴AB2=9+5x2﹣x2=9+4x2,
∵AB=AC,
∴AC2=9+4x2,
∵∠ADC=120°,
∴∠ADH=60°,∠DAH=30°,
∴DH=AD=,AH=DH=,
∵AC2=AH2+CH2,
∴9+4x2=+(x+)2,
∴x1=0(舍去),x2=1,
∴CD的长度1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
