浙教版八年级下册数学每日一题81-85(第五章 特殊平行四边形)培优练习(含解析)
文档属性
| 名称 | 浙教版八年级下册数学每日一题81-85(第五章 特殊平行四边形)培优练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 14:46:49 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
每日一题81
班级 姓名 小组
81.如图,在 ABCD中,O是对角线AC的中点,AB⊥AC,BC=4cm,∠B=60°,动点P从点B出发,以2cm/s的速度沿折线BC﹣CD向终点D运动,连接PO并延长交折线DA﹣AB于点Q,设点P的运动时间为t(s).
(1)当PQ与 ABCD的边垂直时,求PQ的长;
(2)当t取何值时,以A,P,C,Q四点组成的四边形是矩形,并说明理由;
(3)当t取何值时,CQ所在直线恰好将 ABCD的面积分成1:3的两部分.
每日一题82
班级 姓名 小组
82.定义:正方形ABCD内部一点P,若∠APB是直角,则称△APB为AB边上的弦图三角形(如图1).
(1)如图2,在正方形ABCD中,点EF分别是AD,CD上两点,AFBE交于点G,若AE=DF,求证:△AGB是AB边上的弦图三角形.
(2)如图3,正方形ABCD中,△AGB是AB边上的弦图三角形,点O为AB中点,若正方形边长为2,
①直接写出OG的长为 ;DG的最小值为 .
②若CG=BC(如图4)求DG的长.
每日一题83
班级 姓名 小组
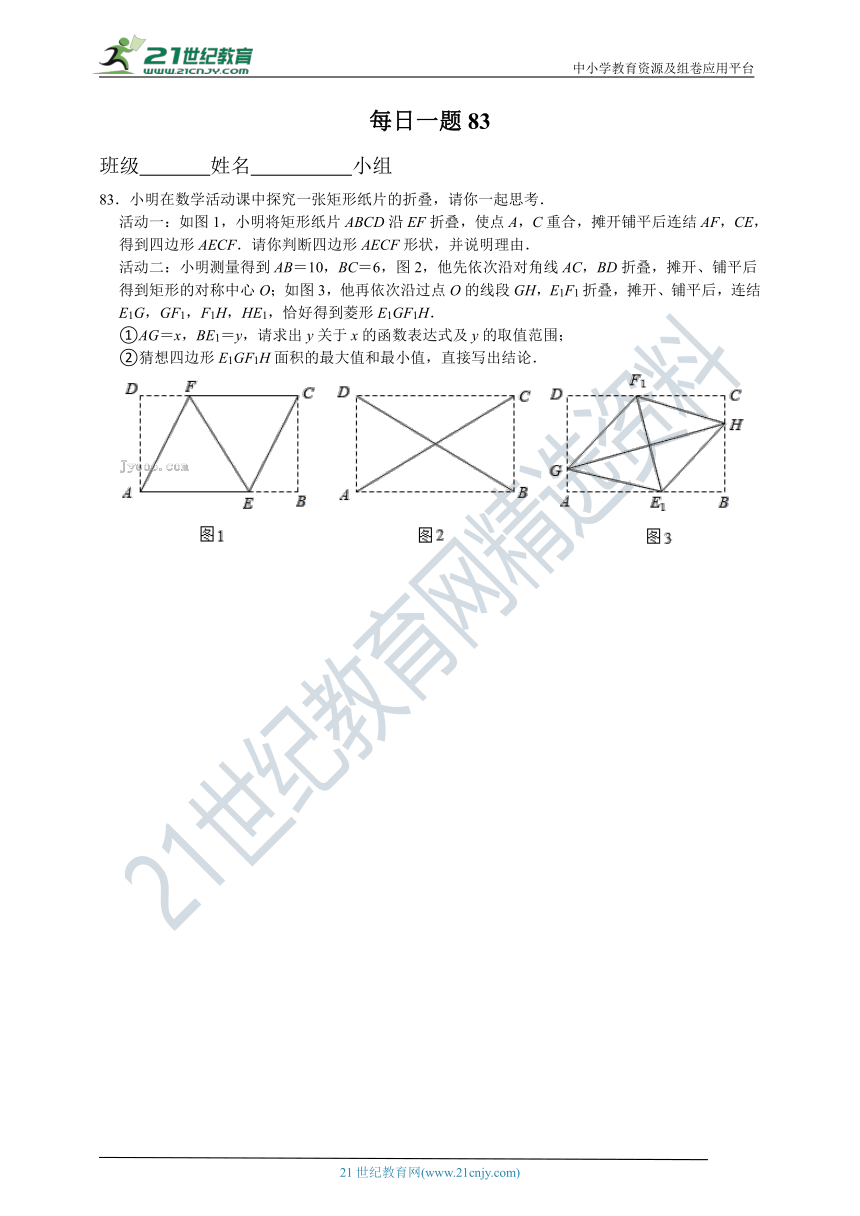
83.小明在数学活动课中探究一张矩形纸片的折叠,请你一起思考.
活动一:如图1,小明将矩形纸片ABCD沿EF折叠,使点A,C重合,摊开铺平后连结AF,CE,得到四边形AECF.请你判断四边形AECF形状,并说明理由.
活动二:小明测量得到AB=10,BC=6,图2,他先依次沿对角线AC,BD折叠,摊开、铺平后得到矩形的对称中心O;如图3,他再依次沿过点O的线段GH,E1F1折叠,摊开、铺平后,连结E1G,GF1,F1H,HE1,恰好得到菱形E1GF1H.
①AG=x,BE1=y,请求出y关于x的函数表达式及y的取值范围;
②猜想四边形E1GF1H面积的最大值和最小值,直接写出结论.
每日一题84
班级 姓名 小组
84.如图,在矩形ABCO中,点O为坐标原点,点A,C分别在x轴、y轴的正半轴上,OA比OC大2,比AC小2.反比例函数y=(k>0,x>0)的图象经过矩形对角线AC,BO的交点D.
(1)求OA的长和此反比例函数的表达式;
(2)若反比例函数y=(m>0,x>0)的图象经过矩形ABCO边BC的中点;
①求m的值.
②在双曲线y=(m>0,x>0)上任取一点G,过点G作GE⊥x轴于点E,交双曲线y=(k>0,x>0)于F点,过点G作GK⊥y轴于点K,交双曲线y=(k>0,x>0)于H点.求△GHF的面积.
每日一题85
班级 姓名 小组
85.(1)如图1,四边形ACDE中,△ABC与△BDE均为直角三角形,且AB⊥BE,∠BEA=45°,求证:△ABC≌△BED.
(2)如图2,点A(1,2),连接OA,将射线OA绕点O按逆时针方向旋转45°.得到射线OB,AC⊥OA交OB于点C,分别过点A,点C作x轴,AD的垂线,垂足分别为D,E,由(1)得 (填写两个三角形全等),所以CE= ,AE= ,C的坐标为 ,则直线OB的解析式为 .
(3)如图3,点A(3,3)在反比例函数y=的图象上,B(0,2)作射线AB,将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象的另一支于点C,求点C的坐标.
每日一题81 参考答案
81.解:(1)当PQ⊥BC时,如图1,
∵AB⊥AC,∴∠BAC=90°,
在Rt△ABC中,BC=4cm,∠B=60°,∴∠ACB=30°,AB=2,AC=2,
∵点O是AC的中点,∴OC=AC=,
在Rt△OPC中,OP=OC=,易知,△AOQ≌△COP,
∴OQ=OP,∴PQ=2OP=cm,
当PQ⊥CD时,∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠ACD=∠BAC=90°,
∴点P与点C重合,点Q和点A重合,∴PQ=AC=2cm,
综上所述,当PQ与 ABCD的边垂直时,PQ=cm或2cm.
(2)当点P在BC边时,如图2,
∵四边形APCQ是矩形,∴∠APC=90°,
在Rt△ABP中,∠B=60°,AB=2cm,∴BP=1cm,
∵动点P从点B出发,以2cm/s的速度沿折线BC﹣CD向终点D运动,∴t=1÷2=秒,
当点P在CD上时,∵四边形AQCP是矩形,∴∠AQC=90°,
∵∠BAC=90°,由过点C垂直于AB的直线有且只有一条,得出此种情况不存在,
即:当t=秒时,以点A,P,C,Q为顶点的四边形知矩形;
(3)∵AC是平行四边形ABCD的对角线,
∴S△ABC=S△ACD=S ABCD,
∵CQ所在直线恰好将 ABCD的面积分成1:3的两部分,
∴当点Q在边AD上时,∴点Q是AD的中点,∴AQ=AD,
易知,△AOQ≌△COP,∴CP=AQ=AD=BC=2,
∴BP=2,∴t=2÷2=1秒,
当点Q在边AB上时,同理:点P是CD的中点,∴t=(4+1)÷2=秒,
即:t为1秒或秒时,CQ将平行四边形ABCD的面积分成1:3两部分.
每日一题82 参考答案
82.(1)证明:如图2,∵四边形ABCD是正方形,∴AB=DA,∠BAE=∠ADF=90°,
∵AE=DF,∴△BAE≌△ADF(SAS),∴∠ABE=∠DAF,
∵∠ABE+∠BAG=∠DAF+∠BAG=∠BAD=90°,
∴∠AGB=180°﹣90°=90°,∴△AGB是AB边上的弦图三角形.
(2)①如图3,连接OD,
∵△AGB是AB边上的弦图三角形,∴∠AGB=90°,
∵O为AB的中点,且AB=2,∴OG=AB=1;
∵∠OAD=90°,OA=AB=1,AD=2,
∴OD2=12+22=5,∴OD=,
∵DG+OG≤OD,∴DG+1≤,
∴当点G在线段OD上时,DG+1的值最小,此时DG的值最小,
由DG+1=得,DG=,故答案为:1;.
②如图4,延长OG交AD于点Q,连接OC、CQ,CQ交DG于点R,
∵OG=AB=OB,CG=BC,OC=OC,
∴△OBC≌△OGC(SSS),∴∠OGC=∠OBC=90°,
∴∠QGC=180°﹣90°=90°,∴∠QGC=∠QDC=90°,
∵CQ=CQ,CG=BC=CD,∴Rt△GCQ≌Rt△DCQ(HL),
∴GQ=DQ,∴CQ垂直平分DG,
∴DR=GR,DR⊥CQ,
设GQ=DQ=m,则AQ=2﹣m,OQ=1+m,
由OA2+AQ2=OQ2,得12+(2﹣m)2=(1+m)2,
解得m=,∴DQ=,
∴CQ2=DQ2+CD2=()2+22=,
∴CQ==,
由CQ DR=CD DQ,得×DR=×2×,解得DR=,
∴DG=2DR=2×=.
每日一题83 参考答案
83.解:活动一:结论:四边形AECF是菱形.
理由:如图1中,
∵四边形ABCD是矩形,∴AB∥CD,∴∠CFE=∠AEF,
由翻折的性质可知,∠CFE=∠AFE,FC=AF,
∴∠AEF=∠AFE,∴AF=AE,∴AE=CF,
∵AE=CF,∴四边形AECF是平行四边形,
∵FC=FA,∴四边形AECF是菱形.
活动二:①如图3中,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,AD=BC=6,AB=CD=10,
根据对称性可知,DF1=BE1=y,AE1=10﹣y,AG=x,DG=6﹣x,
∵GF1=GE1,
∴y2+(6﹣x)2=x2+(10﹣y)2,
整理得,y=x+(0≤x≤6).
当x=0时,y=,
当x=6时,y=,
∴≤y≤.
②当GH⊥AD时,菱形GE1HF1的面积最小,最小值=×10×6=30.
当GH是矩形ABCD的对角线时,菱形GE1HF1的面积最大,最大值=×6=.
每日一题84 参考答案
84.解:(1)设OA=m,则OC=m﹣2,AC=m+2,
∵AC2=OA2+OC2,∴(m+2)2=m2+(m﹣2)2,
解得m1=8,m2=0(舍去),∴OA=8,OC=6,∴A(8,0),C(0,6),
∵矩形对角线AC,BO的交点D,∴D(4,3),
∵反比例函数y=(k>0,x>0)的图象经过点D,∴k=4×3=12,
∴此反比例函数的表达式为y=;
(2)①∵OA=8,OC=6,∴B(8,6),
∴BC的中点为(4,6),AB的中点为(8,3),
∵反比例函数y=(m>0,x>0)的图象经过矩形ABCO边BC的中点,
∴m=4×6=24;
②如图,设G(a,),则F(a,),H(,),
∴S△GFH=GH GF=×(﹣)=3.
每日一题85 参考答案
85.解:(1)∵AB⊥BE,∠AEB=45°,
∴AB=BE,
∵∠BED+∠EBD=90°,∠ABC+∠EBD=90°,
∴∠BED=∠ABC,
在△ABC和△BED中,∠BED=∠ABC,∠EDB=∠ACB,BE=AB,
∴△ABC≌△BDE(AAS);
(2)由(1)同理可得:△AEC≌△ODA(AAS),
∴CE=AD=2,AE=OD=1,C的坐标为(﹣1,3),
设直线OB的解析式为y=kx.
∴﹣k=3,∴k=﹣3,∴直线OB的解析式为y=﹣3x;
故答案为:△AEC≌△ODA;2(或AD);1(或OD);(﹣1,3);y=﹣3x;
(3)如图,过B作BF⊥AC于点F,过F作FD⊥y轴于点D,过A作AE⊥DF于点E,
则△ABF为等腰直角三角形,
根据(1)同理可得△AEF≌△FDB,设BD=a,则EF=a,
∵点A(3,3)和点B(0,2),∴DF=3﹣a=AE,OD=OB﹣BD=2﹣a,
∵AE+OD=3,∴3﹣a+2﹣a=3,解得a=1,
则OD=2﹣1=1,DF=3﹣a=3﹣1=2,∴F(2,1),
设直线AF的解析式为y=kx+b,则,解得,∴y=2x﹣3①,
把点A点坐标代入y=中,,解得:k=9,故反比例函数的表达式为:y=②,
联立①②并解得:(不符合题意,舍去)或,
∴C(﹣,﹣6),
故点C的坐标为:(﹣,﹣6).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题81
班级 姓名 小组
81.如图,在 ABCD中,O是对角线AC的中点,AB⊥AC,BC=4cm,∠B=60°,动点P从点B出发,以2cm/s的速度沿折线BC﹣CD向终点D运动,连接PO并延长交折线DA﹣AB于点Q,设点P的运动时间为t(s).
(1)当PQ与 ABCD的边垂直时,求PQ的长;
(2)当t取何值时,以A,P,C,Q四点组成的四边形是矩形,并说明理由;
(3)当t取何值时,CQ所在直线恰好将 ABCD的面积分成1:3的两部分.
每日一题82
班级 姓名 小组
82.定义:正方形ABCD内部一点P,若∠APB是直角,则称△APB为AB边上的弦图三角形(如图1).
(1)如图2,在正方形ABCD中,点EF分别是AD,CD上两点,AFBE交于点G,若AE=DF,求证:△AGB是AB边上的弦图三角形.
(2)如图3,正方形ABCD中,△AGB是AB边上的弦图三角形,点O为AB中点,若正方形边长为2,
①直接写出OG的长为 ;DG的最小值为 .
②若CG=BC(如图4)求DG的长.
每日一题83
班级 姓名 小组
83.小明在数学活动课中探究一张矩形纸片的折叠,请你一起思考.
活动一:如图1,小明将矩形纸片ABCD沿EF折叠,使点A,C重合,摊开铺平后连结AF,CE,得到四边形AECF.请你判断四边形AECF形状,并说明理由.
活动二:小明测量得到AB=10,BC=6,图2,他先依次沿对角线AC,BD折叠,摊开、铺平后得到矩形的对称中心O;如图3,他再依次沿过点O的线段GH,E1F1折叠,摊开、铺平后,连结E1G,GF1,F1H,HE1,恰好得到菱形E1GF1H.
①AG=x,BE1=y,请求出y关于x的函数表达式及y的取值范围;
②猜想四边形E1GF1H面积的最大值和最小值,直接写出结论.
每日一题84
班级 姓名 小组
84.如图,在矩形ABCO中,点O为坐标原点,点A,C分别在x轴、y轴的正半轴上,OA比OC大2,比AC小2.反比例函数y=(k>0,x>0)的图象经过矩形对角线AC,BO的交点D.
(1)求OA的长和此反比例函数的表达式;
(2)若反比例函数y=(m>0,x>0)的图象经过矩形ABCO边BC的中点;
①求m的值.
②在双曲线y=(m>0,x>0)上任取一点G,过点G作GE⊥x轴于点E,交双曲线y=(k>0,x>0)于F点,过点G作GK⊥y轴于点K,交双曲线y=(k>0,x>0)于H点.求△GHF的面积.
每日一题85
班级 姓名 小组
85.(1)如图1,四边形ACDE中,△ABC与△BDE均为直角三角形,且AB⊥BE,∠BEA=45°,求证:△ABC≌△BED.
(2)如图2,点A(1,2),连接OA,将射线OA绕点O按逆时针方向旋转45°.得到射线OB,AC⊥OA交OB于点C,分别过点A,点C作x轴,AD的垂线,垂足分别为D,E,由(1)得 (填写两个三角形全等),所以CE= ,AE= ,C的坐标为 ,则直线OB的解析式为 .
(3)如图3,点A(3,3)在反比例函数y=的图象上,B(0,2)作射线AB,将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象的另一支于点C,求点C的坐标.
每日一题81 参考答案
81.解:(1)当PQ⊥BC时,如图1,
∵AB⊥AC,∴∠BAC=90°,
在Rt△ABC中,BC=4cm,∠B=60°,∴∠ACB=30°,AB=2,AC=2,
∵点O是AC的中点,∴OC=AC=,
在Rt△OPC中,OP=OC=,易知,△AOQ≌△COP,
∴OQ=OP,∴PQ=2OP=cm,
当PQ⊥CD时,∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠ACD=∠BAC=90°,
∴点P与点C重合,点Q和点A重合,∴PQ=AC=2cm,
综上所述,当PQ与 ABCD的边垂直时,PQ=cm或2cm.
(2)当点P在BC边时,如图2,
∵四边形APCQ是矩形,∴∠APC=90°,
在Rt△ABP中,∠B=60°,AB=2cm,∴BP=1cm,
∵动点P从点B出发,以2cm/s的速度沿折线BC﹣CD向终点D运动,∴t=1÷2=秒,
当点P在CD上时,∵四边形AQCP是矩形,∴∠AQC=90°,
∵∠BAC=90°,由过点C垂直于AB的直线有且只有一条,得出此种情况不存在,
即:当t=秒时,以点A,P,C,Q为顶点的四边形知矩形;
(3)∵AC是平行四边形ABCD的对角线,
∴S△ABC=S△ACD=S ABCD,
∵CQ所在直线恰好将 ABCD的面积分成1:3的两部分,
∴当点Q在边AD上时,∴点Q是AD的中点,∴AQ=AD,
易知,△AOQ≌△COP,∴CP=AQ=AD=BC=2,
∴BP=2,∴t=2÷2=1秒,
当点Q在边AB上时,同理:点P是CD的中点,∴t=(4+1)÷2=秒,
即:t为1秒或秒时,CQ将平行四边形ABCD的面积分成1:3两部分.
每日一题82 参考答案
82.(1)证明:如图2,∵四边形ABCD是正方形,∴AB=DA,∠BAE=∠ADF=90°,
∵AE=DF,∴△BAE≌△ADF(SAS),∴∠ABE=∠DAF,
∵∠ABE+∠BAG=∠DAF+∠BAG=∠BAD=90°,
∴∠AGB=180°﹣90°=90°,∴△AGB是AB边上的弦图三角形.
(2)①如图3,连接OD,
∵△AGB是AB边上的弦图三角形,∴∠AGB=90°,
∵O为AB的中点,且AB=2,∴OG=AB=1;
∵∠OAD=90°,OA=AB=1,AD=2,
∴OD2=12+22=5,∴OD=,
∵DG+OG≤OD,∴DG+1≤,
∴当点G在线段OD上时,DG+1的值最小,此时DG的值最小,
由DG+1=得,DG=,故答案为:1;.
②如图4,延长OG交AD于点Q,连接OC、CQ,CQ交DG于点R,
∵OG=AB=OB,CG=BC,OC=OC,
∴△OBC≌△OGC(SSS),∴∠OGC=∠OBC=90°,
∴∠QGC=180°﹣90°=90°,∴∠QGC=∠QDC=90°,
∵CQ=CQ,CG=BC=CD,∴Rt△GCQ≌Rt△DCQ(HL),
∴GQ=DQ,∴CQ垂直平分DG,
∴DR=GR,DR⊥CQ,
设GQ=DQ=m,则AQ=2﹣m,OQ=1+m,
由OA2+AQ2=OQ2,得12+(2﹣m)2=(1+m)2,
解得m=,∴DQ=,
∴CQ2=DQ2+CD2=()2+22=,
∴CQ==,
由CQ DR=CD DQ,得×DR=×2×,解得DR=,
∴DG=2DR=2×=.
每日一题83 参考答案
83.解:活动一:结论:四边形AECF是菱形.
理由:如图1中,
∵四边形ABCD是矩形,∴AB∥CD,∴∠CFE=∠AEF,
由翻折的性质可知,∠CFE=∠AFE,FC=AF,
∴∠AEF=∠AFE,∴AF=AE,∴AE=CF,
∵AE=CF,∴四边形AECF是平行四边形,
∵FC=FA,∴四边形AECF是菱形.
活动二:①如图3中,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,AD=BC=6,AB=CD=10,
根据对称性可知,DF1=BE1=y,AE1=10﹣y,AG=x,DG=6﹣x,
∵GF1=GE1,
∴y2+(6﹣x)2=x2+(10﹣y)2,
整理得,y=x+(0≤x≤6).
当x=0时,y=,
当x=6时,y=,
∴≤y≤.
②当GH⊥AD时,菱形GE1HF1的面积最小,最小值=×10×6=30.
当GH是矩形ABCD的对角线时,菱形GE1HF1的面积最大,最大值=×6=.
每日一题84 参考答案
84.解:(1)设OA=m,则OC=m﹣2,AC=m+2,
∵AC2=OA2+OC2,∴(m+2)2=m2+(m﹣2)2,
解得m1=8,m2=0(舍去),∴OA=8,OC=6,∴A(8,0),C(0,6),
∵矩形对角线AC,BO的交点D,∴D(4,3),
∵反比例函数y=(k>0,x>0)的图象经过点D,∴k=4×3=12,
∴此反比例函数的表达式为y=;
(2)①∵OA=8,OC=6,∴B(8,6),
∴BC的中点为(4,6),AB的中点为(8,3),
∵反比例函数y=(m>0,x>0)的图象经过矩形ABCO边BC的中点,
∴m=4×6=24;
②如图,设G(a,),则F(a,),H(,),
∴S△GFH=GH GF=×(﹣)=3.
每日一题85 参考答案
85.解:(1)∵AB⊥BE,∠AEB=45°,
∴AB=BE,
∵∠BED+∠EBD=90°,∠ABC+∠EBD=90°,
∴∠BED=∠ABC,
在△ABC和△BED中,∠BED=∠ABC,∠EDB=∠ACB,BE=AB,
∴△ABC≌△BDE(AAS);
(2)由(1)同理可得:△AEC≌△ODA(AAS),
∴CE=AD=2,AE=OD=1,C的坐标为(﹣1,3),
设直线OB的解析式为y=kx.
∴﹣k=3,∴k=﹣3,∴直线OB的解析式为y=﹣3x;
故答案为:△AEC≌△ODA;2(或AD);1(或OD);(﹣1,3);y=﹣3x;
(3)如图,过B作BF⊥AC于点F,过F作FD⊥y轴于点D,过A作AE⊥DF于点E,
则△ABF为等腰直角三角形,
根据(1)同理可得△AEF≌△FDB,设BD=a,则EF=a,
∵点A(3,3)和点B(0,2),∴DF=3﹣a=AE,OD=OB﹣BD=2﹣a,
∵AE+OD=3,∴3﹣a+2﹣a=3,解得a=1,
则OD=2﹣1=1,DF=3﹣a=3﹣1=2,∴F(2,1),
设直线AF的解析式为y=kx+b,则,解得,∴y=2x﹣3①,
把点A点坐标代入y=中,,解得:k=9,故反比例函数的表达式为:y=②,
联立①②并解得:(不符合题意,舍去)或,
∴C(﹣,﹣6),
故点C的坐标为:(﹣,﹣6).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
