浙教版八年级下册数学每日一题86-90(第六章 反比例函数)培优练习(含解析)
文档属性
| 名称 | 浙教版八年级下册数学每日一题86-90(第六章 反比例函数)培优练习(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
每日一题86
班级 姓名 小组
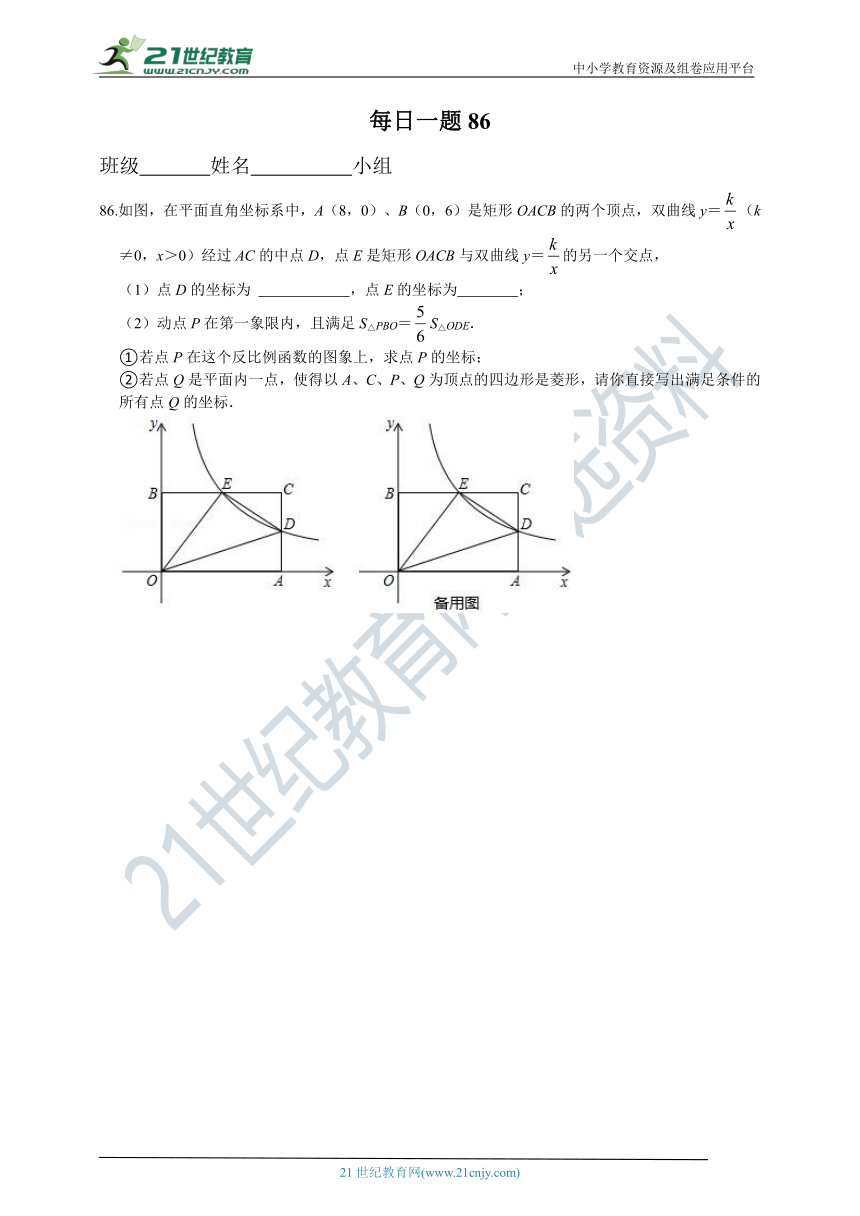
86.如图,在平面直角坐标系中,A(8,0)、B(0,6)是矩形OACB的两个顶点,双曲线y=(k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线y=的另一个交点,
(1)点D的坐标为 ,点E的坐标为 ;
(2)动点P在第一象限内,且满足S△PBO=S△ODE.
①若点P在这个反比例函数的图象上,求点P的坐标;
②若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
每日一题87
班级 姓名 小组
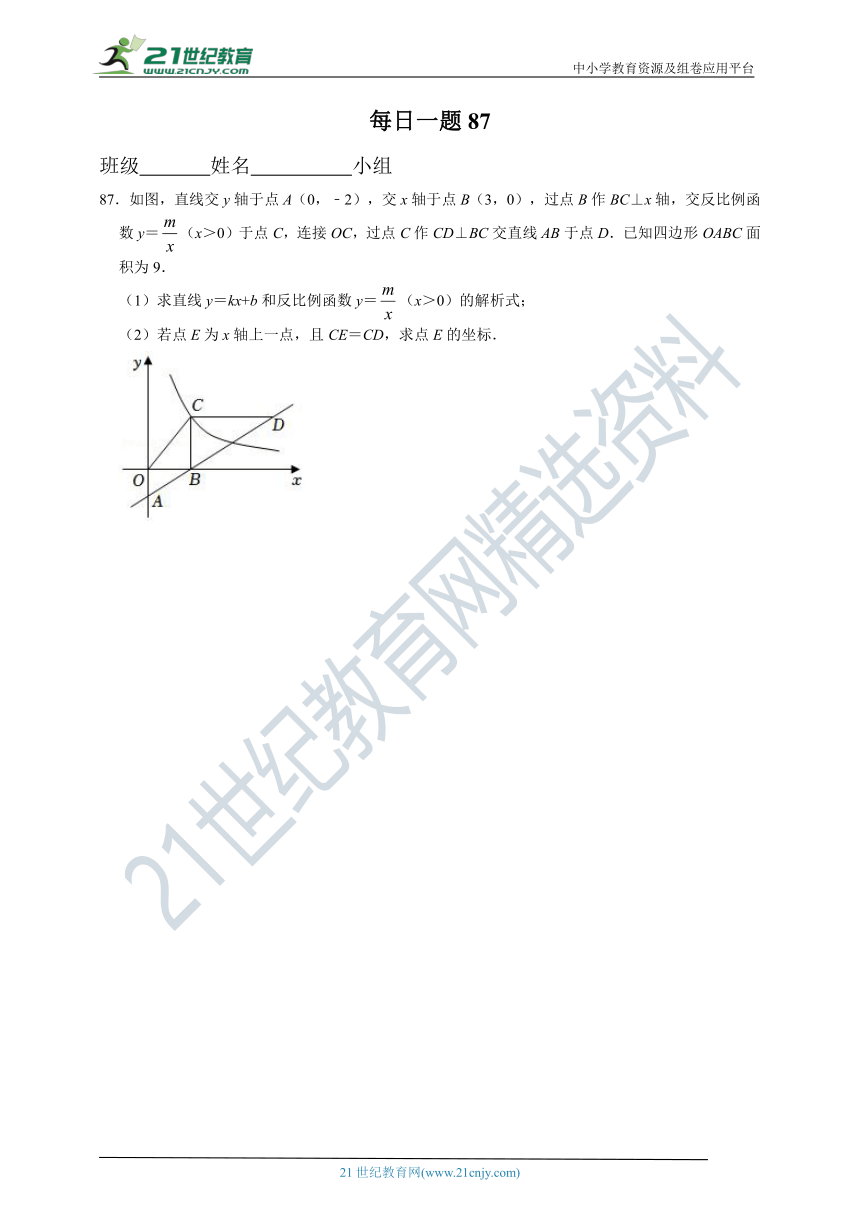
87.如图,直线交y轴于点A(0,﹣2),交x轴于点B(3,0),过点B作BC⊥x轴,交反比例函数y=(x>0)于点C,连接OC,过点C作CD⊥BC交直线AB于点D.已知四边形OABC面积为9.
(1)求直线y=kx+b和反比例函数y=(x>0)的解析式;
(2)若点E为x轴上一点,且CE=CD,求点E的坐标.
每日一题88
班级 姓名 小组
88.如图,一次函数y1=mx+n(m≠0)的图象与反比例函数的图象交于A(a,﹣1),B(﹣1,3)两点,且一次函数y1的图象交x轴于点C,交y轴于点D.
(1)求一次函数和反比例函数的解析式;
(2)在第四象限的反比例图象上有一点P,使得S△OCP=6S△OBD,请求出点P的坐标;
(3)对于反比例函数,当y≤3时,直接写出x的取值范围.
每日一题89
班级 姓名 小组
89.如图,已知一次函数y=k1x+b与反比例函数y=的图象交于第一象限内的点A(1,6)和B(6,m),与x轴交于点C.
(1)分别求出这两个函数的表达式;
(2)①观察图象,直接写出不等式k1x+b≥的解集;②请连接OA、OB,并计算△AOB的面积;
(3)是否存在坐标平面内的点P,使得由点O,A,C,P组成的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
每日一题90
班级 姓名 小组
90.如图,反比例函数的图象与过点A(0,﹣1),B(4,1)的直线交于点B和C.
(1)求直线AB和反比例函数的解析式;
(2)已知点D(﹣1,0),直线CD与反比例函数图象在第一象限的交点为E,直接写出点E的坐标,并求△BCE的面积.
每日一题86 参考答案
【解答】解:(1)∵四边形OACB是矩形,
∴AC=OB=6,∴C(8,6),
∵点D是AC的中点,∴D(8,3),∴k=8×3=24,∴y=,
当y=6时,x=4,∴E(4,6),
故答案为:(8,3),(4,6);
(2)①由题意知,S△ODE=S梯形OACE﹣S△OAD﹣S△ECD
=﹣﹣=18,
∵S△PBO=S△ODE.∴×6×xP=×18,∴xP=5,∴y=,
∴P的坐标为(5,);
②由①知,点P在直线x=5上,设直线x=5交x轴于H,
当AC=AP=6时,若点P在第一象限,
∴PH==3,
∴Q(5,3+6),
当点P在第四象限舍去,
当CA=CP时,
同理得,Q(5,﹣3),Q'(5,3),
当PC=PA时,点P(5,3),
则点Q与P关于AC对称,
∴Q(11,3),
综上,点Q(5,3+6)或(5,﹣3)或(5,3)或(11,3).
每日一题87 参考答案
解:(1)∵直线y=kx+b交y轴于点A(0,﹣2),交x轴于点B(3,0),
∴,解得,∴直线的解析式为y=x﹣2;
∵点A(0,﹣2),点B(3,0),∴OA=2,OB=3,
∴S△AOB===3,
∵四边形OABC面积为9,
∴S△COB=9﹣3=6,
∵BC⊥x轴,点C反比例函数y=(x>0)图象上,
∴S△COB=|m|=6,
∵在第一象限,
∴m=12,
∴反比例函数的解析式为y=(x>0);
(2)把x=3代入y=(x>0)得,y=4,
∴C(3,4),
∵CD⊥BC交直线AB于点D,
∴D的纵坐标为4,
把y=4代入y=x﹣2得,4=x﹣2,解得x=9,
∴D(9,4),
∴CD=9﹣3=6,
设E的坐标为(x,0),
∵CE=CD,
∴(3﹣x)2+42=36,
解得x=3+2或x=3﹣2,
∴E的坐标为(3+2,0)或(3﹣2,0).
每日一题88参考答案
解:(1)∵比例函数的图象过点B(﹣1,3),
∴k=﹣1×3=﹣3,
∴y2=﹣,
∵A(a,﹣1)在双曲线上.
∴﹣1=﹣,
∴a=3,
∴A(3,﹣1),
∵直线y1=kx+b经过A、B两点,
∴,解得,
∴一次函数的解析式y1=﹣x+2;
(2)在y=﹣x+2中,当x=0时,y=2;当y=0时,则x=2,
∴D(0,2),C(2,0),
∴OD=OC=2,
∴S△OBD==1,
∵S△OCP=6S△OBD,
∴S△OCP=OC |yP|=6,即|yP|=6,
∴yp=﹣6,
代入y2=﹣得,﹣6=﹣,解得x=,
∴P的坐标为(,﹣6);
(3)观察图象可知,对于反比例函数,当y≤3时,x的取值范围是x≤﹣1或x>0.
每日一题89 参考答案
解:(1)∵点A(1,6)在反比例函数y=的图象上,∴6=,
解得:k2=6,∴反比例函数的表达式是:y=;
∵B(6,m)在反比例函数y=的图象上,∴m==1,∴B(6,1),
将点A(1,6),B(6,1)代入y=k1x+b,可得:
,解得:,∴一次函数表达式是:y=﹣x+7;
(2)①∵点A(1,6),B(6,1),
∴不等式k1x+b≥的解集是:x<0或1≤x≤6;
②
记直线AB交y轴于D,由(1)知,直线AB的解析式为y=﹣x+7,
则D(0,7),C(7,0),
∴S△AOB=S△AOC﹣S△BOC)=×6×7﹣×7×1=;
(3)如图所示:当AP∥OC且AP=OC时,则AP=OC=7,
∵A(1,6),∴P点坐标为:(8,6);
当AP′∥OC且AP′=OC时,则AP′=OC=7,
∵A(1,6),∴P′点坐标为:(﹣6,6);
当AO∥P″C,且AO=P″C时,
则点A与P″到x轴距离相等,且P″点横坐标为7﹣1=6,
∴P″点坐标为:(6,﹣6);
综上所述:点P的坐标为:(8,6),(﹣6,6),(6,﹣6).
每日一题90 参考答案
90.解:(1)设反比例函数解析式为y,直线AB解析式为y=ax+b,
∵反比例函数的图象过点B(4,1),∴k=4×1=4,
把点A(0,﹣1),B(4,1)代入y=ax+b得
,解得,
∴直线AB为y,反比例函数的解析式为y;
(2)解得或,
∴C(﹣2,﹣2),
设直线CD为y=mx+n,
把C(﹣2,﹣2),D(﹣1,0)代入得
,解得,
∴直线CD为y=2x+2,
由得或,
∴E(1,4),
∴S△BCE=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题86
班级 姓名 小组
86.如图,在平面直角坐标系中,A(8,0)、B(0,6)是矩形OACB的两个顶点,双曲线y=(k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线y=的另一个交点,
(1)点D的坐标为 ,点E的坐标为 ;
(2)动点P在第一象限内,且满足S△PBO=S△ODE.
①若点P在这个反比例函数的图象上,求点P的坐标;
②若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
每日一题87
班级 姓名 小组
87.如图,直线交y轴于点A(0,﹣2),交x轴于点B(3,0),过点B作BC⊥x轴,交反比例函数y=(x>0)于点C,连接OC,过点C作CD⊥BC交直线AB于点D.已知四边形OABC面积为9.
(1)求直线y=kx+b和反比例函数y=(x>0)的解析式;
(2)若点E为x轴上一点,且CE=CD,求点E的坐标.
每日一题88
班级 姓名 小组
88.如图,一次函数y1=mx+n(m≠0)的图象与反比例函数的图象交于A(a,﹣1),B(﹣1,3)两点,且一次函数y1的图象交x轴于点C,交y轴于点D.
(1)求一次函数和反比例函数的解析式;
(2)在第四象限的反比例图象上有一点P,使得S△OCP=6S△OBD,请求出点P的坐标;
(3)对于反比例函数,当y≤3时,直接写出x的取值范围.
每日一题89
班级 姓名 小组
89.如图,已知一次函数y=k1x+b与反比例函数y=的图象交于第一象限内的点A(1,6)和B(6,m),与x轴交于点C.
(1)分别求出这两个函数的表达式;
(2)①观察图象,直接写出不等式k1x+b≥的解集;②请连接OA、OB,并计算△AOB的面积;
(3)是否存在坐标平面内的点P,使得由点O,A,C,P组成的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
每日一题90
班级 姓名 小组
90.如图,反比例函数的图象与过点A(0,﹣1),B(4,1)的直线交于点B和C.
(1)求直线AB和反比例函数的解析式;
(2)已知点D(﹣1,0),直线CD与反比例函数图象在第一象限的交点为E,直接写出点E的坐标,并求△BCE的面积.
每日一题86 参考答案
【解答】解:(1)∵四边形OACB是矩形,
∴AC=OB=6,∴C(8,6),
∵点D是AC的中点,∴D(8,3),∴k=8×3=24,∴y=,
当y=6时,x=4,∴E(4,6),
故答案为:(8,3),(4,6);
(2)①由题意知,S△ODE=S梯形OACE﹣S△OAD﹣S△ECD
=﹣﹣=18,
∵S△PBO=S△ODE.∴×6×xP=×18,∴xP=5,∴y=,
∴P的坐标为(5,);
②由①知,点P在直线x=5上,设直线x=5交x轴于H,
当AC=AP=6时,若点P在第一象限,
∴PH==3,
∴Q(5,3+6),
当点P在第四象限舍去,
当CA=CP时,
同理得,Q(5,﹣3),Q'(5,3),
当PC=PA时,点P(5,3),
则点Q与P关于AC对称,
∴Q(11,3),
综上,点Q(5,3+6)或(5,﹣3)或(5,3)或(11,3).
每日一题87 参考答案
解:(1)∵直线y=kx+b交y轴于点A(0,﹣2),交x轴于点B(3,0),
∴,解得,∴直线的解析式为y=x﹣2;
∵点A(0,﹣2),点B(3,0),∴OA=2,OB=3,
∴S△AOB===3,
∵四边形OABC面积为9,
∴S△COB=9﹣3=6,
∵BC⊥x轴,点C反比例函数y=(x>0)图象上,
∴S△COB=|m|=6,
∵在第一象限,
∴m=12,
∴反比例函数的解析式为y=(x>0);
(2)把x=3代入y=(x>0)得,y=4,
∴C(3,4),
∵CD⊥BC交直线AB于点D,
∴D的纵坐标为4,
把y=4代入y=x﹣2得,4=x﹣2,解得x=9,
∴D(9,4),
∴CD=9﹣3=6,
设E的坐标为(x,0),
∵CE=CD,
∴(3﹣x)2+42=36,
解得x=3+2或x=3﹣2,
∴E的坐标为(3+2,0)或(3﹣2,0).
每日一题88参考答案
解:(1)∵比例函数的图象过点B(﹣1,3),
∴k=﹣1×3=﹣3,
∴y2=﹣,
∵A(a,﹣1)在双曲线上.
∴﹣1=﹣,
∴a=3,
∴A(3,﹣1),
∵直线y1=kx+b经过A、B两点,
∴,解得,
∴一次函数的解析式y1=﹣x+2;
(2)在y=﹣x+2中,当x=0时,y=2;当y=0时,则x=2,
∴D(0,2),C(2,0),
∴OD=OC=2,
∴S△OBD==1,
∵S△OCP=6S△OBD,
∴S△OCP=OC |yP|=6,即|yP|=6,
∴yp=﹣6,
代入y2=﹣得,﹣6=﹣,解得x=,
∴P的坐标为(,﹣6);
(3)观察图象可知,对于反比例函数,当y≤3时,x的取值范围是x≤﹣1或x>0.
每日一题89 参考答案
解:(1)∵点A(1,6)在反比例函数y=的图象上,∴6=,
解得:k2=6,∴反比例函数的表达式是:y=;
∵B(6,m)在反比例函数y=的图象上,∴m==1,∴B(6,1),
将点A(1,6),B(6,1)代入y=k1x+b,可得:
,解得:,∴一次函数表达式是:y=﹣x+7;
(2)①∵点A(1,6),B(6,1),
∴不等式k1x+b≥的解集是:x<0或1≤x≤6;
②
记直线AB交y轴于D,由(1)知,直线AB的解析式为y=﹣x+7,
则D(0,7),C(7,0),
∴S△AOB=S△AOC﹣S△BOC)=×6×7﹣×7×1=;
(3)如图所示:当AP∥OC且AP=OC时,则AP=OC=7,
∵A(1,6),∴P点坐标为:(8,6);
当AP′∥OC且AP′=OC时,则AP′=OC=7,
∵A(1,6),∴P′点坐标为:(﹣6,6);
当AO∥P″C,且AO=P″C时,
则点A与P″到x轴距离相等,且P″点横坐标为7﹣1=6,
∴P″点坐标为:(6,﹣6);
综上所述:点P的坐标为:(8,6),(﹣6,6),(6,﹣6).
每日一题90 参考答案
90.解:(1)设反比例函数解析式为y,直线AB解析式为y=ax+b,
∵反比例函数的图象过点B(4,1),∴k=4×1=4,
把点A(0,﹣1),B(4,1)代入y=ax+b得
,解得,
∴直线AB为y,反比例函数的解析式为y;
(2)解得或,
∴C(﹣2,﹣2),
设直线CD为y=mx+n,
把C(﹣2,﹣2),D(﹣1,0)代入得
,解得,
∴直线CD为y=2x+2,
由得或,
∴E(1,4),
∴S△BCE=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
