浙教版八年级下册数学每日一题91-95(第6章 反比例函数)培优练习(含解析)
文档属性
| 名称 | 浙教版八年级下册数学每日一题91-95(第6章 反比例函数)培优练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 14:14:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
每日一题91
班级 姓名 小组
91.如图,一次函数y1=kx+b(k≠0)与反比例函数y2(m≠0)的图象交于
点A(1,2)和B(﹣2,a),与y轴交于点M.
(1)求一次函数和反比例函数的解析式;
(2)在y轴上取一点N,当△AMN的面积为3时,求点N的坐标;
(3)将直线y1向下平移2个单位后得到直线y3,当函数值y1>y2>y3时,求x的取值范围.
每日一题92
班级 姓名 小组
92.如图,在平面直角坐标系xOy中,一次函数yx的图象与反比例函数y(x>0)的图象相交于点A(a,3),与x轴相交于点B.
(1)求反比例函数的表达式;
(2)过点A的直线交反比例函数的图象于另一点C,交x轴正半轴于点D,当△ABD是以BD为底的等腰三角形时,求直线AD的函数表达式及点C的坐标.
每日一题93
班级 姓名 小组
93.如图,直线y=kx+2与双曲线y相交于点A、B,已知点A的横坐标为1.
(1)求直线y=kx+2的解析式及点B的坐标;
(2)以线段AB为斜边在直线AB的上方作等腰直角三角形ABC.求经过点C的双曲线的解析式.
每日一题94
班级 姓名 小组
94.如图,过C点的直线与x轴,y轴分别交于点A,B两点,且BC=AB,过点C作CH⊥x轴,垂足为点H,交反比例函数(x>0)的图象于点D,连接OD,△ODH的面积为6.
(1)求k值和点D的坐标;
(2)如图,连接BD,OC,点E在直线上,且位于第二象限内,若△BDE的面积是△OCD面积的2倍,求点E的坐标.
每日一题95
班级 姓名 小组
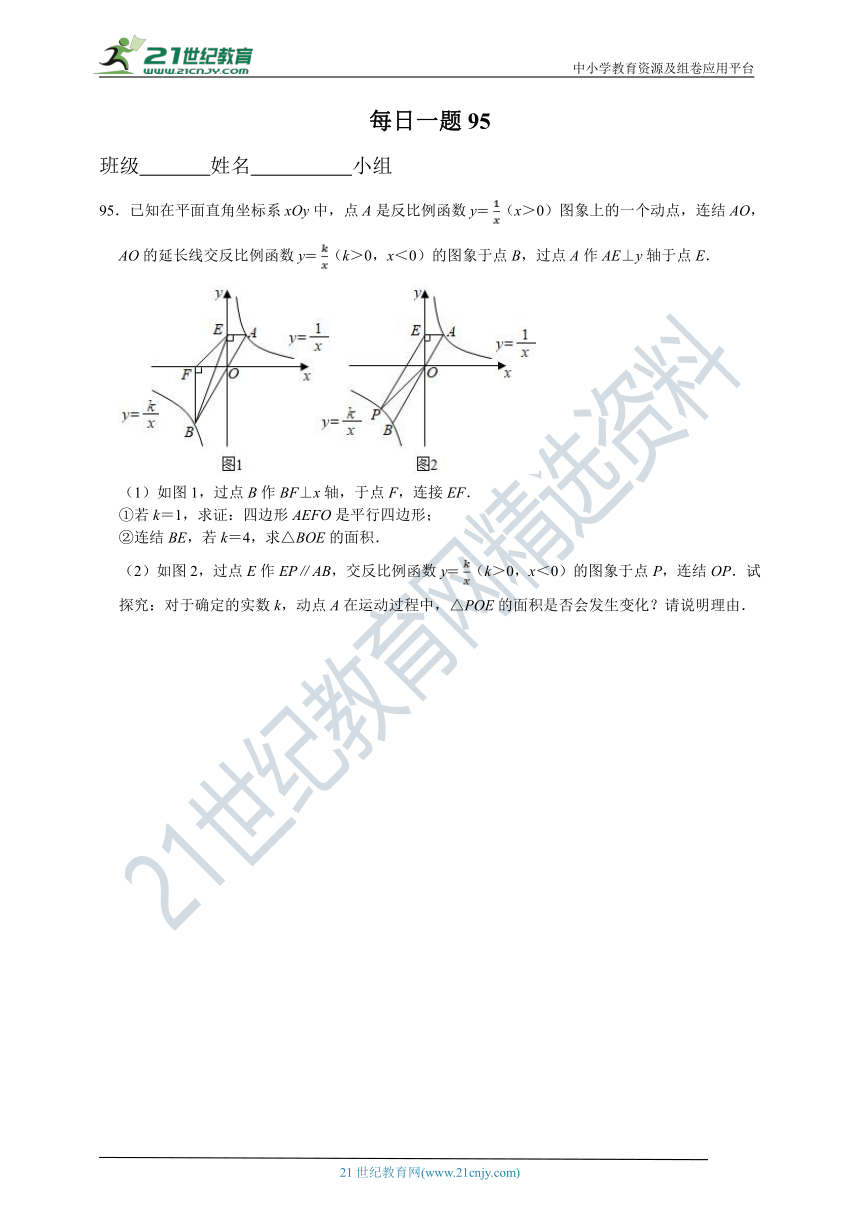
95.已知在平面直角坐标系xOy中,点A是反比例函数y(x>0)图象上的一个动点,连结AO,AO的延长线交反比例函数y(k>0,x<0)的图象于点B,过点A作AE⊥y轴于点E.
(1)如图1,过点B作BF⊥x轴,于点F,连接EF.
①若k=1,求证:四边形AEFO是平行四边形;
②连结BE,若k=4,求△BOE的面积.
(2)如图2,过点E作EP∥AB,交反比例函数y(k>0,x<0)的图象于点P,连结OP.试探究:对于确定的实数k,动点A在运动过程中,△POE的面积是否会发生变化?请说明理由.
每日一题91 参考答案
91.解:(1)∵过点A(1,2),∴ m=1×2=2,∴反比例函数.
当x=﹣2时,a=﹣1,即B(﹣2,﹣1).
∵y1=kx+b过A(1,2)和B(﹣2,﹣1),则,解得,∴y1=x+1.
(2)当x=0时,代入y=x+1中得,y=1,即M(0,1),
∵S△AMNMN |xA|=3且xA=1,∴MN=6,∴N(0,7)或(0,﹣5).
(3)如图,设y2与y3的图像交于C,D两点,
∵y1向下平移两个单位得y3且y1=x+1,∴y3=x﹣1,
联立,解得或,∴C(﹣1,﹣2),D(2,1).
∵y1>y2>y3,∴﹣2<x<﹣1或1<x<2.
每日一题92 参考答案
92.解:(1)∵一次函数yx的图象经过点A(a,3),
∴a3,解得a=2,∴A(2,3),
将A(2,3)代入y(x>0),得:3,
∴k=6,∴反比例函数的表达式为y.
(2)如图,过点A作AE⊥x轴于点E,
在yx中,令y=0,得:x0,
解得x=﹣2,∴B(﹣2,0),
∵E(2,0),∴BE=2﹣(﹣2)=4,
∵△ABD是以BD为底边的等腰三角形,
∴AB=AD,
∵AE⊥BD,∴DE=BE=4,∴D(6,0),
设直线AD的函数表达式为y=mx+n,
∵A(2,3),D(6,0),
∴,解得,
∴直线AD的函数表达式为yx,
联立方程组:,解得(舍去),,
∴点C的坐标为(4,).
每日一题93 参考答案
解:(1)∵点A在双曲线y上,且点A的横坐标为1,
∴点A的纵坐标为,∴点A(1,),
∵点A(1,)在直线y=kx+2上,∴k+2,∴,
∴直线AB的解析式为yx+2.
联立直线AB和双曲线的解析式得,,
解得,(点A的纵横坐标)或, ∴B(3,).
(2)如图,过点A作x轴的垂线,过点B作y轴的垂线,两线相交于点F,过点C作CD⊥AF,交AF于D,过点C作CE⊥BF于E,
∴∠D=∠F=∠CEF=∠CEB=90°,∴四边形CDFE是矩形,∴∠DCE=90°,
∵∠ACB=90°,∴∠ACD=∠BCE,
∵以线段AB为斜边在直线AB的上方作等腰直角三角形ABC,
∴AC=BC,∴△ACD≌△BCE(AAS),∴AD=BE,CD=CE,
设点C(m,n),∵A(1,),B(3,),
∴AD=n,CD=m﹣1,BE=3﹣m,CE=n,
∴,∴,∴C(,2),
设过点C的双曲线的解析式为y,∴k'=25,
∴过点C的双曲线的解析式为y.
每日一题94 参考答案
解:(1)设点D坐标为(m,n),由题意得,∴mn=12.
∵点D在的图象上,∴k=mn=12.
∵直线的图象与x轴交于点A,∴点A的坐标为(-4,0).
∵CH⊥x轴,∴CH∥y轴,∴,
∴OH=AO=4,∴点D的横坐标为4,
∵点D在反比例函数的图象上,∴点D坐标为(4,3).
(2)由(1)知CD∥y轴,.
.
过点E作EFCD,垂足为点 F,交y轴于点M,
.∴点 E 的横坐标为-8.
∵点E 在直线上,∴点E的坐标为(-8,2).
每日一题95 参考答案
解:(1)①证明:设点A的坐标为(a,),则当点k=1时,点B的坐标为(﹣a,),
∴AE=OF=a,∵AE⊥y轴,∴AE∥OF,∴四边形AEFO是平行四边形;
②过点B作BD⊥y轴于点D,如图1,
∵AE⊥y轴,∴AE∥BD,∴△AEO∽△BDO,∴,
∴当k=4时,,即,∴S△BOE=2S△AOE=1;
(2)不改变.理由如下:过点P作PH⊥x轴于点H,PE与x轴交于点G,
设点A的坐标为(a,),点P的坐标为(b,),则AE=a,OE,PH,
∵四边形AEGO是平行四边形,∴∠EAO=∠EGO,AE=OG,
∵∠EGO=∠PGH,∴∠EAO=∠PGH,
又∵∠PHG=∠AEO,∴△AEO∽△GHP,∴,
∵GH=OH﹣OG=﹣b﹣a,∴,∴k=0,解得,
∵a,b异号,k>0,∴,
∴S△POEOE×(﹣b)(﹣b),
∴对于确定的实数k,动点A在运动过程中,△POE的面积不会发生变化.
以下方法适合初二学生:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题91
班级 姓名 小组
91.如图,一次函数y1=kx+b(k≠0)与反比例函数y2(m≠0)的图象交于
点A(1,2)和B(﹣2,a),与y轴交于点M.
(1)求一次函数和反比例函数的解析式;
(2)在y轴上取一点N,当△AMN的面积为3时,求点N的坐标;
(3)将直线y1向下平移2个单位后得到直线y3,当函数值y1>y2>y3时,求x的取值范围.
每日一题92
班级 姓名 小组
92.如图,在平面直角坐标系xOy中,一次函数yx的图象与反比例函数y(x>0)的图象相交于点A(a,3),与x轴相交于点B.
(1)求反比例函数的表达式;
(2)过点A的直线交反比例函数的图象于另一点C,交x轴正半轴于点D,当△ABD是以BD为底的等腰三角形时,求直线AD的函数表达式及点C的坐标.
每日一题93
班级 姓名 小组
93.如图,直线y=kx+2与双曲线y相交于点A、B,已知点A的横坐标为1.
(1)求直线y=kx+2的解析式及点B的坐标;
(2)以线段AB为斜边在直线AB的上方作等腰直角三角形ABC.求经过点C的双曲线的解析式.
每日一题94
班级 姓名 小组
94.如图,过C点的直线与x轴,y轴分别交于点A,B两点,且BC=AB,过点C作CH⊥x轴,垂足为点H,交反比例函数(x>0)的图象于点D,连接OD,△ODH的面积为6.
(1)求k值和点D的坐标;
(2)如图,连接BD,OC,点E在直线上,且位于第二象限内,若△BDE的面积是△OCD面积的2倍,求点E的坐标.
每日一题95
班级 姓名 小组
95.已知在平面直角坐标系xOy中,点A是反比例函数y(x>0)图象上的一个动点,连结AO,AO的延长线交反比例函数y(k>0,x<0)的图象于点B,过点A作AE⊥y轴于点E.
(1)如图1,过点B作BF⊥x轴,于点F,连接EF.
①若k=1,求证:四边形AEFO是平行四边形;
②连结BE,若k=4,求△BOE的面积.
(2)如图2,过点E作EP∥AB,交反比例函数y(k>0,x<0)的图象于点P,连结OP.试探究:对于确定的实数k,动点A在运动过程中,△POE的面积是否会发生变化?请说明理由.
每日一题91 参考答案
91.解:(1)∵过点A(1,2),∴ m=1×2=2,∴反比例函数.
当x=﹣2时,a=﹣1,即B(﹣2,﹣1).
∵y1=kx+b过A(1,2)和B(﹣2,﹣1),则,解得,∴y1=x+1.
(2)当x=0时,代入y=x+1中得,y=1,即M(0,1),
∵S△AMNMN |xA|=3且xA=1,∴MN=6,∴N(0,7)或(0,﹣5).
(3)如图,设y2与y3的图像交于C,D两点,
∵y1向下平移两个单位得y3且y1=x+1,∴y3=x﹣1,
联立,解得或,∴C(﹣1,﹣2),D(2,1).
∵y1>y2>y3,∴﹣2<x<﹣1或1<x<2.
每日一题92 参考答案
92.解:(1)∵一次函数yx的图象经过点A(a,3),
∴a3,解得a=2,∴A(2,3),
将A(2,3)代入y(x>0),得:3,
∴k=6,∴反比例函数的表达式为y.
(2)如图,过点A作AE⊥x轴于点E,
在yx中,令y=0,得:x0,
解得x=﹣2,∴B(﹣2,0),
∵E(2,0),∴BE=2﹣(﹣2)=4,
∵△ABD是以BD为底边的等腰三角形,
∴AB=AD,
∵AE⊥BD,∴DE=BE=4,∴D(6,0),
设直线AD的函数表达式为y=mx+n,
∵A(2,3),D(6,0),
∴,解得,
∴直线AD的函数表达式为yx,
联立方程组:,解得(舍去),,
∴点C的坐标为(4,).
每日一题93 参考答案
解:(1)∵点A在双曲线y上,且点A的横坐标为1,
∴点A的纵坐标为,∴点A(1,),
∵点A(1,)在直线y=kx+2上,∴k+2,∴,
∴直线AB的解析式为yx+2.
联立直线AB和双曲线的解析式得,,
解得,(点A的纵横坐标)或, ∴B(3,).
(2)如图,过点A作x轴的垂线,过点B作y轴的垂线,两线相交于点F,过点C作CD⊥AF,交AF于D,过点C作CE⊥BF于E,
∴∠D=∠F=∠CEF=∠CEB=90°,∴四边形CDFE是矩形,∴∠DCE=90°,
∵∠ACB=90°,∴∠ACD=∠BCE,
∵以线段AB为斜边在直线AB的上方作等腰直角三角形ABC,
∴AC=BC,∴△ACD≌△BCE(AAS),∴AD=BE,CD=CE,
设点C(m,n),∵A(1,),B(3,),
∴AD=n,CD=m﹣1,BE=3﹣m,CE=n,
∴,∴,∴C(,2),
设过点C的双曲线的解析式为y,∴k'=25,
∴过点C的双曲线的解析式为y.
每日一题94 参考答案
解:(1)设点D坐标为(m,n),由题意得,∴mn=12.
∵点D在的图象上,∴k=mn=12.
∵直线的图象与x轴交于点A,∴点A的坐标为(-4,0).
∵CH⊥x轴,∴CH∥y轴,∴,
∴OH=AO=4,∴点D的横坐标为4,
∵点D在反比例函数的图象上,∴点D坐标为(4,3).
(2)由(1)知CD∥y轴,.
.
过点E作EFCD,垂足为点 F,交y轴于点M,
.∴点 E 的横坐标为-8.
∵点E 在直线上,∴点E的坐标为(-8,2).
每日一题95 参考答案
解:(1)①证明:设点A的坐标为(a,),则当点k=1时,点B的坐标为(﹣a,),
∴AE=OF=a,∵AE⊥y轴,∴AE∥OF,∴四边形AEFO是平行四边形;
②过点B作BD⊥y轴于点D,如图1,
∵AE⊥y轴,∴AE∥BD,∴△AEO∽△BDO,∴,
∴当k=4时,,即,∴S△BOE=2S△AOE=1;
(2)不改变.理由如下:过点P作PH⊥x轴于点H,PE与x轴交于点G,
设点A的坐标为(a,),点P的坐标为(b,),则AE=a,OE,PH,
∵四边形AEGO是平行四边形,∴∠EAO=∠EGO,AE=OG,
∵∠EGO=∠PGH,∴∠EAO=∠PGH,
又∵∠PHG=∠AEO,∴△AEO∽△GHP,∴,
∵GH=OH﹣OG=﹣b﹣a,∴,∴k=0,解得,
∵a,b异号,k>0,∴,
∴S△POEOE×(﹣b)(﹣b),
∴对于确定的实数k,动点A在运动过程中,△POE的面积不会发生变化.
以下方法适合初二学生:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
