浙教版八年级下册数学每日一题96-100(第六章 反比例函数)培优练习(含解析)
文档属性
| 名称 | 浙教版八年级下册数学每日一题96-100(第六章 反比例函数)培优练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 14:05:30 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
每日一题96
班级 姓名 小组
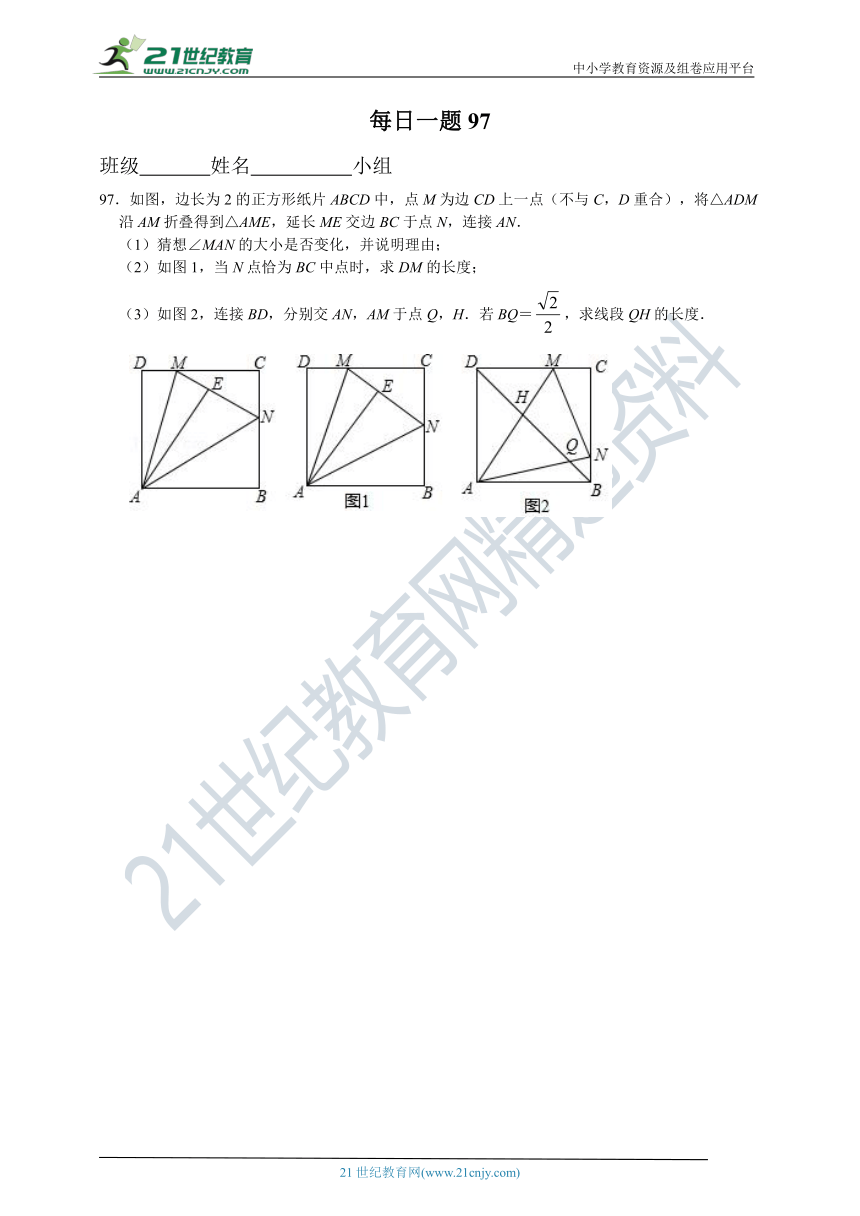
96.如图,在平面直角坐标系中,直线y=﹣x+5与反比例函数y=(x>0)的图象相交于点A(3,a)和点B(b,3),点D,C分别是x轴和y轴的正半轴上的动点,且满足CD∥AB.
(1)求a,b的值及反比例函数的解析式;
(2)若OD=1,求点C的坐标,判断四边形ABCD的形状并说明理由;
(3)若点M是反比例函数y=(x>0)图象上的一个动点,当△AMD是以AM为直角边的等腰直角三角形时,求点M的坐标.
每日一题97
班级 姓名 小组
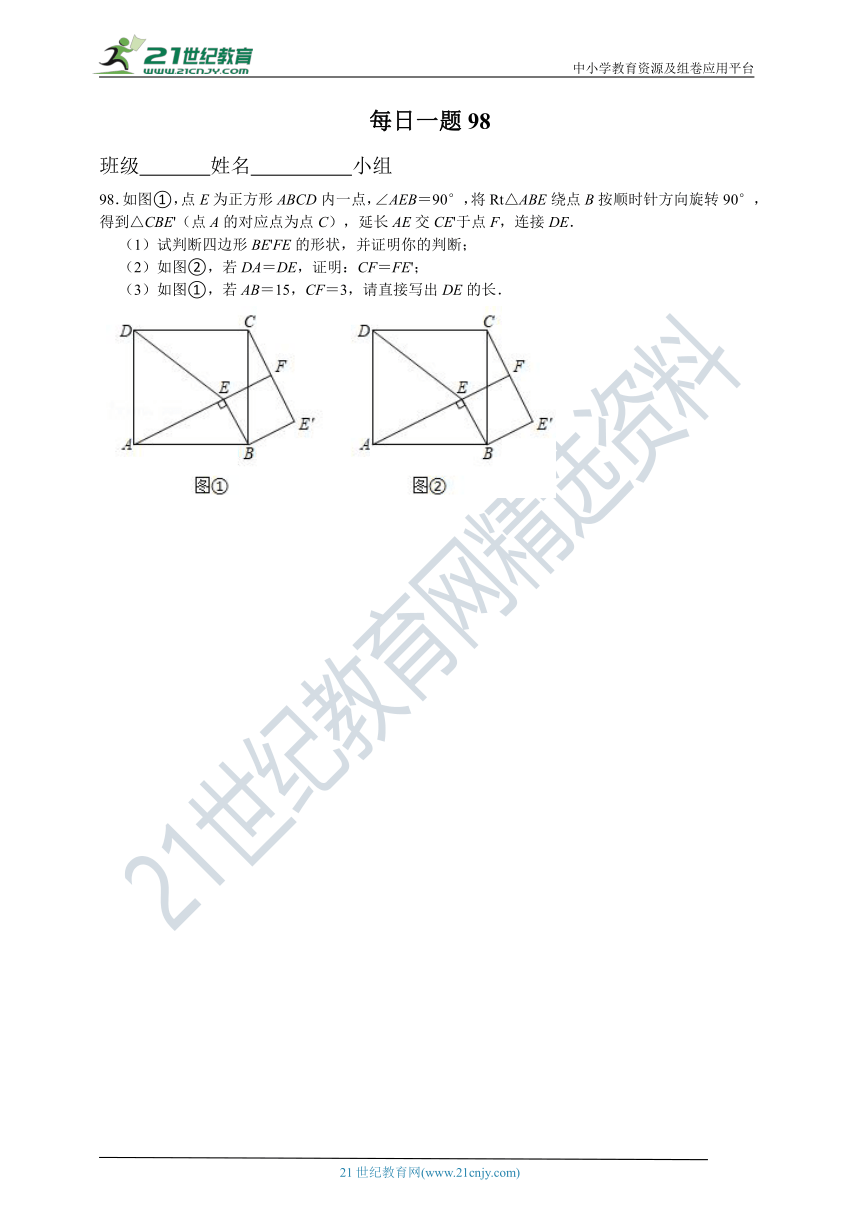
97.如图,边长为2的正方形纸片ABCD中,点M为边CD上一点(不与C,D重合),将△ADM沿AM折叠得到△AME,延长ME交边BC于点N,连接AN.
(1)猜想∠MAN的大小是否变化,并说明理由;
(2)如图1,当N点恰为BC中点时,求DM的长度;
(3)如图2,连接BD,分别交AN,AM于点Q,H.若BQ=,求线段QH的长度.
每日一题98
班级 姓名 小组
98.如图①,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE'(点A的对应点为点C),延长AE交CE'于点F,连接DE.
(1)试判断四边形BE'FE的形状,并证明你的判断;
(2)如图②,若DA=DE,证明:CF=FE';
(3)如图①,若AB=15,CF=3,请直接写出DE的长.
每日一题99
班级 姓名 小组
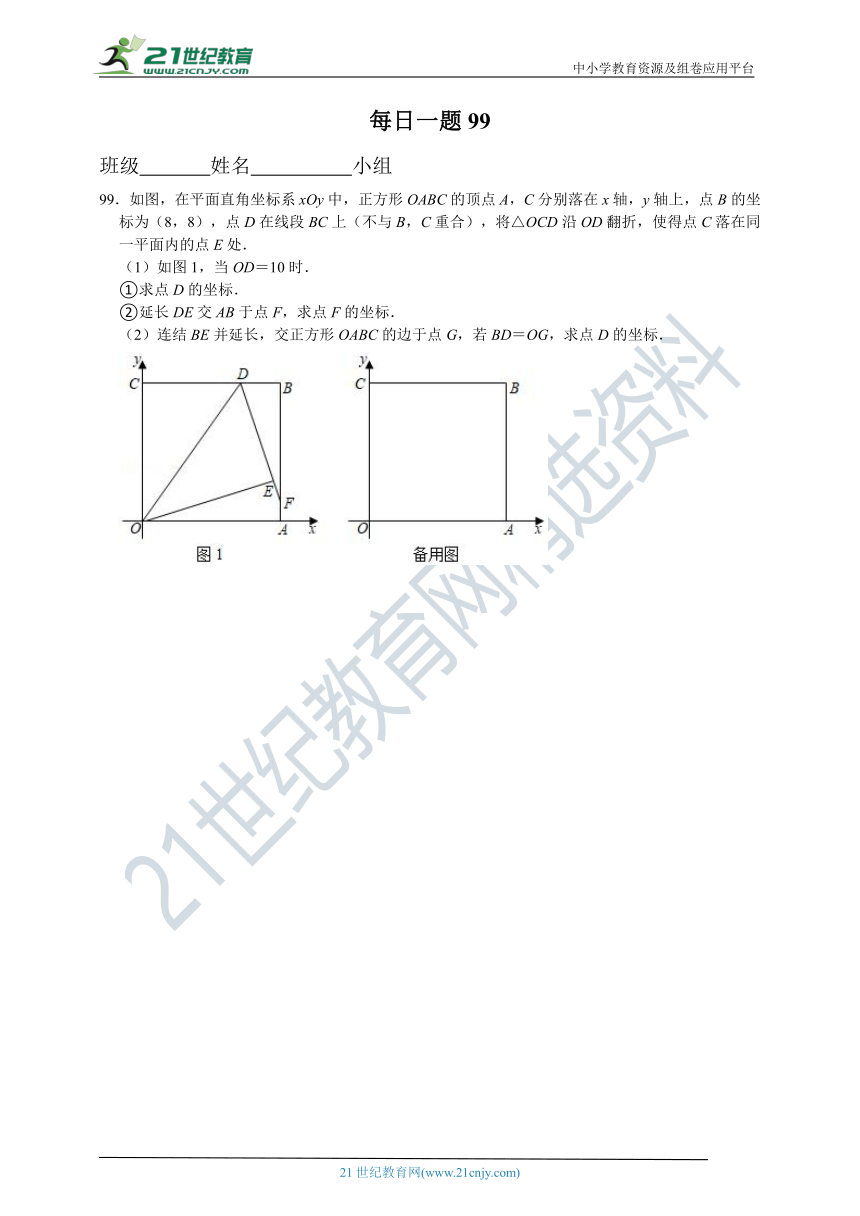
99.如图,在平面直角坐标系xOy中,正方形OABC的顶点A,C分别落在x轴,y轴上,点B的坐标为(8,8),点D在线段BC上(不与B,C重合),将△OCD沿OD翻折,使得点C落在同一平面内的点E处.
(1)如图1,当OD=10时.
①求点D的坐标.
②延长DE交AB于点F,求点F的坐标.
(2)连结BE并延长,交正方形OABC的边于点G,若BD=OG,求点D的坐标.
每日一题100
班级 姓名 小组
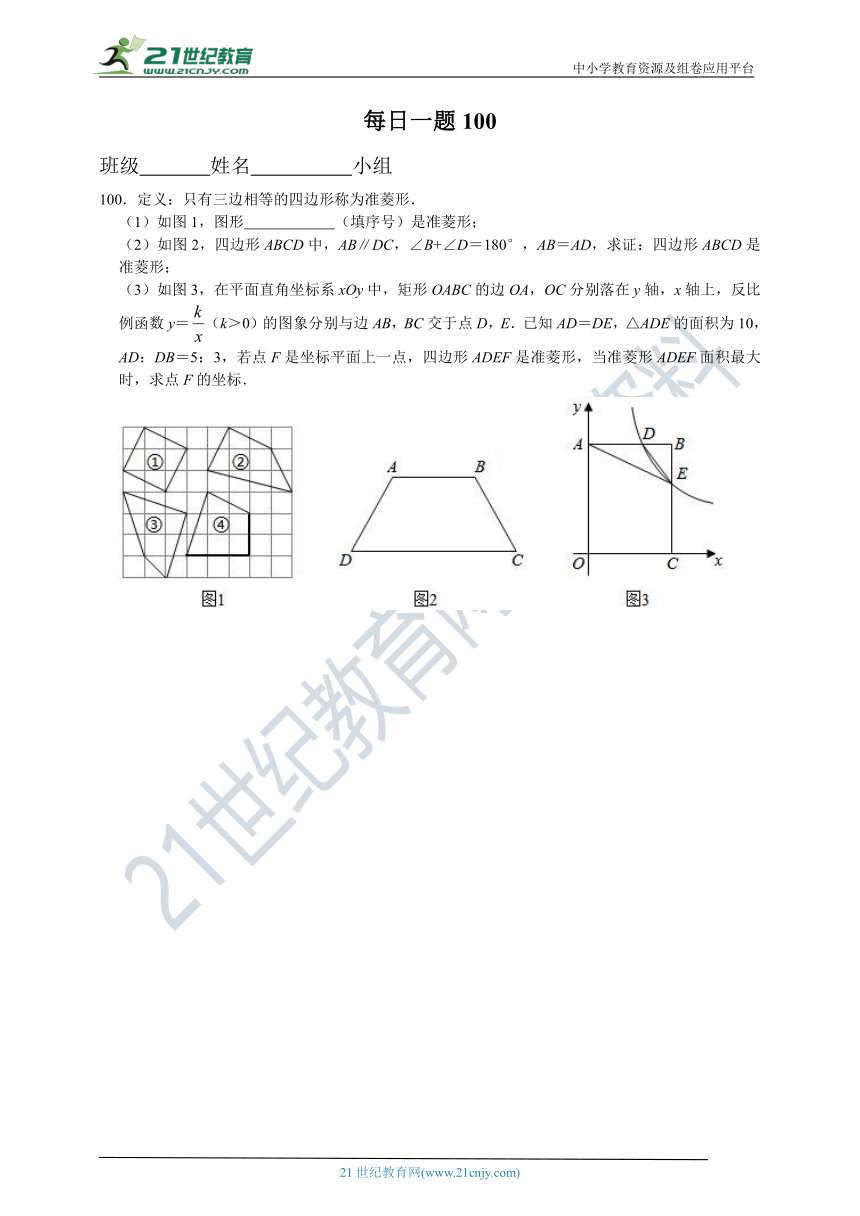
100.定义:只有三边相等的四边形称为准菱形.
(1)如图1,图形 (填序号)是准菱形;
(2)如图2,四边形ABCD中,AB∥DC,∠B+∠D=180°,AB=AD,求证:四边形ABCD是准菱形;
(3)如图3,在平面直角坐标系xOy中,矩形OABC的边OA,OC分别落在y轴,x轴上,反比例函数y=(k>0)的图象分别与边AB,BC交于点D,E.已知AD=DE,△ADE的面积为10,AD:DB=5:3,若点F是坐标平面上一点,四边形ADEF是准菱形,当准菱形ADEF面积最大时,求点F的坐标.
每日一题96 参考答案
96.解:(1)把A(3,a)和B(2,b)分别代入y=﹣x+5,得:a=2,b=3,
把A(3,2)代入,得:k=6,∴反比例函数解析式为;
(2)∵CD∥AB,∴设CD的解析式为y=﹣x+m,
∵OD=1,D在x轴的正半轴上,∴D的坐标为(1,0),
以点A、B、C、D构成的四边形是矩形,理由如下:
将D代入直接CD解析式得:y=﹣x+1,∴C的坐标为(0,1),
∵A(3,2),B(2,3),C(0,1),D(1,0),∴,
又∵AB∥CD,∴四边形ABCD是平行四边形,
如图,过点B作BE⊥y轴于点E,则E(0,3),
∴BE=CE=2,
∴△BEC和△COD都等腰直角三角形,
∴∠ECB=∠OCD=45°,
∴∠BCD=90°,
∴平行四边形ABCD是矩形;
(3)①当∠MAD=90°时,
过点A作直线l∥x轴,过点M作MQ⊥直线l于点Q,过点D作DP⊥直线l于点P,
∵∠MAD=90°,∴∠MAQ+∠PAD=90°,
∵DP⊥直线l于点P,∴∠PAD+∠PDA=90°,∴∠AQM=∠PDA,
在△MAQ与△ADP中,
,∴△MAQ≌△ADP(AAS),∴PD=AQ=2,QM=AP,
设M的坐标为(5,n),∴5n=6,则n=1.2,∴M(5,1.2);
②当∠AMD=90°时,同理,过点M作直线l∥y轴,过点A作AP⊥直线l于点P,过点D作DQ⊥直线l于点Q,可得:△MAP≌△DMQ,∴PM=DQ,QM=AP,
设M的坐标为(3+n,n),∴n(3+n)=6,
解得:,(舍去),∴,
综上所述:M的坐标为(5,1.2),.
每日一题97 参考答案
97.解:(1)∠MAN的大小没有变化,∵将△ADM沿AM折叠得到△AME,
∴△ADM≌△AEM,
∴AD=AE=2、DM=EM、∠D=∠AEM=90°、∠DAM=∠EAM=∠DAE,
又∵AD=AB=2、∠D=∠B=90°,
∴AE=AB、∠B=∠AEM=∠AEN=90°,
在Rt△BAN和Rt△EAN中,
∵,∴Rt△BAN≌Rt△EAN(HL),∴∠BAN=∠EAN=∠BAE,
则∠MAN=∠EAM+∠EAN=∠DAE+∠BAE=(∠DAE+∠BAE)=∠BAD=45°,
∴∠MAN的大小没有变化;
(2)∵N点恰为BC中点,∴EN=BN=CN=1,
设DM=EM=x,则MC=2﹣x,∴MN=ME+EN=1+x,
在Rt△MNC中,由MC2+CN2=MN2可得(2﹣x)2+12=(1+x)2,解得:x=,即DM=;
(3)如图,将△ABQ绕点A逆时针旋转90°得△ADG,连接GH,
则△ABQ≌△ADG,
∴DG=BQ=、AG=AQ、∠ADG=∠ABQ=∠ADB=45°、∠BAQ=∠DAG,
∵∠MAN=∠BAD=45°,
∴∠BAQ+∠DAM=∠DAG+∠DAM=∠GAH=45°,
则∠GAH=∠QAH,
在△GAH和△QAH中,
∵,∴△GAH≌△QAH(SAS),∴GH=QH,
设GH=QH=a,
∵BD=AB=2,BQ=,∴DQ=BD﹣BQ=,∴DH=﹣a,
∵∠ADG=∠ADH=45°,∴∠GDH=90°,
在Rt△DGH中,由DG2+DH2=GH2可得()2+(﹣a)2=a2,
解得:a=,即QH=.
每日一题98 参考答案
98.解:(1)结论:四边形BE'FE是正方形.
理由:如图①中,∵△CBE'是由Rt△ABE绕点B按顺时针方向旋转90°得到的,
∴∠CE'B=∠AEB=90°,∠EBE'=90°,又∵∠BEF+∠AEB=90°,
∴∠BEF=90°,∴四边形BE'FE是矩形,
由旋转可知 BE=BE',∴四边形BE'FE是正方形.
(2)如图②中,过点D作DH⊥AE于点H则∠AHD=90°,∠DAH+∠ADH=90°,
∵DA=DE,∴AH=EH=AE,
∵四边形ABCD是正方形,
∴AB=DA∠DAB=90°,
∴∠DAH+∠EAB=90°,
∴∠ADH=∠EAB,
在△ADH和△BAE中,
,
∴△ADH≌△BAE(AAS),∴AH=BE,
由旋转可知 AE=CE',
由(1)可知四边形BE'FE是正方形,
∴BE=E'F,
∴E'F=AH=AE=CE',
∴CF=E'F.
(3)如图1,过点D作DH⊥AE于点H.
∵△ADH≌△BAE,∴AH=BE=E'F,
∵CF=3,∵AB2=AE2+BE2,
∴225=(BE+3)2+BE2,
∴BE=9,BE=﹣12(舍去),
∴DH=AE=CE'=12,
∴EH=12﹣9=3,
在Rt△DEH中,DE===3.
每日一题99 参考答案
【解答】解:(1)①如图1,∵四边形OABC是正方形,点B的坐标为(8,8),
∴∠OCB=∠ABC=∠OAB=90°,OC=8,
∵OD=10,∴CD===6,∴D(6,8);
②如图1,连接OF,
由翻折得:∠OED=∠OCD=90°,DE=DC=6,OE=OC=8,
∴∠OEF=180°﹣∠OED=90°,
∵OA=8,∠OAF=90°,∴OA=OE,
∵OF=OF,∴Rt△OFA≌Rt△OFE(HL),∴AF=EF,
设AF=EF=a,则BF=8﹣a,DF=6+a,BD=2,
由勾股定理得:BD2+BF2=DF2,∴22+(8﹣a)2=(6+a)2,
解得:a=,∴AF=,∴F(8,);
(2)①当点G在OA边上时,如图2,连接CE,
∵四边形OABC是正方形,
∴∠OCB=∠OAB=∠ABC=∠AOC=90°,OA=AB=OC=BC=8,BC∥OA,
∵BD=OG,∴四边形ODBG是平行四边形,∴OD∥BG,
∵DE=DC,OE=OC,∴CE⊥OD,CH=HE,
∵OD∥BG,∴CE⊥BG,∴∠CEB=90°,
∴∠DCE+∠DBE=90°,∠DEC+∠DEB=90°,
∵DC=DE,∴∠DCE=∠DEC,
∴∠DBE=∠DEB,∴DB=DE,∴DB=DC=BC=4,∴D(4,8);
②当点G在OC边上时,如图3,连接CE,
过点E作EF⊥BC于点F,
由翻折得,CD=DE,∠COD=∠EOD,∠ODC=∠ODE,∠OED=∠OCD=90°,CE⊥OD,
∴∠COD+∠ODC=90°,∠DCE+∠ODC=90°,∴∠COD=∠DCE,
∵OC=BC=8,OG=BD,∴CG=CD,
在△OCD和△BCG中,
∴△OCD≌△BCG(SAS), ∴∠COD=∠CBG, ∴∠DCE=∠CBG,
∴CE=BE,∵∠DCE+∠ECG=90°,∠CBG+∠BGC=90°,
∴∠ECG=∠BGC,∴CE=EG,∴BE=EG,∵EF⊥BC,∴BF=CF=4,∴EF=CG,
设BD=a,则OG=a,DE=CD=CG=8﹣a,EF=(8﹣a),DF=a﹣4,
在Rt△DEF中,EF2+DF2=DE2,∴[(8﹣a)]2+(a﹣4)2=(8﹣a)2,
解得:a=8﹣8或a=﹣8﹣8(舍去),
∴CD=8﹣a=8﹣(8﹣8)=16﹣8,∴D(16﹣8,8);
综上所述,点D的坐标为(4,8)或(16﹣8,8).
每日一题100 参考答案
100.解:(1)∵图形①四边相等,图形②③只有三边相等,图形④四边都不相等,
∴图形②③是准菱形,故答案为:②③;
(2)如图2,延长DA,CB交于点E,
∵AB∥CD,∴∠D=∠EAB,∠EBA=∠C,
∵∠ABC+∠D=180°,∠ABC+∠ABE=180°,
∴∠D=∠ABE,∴∠EAB=∠D=∠ABE=∠C,
∴ED=EC,EA=EB,∴AD=BC,又∵AB=AD,∴AB=AD=BC,
又∵AB≠CD,∴四边形ABCD是准菱形;
(3)∵AD:DB=5:3,AD=DE,∴设AD=5x=DE,DB=3x,
∴BE===4x,
∵△ADE的面积为10,∴×AD×BE=10,∴5x×4x=20,∴x=1,
∴AD=DE=5,BE=4,DB=3,∴AB=8,
设BC=m,则点D(5,m),点E(8,m﹣4),
∵反比例函数y=(k>0)的图象分别与边AB,BC交于点D,E.∴k=5m=8(m﹣4),
解得:m=,∴点E(8,),BC=AO=,∴CE=,
∵四边形ADEF是准菱形,
∴AD=DE=EF=5或AD=DE=AF=5,
如图3,当AD=DE=EF=5时,过点F作FM⊥EC于M,过点D作DH⊥AE于H,
∵准菱形ADEF面积=S△ADE+S△AEF=10+S△AEF,
∴当EF⊥AE时,S△AEF有最大值,即准菱形ADEF面积有最大值,
∵AB=8,BE=4,
∴AE===4,
∵DE=AD,DH⊥AE,∴AH=HE=2,
∴DH===
∵∠BAE+∠AEB=90°=∠AEB+∠FEM,∴∠BAE=∠FEM,
又∵AD=EF,∠AHD=∠EMF,∴△ADH≌△EFM(AAS),
∴EM=AH=2,DH=FM=,∴CM=EC﹣EM=﹣2,
∴点F(8﹣,﹣2);
如图3,当AD=DE=AF'时,过点F'作F'N⊥AO于N,过点D作DH⊥AE于H,
同理可求△AF'N≌△ADH(AAS),
∴AN=AH=2,DH=F'N=,∴NO=﹣2,∴点F'坐标为(﹣,﹣2),
综上所述:点F的坐标为(8﹣,﹣2)或(﹣,﹣2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题96
班级 姓名 小组
96.如图,在平面直角坐标系中,直线y=﹣x+5与反比例函数y=(x>0)的图象相交于点A(3,a)和点B(b,3),点D,C分别是x轴和y轴的正半轴上的动点,且满足CD∥AB.
(1)求a,b的值及反比例函数的解析式;
(2)若OD=1,求点C的坐标,判断四边形ABCD的形状并说明理由;
(3)若点M是反比例函数y=(x>0)图象上的一个动点,当△AMD是以AM为直角边的等腰直角三角形时,求点M的坐标.
每日一题97
班级 姓名 小组
97.如图,边长为2的正方形纸片ABCD中,点M为边CD上一点(不与C,D重合),将△ADM沿AM折叠得到△AME,延长ME交边BC于点N,连接AN.
(1)猜想∠MAN的大小是否变化,并说明理由;
(2)如图1,当N点恰为BC中点时,求DM的长度;
(3)如图2,连接BD,分别交AN,AM于点Q,H.若BQ=,求线段QH的长度.
每日一题98
班级 姓名 小组
98.如图①,点E为正方形ABCD内一点,∠AEB=90°,将Rt△ABE绕点B按顺时针方向旋转90°,得到△CBE'(点A的对应点为点C),延长AE交CE'于点F,连接DE.
(1)试判断四边形BE'FE的形状,并证明你的判断;
(2)如图②,若DA=DE,证明:CF=FE';
(3)如图①,若AB=15,CF=3,请直接写出DE的长.
每日一题99
班级 姓名 小组
99.如图,在平面直角坐标系xOy中,正方形OABC的顶点A,C分别落在x轴,y轴上,点B的坐标为(8,8),点D在线段BC上(不与B,C重合),将△OCD沿OD翻折,使得点C落在同一平面内的点E处.
(1)如图1,当OD=10时.
①求点D的坐标.
②延长DE交AB于点F,求点F的坐标.
(2)连结BE并延长,交正方形OABC的边于点G,若BD=OG,求点D的坐标.
每日一题100
班级 姓名 小组
100.定义:只有三边相等的四边形称为准菱形.
(1)如图1,图形 (填序号)是准菱形;
(2)如图2,四边形ABCD中,AB∥DC,∠B+∠D=180°,AB=AD,求证:四边形ABCD是准菱形;
(3)如图3,在平面直角坐标系xOy中,矩形OABC的边OA,OC分别落在y轴,x轴上,反比例函数y=(k>0)的图象分别与边AB,BC交于点D,E.已知AD=DE,△ADE的面积为10,AD:DB=5:3,若点F是坐标平面上一点,四边形ADEF是准菱形,当准菱形ADEF面积最大时,求点F的坐标.
每日一题96 参考答案
96.解:(1)把A(3,a)和B(2,b)分别代入y=﹣x+5,得:a=2,b=3,
把A(3,2)代入,得:k=6,∴反比例函数解析式为;
(2)∵CD∥AB,∴设CD的解析式为y=﹣x+m,
∵OD=1,D在x轴的正半轴上,∴D的坐标为(1,0),
以点A、B、C、D构成的四边形是矩形,理由如下:
将D代入直接CD解析式得:y=﹣x+1,∴C的坐标为(0,1),
∵A(3,2),B(2,3),C(0,1),D(1,0),∴,
又∵AB∥CD,∴四边形ABCD是平行四边形,
如图,过点B作BE⊥y轴于点E,则E(0,3),
∴BE=CE=2,
∴△BEC和△COD都等腰直角三角形,
∴∠ECB=∠OCD=45°,
∴∠BCD=90°,
∴平行四边形ABCD是矩形;
(3)①当∠MAD=90°时,
过点A作直线l∥x轴,过点M作MQ⊥直线l于点Q,过点D作DP⊥直线l于点P,
∵∠MAD=90°,∴∠MAQ+∠PAD=90°,
∵DP⊥直线l于点P,∴∠PAD+∠PDA=90°,∴∠AQM=∠PDA,
在△MAQ与△ADP中,
,∴△MAQ≌△ADP(AAS),∴PD=AQ=2,QM=AP,
设M的坐标为(5,n),∴5n=6,则n=1.2,∴M(5,1.2);
②当∠AMD=90°时,同理,过点M作直线l∥y轴,过点A作AP⊥直线l于点P,过点D作DQ⊥直线l于点Q,可得:△MAP≌△DMQ,∴PM=DQ,QM=AP,
设M的坐标为(3+n,n),∴n(3+n)=6,
解得:,(舍去),∴,
综上所述:M的坐标为(5,1.2),.
每日一题97 参考答案
97.解:(1)∠MAN的大小没有变化,∵将△ADM沿AM折叠得到△AME,
∴△ADM≌△AEM,
∴AD=AE=2、DM=EM、∠D=∠AEM=90°、∠DAM=∠EAM=∠DAE,
又∵AD=AB=2、∠D=∠B=90°,
∴AE=AB、∠B=∠AEM=∠AEN=90°,
在Rt△BAN和Rt△EAN中,
∵,∴Rt△BAN≌Rt△EAN(HL),∴∠BAN=∠EAN=∠BAE,
则∠MAN=∠EAM+∠EAN=∠DAE+∠BAE=(∠DAE+∠BAE)=∠BAD=45°,
∴∠MAN的大小没有变化;
(2)∵N点恰为BC中点,∴EN=BN=CN=1,
设DM=EM=x,则MC=2﹣x,∴MN=ME+EN=1+x,
在Rt△MNC中,由MC2+CN2=MN2可得(2﹣x)2+12=(1+x)2,解得:x=,即DM=;
(3)如图,将△ABQ绕点A逆时针旋转90°得△ADG,连接GH,
则△ABQ≌△ADG,
∴DG=BQ=、AG=AQ、∠ADG=∠ABQ=∠ADB=45°、∠BAQ=∠DAG,
∵∠MAN=∠BAD=45°,
∴∠BAQ+∠DAM=∠DAG+∠DAM=∠GAH=45°,
则∠GAH=∠QAH,
在△GAH和△QAH中,
∵,∴△GAH≌△QAH(SAS),∴GH=QH,
设GH=QH=a,
∵BD=AB=2,BQ=,∴DQ=BD﹣BQ=,∴DH=﹣a,
∵∠ADG=∠ADH=45°,∴∠GDH=90°,
在Rt△DGH中,由DG2+DH2=GH2可得()2+(﹣a)2=a2,
解得:a=,即QH=.
每日一题98 参考答案
98.解:(1)结论:四边形BE'FE是正方形.
理由:如图①中,∵△CBE'是由Rt△ABE绕点B按顺时针方向旋转90°得到的,
∴∠CE'B=∠AEB=90°,∠EBE'=90°,又∵∠BEF+∠AEB=90°,
∴∠BEF=90°,∴四边形BE'FE是矩形,
由旋转可知 BE=BE',∴四边形BE'FE是正方形.
(2)如图②中,过点D作DH⊥AE于点H则∠AHD=90°,∠DAH+∠ADH=90°,
∵DA=DE,∴AH=EH=AE,
∵四边形ABCD是正方形,
∴AB=DA∠DAB=90°,
∴∠DAH+∠EAB=90°,
∴∠ADH=∠EAB,
在△ADH和△BAE中,
,
∴△ADH≌△BAE(AAS),∴AH=BE,
由旋转可知 AE=CE',
由(1)可知四边形BE'FE是正方形,
∴BE=E'F,
∴E'F=AH=AE=CE',
∴CF=E'F.
(3)如图1,过点D作DH⊥AE于点H.
∵△ADH≌△BAE,∴AH=BE=E'F,
∵CF=3,∵AB2=AE2+BE2,
∴225=(BE+3)2+BE2,
∴BE=9,BE=﹣12(舍去),
∴DH=AE=CE'=12,
∴EH=12﹣9=3,
在Rt△DEH中,DE===3.
每日一题99 参考答案
【解答】解:(1)①如图1,∵四边形OABC是正方形,点B的坐标为(8,8),
∴∠OCB=∠ABC=∠OAB=90°,OC=8,
∵OD=10,∴CD===6,∴D(6,8);
②如图1,连接OF,
由翻折得:∠OED=∠OCD=90°,DE=DC=6,OE=OC=8,
∴∠OEF=180°﹣∠OED=90°,
∵OA=8,∠OAF=90°,∴OA=OE,
∵OF=OF,∴Rt△OFA≌Rt△OFE(HL),∴AF=EF,
设AF=EF=a,则BF=8﹣a,DF=6+a,BD=2,
由勾股定理得:BD2+BF2=DF2,∴22+(8﹣a)2=(6+a)2,
解得:a=,∴AF=,∴F(8,);
(2)①当点G在OA边上时,如图2,连接CE,
∵四边形OABC是正方形,
∴∠OCB=∠OAB=∠ABC=∠AOC=90°,OA=AB=OC=BC=8,BC∥OA,
∵BD=OG,∴四边形ODBG是平行四边形,∴OD∥BG,
∵DE=DC,OE=OC,∴CE⊥OD,CH=HE,
∵OD∥BG,∴CE⊥BG,∴∠CEB=90°,
∴∠DCE+∠DBE=90°,∠DEC+∠DEB=90°,
∵DC=DE,∴∠DCE=∠DEC,
∴∠DBE=∠DEB,∴DB=DE,∴DB=DC=BC=4,∴D(4,8);
②当点G在OC边上时,如图3,连接CE,
过点E作EF⊥BC于点F,
由翻折得,CD=DE,∠COD=∠EOD,∠ODC=∠ODE,∠OED=∠OCD=90°,CE⊥OD,
∴∠COD+∠ODC=90°,∠DCE+∠ODC=90°,∴∠COD=∠DCE,
∵OC=BC=8,OG=BD,∴CG=CD,
在△OCD和△BCG中,
∴△OCD≌△BCG(SAS), ∴∠COD=∠CBG, ∴∠DCE=∠CBG,
∴CE=BE,∵∠DCE+∠ECG=90°,∠CBG+∠BGC=90°,
∴∠ECG=∠BGC,∴CE=EG,∴BE=EG,∵EF⊥BC,∴BF=CF=4,∴EF=CG,
设BD=a,则OG=a,DE=CD=CG=8﹣a,EF=(8﹣a),DF=a﹣4,
在Rt△DEF中,EF2+DF2=DE2,∴[(8﹣a)]2+(a﹣4)2=(8﹣a)2,
解得:a=8﹣8或a=﹣8﹣8(舍去),
∴CD=8﹣a=8﹣(8﹣8)=16﹣8,∴D(16﹣8,8);
综上所述,点D的坐标为(4,8)或(16﹣8,8).
每日一题100 参考答案
100.解:(1)∵图形①四边相等,图形②③只有三边相等,图形④四边都不相等,
∴图形②③是准菱形,故答案为:②③;
(2)如图2,延长DA,CB交于点E,
∵AB∥CD,∴∠D=∠EAB,∠EBA=∠C,
∵∠ABC+∠D=180°,∠ABC+∠ABE=180°,
∴∠D=∠ABE,∴∠EAB=∠D=∠ABE=∠C,
∴ED=EC,EA=EB,∴AD=BC,又∵AB=AD,∴AB=AD=BC,
又∵AB≠CD,∴四边形ABCD是准菱形;
(3)∵AD:DB=5:3,AD=DE,∴设AD=5x=DE,DB=3x,
∴BE===4x,
∵△ADE的面积为10,∴×AD×BE=10,∴5x×4x=20,∴x=1,
∴AD=DE=5,BE=4,DB=3,∴AB=8,
设BC=m,则点D(5,m),点E(8,m﹣4),
∵反比例函数y=(k>0)的图象分别与边AB,BC交于点D,E.∴k=5m=8(m﹣4),
解得:m=,∴点E(8,),BC=AO=,∴CE=,
∵四边形ADEF是准菱形,
∴AD=DE=EF=5或AD=DE=AF=5,
如图3,当AD=DE=EF=5时,过点F作FM⊥EC于M,过点D作DH⊥AE于H,
∵准菱形ADEF面积=S△ADE+S△AEF=10+S△AEF,
∴当EF⊥AE时,S△AEF有最大值,即准菱形ADEF面积有最大值,
∵AB=8,BE=4,
∴AE===4,
∵DE=AD,DH⊥AE,∴AH=HE=2,
∴DH===
∵∠BAE+∠AEB=90°=∠AEB+∠FEM,∴∠BAE=∠FEM,
又∵AD=EF,∠AHD=∠EMF,∴△ADH≌△EFM(AAS),
∴EM=AH=2,DH=FM=,∴CM=EC﹣EM=﹣2,
∴点F(8﹣,﹣2);
如图3,当AD=DE=AF'时,过点F'作F'N⊥AO于N,过点D作DH⊥AE于H,
同理可求△AF'N≌△ADH(AAS),
∴AN=AH=2,DH=F'N=,∴NO=﹣2,∴点F'坐标为(﹣,﹣2),
综上所述:点F的坐标为(8﹣,﹣2)或(﹣,﹣2).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
