浙教版八年级下册期末复习第6章反比例函数好题精选60题(含解析)
文档属性
| 名称 | 浙教版八年级下册期末复习第6章反比例函数好题精选60题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-15 06:56:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第6章反比例函数好题精选60题
一.选择题(共15小题)
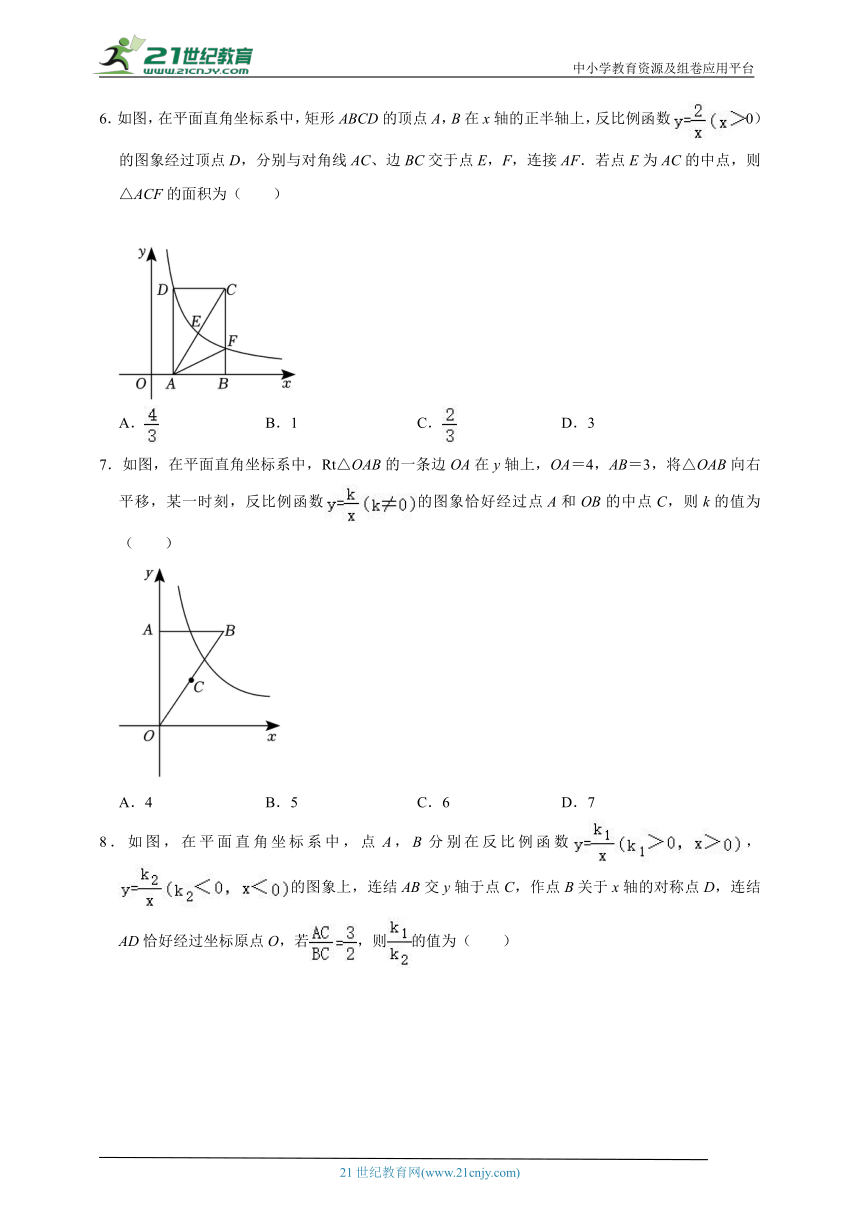
1.已知反比例函数的图象经过点(2,3),则下列描述正确的是( )
A.y的值随x值的增大而减小
B.图象位于第二、四象限
C.当x>0时,y<0
D.点(3,2)在图象上
2.若点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数的图象上,若x1<x2<0<x3则y1,y2,y3的大小关系是( )
A.y2<y1<y3 B.y3<y2<y1 C.y1<y2<y3 D.y3<y1<y2
3.如图,点A(m,m+1),B(m+3,m﹣1)都在反比例函数的图象上,则k的值为( )
A.3 B.6 C.14 D.12
4.若A(﹣3,y1),B(﹣1,y2),C(2,y3)都在函数的图象上,则( )
A.y2<y1<y3 B.y3<y2<y1 C.y1<y2<y3 D.y3<y1<y2
5.如图,菱形ABCD的对角线AC,BD交于点P,且AC过原点O,AB∥x轴,点C的坐标为(12,6),反比例函数的图象经过A,P两点,则k的值是( )
A.12 B.9 C.8 D.2
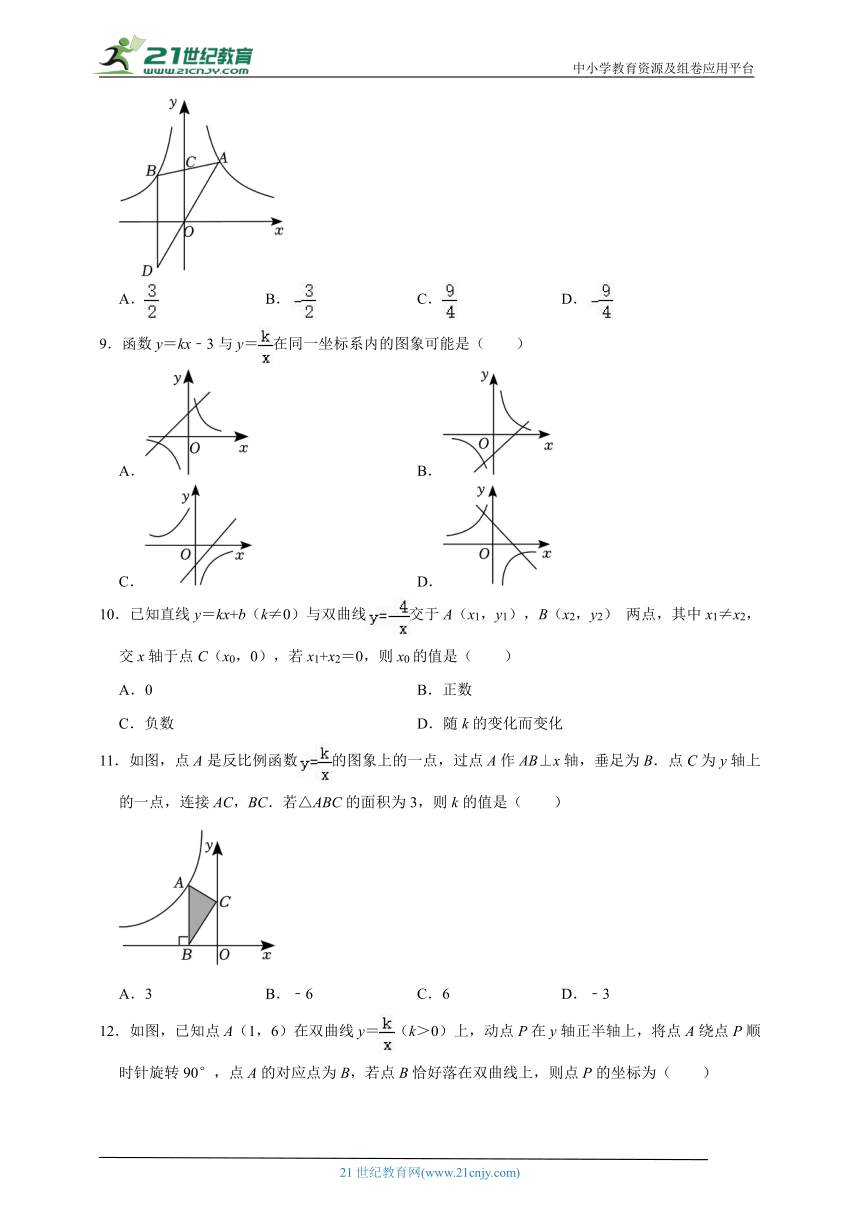
6.如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数0)的图象经过顶点D,分别与对角线AC、边BC交于点E,F,连接AF.若点E为AC的中点,则△ACF的面积为( )
A. B.1 C. D.3
7.如图,在平面直角坐标系中,Rt△OAB的一条边OA在y轴上,OA=4,AB=3,将△OAB向右平移,某一时刻,反比例函数的图象恰好经过点A和OB的中点C,则k的值为( )
A.4 B.5 C.6 D.7
8.如图,在平面直角坐标系中,点A,B分别在反比例函数,的图象上,连结AB交y轴于点C,作点B关于x轴的对称点D,连结AD恰好经过坐标原点O,若,则的值为( )
A. B. C. D.
9.函数y=kx﹣3与y=在同一坐标系内的图象可能是( )
A. B.
C. D.
10.已知直线y=kx+b(k≠0)与双曲线交于A(x1,y1),B(x2,y2) 两点,其中x1≠x2,交x轴于点C(x0,0),若x1+x2=0,则x0的值是( )
A.0 B.正数
C.负数 D.随k的变化而变化
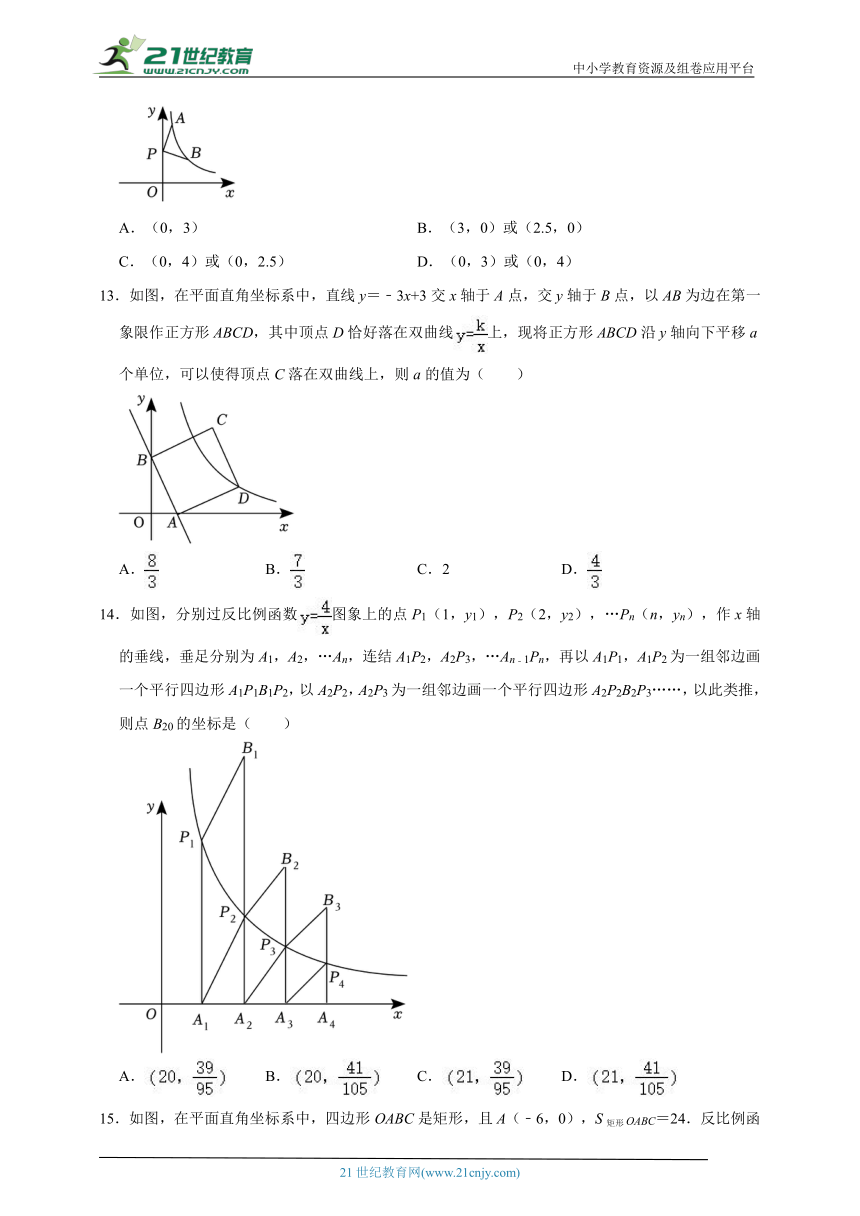
11.如图,点A是反比例函数的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
A.3 B.﹣6 C.6 D.﹣3
12.如图,已知点A(1,6)在双曲线y=(k>0)上,动点P在y轴正半轴上,将点A绕点P顺时针旋转90°,点A的对应点为B,若点B恰好落在双曲线上,则点P的坐标为( )
A.(0,3) B.(3,0)或(2.5,0)
C.(0,4)或(0,2.5) D.(0,3)或(0,4)
13.如图,在平面直角坐标系中,直线y=﹣3x+3交x轴于A点,交y轴于B点,以AB为边在第一象限作正方形ABCD,其中顶点D恰好落在双曲线上,现将正方形ABCD沿y轴向下平移a个单位,可以使得顶点C落在双曲线上,则a的值为( )
A. B. C.2 D.
14.如图,分别过反比例函数图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn),作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An﹣1Pn,再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3……,以此类推,则点B20的坐标是( )
A. B. C. D.
15.如图,在平面直角坐标系中,四边形OABC是矩形,且A(﹣6,0),S矩形OABC=24.反比例函数的图象与边AB,BC交于点D,E,连接DE,DC,则当△DCE的面积最大时,k的值为( )
A.﹣24 B.﹣12 C.﹣6 D.﹣4
二.填空题(共25小题)
16.函数的图象上有两点P1(﹣1,y1),P2(﹣2,y2),若y1<y2,写出一个符合题意的k的值: .
17.若反比例函数y=(m+2)x|m|﹣5的图象在第一、三象限,则m的值为 .
18.某商场销售一批散装坚果,进价为30元每斤,在销售时售货员发现坚果的日销量和每斤的利润正好成反比例关系,且价格调整为每斤50元时,当日销量为80斤,那么每日该坚果的销量y(单位:斤)与每斤价格x(单位:元)之间的函数表达式为 .
19.如图,反比例函数的图象与Rt△BOC的斜边OB交于点A,与边BC交于点D,若,且S△BOD=21,则k= .
20.如图,直线y=kx(k<0)与双曲线交于 A(x1,y1)、B(x2,y2)两点,则2x1y2﹣5y2x1的值为 .
21.如图,在△AOB中,AO=AB,点B在x轴上,C、D分别为OA、OB的中点,连接CD,E为CD上任意一点,连接AE、BE,反比例函数的图象经过点A.若△ABE的面积为8,则k的值为 .
22.如图,在平面直角坐标系xOy中,直线y=x与反比例函数的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交x轴于点C,交反比例函数图象于点B,若,则b的值为 .
23.如图, ABCD的顶点B,D在x轴上,AB⊥BD,反比例函数y=的图象经过点A,连接CA并延长交y轴于点E,连接DE,若△ADE的面积为2,则k的值为 .
24.近视眼镜的镜片是凹透镜,研究发现,近视眼镜的度数y(度)与镜片焦距x(米)的关系近似满足,小宇原来佩戴400度近视眼镜,经过一段时间的矫正治疗,复查验光时,所配镜片焦距调整为0.4米,则小宇的眼镜度数 (填“上涨”或“下降”)了 度.
25.某校科技小组进行野外考察,利用铺垫木板的方式通过了一片烂泥湿地,这是因为人和木板对湿地的压力F一定时,人和木板对地面的压强p(Pa)与木板面积S(m2)存在函数关系:(如图所示)若木板面积为0.2m2,则压强为 Pa.
26.如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,4),顶点C的坐标为(3,1),若反比例函数的图象与矩形ABCD有公共点,则k的值可以是 .(写出一个即可)
27.已知反比例函数的表达式为,A(x1,y1)和B(x2,y2)是反比例函数图象上两点,若x1<0<x2时,y1<y2,则m的取值范围是 .
28.小海利用杠杆平衡原理称药品质量(杠杆平衡时,动力×动力臂=阻力×阻力臂):如图1,小海发现天平平衡时左盘药品为m克,右盘砝码重20克;如图2,仍旧利用此杠杆,小海将砝码放在左盘,药品放在右盘,此时天平仍旧平衡,测得砝码重5克,右盘药品为n克.则m与n满足的关系式为 .
29.如图,一次函数y=ax+8与反比例函数的图象交于M(m,6)和N(n,2)两点,已知S△MON=8,则k= .
30.如图,已知第一象限的双曲线与正方形OCAE的两边相交于D、B两点,直线过B点.则DE:AD的值是 .
31.如图,已知点M(1,2),N(4,n)(n>0),点P为线段MN上的一个动点,反比例函数(k为常数,x>0)的图象经过点P.
(1)当点P与点M重合时,k= ;
(2)若点P与点N重合时,k=8,此时点Q(0,﹣9)到直线MN的距离为 .
32.如图,点A、D分别在函数图象上,点B、C在x轴上,若四边形ABCD为正方形,且点A在第二象限,则点A的坐标为 .
33.已知反比例函数y=,当2≤x<5时,y的取值范围是 .
34. 如图,△ABC的顶点A在反比例函数 的图象上,顶点C在y轴上,AB∥y轴,若点B的坐标为(﹣2,2),S△ABC=4,则k的值为 .
35.如图,在平面直角坐标系中,反比例函数(k为常数,k≠0)的图象经过 ABCD的顶点B,AB交y轴于点E,AB∥x轴,F为CD边上一点,AE:CF:DF=1:2:3,连结FA并延长交x轴于点G,连结DG.
(1)设△ADF的面积S1,四边形ABCF的面积为S2,则S1:S2的值为 ;
(2)当△ADG的面积为3时,k的值为 .
36.如图,A,B为反比例函数第一象限图象上任意两点,连结BO并延长交反比例函数图象另一支于点C,连结AC交x轴于点F,交y轴于点G,连结BG,连结AB并向两侧延长分别交x轴于点E,交y轴于点D.已知,S△OBG=3,则= ,k的值为 .
37.如图,在平面直角坐标系中,放置一个等腰Rt△ABC纸片,∠A=90°,BC边与x轴重合,点A坐标为(3,2),若反比例函数与AB边交于点D,与AC边交于点E.
(1)当点D为AB中点时,反比例函数的表达式为 ;
(2)将如图放置的△ABC纸片的∠B沿过点D的直线翻折,当点B落到AC中点时,k= ;
(3)若双曲线与折线AD、AE所围成的区域内(含边界)有2个横纵坐标都是整数的点,则k的取值范围是 .
38.如图,点A,B分别在第一,二象限的反比例函数图象y=(k1>0),y=(k2<0)上,点C在y轴负半轴上,连结AB,OA,AC,且AC交x轴于点E.已知AB=2AC,CE=2AE,且∠AOC=135°.若AC⊥AB,且k1+k2=﹣,则k2的值为 .
39.已知过原点的一条直线l与反比例函数的图象交于A,B两点(A在B的右侧).C是反比例函数图象上位于A点上方的一动点,连接AC并延长交y轴于点D,连接CB交y轴于点E.若AC=mCD,BC=nCE,则m﹣n= .
40.如图,在平面直角坐标系中,菱形OABC的边OC在x轴负半轴上,函数y=(x<0)的图象经过顶点A和对角线OB的中点M,作AN∥OB交y轴于点N,若△CMN的面积为6,则k的值为 .
三.解答题(共20小题)
41.已知反比例函数的图象经过点A(﹣4,﹣2).
(1)求反比例函数表达式;
(2)若点在该函数图象上,求m的值.
42.为了预防H1N1甲型流感,某校对教室采取喷洒药物消毒,在对某教室进行消毒的过程中,先经过5分钟的集中药物喷洒,再封闭教室10分钟,然后打开门窗进行通风,室内每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(分钟)之间的函数关系,在药物喷洒和封闭教室期间,y与x均满足一次函数的关系,在打开门窗通风后y与x满足反比例函数的关系,如图所示.
(1)研究表明,室内空气中的含药量低于3mg/m3时方可进入教室,从封闭教室开始,至少经过多少分钟后学生方可返回教室?
(2)当室内空气中的含药量不低于6mg/m3且特续时间不低于15分钟时,才能完全有效杀灭流感病毒.试通过分析判断此次消毒是否完全有效?
43.如图是某型号冷柜循环制冷过程中温度变化的部分示意图.该冷柜的工作过程是:当冷柜温度达到﹣4℃时制冷开始,温度开始逐渐下降,当温度下降到﹣20℃时制冷停止,温度开始逐渐上升,当温度上升到﹣4℃时,制冷再次开始,…,按照以上方式循环工作.通过分析发现,当0≤x<4时,温度y是时间x的一次函数;当4≤x<t时,温度y是时间的反比例函数.
(1)求t的值;
(2)当前冷柜的温度﹣10℃,经过多长时间温度下降到﹣20℃?
44.如图在平面直角坐标系中,一次函数y=kx+b的图象经过点A(0,﹣4)、B(2,0)交反比例函数的图象于点C(3,a),点P在反比例函数的图象上,横坐标为n(0<n<3),PQ∥y轴交直线AB于点Q,连接OP、OQ.
(1)求一次函数和反比例函数的表达式;
(2)求△OPQ面积的最大值.
45.在平面直角坐标系xOy中,直线y1=﹣2x+1与反比例函数图象的一个交点为点M.
(1)当点M的坐标为(2,m)时,求k的值;
(2)当x<﹣1时,对于x的每一个值,都有y1>y2,求k的取值范围.
46.如图,已知正比例函数y1=x的图象与反比例函数y2=的图象相交于点A(3,n)和点 B.
(1)求n和k的值;
(2)请结合函数图象,直接写出不等式x﹣<0的解集;
(3)如图,以AO为边作菱形AOCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE、OE,求△AOE的面积.
47.已知直线y1=k1x+b与双曲线相交于点P(﹣2,1)、Q(1,m).
(1)求k1,b,k2的值;
(2)在同一坐标系中画出直线y1=k1x+b与双曲线,根据图写出不等式k1x+b的解集.
48.已知反比例函数(k为常数,k≠0)与正比例函数y2=x的图象有一个交点为P(3,m).
(1)求k的值;
(2)将点P向下平移6个单位,再向左平移5个单位后,得点P′,试判断点P′是否在函数y1的图象上,并说明理由;
(3)当y1>y2时,利用函数图象直接写出自变量x的取值范围.
49.如图,已知点A(1,4),B(7,1),点P作线段AB上,并且点P的横、纵坐标均为整数.经过点P的双曲线为.
(1)当点P与点B重合时,求L的表达式;
(2)求线段AB所在直线的函数表达式;
(8)直接写出k的最小值和最大值.
50.如图,一次函数y=kx+b(k≠0)与反比例函数的图象交于点A(3,4),B(a,﹣2).
(1)求一次函数和反比例函数的解析式;
(2)求不等式的解集;
(3)连接BO并延长,交反比例函数图象于点C,连接AC,求△ABC的面积.
51.如图,在平面直角坐标系中,反比例函数y=(x>0)与一次函数y=ax+b(a≠0)的图象相交于点A(2,m)与点B(4,2).
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上是否存在一点P,使得AP+BP最小,若存在,求出点P坐标;若不存在,请说明理由.
52.在平面直角坐标系中,已知一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,且与反比例函数的图象在第一象限内交于P,K两点,连接OP,△OAP的面积为.
(1)求一次函数与反比例函数的解析式;
(2)若C为线段OA上的一个动点,当PC+KC最小时,求△PKC的面积.
53.如图,在Rt△ABC中,AC=8,BC=4,AC⊥x轴,垂足为C,AB边与y轴交于点D,反比例函数的图象经过点A.
(1)若点D是AB边的中点,求直线AB和反比例函数的表达式.
(2)将AB边沿AC边所在直线翻折,交反比例函数的图象于点E,交x轴于点F,若点E的纵坐标为2,求k的值.
54.如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=的图象交于A、B两点,已知点A的坐标是(﹣2,m+3),点B的坐标是(4,m).
(1)求反比例函数与一次函数的表达式;
(2)求△AOB的面积;
(3)当kx+b>时,x的取值范围是 .
55.如图,一次函数y=﹣2x+1与反比例函数的图象在第二象限交于点A,且点A的横坐标为﹣1.
(1)求反比例函数的解析式;
(2)点B的坐标是(﹣2,0),若点P在y轴上,且△AOP的面积与△AOB的面积相等,求点P的坐标.
56.如图1,有一块边角料ABCDE,其中AB,BC,DE,EA是线段,曲线CD可以看成反比例函数图象的一部分.小宁想利用这块边角料截取一个面积最大的矩形MNQP,其中M,N在AE上(点M在点N左侧),点P在线段BC上,点Q在曲线CD上.测量发现:∠A=∠E=90°,AE=5,AB=DE=1,点C到AB,AE所在直线的距离分别为2,4.
(1)小宁尝试建立坐标系来解决该问题,通过思考,他把A,B,C,D,E这5个点先描到平面直角坐标系上,记点A的坐标为(﹣1,0);点B的坐标为(﹣1,1).
请你在图2中补全平面直角坐标系并画出图形ABCDE;
(2)求直线BC,曲线CD的解析式;
(3)求矩形MNQP的最大面积.
57.如图,在平面直角坐标系xOy中,直线l:y=x+b与x轴、y轴分别交于点A、B,与双曲线H:y=交于点P(2,),直线x=m分别与直线l和双曲线H交于点E、D.
(1)求k和b的值;
(2)当点E在线段AB上时,如果ED=BO,求m的值;
(3)如果△BDE是以BE为腰的等腰三角形,求点E的坐标.
58.如图,已知直线y=x﹣2与x轴交于A点,与y轴交于B点,P(m,n)为双曲线上一动点,过P点分别作x轴,y轴的垂线,垂足分别为C,D,射线PC交直线AB于点E,射线PD交直线AB于点F.
(1)当DF=PC时,求m的值;
(2)连接OE,OF,求证:∠EOF的度数为45°;
(3)在双曲线上有一点Q(不与点P重合),连接PQ,有PQ∥AB,将线段PQ沿直线AB翻折得到线段P′Q′.若线段P′Q′与坐标轴没有交点,求此时n的取值范围.
59.一次函数y=﹣2x+6与反比例函数(k>0,k为常数)的图象交点为A(a,4)和点B,点C是反比例函数(k>0,k为常数)在第三象限内的图象上一点.
(1)求反比例函数的解析式和点B的坐标;
(2)若点C为直线OB与反比例函数的另一个交点,求△ACB的面积;
(3)我们将对角线相等且互相垂直的四边形称为“等直四边形”.如图2,在平面内一点D,AB∥CD,且四边形ABCD为“等直四边形”,求点C的坐标.
60.一、问题背景:
数学活动课上,老师拿出一个由五连格边长为1的正方形连成的L形教具,将它放入一个的直角三角形中,
∠BCA=90°,∠B=30°,如图1顶点D,E,F,G刚好落在三边上,请求出此直角三角形的面积.
二、问题提出与解决:(以下问题二选一解答)
(1)小颖同学受到启发,将此教具放入如图的直角坐标系中,顶点A,B,C分别落在坐标轴上,提出问题:如图2,如果反比例函数图象经过顶点D,试求出反比例解析式.
(2)小明同学也受到启发,画了一个圆,如图3,将此教具放入圆内,使圆经过其顶点A,B,C,提出问题:怎么算出圆的面积?
参考答案与试题解析
一.选择题(共15小题)
1.已知反比例函数的图象经过点(2,3),则下列描述正确的是( )
A.y的值随x值的增大而减小
B.图象位于第二、四象限
C.当x>0时,y<0
D.点(3,2)在图象上
【分析】根据已知求出k,再根据反比例函数的性质逐一判断即可.
【解答】解:∵反比例函数的图象经过点(2,3),
∴k=2×3=6,
∴在每个象限内,y的值随x值的增大而减小,
而A缺少在每个象限这个条件,故A错误;
∵k>0,
∴图象位于一、三象限,故B错误;
当x>0时,y<0,满足第四项象限特征,故C错误;
点(3,2)满足3×2=6=k,故D正确.
故选:D.
【点评】本题考查了反比例函数的图象及性质,求出k值是解题关键.
2.若点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数的图象上,若x1<x2<0<x3则y1,y2,y3的大小关系是( )
A.y2<y1<y3 B.y3<y2<y1 C.y1<y2<y3 D.y3<y1<y2
【分析】先根据反比例函数y=﹣的中k的符号判断出此函数图象所在象限,再根据x1<x2<0<x3判断出y1,y2,y3的大小关系即可.
【解答】解:∵反比例函数y=﹣中,k=﹣1<0,
∴此函数图象在二四象限,且在每一象限内y随x的增大而增大,
∵x1<x2<0<x3,
∴y3<0,y3<0<y1<y2,
∴y3<y1<y2.
故选:D.
【点评】本题考查的是反比例函数图象上点的坐标特点,根据函数解析式判断出函数图象所在的象限是解答此题的关键.
3.如图,点A(m,m+1),B(m+3,m﹣1)都在反比例函数的图象上,则k的值为( )
A.3 B.6 C.14 D.12
【分析】根据同一反比例函数图象上横纵坐标的积为定值解答即可.
【解答】解:∵点A(m,m+1),B(m+3,m﹣1)都在反比例函数的图象上,
∴m(m+1)=(m+3)(m﹣1),
解得m=3,
∴点A(3,4),B(6,2),
∴k=3×4=12,
故选:D.
【点评】本题考查反比例函数图象和性质,熟练掌握同一反比例函数图象上点的横纵坐标的积都相等,都等于反比例函数的比例系数.
4.若A(﹣3,y1),B(﹣1,y2),C(2,y3)都在函数的图象上,则( )
A.y2<y1<y3 B.y3<y2<y1 C.y1<y2<y3 D.y3<y1<y2
【分析】根据反比例函数图象的性质判断出点的位置,再利用函数特点具体判断即可.
【解答】解:∵k=2023>0,
∴函数图象位于一、三象限,
∵﹣3<0,﹣1<0,2>0,
∴点A、B在第三象限,点C在第一象限,
∴y3为正,y1、y2为负,
∵每个象限内,y随x的增大而减小,且﹣3<﹣1,
∴y1>y2,
∴y2<y1<y3,
故选:A.
【点评】本题考查了反比例函数图象的性质,灵活的运用函数图象的性质是解题的关键.
5.如图,菱形ABCD的对角线AC,BD交于点P,且AC过原点O,AB∥x轴,点C的坐标为(12,6),反比例函数的图象经过A,P两点,则k的值是( )
A.12 B.9 C.8 D.2
【分析】先根据反比例函数的对称性和菱形的性质得到,,进而求得点P坐标即可求解.
【解答】解:∵菱形ABCD的对角线AC,BD交于点P,
∴AP=PC,
∵反比例函数的图象经过A,P两点,
∴,则,
过点P、C分别作CE⊥x轴,PF⊥x轴,垂足为E,F,则PF∥CE,
∴△OPF∽△OCE,
∴,
∵点C的坐标为(12,6),
∴OE=12,CE=6,
∴OF=4,PF=2
∴点P坐标为(4,2),
∴k=4×2=8,
故选:C.
【点评】本题考查了反比例函数与几何综合,解决本题的关键是综合利用相似三角形的判定和性质、反比例函数的图象和性质、菱形的性质等,属于基础综合题型,难度适中.
6.如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数0)的图象经过顶点D,分别与对角线AC、边BC交于点E,F,连接AF.若点E为AC的中点,则△ACF的面积为( )
A. B.1 C. D.3
【分析】设D(m,),根据已知条件表示出点E(2m,),点F(3m,),易得CF=,AB=2m,根据三角形面积公式即可得到S△ACF===.
【解答】解:设D(m,),
∵ABCD是矩形,且点E为AC的中点,
∴E点纵坐标为,
代入反比例函数解析式得x=2m,
∴E(2m,),
∴B点横坐标为3m,
∴F点横坐标为3m,代入反比例函数解析式,
得y=,
∴F(3m,),
∴CF=﹣=,
∵AB=3m﹣m=2m,
∴S△ACF===,
故选:A.
【点评】本题主要考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,矩形的性质,设D点坐标根据中点坐标公式表示线段CF和AB的长是解决本题的关键.
7.如图,在平面直角坐标系中,Rt△OAB的一条边OA在y轴上,OA=4,AB=3,将△OAB向右平移,某一时刻,反比例函数的图象恰好经过点A和OB的中点C,则k的值为( )
A.4 B.5 C.6 D.7
【分析】根据题意表示出平移后的点A(a,4),C(+a,2),代入即可求得k的值.
【解答】解:∵Rt△OAB的一条边OA在y轴上,OA=4,AB=3,
∴A(0,4),B(3,4),
∴OB的中点C(,2),
设△OAB向右平移a个单位,则平移后的点A(a,4),C(+a,2),
∵反比例函数的图象恰好经过点A(a,4),C(+a,2),
∴k=4a=2(+a),
解得a=,
∴k=4a=6,
故选:C.
【点评】本题考查了反比例函数图象上点的坐标特征,坐标于图形的变化﹣平移,正确表示出点的坐标是解题的关键.
8.如图,在平面直角坐标系中,点A,B分别在反比例函数,的图象上,连结AB交y轴于点C,作点B关于x轴的对称点D,连结AD恰好经过坐标原点O,若,则的值为( )
A. B. C. D.
【分析】作AE⊥x轴于E,设A(m,),B(n,),则OE=m,AE=,OF=﹣n,FD=FB=,由题意可知BD∥OC,根据平行线分线段成比例定理得出,通过证得△ODF∽△OAE,得出,即可得出,解得=﹣.
【解答】解:作AE⊥x轴于E,
∵点B、D关于x轴的对称,
∴BD⊥x轴,
∴BD∥OC,
∴,
∵AE∥BD,
∴△ODF∽△OAE,
∴,
设A(m,),B(n,),则OE=m,AE=,OF=﹣n,FD=FB=,
∴,
∴=﹣.
故选:D.
【点评】本题考查了反比例函数图象上点的坐标特征,反比例函数的性质,关于x轴对称的点的坐标,三角形相似的判定和性质,正确表示出线段的长度是解题的关键.
9.函数y=kx﹣3与y=在同一坐标系内的图象可能是( )
A. B.
C. D.
【分析】根据当k>0、当k<0时,y=kx﹣3和y=(k≠0)经过的象限,二者一致的即为正确答案.
【解答】解:∵当k>0时,y=kx﹣3过一、三、四象限,反比例函数y=过一、三象限,
当k<0时,y=kx﹣3过二、三、四象限,反比例函数y=过二、四象限,
∴B正确;
故选:B.
【点评】本题主要考查了反比例函数的图象性质和一次函数的图象性质,关键是由k的取值确定函数所在的象限.
10.已知直线y=kx+b(k≠0)与双曲线交于A(x1,y1),B(x2,y2) 两点,其中x1≠x2,交x轴于点C(x0,0),若x1+x2=0,则x0的值是( )
A.0 B.正数
C.负数 D.随k的变化而变化
【分析】根据直线l与x轴交于C(x0,0),当得到x0=﹣,解方程组,得到kx2+bx+4=0,于是得到x1+x2=﹣,即可得到x1+x2=x0,由x1+x2=0,即可得到x0=0.
【解答】解:直线l:y=kx+b(k≠0)交x轴于C(x0,0),
∴x0=﹣,
由消去y得到kx+b=﹣,
∴kx2+bx+4=0,
∴x1+x2=﹣,
∴x1+x2=x0,
∵x1+x2=0,
∴x0=0.
故选:A.
【点评】本题考查了反比例函数与一次函数的交点问题,熟知函数与方程的关系是解题的关键.
11.如图,点A是反比例函数的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
A.3 B.﹣6 C.6 D.﹣3
【分析】连接OA,如图,利用三角形面积公式得到S△OAB=S△CAB=3,再根据反比例函数的比例系数k的几何意义得到=3,然后去绝对值即可得到满足条件的k的值.
【解答】解:连接OA,如图,
∵AB⊥x轴,
∴OC∥AB,
∴S△OAB=S△CAB=3,
而S△OAB=|k|,
∴=3,
∵k<0,
∴k=﹣6.
故选:B.
【点评】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
12.如图,已知点A(1,6)在双曲线y=(k>0)上,动点P在y轴正半轴上,将点A绕点P顺时针旋转90°,点A的对应点为B,若点B恰好落在双曲线上,则点P的坐标为( )
A.(0,3) B.(3,0)或(2.5,0)
C.(0,4)或(0,2.5) D.(0,3)或(0,4)
【分析】先把A(1,6)代入反比例函数y=(k>0)求出k的值,分别过A、B两点作x轴的垂线AC,BD,由旋转的性质证明△APC≌△PBD,再设P(0,m),即可得出B的坐标,由双曲线上的点横坐标与纵坐标的积即相等,列方程求m的值,确定P点坐标.
【解答】解:分别过A、B两点作AC⊥y轴,BD⊥y轴,垂足为C、D,
∵点A(1,6)在双曲线y=(k>0)上,
∴k=1×6=6,
∴反比例函数的解析式为y=,
∵∠APB=90°,
∴∠APC+∠BPD=90°,
又∠APC+∠PAC=90°,
∴∠PAC=∠BPD,
在△APC和△PBD中,
,
∴△APC≌△PBD(AAS),
∴CP=BD,AC=PD=1,
设P(0,m),
∴OP=m,
∴PC=6﹣m,
∴B(6﹣m,m﹣1),
∵点B在双曲线上,
∴m﹣1=,
解得m=3或m=4,
∴P(0,3)或(0,4).
故选:D.
【点评】本题考查的是反比例函数图象上点的坐标特点,坐标与图形变化﹣旋转,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
13.如图,在平面直角坐标系中,直线y=﹣3x+3交x轴于A点,交y轴于B点,以AB为边在第一象限作正方形ABCD,其中顶点D恰好落在双曲线上,现将正方形ABCD沿y轴向下平移a个单位,可以使得顶点C落在双曲线上,则a的值为( )
A. B. C.2 D.
【分析】作CE⊥y轴于点E,作DF⊥x轴于点F,作CH⊥x轴于点H,交双曲线于点G,由函数解析式确定B的坐标是(0,3),A的坐标是(1,0),根据全等三角形的判定和性质得出△OAB≌△FDA≌△BEC,AF=OB=EC=3,DF=OA=BE=1,结合图形求解即可.
【解答】解:作CE⊥y轴于点E,作DF⊥x轴于点F,作CH⊥x轴于点H,交双曲线于点G
在y=﹣3x+3中,
令x=0,解得:y=3,
即B的坐标是(0,3),
令y=0,解得:x=1,
即A的坐标是(1,0),
则OB=3,OA=1.
∵∠BAD=90°,
∴∠BAO+∠DAF=90°,
∵直角△ABO中,∠BAO+∠OBA=90°,
∴∠DAF=∠OBA,
在△OAB和△FDA中,
,
∴△OAB≌△FDA(AAS),
同理,△OAB≌△FDA≌△EBC,
∴AF=OB=EC=3,DF=OA=BE=1,
故D的坐标是(4,1),C的坐标是(3,4),
代入y=得:k=4,
则函数的解析式是:y=.
∴OE=4,
则C的纵坐标是4,
把x=3代入y=得:y=.即G的坐标是,
∴CG=4﹣=,
∴a=,
故选:A.
【点评】本题考查反比例函数与一次函数综合问题,全等三角形的判定和性质等,理解题意,综合运用这些知识点是解题关键.
14.如图,分别过反比例函数图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn),作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An﹣1Pn,再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3……,以此类推,则点B20的坐标是( )
A. B. C. D.
【分析】根据反比例函数图象上点的坐标特征求得点P1、P2的纵坐标,由平行四边形对边平行且相等的性质求得点B1的横坐标为2,纵坐标是y2+y1、B2的横坐标为3,纵坐标是y3+y2、B3的横坐标为4,纵坐标是y4+y3,据此可以推知点Bn的横坐标为n+1,纵坐标是:yn+1+yn=+=.
【解答】解:∵点P1(1,y1),P2(2,y2)在反比例函数图象上,
∴y1=4,y2=2;
∴P1A1=y1=4;
又∵四边形A1P1B1P2是平行四边形,
∴P1A1=B1P2=4,P1A1∥B1P2,
∴点B1的纵坐标是:y2+y1=+=6,即点B1的坐标是(2,6);
同理求得,点B2的纵坐标是:y3+y2=+=;即点B2的坐标是(3,);
点B3的纵坐标是:y4+y3=+=;
…
点Bn的横坐标为:xn=n+1,纵坐标是:yn+1+yn=+=;
∴点B20的坐标是(21,)
故选:D.
【点评】本题考查反比例函数图象上点的坐标特征、反比例函数的图象.解答此题的关键是根据平行四边形的对边平行且相等的性质求得点Bn的纵坐标yn+1+yn.
15.如图,在平面直角坐标系中,四边形OABC是矩形,且A(﹣6,0),S矩形OABC=24.反比例函数的图象与边AB,BC交于点D,E,连接DE,DC,则当△DCE的面积最大时,k的值为( )
A.﹣24 B.﹣12 C.﹣6 D.﹣4
【分析】根据图中的点的坐标表示出三角形的面积,得到关于k的二次函数,利用二次函数求出最值即可.
【解答】解:∵A(﹣6,0),S矩形OABC=24,
∴OA=6,
∴OC=4,
∴C(0,4),
∴D(﹣6,),E(,4),
∴CE=﹣,BD=4+,
∴S△DCE=CE BD= (﹣)(+4)=﹣k2﹣k=﹣(k+12)2+3,
∴当k=﹣12时,△ADE的面积最大.
故选:B.
【点评】本题考查了反比例函数函数图象上点的坐标特征,矩形的性质,表示出△DCE的面积是解本题的关键.
二.填空题(共25小题)
16.函数的图象上有两点P1(﹣1,y1),P2(﹣2,y2),若y1<y2,写出一个符合题意的k的值: 2(答案不唯一) .
【分析】根据反比例函数的增减性判断即可.
【解答】解:对于函数的图象上有两点P1(﹣1,y1),P2(﹣2,y2),
∵当﹣1>﹣2时,y1<y2,
∴反比例函数在每个象限内,y随x的增大而减小,
∴k>0,
∴符合题意的k值可以为大于0的任意数,
故答案为:2(答案不唯一).
【点评】本题考查反比例函数的图象与性质,熟知反比例函数的增减性是解答的关键.
17.若反比例函数y=(m+2)x|m|﹣5的图象在第一、三象限,则m的值为 2 .
【分析】根据反比例函数的图象与性质可得到关于m的不等式,解不等式即可求得m的取值范围.
【解答】解:∵反比例函数y=(m+2)x|m|﹣5的图象在第一、三象限,
∴|m|﹣5=﹣1,
解得:m=2 或m=﹣2,
∵m+2≠0,
∴m≠﹣2,
∴m=2.
故答案为:2.
【点评】本题考查了反比例函数的图象与性质,正确地求得m的值是解题的关键.
18.某商场销售一批散装坚果,进价为30元每斤,在销售时售货员发现坚果的日销量和每斤的利润正好成反比例关系,且价格调整为每斤50元时,当日销量为80斤,那么每日该坚果的销量y(单位:斤)与每斤价格x(单位:元)之间的函数表达式为 y= .
【分析】由题意知:坚果的日销量和每斤的利润正好成反比例关系,可设y=,把x=50,y=80代入求出k即可得到结果.
【解答】解:∵坚果的日销量和每斤的利润正好成反比例关系,
∴y与(x﹣30)成反比例关系,
设y=(k>0),
∵x=50时,y=80,
∴=80,
解得,k=1600,
∴y与x之间的函数表达式为:y=,
故答案为:y=.
【点评】本题考查了反比例函数的实际应用,根据题意先构造函数模型,利用待定系数法求出函数解析式是常用方法.
19.如图,反比例函数的图象与Rt△BOC的斜边OB交于点A,与边BC交于点D,若,且S△BOD=21,则k= 8 .
【分析】先设A点的坐标,然后利用求出点B的坐标,再求点D的坐标,从而得到CD和BD的长度,进而得到△COD和△BDO的面积比,最后求出△COD的面即,求出k的值.
【解答】解:设A(2a,),
∵=,
∴=,
∴B(5a,),
∵BC⊥x轴,点D在反比例函数的图象上,
∴D(5a,),S△COD=|k|,
∴CD=,BD=﹣=,
∴===,
∵S△BOD=21,
∴S△COD=4,
∴|k|=4,
∴k=8或k=﹣8(舍去),
故答案为:8.
【点评】本题考查了反比例函数的比例系数k的几何意义,反比函数的性质,解题的关键是通过设点A的坐标从而求得点C的坐标.
20.如图,直线y=kx(k<0)与双曲线交于 A(x1,y1)、B(x2,y2)两点,则2x1y2﹣5y2x1的值为 ﹣6 .
【分析】先根据A(x1,y1),B(x2,y2)双曲线y=﹣上的点可知x1y1=﹣2,x2y2=﹣2,再根据反比例函数与正比例函数均关于原点对称可知x1=﹣x2,y1=﹣y2,故可知x1y2=﹣x1y1,x2y1=﹣x2y2,把此关系式代入所求代数式求解即可.
【解答】解:∵A(x1,y1),B(x2,y2)双曲线y=﹣上的点,
∴x1y1=﹣2,x2y2=﹣2,
∵直线y=kx(k<0)与双曲线y=交于A(x1,y1),B(x2,y2)两点,
∴x1=﹣x2,y1=﹣y2,
∴x1y2=﹣x1y1,x2y1=﹣x2y2,
∴2x1y2﹣5x2y1=﹣2x1y1+5x2y2=(﹣2)×(﹣2)+5×(﹣2)=﹣6.
故答案为:﹣6.
【点评】本题考查的是反比例函数与一次函数的交点问题,根据题意得出x1y2=﹣x1y1,x2y1=﹣x2y2是解答此题的关键.
21.如图,在△AOB中,AO=AB,点B在x轴上,C、D分别为OA、OB的中点,连接CD,E为CD上任意一点,连接AE、BE,反比例函数的图象经过点A.若△ABE的面积为8,则k的值为 ﹣16 .
【分析】连接AD,则可得AD⊥OB,再由中位线定理得CD∥AB,从而可得△ABD的面积等于△ADO的面积,由反比例函数比例系数k的几何意义即可求得k的值.
【解答】解:如图,连接AD,
∵AO=AB,D为OB的中点,
∴AD⊥OB,S△ADO=S△ABD,
∵C、D分别为OA、OB的中点,
∴CD∥AB,
∴S△ADO=S△ABD=S△ABE=8,
由反比例函数比例系数k的几何意义得|k|=2S△ADO=16,
∵k>0,
∴k=﹣16.
故答案为:﹣16.
【点评】本题考查了等腰三角形的性质,三角形中位线定理,等底等高的三角形面积相等,反比例函数比例系数的几何意义等知识,连接AD,由中位线定理得到△ABE的面积转化为与之相等的△ADO的面积是解题的关键.
22.如图,在平面直角坐标系xOy中,直线y=x与反比例函数的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交x轴于点C,交反比例函数图象于点B,若,则b的值为 .
【分析】解析式联立,解方程求得A的横坐标,根据定义求得B的纵坐标,把纵坐标代入反比例函数的解析式求得B的坐标,代入y=x+b即可求得b的值.
【解答】解:∵直线y=x与反比例函数的图象交于点A,
∴联立,解得或,
∴A(1,1),
∴,
∵,
∴,
过B作BM⊥x轴于M,
∵将直线y=x沿y轴向上平移b个单位长度,交x轴于点C,
∴∠BCM=∠CBM=45°,
∴,
∴B的纵坐标为2,
把y=2代入得,,
∴,
∵将直线y=x沿y轴向上平移b个单位长度,得到直线y=x+b,
∴把代入y=x+b得,求得,
故答案为:.
【点评】本题是反比例函数与一次函数的交点问题,考查了反比例函数图象上点的坐标特征,一次函数的图象与几何变换,求得交点B的坐标是解题的关键.
23.如图, ABCD的顶点B,D在x轴上,AB⊥BD,反比例函数y=的图象经过点A,连接CA并延长交y轴于点E,连接DE,若△ADE的面积为2,则k的值为 4 .
【分析】假设AC,BD相交于点F,设点A的坐标为(a,),BF=m,由△ABF∽△EOF表示出OE,利用S△ADE=S△EFD﹣S△AFD=2即可求出结果.
【解答】解:如图,假设AC,BD相交于点F,设点A的坐标为(a,),BF=m,
∵四边形ABCD是平行四边形,AB⊥x轴,
∴DF=BF=m,OB=a,AB=,
∴OF=a+m,
∵AB∥OE,
∴△ABF∽△EOF,
∴,
∴,
∴EO=,
∵S△ADE=S△EFD﹣S△AFD=DF EO﹣DF AB=DF(EO﹣AB),
∴m()=2,
∴k=4,
故答案为:4.
【点评】本题考查了反比例函数中系数k的几何意义,点的坐标特征,平行四边形的性质,适当设出点的坐标,合理表示出三角形的面积是解题关键.
24.近视眼镜的镜片是凹透镜,研究发现,近视眼镜的度数y(度)与镜片焦距x(米)的关系近似满足,小宇原来佩戴400度近视眼镜,经过一段时间的矫正治疗,复查验光时,所配镜片焦距调整为0.4米,则小宇的眼镜度数 下降 (填“上涨”或“下降”)了 150 度.
【分析】根据眼镜的度数y(度)与镜片焦距x(m)的关系式满足,小宇原来佩戴400度近视眼镜,矫正治疗后所配镜片焦距调整为0.4m,可求出现在小宇佩戴的眼镜度数,两次比较,即可求解.
【解答】解:根据题意得,矫正治疗后所配镜片焦距调整为0.4m,
∴y=
∴y=250.
即矫正治疗后小宇佩戴的眼镜度数是250,小宇原来佩戴400度,
∴400﹣250=150,即下降了150度;
故答案为:下降;150.
【点评】本题主要考查反比例函数的实际运用,将矫正治疗后所配镜片焦距调整为0.4m代入反比例函数求出矫正后的度数,再与原来的度数比较是解题的关键.
25.某校科技小组进行野外考察,利用铺垫木板的方式通过了一片烂泥湿地,这是因为人和木板对湿地的压力F一定时,人和木板对地面的压强p(Pa)与木板面积S(m2)存在函数关系:(如图所示)若木板面积为0.2m2,则压强为 3000 Pa.
【分析】先利用待定系数法求出P关于S的函数解析式,再将S=0.2m2代入计算即可.
【解答】解:由已知反比例函数解析式为P=,
将(0.5,1200)代入,得:1200=,
解得:F=600,
∴P=,
当S=0.2m2时,P=,
解得P=3000,
∴当木板面积为0.2m2时,压强为3000Pa,
故答案为:3000.
【点评】本题主要考查反比例函数的应用,解题的关键是掌握待定系数法求反比例函数解析式.
26.如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,4),顶点C的坐标为(3,1),若反比例函数的图象与矩形ABCD有公共点,则k的值可以是 2(答案不唯一) .(写出一个即可)
【分析】根据矩形写出B,D两点坐标,然后利用双曲线经过点B,D时对应的k值,从而得到k的取值范围.
【解答】解:∵矩形ABCD的顶点A(1,4),C(3,1),
∴B(1,1),D(3,4),
当双曲线经过点B时,k的值最小,此时k=1×1=1,
当双曲线经过点D时,k的值最大,此时k=3×4=12,
∴k的取值范围为1≤k≤12.
∴k可以取2,
故答案为:2(答案不唯一).
【点评】本题考查反比例函数图象上点的坐标特征,熟记点的横纵坐标的积是定值k是解题的关键.
27.已知反比例函数的表达式为,A(x1,y1)和B(x2,y2)是反比例函数图象上两点,若x1<0<x2时,y1<y2,则m的取值范围是 m>﹣1 .
【分析】根据反比例函数的性质,可以得到关于m的不等式,从而可以求得m的取值范围.
【解答】解:∵反比例函数的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,
∴1+m>0,
解得m>﹣1,
故答案为:m>﹣1.
【点评】本题考查反比例函数图象上点的坐标特征,解答本题的关键是明确题意,利用反比例函数的性质解答.
28.小海利用杠杆平衡原理称药品质量(杠杆平衡时,动力×动力臂=阻力×阻力臂):如图1,小海发现天平平衡时左盘药品为m克,右盘砝码重20克;如图2,仍旧利用此杠杆,小海将砝码放在左盘,药品放在右盘,此时天平仍旧平衡,测得砝码重5克,右盘药品为n克.则m与n满足的关系式为 mn=100 .
【分析】根据“杠杆平衡时,动力×动力臂=阻力×阻力臂”,列出反比例函数的解析式即可.
【解答】解:根据“杠杆平衡时,动力×动力臂=阻力×阻力臂”,
由图1得m OA=20 OB,
∴m=,
由图2得5 OA=n OB,
∴n=,
∴mn=100,
故答案为:mn=100.
【点评】本题考查了反比例函数的应用,正确地求出反比例函数的解析式是解题的关键.
29.如图,一次函数y=ax+8与反比例函数的图象交于M(m,6)和N(n,2)两点,已知S△MON=8,则k= 6 .
【分析】过点M,N分别作x轴的垂线,垂足分别为Q,P,根据题意得出S△OMN=S梯形MNPQ=8,代入M,N的坐标得出n﹣m=2,将M,N代入一次函数,得出a=﹣2,进而求得点M(1,6),根据反比例函数的k的几何意义,即可求解.
【解答】解:如图所示,过点M,N分别作x轴的垂线,垂足分别为Q,P,
依题意,S△OMN+S△ONP=S△OMQ+S梯形MNPQ,
又∵S△ONP=S△OMQ,
∴S△OMN=S梯形MNPQ=8,
∵M(m,6)和N(n,2),
∴,
解得:n﹣m=2,
∵M(m,6)和N(n,2)在y=ax+8上,
∴6=am+8,2=an+8,
∴a(n﹣m)=﹣4,
∴a=﹣2,
∴m=1,
∴M(1,6),
∴k=6,
故答案为:6.
【点评】本题考查了反比例函数的k的几何意义,一次函数与反比例函数交点问题,熟练掌握反比例函数的k的几何意义是解题的关键.
30.如图,已知第一象限的双曲线与正方形OCAE的两边相交于D、B两点,直线过B点.则DE:AD的值是 .
【分析】设,则由正方形的性质得到OC=AC=AE=OE=a,设反比例函数的解析式是,利用待定系数法求出,再由点D的纵坐标是a,进而求出,则,由此即可得到答案.
【解答】解:∵直线经过B点,
∴设,
∵四边形OCAE是正方形,
∴OC=AC=AE=OE=a,
设反比例函数的解析式是,把代入,得,即.
∵在正方形OCAE中,点D在AE上,
∴点D的纵坐标是a,把y=a代入反比例函数的解析式,得,
解得,即,
∵,
∴.
故答案为:.
【点评】本题主要考查了反比例函数与一次函数综合,正方形的性质,正确求出是解题的关键.
31.如图,已知点M(1,2),N(4,n)(n>0),点P为线段MN上的一个动点,反比例函数(k为常数,x>0)的图象经过点P.
(1)当点P与点M重合时,k= 2 ;
(2)若点P与点N重合时,k=8,此时点Q(0,﹣9)到直线MN的距离为 11 .
【分析】(1)把M(1,2)代入计算即可;
(2)求出N点坐标,可得MN∥x轴,即可求出点Q到直线MN的距离.
【解答】解:(1)当点P与点M重合时,P点坐标为(1,2),代入,
得:
解得k=2;
(2)当点P与点N重合时,k=8,,
∴N点坐标为(4,2),
∵M(1,2),
∴MN∥x轴
∴点Q(0,﹣9)到直线MN的距离为:2﹣(﹣9)=11,
故答案为:2,11.
【点评】本题考查反比例函数的性质,将点的坐标代入解析式是解本题的关键.
32.如图,点A、D分别在函数图象上,点B、C在x轴上,若四边形ABCD为正方形,且点A在第二象限,则点A的坐标为 (﹣,3) .
【分析】利用反比例函数图象上点的坐标特征表示AB、BC、CD,再根据正方形的性质求出A坐标即可.
【解答】解:点A、D分别在函数图象上,
∵ABCD是正方形,
∴AB=BC=CD,
∵正方形ABCD的面积为:2+7=9.
∴AB=3,
∴OB=,
∴A的坐标为(﹣,3)
故答案为:(﹣,3).
【点评】本题考查反比例函数图象上点的坐标特征以及正方形的性质,理解反比例函数图象上点的坐标特征以及正方形的性质是正确解答的前提,设出点B,点C坐标,分别表示出正方形的边长是解决问题的关键.
33.已知反比例函数y=,当2≤x<5时,y的取值范围是 2<y≤5 .
【分析】求出x=2和x=5对应的y的值,再根据x的范围求出答案即可.
【解答】解:把x=2代入y=得:y=5,
把x=5代入y=得:y=2,
所以当2≤x<5时,y的取值范围是2<y≤5,
故答案为:2<y≤5.
【点评】本题考查了反比例函数图象上点的坐标特征和反比例函数的性质,能熟记反比例函数的性质是解此题的关键.
34. 如图,△ABC的顶点A在反比例函数 的图象上,顶点C在y轴上,AB∥y轴,若点B的坐标为(﹣2,2),S△ABC=4,则k的值为 ﹣12 .
【分析】利用S△ABC=4,求出AB,再利用点B的坐标求点A的坐标,即可求出k值.
【解答】解:∵B的坐标为(﹣2,2),
∴点B与y轴的距离为2,
∵S△ABC=4,
∴AB=4,
又∵B的坐标为(﹣2,2),
∴点B与x轴的距离为2,
∵AB∥y轴,
∴点A到x轴的距离为6,
∴点A坐标为(﹣2,6),
∴k=﹣2×6=﹣12.
故答案为:﹣12
【点评】本题考查了反比例函数的几何意义,解题的关键是三角形面积的求法.
35.如图,在平面直角坐标系中,反比例函数(k为常数,k≠0)的图象经过 ABCD的顶点B,AB交y轴于点E,AB∥x轴,F为CD边上一点,AE:CF:DF=1:2:3,连结FA并延长交x轴于点G,连结DG.
(1)设△ADF的面积S1,四边形ABCF的面积为S2,则S1:S2的值为 ;
(2)当△ADG的面积为3时,k的值为 8 .
【分析】(1)根据三角形和梯形的面积的同高的关系导出面积之比;
(2)根据同底三角形的面积之比等于高之比,同高三角形的面积之比等于底之比,求出△OBE的面积,再用反比例函数的几何意义求出k.
【解答】解:(1)设:每一份为a,
∵AE:CF:DF=1:2:3,
∴AE=a,CF=2a,DF=3a,
∵四边形ABCD是平行四边形,
∴AB=CD=5a,
设AB和CD之间的距离为h,
∴S1=,S2=(2a+5a) h=,
∴S1:S2==;
故答案为:.
(2)如图,设点D到GF的距离为h1,点B到AF的距离为h2,
连接BF、GE、GB、OB,
∵DF=3a,AB=5a,
∴S△ADF:S△ABF=3:5,即h1:h2=3:5,
∴S△AGD:S△AGB=3:5,
∵S△AGD=3,
∴S△AGB=5,
∵AE:BE=1:4,
∴S△BEG=4,
∴S△BEO=4,
∴=8,
∴k=±8.
∵反比例函数在一、三象限,
∴k=8.
故答案为:8.
【点评】本题考查了图形的面积之比的求法,要求学生有较强的识图能力.
36.如图,A,B为反比例函数第一象限图象上任意两点,连结BO并延长交反比例函数图象另一支于点C,连结AC交x轴于点F,交y轴于点G,连结BG,连结AB并向两侧延长分别交x轴于点E,交y轴于点D.已知,S△OBG=3,则= ,k的值为 .
【分析】如图,设A(a,),B(b,),过点A作AL⊥x轴于点L,AH⊥y轴于点H,过点B作BK⊥x轴于点K,BM⊥y轴于点M,过点C作CN⊥y轴于点N,连接OA,由BK∥AL,可得△EBK∽△EAL,推出:=,即=,再由AH∥BM,可得△DAH∽△DBM,推出=;再证得△BOM≌△CON(AAS),得出BM=CN,即可得==,由AH∥CN,可得△AGH∽△CGN,推出==,进而可得S梯形ABKO=S△AOB=,即k(﹣)=,再结合=,即可求得答案.
【解答】解:如图,设A(a,),B(b,),过点A作AL⊥x轴于点L,AH⊥y轴于点H,过点B作BK⊥x轴于点K,BM⊥y轴于点M,过点C作CN⊥y轴于点N,连接OA,
则AH=a,AL=,BM=b,BK=,
∵BK∥AL,
∴△EBK∽△EAL,
∴=,
∵=,
∴=,
∴=,
∴7BK=2AL,即7×=2×,
∴=,即=,
∵AH∥BM,
∴△DAH∽△DBM,
∴==,
∴=,
∴==,
∴DA=BE=AB,
∴DE=DA+AB+BE=AB,
∴=;
∵B、C关于原点O对称,
∴OB=OC,
∵S△OBG=3,
∴S△BCG=2S△OBG=6,
∵BM∥CN,
∴∠OBM=∠OCN,∠OMB=∠ONC,
∴△BOM≌△CON(AAS),
∴BM=CN,
∴==,
∵AH∥CN,
∴△AGH∽△CGN,
∴==,
∴==,
∴S△ABG=S△BCG=×6=,
∴S△ABC=S△ABG+S△BCG=+6=,
∴S△AOB=S△ABC=×=,
∵S△AOB+S△OBK=S△AOL+S梯形ABKO,S△OBK=S△AOL=k,
∴S梯形ABKO=S△AOB=,
∴(+)(b﹣a)=,
即k =,
∴k(﹣)=,
又∵=,
∴=,
∴k(﹣)=,
∴k=.
故答案为:,.
【点评】本题考查反比例函数的综合应用,反比例函数系数k的几何意义,中心对称性质,三角形面积,全等三角形的判定和性质,相似三角形的判定和性质等知识,本题综合性较强,难度较大,解题的关键是数形结合、方程思想等重要数学思想的应用.
37.如图,在平面直角坐标系中,放置一个等腰Rt△ABC纸片,∠A=90°,BC边与x轴重合,点A坐标为(3,2),若反比例函数与AB边交于点D,与AC边交于点E.
(1)当点D为AB中点时,反比例函数的表达式为 y= ;
(2)将如图放置的△ABC纸片的∠B沿过点D的直线翻折,当点B落到AC中点时,k= ;
(3)若双曲线与折线AD、AE所围成的区域内(含边界)有2个横纵坐标都是整数的点,则k的取值范围是 3<k<4 .
【分析】(1)作AF⊥BC于点F,求出BF=CF=AF=2,得到点B的坐标,利用中点坐标公式求出点D的坐标即可求解;
(2)求出点B′的坐标,求出直线AB的解析式,设D(m,m﹣1),利用勾股定理求出m的值,进而可求出k的值;
(3)数形结合,找出临界点求出k的值即可.
【解答】解:(1)作AF⊥BC于点F,
∵点A坐标为(3,2),OF=3,
∴AF=2,
∵△ABC是等腰直角三角形,AF⊥BC,
∴∠ABF=∠BAF=∠ACF=∠CAF=45°,
∴BF=CF=AF=2,
∴OB=3﹣2=1,OC=3+2=5,
∴B(1,0),
∴xD=,yD==1,
∴D(2,1),
∴k=2×1=2,
∴反比例函数的表达式为y=,
故答案为:y=;
(2)如图,点B落在AC上中点B′处,连接DB′.
由(1)可知,OC=5,
∴C(5,0),
∵点A坐标为(3,2),点B′是AC的中点,
∴B′(4,1),
设直线AB的解析式为y=kx+b,把点A和点B的坐标代入得,
解得,
∴直线AB的解析式为y=x﹣1,
设D(m,m﹣1),
∵BD=B′D,
∴(m﹣1)2+(m﹣1)2=(m﹣4)2+(m﹣1﹣1)2,
解得m=,
∴m﹣1=,
∴D(,),
∴k==.
故答案为:;
(3)∵点A坐标为(3,2),B′(4,1),
∴若双曲线与折线AD、AE所围成的区域内(含边界)有2个横纵坐标都是整数的点,则这两个点一定是点A和点B′,
把(3,1)代入y=得k=3,把(4,1)代入y=得k=4,
∴3<k≤4.
故答案为:3<k≤4.
【点评】本题是反比例函数的综合题,考查了反比例函数和一次函数的交点问题,待定系数法求函数解析式,等腰三角形的性质,以及勾股定理等知识,数形结合是解答本题的关键.
38.如图,点A,B分别在第一,二象限的反比例函数图象y=(k1>0),y=(k2<0)上,点C在y轴负半轴上,连结AB,OA,AC,且AC交x轴于点E.已知AB=2AC,CE=2AE,且∠AOC=135°.若AC⊥AB,且k1+k2=﹣,则k2的值为 ﹣ .
【分析】由∠AOC=135°,则∠AOy=45°,故设点A(m,m),由平行线分线段成比例求出点C(0,﹣2m),利用△BMA∽△ANC得到B的坐标,进而求解.
【解答】解:∵∠AOC=135°,则∠AOy=45°,
故设点A(m,m),
过点A作AT⊥y轴于点T,则OT=m,
∵OE∥AT,CE=2AE,即CE:AE=2,
∴OC:OT=2,故点C(0,﹣2m),
过点A作MN∥y轴交过点B与x轴的平行线于点M,交过点C与x轴的平行线于点N,
∵∠CAN+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠CAN=∠ABM,
∵∠BMA=∠ANC=90°,
∴△BMA∽△ANC,
∵AB=2AC,
则△BMA和△ANC的相似比为2:1,
即BM=2AN,AM=2CN,
设点B(s,t),
则m﹣s=2×(m+2m)且t﹣m=2m,
解得:s=﹣5m且t=3m,
则k2=st=﹣15m2,
而k1=m2,
∵k1+k2=﹣,
即﹣15m2+m2=﹣,
解得:m2=,
则k2=st=﹣15×=﹣,
故答案为:﹣.
【点评】本题考查的是反比例函数综合运用,涉及到一次函数和反比例函数的性质、平行线分线段正比例、三角形相似等,其中,正确设点A的坐标,用三角形相似确定点B坐标得方法,是此类题目解题的一半方法,题目综合性强,难度适中.
39.已知过原点的一条直线l与反比例函数的图象交于A,B两点(A在B的右侧).C是反比例函数图象上位于A点上方的一动点,连接AC并延长交y轴于点D,连接CB交y轴于点E.若AC=mCD,BC=nCE,则m﹣n= ﹣2 .
【分析】过点A作AF⊥y轴于点F,过点C作CM⊥y轴于M,过点B作BN⊥y轴于N,所以CM∥AF∥BN,AC=mCD,所以CM:AF:BN=1:(1+m):(1+m),可得CE:BE=1:(1+m),因为BC=nCE.所以CE:BE=1:(n﹣1),则1+m=n﹣1,整理即可得出结论.
【解答】解:根据题意作出图形,如图所示,
过点A作AF⊥y轴于点F,过点C作CM⊥y轴于M,过点B作BN⊥y轴于N,
∴CM∥AF∥BN,AC=mCD,
∴CM:AF:BN=1:(1+m):(1+m),
∴CE:BE=1:(1+m),
∵BC=nCE.
∴CE:BE=1:(n﹣1),
∴1+m=n﹣1,
∴m﹣n=﹣2.
故答案为:﹣2.
【点评】本题是反比例函数与一次函数的交点问题,考查了反比例函数的性质,反比例函数图象上点的坐标特征,平行线分线段成比例定理,能够正确表示出线段的比是解题的关键.
40.如图,在平面直角坐标系中,菱形OABC的边OC在x轴负半轴上,函数y=(x<0)的图象经过顶点A和对角线OB的中点M,作AN∥OB交y轴于点N,若△CMN的面积为6,则k的值为 16 .
【分析】如图,连接AM,延长BA交y轴于点F,点A,M,C三点共线.BF⊥y轴,设点M(m,n),则B(2m,2n),推出k=mn,推出A(,2n),再证明△AMN的面积=△AON的面积=6.可得 =6.整理得mn=16.
【解答】解:如图,连接AM,延长BA交y轴于点F,
∵点M是菱形对角线OB的中点,AB∥OC,
∴点A,M,C三点共线.BF⊥y轴,
设点M(m,n),则B(2m,2n),
∴k=mn,
∴A(,2n),
∴直线OB:y=x,
∵AN∥OB,
∴直线AN:y=x+.
∴N(0,n).
∴AF=,ON=.
∵点D是AC的中点,
∴△AMN的面积=△CMN的面积=6,
∵AN∥OB,
∴△AMN的面积=△AON的面积=6.
∴ =6.整理得mn=16.
∴k=16.
故答案为:16.
【点评】本题主要考查反比例函数与几何综合问题,涉及待定系数法求函数解析式,三角形的面积,菱形的性质等内容,关键是将△AMN的面积转化为△AON的面积.
三.解答题(共20小题)
41.已知反比例函数的图象经过点A(﹣4,﹣2).
(1)求反比例函数表达式;
(2)若点在该函数图象上,求m的值.
【分析】(1)将点A(﹣4,﹣2)代入求解即可;
(2)将点代入(1)求出的表达式中即可求出m的值.
【解答】解:(1)∵反比例函数的图象经过A(﹣4,﹣2),
∴将A(﹣4,﹣2)代入,得k=﹣4×(﹣2)=8,
∴反比例函数解析式为;
(2)∵点在这个函数图象上,
∴把代入
得,
解得:m=±4,
∴m的值为±4.
【点评】本题主要考查了反比例函数图象上点的性质,解题的关键是熟练掌握反比例函数图象上点的特征.
42.为了预防H1N1甲型流感,某校对教室采取喷洒药物消毒,在对某教室进行消毒的过程中,先经过5分钟的集中药物喷洒,再封闭教室10分钟,然后打开门窗进行通风,室内每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(分钟)之间的函数关系,在药物喷洒和封闭教室期间,y与x均满足一次函数的关系,在打开门窗通风后y与x满足反比例函数的关系,如图所示.
(1)研究表明,室内空气中的含药量低于3mg/m3时方可进入教室,从封闭教室开始,至少经过多少分钟后学生方可返回教室?
(2)当室内空气中的含药量不低于6mg/m3且特续时间不低于15分钟时,才能完全有效杀灭流感病毒.试通过分析判断此次消毒是否完全有效?
【分析】(1)当x≥15时,设y与x的函数关系式为:y=(m>o),代入图中点的坐标求出m,令y=3,求出时间x,再减去5分钟即可得结果.
(2)当0≤x≤5时,设y与x的函数关系式为:y=kx(k>0),代入图中点的坐标求出k,令y=6,求出x,对于y=,令y=6,求出时间x,用两时间之差与15作比较,即可得结果.
【解答】解:(1)当x≥15时,设y与x的函数关系式为:y=(m>o),
把(15,8)代入上式得,=8,
∴m=120,
∴y=,
当y=3时,=3,
∴x=40,
40﹣5=35(分钟).
答:至少经过35分钟后学生方可返回教室.
(2)当0≤x≤5时,设y与x的函数关系式为:y=kx(k>0),
把(5,10)代入上式得,5k=10,
∴k=2,
∴y=2x,
当y=6时,2x=6,
∴x=3,
对于y=,当y=6时,=6,
∴x=20,
∵20﹣3=17>15,
∴此次消毒是完全有效,
答:此次消毒完全有效.
【点评】本题考查了反比例函数与一次函数的实际应用,是一个分段函数,涉及待定系数法等知识点.掌握自变量、函数值等知识是解题的关键.
43.如图是某型号冷柜循环制冷过程中温度变化的部分示意图.该冷柜的工作过程是:当冷柜温度达到﹣4℃时制冷开始,温度开始逐渐下降,当温度下降到﹣20℃时制冷停止,温度开始逐渐上升,当温度上升到﹣4℃时,制冷再次开始,…,按照以上方式循环工作.通过分析发现,当0≤x<4时,温度y是时间x的一次函数;当4≤x<t时,温度y是时间的反比例函数.
(1)求t的值;
(2)当前冷柜的温度﹣10℃,经过多长时间温度下降到﹣20℃?
【分析】(1)由函数图象可知当时间为t时,温度与时间之间是反比例函数关系,由图象上(4,﹣20)点求出反比例函数的关系式,再由反比例函数关系式求出当y=﹣4时的t的值即可;
(2)分别求得x=﹣10时的函数值,分类讨论即可求解.
【解答】解:(1)设反比例函数的关系式为.
把(4,﹣20)代入,得:.
∴k=﹣80.
∴.
当y=﹣4时,,
∴t=20.
(2)设一次函数函数的关系式为y=kx﹣4.
把(4,﹣20)代入,得:﹣20=4k﹣4,解得:k=﹣4,
∴y=﹣4x﹣4,
当在温度下降过程中,﹣10=﹣4x﹣4,x=1.5,
∴4﹣1.5=2.5(min)
此时,经过2.5分钟温度可下降到﹣20°C.
当在温度上升过程中时,x=8,
∴20﹣8+4=16(min).
此时,在经过16分钟温度可降至﹣20°C.
【点评】本题考查了一次函数与反比例函数的综合运用,熟练掌握反比例函数的性质是解题的关键.
44.如图在平面直角坐标系中,一次函数y=kx+b的图象经过点A(0,﹣4)、B(2,0)交反比例函数的图象于点C(3,a),点P在反比例函数的图象上,横坐标为n(0<n<3),PQ∥y轴交直线AB于点Q,连接OP、OQ.
(1)求一次函数和反比例函数的表达式;
(2)求△OPQ面积的最大值.
【分析】(1)由A(0,﹣4)、B(2,0)的坐标可求出一次函数的关系式,进而求出点C的坐标,代入,求得反比例函数解析式;
(2)设点,点Q(n,2n﹣4),得出关于PQ与n的关系式,进而根据三角形面积公式求解,根据二次函数的性质即可求得最大值.
【解答】解:(1)把A(0,﹣4)、B(2,0)代入一次函数y=kx+b得:
,
解得:,
∴一次函数的关系式为y=2x﹣4,
将点C(3,a)代入y=2x﹣4,得a=2×3﹣4=2,
∴点C(3,2),
将点C(3,2)代入,
得出m=3×2=6,
∴;
(2)∵点P在反比例函数的图象上,点Q在一次函数的图象上,0<n<3,
设点,点Q(n,2n﹣4),
∴,
∴,
∵﹣1<0,
∴当n=1时,,
所以,△OPQ面积的最大值是4.
【点评】本题考查反比例函数、一次函数的解析式,将面积用函数的数学模型表示出来,利用函数的最值求解是解决问题的基本思路.
45.在平面直角坐标系xOy中,直线y1=﹣2x+1与反比例函数图象的一个交点为点M.
(1)当点M的坐标为(2,m)时,求k的值;
(2)当x<﹣1时,对于x的每一个值,都有y1>y2,求k的取值范围.
【分析】(1)将点M代入y1=﹣2x+1,求出m的值,再将点M坐标代入反比例函数解析式求k的值即可;
(2)根据反比例函数图象上点的坐标特征,分情况讨论:①当k>0时,②当k<0时,分别求解即可.
【解答】解:(1)将点M(2,m)代入y1=﹣2x+1,
得﹣4+1=m,
∴m=﹣3,
∴点M坐标为(2,﹣3),
∴k=2×(﹣3)=﹣6;
(2)如图所示:
①当k>0时,当x<﹣1时,对于x的每一个值,都有y1>y2,
②当k<0时,x=﹣1时,﹣2×(﹣1)+1≥﹣k,
解得﹣3≤k<0,
综上所述,满足条件的k的取值范围是﹣3≤k<0或k>0.
【点评】本题考查了反比例函数与一次函数的交点问题,熟练掌握反比例函数图象上点的坐标特征是解题的关键.
46.如图,已知正比例函数y1=x的图象与反比例函数y2=的图象相交于点A(3,n)和点 B.
(1)求n和k的值;
(2)请结合函数图象,直接写出不等式x﹣<0的解集;
(3)如图,以AO为边作菱形AOCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE、OE,求△AOE的面积.
【分析】(1)先把点A(3,n)代入正比例函数解析式求出n的值,再把求出的点A坐标代入反比例函数解析式即可求出k值;
(2)根据正比例函数和反比例函数都是关于原点成中心对称的,可得出点B的坐标,然后根据图象即可写出解集;
(3)根据题意作出辅助线,然后求出OA的长,根据菱形的性质求出OC的长,可推出,然后求出菱形的面积即可求出△AOE的面积.
【解答】解:(1)把点A(3,n)代入正比例函数可得:n=4,
∴点A(3,4),
把点A(3,4)代入反比例函数,
可得:k=12;
(2)∵点A与点B是关于原点对称的,
∴点B(﹣3,﹣4),
∴根据图象可得,不等式x﹣<0的解集为:x<﹣3或0<x<3;
(3)如图所示,过点A作AG⊥x轴,垂足为G,
∵A(3,4),
∴OG=3,AG=4
在Rt△AOG中,AO==5
∵四边形AOCD是菱形,
∴OC=OA=5,,
∴.
【点评】本题主要考查的是反比例函数的综合题型,解题关键:一是求出反比例函数解析式,二是求出菱形的面积.
47.已知直线y1=k1x+b与双曲线相交于点P(﹣2,1)、Q(1,m).
(1)求k1,b,k2的值;
(2)在同一坐标系中画出直线y1=k1x+b与双曲线,根据图写出不等式k1x+b的解集.
【分析】(1)利用待定系数法即可求得;
(2)作出函数的图象,根据图象即可求得.
【解答】解:(1)∵双曲线经过点P(﹣2,1)、Q(1,m),
∴k2=﹣2×1=1×m,
∴k2=﹣2,m=﹣2,
∴y2=﹣,Q(1,﹣2),
∵直线y1=k1x+b过点P(﹣2,1)、Q(1,﹣2),
∴,
解得
故k1,b,k2的值分别为﹣1,﹣1,﹣2;
(2)如图:
由图象可知,不等式k1x+b的解集为x≤﹣2或0<x≤1.
【点评】本题考查了反比例函数与一次函数的交点、待定系数法求函数的解析式、函数与不等式的关系,熟练掌握待定系数法以及数形结合思想的运用是解题的关键.
48.已知反比例函数(k为常数,k≠0)与正比例函数y2=x的图象有一个交点为P(3,m).
(1)求k的值;
(2)将点P向下平移6个单位,再向左平移5个单位后,得点P′,试判断点P′是否在函数y1的图象上,并说明理由;
(3)当y1>y2时,利用函数图象直接写出自变量x的取值范围.
【分析】(1)由正比例函数的解析式求得点P的坐标,代入数(k为常数,k≠0)即可求得k的值;
(2)求得P′的坐标为(﹣2,﹣3),由﹣2×(﹣3)=6≠k,即可判断点P′不在函数y1的图象上;
(3)利用图象即可求解.
【解答】解:(1)∵正比例函数y2=x的图象过交点为P(3,m),
∴m=3,
∴P(3,3),
∵点P在反比例函数(k为常数,k≠0)的图象上,
∴k=3×3=9;
(2)将点P向下平移6个单位,再向左平移5个单位后,得点P′(﹣2,﹣3),
∵﹣2×(﹣3)=6≠9,
∴点P′不在函数y1的图象上;
(3)由图象可知,当y1>y2时,自变量x的取值范围是x<﹣3或0<x<3.
【点评】本题是反比例函数于一次函数的交点问题,考查了一次函数图象上点的坐标特征,待定系数法求反比例函数的解析式,函数与不等式的关系,数形结合是解题的关键.
49.如图,已知点A(1,4),B(7,1),点P作线段AB上,并且点P的横、纵坐标均为整数.经过点P的双曲线为.
(1)当点P与点B重合时,求L的表达式;
(2)求线段AB所在直线的函数表达式;
(8)直接写出k的最小值和最大值.
【分析】(1)利用待定系数法即可求解;
(2)根据待定系数法求得即可;
(3)根据题意点P的坐标为(1,4)或(3,3)或(5,2)或(7,1),根据图象上点的坐标特征k=xy即可求得k的最小值和最大值.
【解答】解:(1)∵点A(1,4),B(7,1),点P与点B重合,
∴P(7,1),
∵双曲线经过点P,
∴k=7×1=7,
∴L的表达式为y=;
(2)设直线AB的解析式为y=ax+b,
∴,
解得,
∴线段AB所在直线的函数表达式为y=﹣+;
(3)∵点A(1,4),B(7,1),点P在线段AB上,
∴点P坐标为(1,4)或(3,3)或(5,2)或(7,1),
∵经过点P的双曲线为,
∴k的最小值为4,最大值为10.
【点评】本题考查了待定系数法求反比例函数和一次函数的解析式,反比例函数图象上点的坐标特征,熟知反比例函数图象上点的坐标特征是解题的关键.
50.如图,一次函数y=kx+b(k≠0)与反比例函数的图象交于点A(3,4),B(a,﹣2).
(1)求一次函数和反比例函数的解析式;
(2)求不等式的解集;
(3)连接BO并延长,交反比例函数图象于点C,连接AC,求△ABC的面积.
【分析】(1)待定系数法求出一次函数和反比例函数解析式;
(2)通过图象找到所要求的解集区域,再通过交点坐标得出解集;
(3)作水平辅助线把图象分割成两个三角形,再求面积.
【解答】解:(1)反比例函数 (m≠0)的图象双曲线过点A(3,4),
∴m=xy=3×4=12,
∴,
∵双曲线过点B(a,﹣2),
∴﹣2a=12,
∴a=﹣6,
∴点B(﹣6,﹣2),
∵一次函数y=kx+b的图象直线过点A(3,4),B(﹣6,﹣2),
则有
∴,
∴;
(2)由图可知,当﹣6<x<0或x>3时,一次函数的图象在反比例函数的图象上方,
故不等式的解集是:﹣6<x<0或x>3;
(3)如解图,设AB与y轴的交点为D,连接CD.
当x=0时,.
∴D(0,2).
∵反比例函数和正比例函数的图象(直线BC)都关于原点中心对称,
∴这两个函数图象的交点关于原点中心对称,
∵B(﹣6,﹣2).
∴C(6,2),
∴点C和点D的纵坐标相等,
∴CD∥x轴.
∴CD=6.
分别记点A,B,D的纵坐标为yA,yB,yD,
∴ ,
,
∴S△ABC=S△ACD+S△BCD=6+12=18.
【点评】本题考查待定系数法求解析式、一次函数与反比例函数图象的交点、围成的图形面积,掌握反比例函数的图象和性质是本题关键.
51.如图,在平面直角坐标系中,反比例函数y=(x>0)与一次函数y=ax+b(a≠0)的图象相交于点A(2,m)与点B(4,2).
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上是否存在一点P,使得AP+BP最小,若存在,求出点P坐标;若不存在,请说明理由.
【分析】(1)把B点的坐标代入反例函数解析式即可求出反比例函数解析式,进而得出A的坐标,把A、B的坐标代入一次函数解析式即可求出一次函数解析式;
(2)△AOB的面积=△BOD的面积﹣△AOD的面积;
(3)首先求得点B关于x轴的对称点的坐标,然后求得直线AB′的解析式后求得其与x轴的交点即可求得点P的坐标.
【解答】解:(1)∵反比例函数y=(x>0)的图象经过B(4,2),
∴k=4×2=8,
∴反比例函数的表达式为y=,
∵点A(2,m)在y=上,
∴m=4,
∴A点坐标为(2,4);
把A,B两点的坐标代入y=ax+b,得,
解得,
∴一次函数的表达式为:y=﹣x+6;
(2)当x=0时,y=﹣x+6=6,
∴D点坐标为(0,6),
∴S△AOB=S△BOD﹣S△AOD==6,
即△AOB的面积为6;
(3)在x轴上存在点P,使得AP+PB最小.
作点B(4,2)关于x轴的对称点B′(4,﹣2),如图,连接AB′.
设直线AB'的解析式为:y=a′x+b′,
∴,
解得,
∴直线AB'的解析式为:y=﹣3x+10,
令y=0,解得x=,
∴P(,0)可使AP+BP最小.
【点评】本题主要考查了反比例函数和一次函数的交点问题,轴对称﹣最短路线问题.正确运用待定系数法求反比例函数和一次函数的解析式是解题的关键.
52.在平面直角坐标系中,已知一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,且与反比例函数的图象在第一象限内交于P,K两点,连接OP,△OAP的面积为.
(1)求一次函数与反比例函数的解析式;
(2)若C为线段OA上的一个动点,当PC+KC最小时,求△PKC的面积.
【分析】(1)根据待定系数法可求出直线AB的解析式,根据△OAP的面积可得出点P的坐标,代入反比例函数解析式可得出反比例函数的解析式;
(2)作点P关于x轴的对称点P′,连接KP′,线段KP′与x轴的交点即为点C,求出直线KP′的解析式,令y=0,可得出点C的坐标,再根据三角形的面积公式可得出结论.
【解答】解:(1)∵一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,
∴,
解得.
∴一次函数的解析式为:y1=﹣x+,
∵△OAP的面积为.
∴ OA yP=,
∴yP=,
∵点P在一次函数图象上,
∴令﹣x+=,
解得x=4,
∴P(4,).
∵点P在反比例函数的图象上,
∴k2=4×=2.
∴反比例函数的解析式为:y2=;
(2)令﹣x+=,解得x=1或x=4,
∴K(1,2),
作点P关于x轴的对称点P′,连接KP′,线段KP′与x轴的交点即为点C,
∵P(4,).
∴P′(4,﹣).
∴PP′=1,
∴直线KP′的解析式为:y=﹣x+.
令y=0,解得x=.
∴C(,0).
∴S△PKC= (xC﹣xK) PP′
=×(﹣1)×1
=.
∴当PC+KC最小时,△PKC的面积为.
【点评】本题是反比例函数与一次函数的交点问题,主要考查待定系数法求函数解析式,数形结合思想,轴对称最值问题,三角形的面积问题等知识,关键是求出一次函数和反比例函数的解析式.
53.如图,在Rt△ABC中,AC=8,BC=4,AC⊥x轴,垂足为C,AB边与y轴交于点D,反比例函数的图象经过点A.
(1)若点D是AB边的中点,求直线AB和反比例函数的表达式.
(2)将AB边沿AC边所在直线翻折,交反比例函数的图象于点E,交x轴于点F,若点E的纵坐标为2,求k的值.
【分析】(1)根据题意求得A(2,8),B(﹣2,0),然后利用待定系数法即可求得线AB和反比例函数的表达式;
(2)作EH⊥x轴于H,由题意可知CF=BC=4,利用平行线分线段成比例定理得出FH=1,即可求得CH=3,设A(x,8),则E(x+3,2),代入反比例函数解析式得到k=8x=2(x+3),即可求得k=8.
【解答】解:(1)在Rt△ABC中,AC=8,BC=4,AC⊥x轴,垂足为C,
∴AC∥OD,
∵点D是AB边的中点,
∴O为BC的中点,
∴A(2,8),B(﹣2,0),
设直线AB为y=ax+b,
∴,
解得,
∴直线AB为y=2x+4,
∵反比例函数的图象经过点A,
∴k=2×8=16,
∴反比例函数的表达式为y=;
(2)作EH⊥x轴于H,
由题意可知CF=BC=4,
∵点E的纵坐标为2,
∴EH=2,
∵EH∥AC,
∴,即,
∴FH=1,
∴CH=4﹣1=3,
设A(x,8),则E(x+3,2),
∵反比例函数的图象过点A、E,
∴k=8x=2(x+3),
∴x=1,
∴k=8x=8.
【点评】本题是反比例函数与一次函数图象的交点问题,考查了待定系数法求函数的解析式,平行线分线段成比例定理,求得交点坐标是解决问题的关键.
54.如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=的图象交于A、B两点,已知点A的坐标是(﹣2,m+3),点B的坐标是(4,m).
(1)求反比例函数与一次函数的表达式;
(2)求△AOB的面积;
(3)当kx+b>时,x的取值范围是 x<﹣2或0<x<4 .
【分析】(1)根据反比例函数y=的图象经过点A(﹣2,m+3),B(4,m),求出m,n的值,得出反比例函数的解析式,从而求出点A、B的坐标,再根据一次函数y=kx+b的图象经过点A和点B,求出k和b的值,得出一次函数的解析式;
(2)根据三角形的面积公式可得答案;
(3)根据函数的图象和交点坐标即可求得.
【解答】解:(1)∵反比例函数y=的图象经过点A(﹣2,m+3),B(4,m),
∴n=﹣2(m+3)=4m,
∴m=﹣1,
∴A(﹣2,2),B(4,﹣1),n=4m=﹣4,
∴反比例函数的解析式为y=﹣,
∵一次函数y=kx+b的图象经过点A,B,
∴,
解得,
故一次函数的解析式为y=﹣x+1;
(2)令x=0,则y=﹣x+1=1,
∴M(0,1),
∴△AOB的面积=S△BOM+S△AOM==3;
(3)观察图象,当kx+b>时,x的取值范围是:x<﹣2或0<x<4.
故答案为:x<﹣2或0<x<4.
【点评】此题考查了反比例函数和一次函数的交点问题,解题的关键是根据所给的条件得出A、B点的坐标,求出函数的解析式.注意运用数形结合的思想,难度不大,是中考常考的题型.
55.如图,一次函数y=﹣2x+1与反比例函数的图象在第二象限交于点A,且点A的横坐标为﹣1.
(1)求反比例函数的解析式;
(2)点B的坐标是(﹣2,0),若点P在y轴上,且△AOP的面积与△AOB的面积相等,求点P的坐标.
【分析】(1)首先确定点A的坐标,再利用待定系数法求出k即可;
(2)设P(0,m),构建方程求解.
【解答】解(1)∵一次函数y=﹣2x+1与反比例函数y=的图象在第二象限交于点A,点A的横坐标为﹣1,
当x=﹣1时,y=﹣2×(﹣1)+1=3,
∴A(﹣1,3),
∴3=,
∴k=﹣3,
∴反比例函数的解析式为y=﹣;
(2)设P(0,m),
∵△AOP的面积与△AOB的面积相等,
∴×|m|×1=×2×3,
∴m=±6,
∴P(0,6)或(0,﹣6).
【点评】本题考查反比例函数的性质,一次函数的性质等知识,解题的关键是掌握待定系数法,属于中考常考题型.
56.如图1,有一块边角料ABCDE,其中AB,BC,DE,EA是线段,曲线CD可以看成反比例函数图象的一部分.小宁想利用这块边角料截取一个面积最大的矩形MNQP,其中M,N在AE上(点M在点N左侧),点P在线段BC上,点Q在曲线CD上.测量发现:∠A=∠E=90°,AE=5,AB=DE=1,点C到AB,AE所在直线的距离分别为2,4.
(1)小宁尝试建立坐标系来解决该问题,通过思考,他把A,B,C,D,E这5个点先描到平面直角坐标系上,记点A的坐标为(﹣1,0);点B的坐标为(﹣1,1).
请你在图2中补全平面直角坐标系并画出图形ABCDE;
(2)求直线BC,曲线CD的解析式;
(3)求矩形MNQP的最大面积.
【分析】(1)由题意即可如图;
(2)用待定系数法即可求解;
(3)设点P坐标为,得到点Q坐标为,进而求解.
【解答】解:(1)由题意,如图如下:
(2)设直线BC的解析式为y=kx+b(k≠0),
则,解得:,
则直线BC的解析式为:,
设曲线的表达式为:y=,
由点C(1,4)得曲线CD的解析式得:m=4×1=4,
则反比例函数的表达式为:;
(3)如图,设点M的横坐标为m,则点P坐标为,
∴.
∵四边形MNQP是矩形,
∴,
∴点Q坐标为,
设矩形MNQP的面积为S.
则,
∴当时,矩形MNQP的面积的最大值为.
【点评】本题为反比例函数综合题,涉及到一次函数的基本性质、矩形的性质、图形的面积等,有一定的综合性,难度不大.
57.如图,在平面直角坐标系xOy中,直线l:y=x+b与x轴、y轴分别交于点A、B,与双曲线H:y=交于点P(2,),直线x=m分别与直线l和双曲线H交于点E、D.
(1)求k和b的值;
(2)当点E在线段AB上时,如果ED=BO,求m的值;
(3)如果△BDE是以BE为腰的等腰三角形,求点E的坐标.
【分析】(1)利用待定系数法求出k和b的值即可;
(2)由题意得出,E(m,m+3),D(m,),DE=m+3﹣,利用DE=BO,建立方程求解即可;
(3)过点E作EF⊥y轴于点F,运用勾股定理求出BE=|m|,再根据BE=DE列方程求解,根据m的值确定E点的坐标即可.
【解答】解:(1)把点P(2,)代入y=,
得=,
解得k=9,
把点P(2,)代入y=x+b,
得+b=,
解得b=3;
(2)在直线y=x+3中,令x=0,
得y=3,
∴B(0,3),
∴OB=3,
令y=0,得x+3=0,
解得x=﹣4,
∴A(﹣4,0),
∵直线x=m,分别与直线l和双曲线H交于点E、D,
∴E(m,m+3),D(m,),
∵点E在线段AB上,
∴﹣4≤m≤0,
∴ED=m+3﹣,
∵ED=BO,
∴m+3﹣=3,
解得m=﹣2,m'=2(不符合题意,舍去),
∴m的值为﹣2;
(3)如图,过点E作EF⊥y轴于点F,
∵B(0,3),E(m,m+3),D(m,),
∴F(0,m+3),
∴BE====|m|,
又∵DE=|m+3﹣|,△BDE是以BE为腰的等腰三角形,
∴BE=DE,
即|m|=|m+3﹣|,
解得m=﹣3,m'=,
∴E(﹣3,)或(,).
【点评】本题主要考查反比例函数的综合题,熟练掌握反比例函数的图象和性质,一次函数的图形和性质,待定系数法求解析式等知识是解题的关键.
58.如图,已知直线y=x﹣2与x轴交于A点,与y轴交于B点,P(m,n)为双曲线上一动点,过P点分别作x轴,y轴的垂线,垂足分别为C,D,射线PC交直线AB于点E,射线PD交直线AB于点F.
(1)当DF=PC时,求m的值;
(2)连接OE,OF,求证:∠EOF的度数为45°;
(3)在双曲线上有一点Q(不与点P重合),连接PQ,有PQ∥AB,将线段PQ沿直线AB翻折得到线段P′Q′.若线段P′Q′与坐标轴没有交点,求此时n的取值范围.
【分析】(1)由题意得:点P(m,﹣),则点F(2﹣,﹣),得到=2﹣,即可求解;
(2)证明△OFA∽△EFO,得到∠FOE=∠FAO,即可求解;
(3)设点P′、Q′恰好坐落在x、y轴上,此时,线段P′Q′与坐标轴有交点的临界点,进而求解.
【解答】(1)解:由题意得:点P(m,﹣),则点F(2﹣,﹣),
∵DF=PC,即=2﹣,
解得:m=2;
(2)证明:∵点E、F在直线AB上,故设点E、F的坐标分别为:(m,m﹣2)、(n+2,n),
由点O、E、F的坐标得:OF2=(n+2)2+n2=2n2+4n+4,
EF==(m﹣n﹣2),AF==n,
则EF AF=(m﹣n﹣2)×n=2n2+4n+4=OF2,
∵∠OFA=∠EFO,
∴△OFA∽△EFO,
∴∠FOE=∠FAO,
由直线AB的表达式知,∠FAO=45°,
∴∠EOF的度数为45°;
(3)解:如图,设点P′、Q′恰好坐落在x、y轴上,此时,线段P′Q′与坐标轴有交点的临界点,
连接AP、BQ,
由图象的对称性知,PP′⊥AB,
则点A在PP′的中垂线上,即PA=PA′,
由AB的表达式知,∠BAP′=45°=∠BAP,
则∠PAP′=90°,则点P的横坐标为2,则点P(2,﹣1),
同理可得,点Q(1,﹣2),
此外,当n=﹣时,点P、Q重合,不符合题意,
则﹣2<n<﹣1且n≠﹣.
【点评】本题为反比例函数综合题,考查了反比例函数与一次函数的交点问题、三角形相似、勾股定理的运用等,有一定的综合性,难度适中.
59.一次函数y=﹣2x+6与反比例函数(k>0,k为常数)的图象交点为A(a,4)和点B,点C是反比例函数(k>0,k为常数)在第三象限内的图象上一点.
(1)求反比例函数的解析式和点B的坐标;
(2)若点C为直线OB与反比例函数的另一个交点,求△ACB的面积;
(3)我们将对角线相等且互相垂直的四边形称为“等直四边形”.如图2,在平面内一点D,AB∥CD,且四边形ABCD为“等直四边形”,求点C的坐标.
【分析】(1)用待定系数法即可求解;
(2)由△ACB的面积=S△ATC+S△ATB=AT (xB﹣xC),即可求解;
(3)证明△HGA≌△BNH(AAS),得到GA=HN,GH=BN,进而求解.
【解答】解:(1)将点A的坐标代入一次函数表达式得:4=﹣2a+6,则a=1,即点A(1,4),
将点A的坐标代入反比例函数表达式得:k=1×4=4,
则反比例函数的表达式为:y=①,
联立,
解得:,
即点B(2,2);
(2)根据点的对称性,点C和点B关于原点对称,则点C(﹣2,﹣2),
由题意得,直线BC的表达式为:y=x,
过点A作AT∥y轴于点T,则点T(1, 1),则AT=4﹣1=3,
则△ACB的面积=S△ATC+S△ATB=AT (xB﹣xC)=×(2+2)=6;
(3)设AC和BD交于点H,
根据“等直四边形”的定义,AC⊥BD,则∠AHB=90°,且AC=BD,
根据图象的对称性,△ABH为等腰直角三角形,且AH=BH,
如图,将左侧图部分放大,设点H(m,n),
过点H作GN∥y轴,交过点A和x轴的平行线于点G,交过点B与x轴的平行线于点N,
∵∠GHA+∠GAH=90°,∠GHA+∠BHN=90°,
∴∠GAH=∠BHN,
∵∠HGA=∠BNH=90°,AH=BH,
∴△HGA≌△BNH(AAS),
则GA=HN,GH=BN,
即n﹣2=1﹣m且4﹣n=2﹣m,
解得:,
则点H(,),
由点A、H的坐标得,直线AH的表达式为:y=3x+1②,
联立①②得:=3x+1,
解得:x=1(舍去)或﹣,
即点C(﹣,﹣3).
【点评】本题为反比例函数综合运用题,涉及到新定义、面积的计算、一次函数的性质等,正确理解新定义是本题解题的关键.
60.一、问题背景:
数学活动课上,老师拿出一个由五连格边长为1的正方形连成的L形教具,将它放入一个的直角三角形中,
∠BCA=90°,∠B=30°,如图1顶点D,E,F,G刚好落在三边上,请求出此直角三角形的面积.
二、问题提出与解决:(以下问题二选一解答)
(1)小颖同学受到启发,将此教具放入如图的直角坐标系中,顶点A,B,C分别落在坐标轴上,提出问题:如图2,如果反比例函数图象经过顶点D,试求出反比例解析式.
(2)小明同学也受到启发,画了一个圆,如图3,将此教具放入圆内,使圆经过其顶点A,B,C,提出问题:怎么算出圆的面积?
【分析】(一)如图1,由题意知GD=2,GF=4,GF∥AB,∠B=30°,则∠CFG=∠B=30°,求出AG,AC,BC的值,再根据直角三角形的面积公式计算即可;
(二)(1)如图2,过D作DE⊥x轴于E,由题意知,AB=1,AD=4,CF=1,BF=3,∠DAB=∠ABF=∠CFB=∠AOB=∠DEA=90°,然后由△BAO∽△CBF和△ADE∽△BAO求出AO,BO,AE,DE,从而得出D坐标,代入反比例函数解析式求k,进而可得反比例函数解析式;
(2)如图3,取AB中点E,作EF⊥FC,取圆心O,连接OB,OC,则OB=OC,由正方形的性质CF=,BE=,EF=4,设OF=x,OE=4﹣x,在Rt△COF和Rt△BOE中,由勾股定理得关于x的方程,解方程求x的值,OC的值,进而可得⊙O的半径,然后代入圆的面积公式进行求解即可.
【解答】解:一、问题背景:
如图所示:
由题意知GD=2,GF=4,GF∥AB,∠B=30°,
∴∠CFG=∠B=30°,∠A=60°,
∴CG=GF=2,AG==,
∴AC=+2,BC=AC tan60°=4+2,
∴S△ABC=AC BC=×(+2)×(4+2)=+8,
∴此直角三角形的面积为+8;
二、问题提出与解决:
(1)如图所示:过D作DE⊥x轴于E,
由题意知,AB=1.AD=4,CF=1,BF=3,∠DAB=∠ABF=∠CFB=∠AOB=∠DEA=90°,
在Rt△BCF中,由勾股定理得BC==,
∵∠ABO+∠BAO=∠ABO+∠CBF,
∴∠BAO=∠CBF,
∴△BAO∽△CBF,
∴,即,
解得AO=,BO=,
同理△ADE∽△BAO,
∴,
即==,
解得AE=,DE=,
∴OE=AO+AE=,
∴D(﹣,),
∴k=xy=﹣×=﹣,
∴反比例函数解析式为y=﹣;
(2)如图,取AB中点E,作EF⊥FC,取圆心O,连接OB,OC,则OB=OC,
由正方形的性质CF=,BE=,EF=4,
设OF=x,OE=4﹣x,
在Rt△COF中,由勾股定理得:OC2=CF2+OF2=()2+x2,
在Rt△BOE中,由勾股定理得:OB2=BE2+OE2=()2+(4﹣x)2,
∴()2+x2=()2+(4﹣x)2,
解得x=,
∴OC=,
∴⊙O的半径为,
∴圆O的面积=πr2=π×()2=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第6章反比例函数好题精选60题
一.选择题(共15小题)
1.已知反比例函数的图象经过点(2,3),则下列描述正确的是( )
A.y的值随x值的增大而减小
B.图象位于第二、四象限
C.当x>0时,y<0
D.点(3,2)在图象上
2.若点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数的图象上,若x1<x2<0<x3则y1,y2,y3的大小关系是( )
A.y2<y1<y3 B.y3<y2<y1 C.y1<y2<y3 D.y3<y1<y2
3.如图,点A(m,m+1),B(m+3,m﹣1)都在反比例函数的图象上,则k的值为( )
A.3 B.6 C.14 D.12
4.若A(﹣3,y1),B(﹣1,y2),C(2,y3)都在函数的图象上,则( )
A.y2<y1<y3 B.y3<y2<y1 C.y1<y2<y3 D.y3<y1<y2
5.如图,菱形ABCD的对角线AC,BD交于点P,且AC过原点O,AB∥x轴,点C的坐标为(12,6),反比例函数的图象经过A,P两点,则k的值是( )
A.12 B.9 C.8 D.2
6.如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数0)的图象经过顶点D,分别与对角线AC、边BC交于点E,F,连接AF.若点E为AC的中点,则△ACF的面积为( )
A. B.1 C. D.3
7.如图,在平面直角坐标系中,Rt△OAB的一条边OA在y轴上,OA=4,AB=3,将△OAB向右平移,某一时刻,反比例函数的图象恰好经过点A和OB的中点C,则k的值为( )
A.4 B.5 C.6 D.7
8.如图,在平面直角坐标系中,点A,B分别在反比例函数,的图象上,连结AB交y轴于点C,作点B关于x轴的对称点D,连结AD恰好经过坐标原点O,若,则的值为( )
A. B. C. D.
9.函数y=kx﹣3与y=在同一坐标系内的图象可能是( )
A. B.
C. D.
10.已知直线y=kx+b(k≠0)与双曲线交于A(x1,y1),B(x2,y2) 两点,其中x1≠x2,交x轴于点C(x0,0),若x1+x2=0,则x0的值是( )
A.0 B.正数
C.负数 D.随k的变化而变化
11.如图,点A是反比例函数的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
A.3 B.﹣6 C.6 D.﹣3
12.如图,已知点A(1,6)在双曲线y=(k>0)上,动点P在y轴正半轴上,将点A绕点P顺时针旋转90°,点A的对应点为B,若点B恰好落在双曲线上,则点P的坐标为( )
A.(0,3) B.(3,0)或(2.5,0)
C.(0,4)或(0,2.5) D.(0,3)或(0,4)
13.如图,在平面直角坐标系中,直线y=﹣3x+3交x轴于A点,交y轴于B点,以AB为边在第一象限作正方形ABCD,其中顶点D恰好落在双曲线上,现将正方形ABCD沿y轴向下平移a个单位,可以使得顶点C落在双曲线上,则a的值为( )
A. B. C.2 D.
14.如图,分别过反比例函数图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn),作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An﹣1Pn,再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3……,以此类推,则点B20的坐标是( )
A. B. C. D.
15.如图,在平面直角坐标系中,四边形OABC是矩形,且A(﹣6,0),S矩形OABC=24.反比例函数的图象与边AB,BC交于点D,E,连接DE,DC,则当△DCE的面积最大时,k的值为( )
A.﹣24 B.﹣12 C.﹣6 D.﹣4
二.填空题(共25小题)
16.函数的图象上有两点P1(﹣1,y1),P2(﹣2,y2),若y1<y2,写出一个符合题意的k的值: .
17.若反比例函数y=(m+2)x|m|﹣5的图象在第一、三象限,则m的值为 .
18.某商场销售一批散装坚果,进价为30元每斤,在销售时售货员发现坚果的日销量和每斤的利润正好成反比例关系,且价格调整为每斤50元时,当日销量为80斤,那么每日该坚果的销量y(单位:斤)与每斤价格x(单位:元)之间的函数表达式为 .
19.如图,反比例函数的图象与Rt△BOC的斜边OB交于点A,与边BC交于点D,若,且S△BOD=21,则k= .
20.如图,直线y=kx(k<0)与双曲线交于 A(x1,y1)、B(x2,y2)两点,则2x1y2﹣5y2x1的值为 .
21.如图,在△AOB中,AO=AB,点B在x轴上,C、D分别为OA、OB的中点,连接CD,E为CD上任意一点,连接AE、BE,反比例函数的图象经过点A.若△ABE的面积为8,则k的值为 .
22.如图,在平面直角坐标系xOy中,直线y=x与反比例函数的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交x轴于点C,交反比例函数图象于点B,若,则b的值为 .
23.如图, ABCD的顶点B,D在x轴上,AB⊥BD,反比例函数y=的图象经过点A,连接CA并延长交y轴于点E,连接DE,若△ADE的面积为2,则k的值为 .
24.近视眼镜的镜片是凹透镜,研究发现,近视眼镜的度数y(度)与镜片焦距x(米)的关系近似满足,小宇原来佩戴400度近视眼镜,经过一段时间的矫正治疗,复查验光时,所配镜片焦距调整为0.4米,则小宇的眼镜度数 (填“上涨”或“下降”)了 度.
25.某校科技小组进行野外考察,利用铺垫木板的方式通过了一片烂泥湿地,这是因为人和木板对湿地的压力F一定时,人和木板对地面的压强p(Pa)与木板面积S(m2)存在函数关系:(如图所示)若木板面积为0.2m2,则压强为 Pa.
26.如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,4),顶点C的坐标为(3,1),若反比例函数的图象与矩形ABCD有公共点,则k的值可以是 .(写出一个即可)
27.已知反比例函数的表达式为,A(x1,y1)和B(x2,y2)是反比例函数图象上两点,若x1<0<x2时,y1<y2,则m的取值范围是 .
28.小海利用杠杆平衡原理称药品质量(杠杆平衡时,动力×动力臂=阻力×阻力臂):如图1,小海发现天平平衡时左盘药品为m克,右盘砝码重20克;如图2,仍旧利用此杠杆,小海将砝码放在左盘,药品放在右盘,此时天平仍旧平衡,测得砝码重5克,右盘药品为n克.则m与n满足的关系式为 .
29.如图,一次函数y=ax+8与反比例函数的图象交于M(m,6)和N(n,2)两点,已知S△MON=8,则k= .
30.如图,已知第一象限的双曲线与正方形OCAE的两边相交于D、B两点,直线过B点.则DE:AD的值是 .
31.如图,已知点M(1,2),N(4,n)(n>0),点P为线段MN上的一个动点,反比例函数(k为常数,x>0)的图象经过点P.
(1)当点P与点M重合时,k= ;
(2)若点P与点N重合时,k=8,此时点Q(0,﹣9)到直线MN的距离为 .
32.如图,点A、D分别在函数图象上,点B、C在x轴上,若四边形ABCD为正方形,且点A在第二象限,则点A的坐标为 .
33.已知反比例函数y=,当2≤x<5时,y的取值范围是 .
34. 如图,△ABC的顶点A在反比例函数 的图象上,顶点C在y轴上,AB∥y轴,若点B的坐标为(﹣2,2),S△ABC=4,则k的值为 .
35.如图,在平面直角坐标系中,反比例函数(k为常数,k≠0)的图象经过 ABCD的顶点B,AB交y轴于点E,AB∥x轴,F为CD边上一点,AE:CF:DF=1:2:3,连结FA并延长交x轴于点G,连结DG.
(1)设△ADF的面积S1,四边形ABCF的面积为S2,则S1:S2的值为 ;
(2)当△ADG的面积为3时,k的值为 .
36.如图,A,B为反比例函数第一象限图象上任意两点,连结BO并延长交反比例函数图象另一支于点C,连结AC交x轴于点F,交y轴于点G,连结BG,连结AB并向两侧延长分别交x轴于点E,交y轴于点D.已知,S△OBG=3,则= ,k的值为 .
37.如图,在平面直角坐标系中,放置一个等腰Rt△ABC纸片,∠A=90°,BC边与x轴重合,点A坐标为(3,2),若反比例函数与AB边交于点D,与AC边交于点E.
(1)当点D为AB中点时,反比例函数的表达式为 ;
(2)将如图放置的△ABC纸片的∠B沿过点D的直线翻折,当点B落到AC中点时,k= ;
(3)若双曲线与折线AD、AE所围成的区域内(含边界)有2个横纵坐标都是整数的点,则k的取值范围是 .
38.如图,点A,B分别在第一,二象限的反比例函数图象y=(k1>0),y=(k2<0)上,点C在y轴负半轴上,连结AB,OA,AC,且AC交x轴于点E.已知AB=2AC,CE=2AE,且∠AOC=135°.若AC⊥AB,且k1+k2=﹣,则k2的值为 .
39.已知过原点的一条直线l与反比例函数的图象交于A,B两点(A在B的右侧).C是反比例函数图象上位于A点上方的一动点,连接AC并延长交y轴于点D,连接CB交y轴于点E.若AC=mCD,BC=nCE,则m﹣n= .
40.如图,在平面直角坐标系中,菱形OABC的边OC在x轴负半轴上,函数y=(x<0)的图象经过顶点A和对角线OB的中点M,作AN∥OB交y轴于点N,若△CMN的面积为6,则k的值为 .
三.解答题(共20小题)
41.已知反比例函数的图象经过点A(﹣4,﹣2).
(1)求反比例函数表达式;
(2)若点在该函数图象上,求m的值.
42.为了预防H1N1甲型流感,某校对教室采取喷洒药物消毒,在对某教室进行消毒的过程中,先经过5分钟的集中药物喷洒,再封闭教室10分钟,然后打开门窗进行通风,室内每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(分钟)之间的函数关系,在药物喷洒和封闭教室期间,y与x均满足一次函数的关系,在打开门窗通风后y与x满足反比例函数的关系,如图所示.
(1)研究表明,室内空气中的含药量低于3mg/m3时方可进入教室,从封闭教室开始,至少经过多少分钟后学生方可返回教室?
(2)当室内空气中的含药量不低于6mg/m3且特续时间不低于15分钟时,才能完全有效杀灭流感病毒.试通过分析判断此次消毒是否完全有效?
43.如图是某型号冷柜循环制冷过程中温度变化的部分示意图.该冷柜的工作过程是:当冷柜温度达到﹣4℃时制冷开始,温度开始逐渐下降,当温度下降到﹣20℃时制冷停止,温度开始逐渐上升,当温度上升到﹣4℃时,制冷再次开始,…,按照以上方式循环工作.通过分析发现,当0≤x<4时,温度y是时间x的一次函数;当4≤x<t时,温度y是时间的反比例函数.
(1)求t的值;
(2)当前冷柜的温度﹣10℃,经过多长时间温度下降到﹣20℃?
44.如图在平面直角坐标系中,一次函数y=kx+b的图象经过点A(0,﹣4)、B(2,0)交反比例函数的图象于点C(3,a),点P在反比例函数的图象上,横坐标为n(0<n<3),PQ∥y轴交直线AB于点Q,连接OP、OQ.
(1)求一次函数和反比例函数的表达式;
(2)求△OPQ面积的最大值.
45.在平面直角坐标系xOy中,直线y1=﹣2x+1与反比例函数图象的一个交点为点M.
(1)当点M的坐标为(2,m)时,求k的值;
(2)当x<﹣1时,对于x的每一个值,都有y1>y2,求k的取值范围.
46.如图,已知正比例函数y1=x的图象与反比例函数y2=的图象相交于点A(3,n)和点 B.
(1)求n和k的值;
(2)请结合函数图象,直接写出不等式x﹣<0的解集;
(3)如图,以AO为边作菱形AOCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE、OE,求△AOE的面积.
47.已知直线y1=k1x+b与双曲线相交于点P(﹣2,1)、Q(1,m).
(1)求k1,b,k2的值;
(2)在同一坐标系中画出直线y1=k1x+b与双曲线,根据图写出不等式k1x+b的解集.
48.已知反比例函数(k为常数,k≠0)与正比例函数y2=x的图象有一个交点为P(3,m).
(1)求k的值;
(2)将点P向下平移6个单位,再向左平移5个单位后,得点P′,试判断点P′是否在函数y1的图象上,并说明理由;
(3)当y1>y2时,利用函数图象直接写出自变量x的取值范围.
49.如图,已知点A(1,4),B(7,1),点P作线段AB上,并且点P的横、纵坐标均为整数.经过点P的双曲线为.
(1)当点P与点B重合时,求L的表达式;
(2)求线段AB所在直线的函数表达式;
(8)直接写出k的最小值和最大值.
50.如图,一次函数y=kx+b(k≠0)与反比例函数的图象交于点A(3,4),B(a,﹣2).
(1)求一次函数和反比例函数的解析式;
(2)求不等式的解集;
(3)连接BO并延长,交反比例函数图象于点C,连接AC,求△ABC的面积.
51.如图,在平面直角坐标系中,反比例函数y=(x>0)与一次函数y=ax+b(a≠0)的图象相交于点A(2,m)与点B(4,2).
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上是否存在一点P,使得AP+BP最小,若存在,求出点P坐标;若不存在,请说明理由.
52.在平面直角坐标系中,已知一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,且与反比例函数的图象在第一象限内交于P,K两点,连接OP,△OAP的面积为.
(1)求一次函数与反比例函数的解析式;
(2)若C为线段OA上的一个动点,当PC+KC最小时,求△PKC的面积.
53.如图,在Rt△ABC中,AC=8,BC=4,AC⊥x轴,垂足为C,AB边与y轴交于点D,反比例函数的图象经过点A.
(1)若点D是AB边的中点,求直线AB和反比例函数的表达式.
(2)将AB边沿AC边所在直线翻折,交反比例函数的图象于点E,交x轴于点F,若点E的纵坐标为2,求k的值.
54.如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=的图象交于A、B两点,已知点A的坐标是(﹣2,m+3),点B的坐标是(4,m).
(1)求反比例函数与一次函数的表达式;
(2)求△AOB的面积;
(3)当kx+b>时,x的取值范围是 .
55.如图,一次函数y=﹣2x+1与反比例函数的图象在第二象限交于点A,且点A的横坐标为﹣1.
(1)求反比例函数的解析式;
(2)点B的坐标是(﹣2,0),若点P在y轴上,且△AOP的面积与△AOB的面积相等,求点P的坐标.
56.如图1,有一块边角料ABCDE,其中AB,BC,DE,EA是线段,曲线CD可以看成反比例函数图象的一部分.小宁想利用这块边角料截取一个面积最大的矩形MNQP,其中M,N在AE上(点M在点N左侧),点P在线段BC上,点Q在曲线CD上.测量发现:∠A=∠E=90°,AE=5,AB=DE=1,点C到AB,AE所在直线的距离分别为2,4.
(1)小宁尝试建立坐标系来解决该问题,通过思考,他把A,B,C,D,E这5个点先描到平面直角坐标系上,记点A的坐标为(﹣1,0);点B的坐标为(﹣1,1).
请你在图2中补全平面直角坐标系并画出图形ABCDE;
(2)求直线BC,曲线CD的解析式;
(3)求矩形MNQP的最大面积.
57.如图,在平面直角坐标系xOy中,直线l:y=x+b与x轴、y轴分别交于点A、B,与双曲线H:y=交于点P(2,),直线x=m分别与直线l和双曲线H交于点E、D.
(1)求k和b的值;
(2)当点E在线段AB上时,如果ED=BO,求m的值;
(3)如果△BDE是以BE为腰的等腰三角形,求点E的坐标.
58.如图,已知直线y=x﹣2与x轴交于A点,与y轴交于B点,P(m,n)为双曲线上一动点,过P点分别作x轴,y轴的垂线,垂足分别为C,D,射线PC交直线AB于点E,射线PD交直线AB于点F.
(1)当DF=PC时,求m的值;
(2)连接OE,OF,求证:∠EOF的度数为45°;
(3)在双曲线上有一点Q(不与点P重合),连接PQ,有PQ∥AB,将线段PQ沿直线AB翻折得到线段P′Q′.若线段P′Q′与坐标轴没有交点,求此时n的取值范围.
59.一次函数y=﹣2x+6与反比例函数(k>0,k为常数)的图象交点为A(a,4)和点B,点C是反比例函数(k>0,k为常数)在第三象限内的图象上一点.
(1)求反比例函数的解析式和点B的坐标;
(2)若点C为直线OB与反比例函数的另一个交点,求△ACB的面积;
(3)我们将对角线相等且互相垂直的四边形称为“等直四边形”.如图2,在平面内一点D,AB∥CD,且四边形ABCD为“等直四边形”,求点C的坐标.
60.一、问题背景:
数学活动课上,老师拿出一个由五连格边长为1的正方形连成的L形教具,将它放入一个的直角三角形中,
∠BCA=90°,∠B=30°,如图1顶点D,E,F,G刚好落在三边上,请求出此直角三角形的面积.
二、问题提出与解决:(以下问题二选一解答)
(1)小颖同学受到启发,将此教具放入如图的直角坐标系中,顶点A,B,C分别落在坐标轴上,提出问题:如图2,如果反比例函数图象经过顶点D,试求出反比例解析式.
(2)小明同学也受到启发,画了一个圆,如图3,将此教具放入圆内,使圆经过其顶点A,B,C,提出问题:怎么算出圆的面积?
参考答案与试题解析
一.选择题(共15小题)
1.已知反比例函数的图象经过点(2,3),则下列描述正确的是( )
A.y的值随x值的增大而减小
B.图象位于第二、四象限
C.当x>0时,y<0
D.点(3,2)在图象上
【分析】根据已知求出k,再根据反比例函数的性质逐一判断即可.
【解答】解:∵反比例函数的图象经过点(2,3),
∴k=2×3=6,
∴在每个象限内,y的值随x值的增大而减小,
而A缺少在每个象限这个条件,故A错误;
∵k>0,
∴图象位于一、三象限,故B错误;
当x>0时,y<0,满足第四项象限特征,故C错误;
点(3,2)满足3×2=6=k,故D正确.
故选:D.
【点评】本题考查了反比例函数的图象及性质,求出k值是解题关键.
2.若点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数的图象上,若x1<x2<0<x3则y1,y2,y3的大小关系是( )
A.y2<y1<y3 B.y3<y2<y1 C.y1<y2<y3 D.y3<y1<y2
【分析】先根据反比例函数y=﹣的中k的符号判断出此函数图象所在象限,再根据x1<x2<0<x3判断出y1,y2,y3的大小关系即可.
【解答】解:∵反比例函数y=﹣中,k=﹣1<0,
∴此函数图象在二四象限,且在每一象限内y随x的增大而增大,
∵x1<x2<0<x3,
∴y3<0,y3<0<y1<y2,
∴y3<y1<y2.
故选:D.
【点评】本题考查的是反比例函数图象上点的坐标特点,根据函数解析式判断出函数图象所在的象限是解答此题的关键.
3.如图,点A(m,m+1),B(m+3,m﹣1)都在反比例函数的图象上,则k的值为( )
A.3 B.6 C.14 D.12
【分析】根据同一反比例函数图象上横纵坐标的积为定值解答即可.
【解答】解:∵点A(m,m+1),B(m+3,m﹣1)都在反比例函数的图象上,
∴m(m+1)=(m+3)(m﹣1),
解得m=3,
∴点A(3,4),B(6,2),
∴k=3×4=12,
故选:D.
【点评】本题考查反比例函数图象和性质,熟练掌握同一反比例函数图象上点的横纵坐标的积都相等,都等于反比例函数的比例系数.
4.若A(﹣3,y1),B(﹣1,y2),C(2,y3)都在函数的图象上,则( )
A.y2<y1<y3 B.y3<y2<y1 C.y1<y2<y3 D.y3<y1<y2
【分析】根据反比例函数图象的性质判断出点的位置,再利用函数特点具体判断即可.
【解答】解:∵k=2023>0,
∴函数图象位于一、三象限,
∵﹣3<0,﹣1<0,2>0,
∴点A、B在第三象限,点C在第一象限,
∴y3为正,y1、y2为负,
∵每个象限内,y随x的增大而减小,且﹣3<﹣1,
∴y1>y2,
∴y2<y1<y3,
故选:A.
【点评】本题考查了反比例函数图象的性质,灵活的运用函数图象的性质是解题的关键.
5.如图,菱形ABCD的对角线AC,BD交于点P,且AC过原点O,AB∥x轴,点C的坐标为(12,6),反比例函数的图象经过A,P两点,则k的值是( )
A.12 B.9 C.8 D.2
【分析】先根据反比例函数的对称性和菱形的性质得到,,进而求得点P坐标即可求解.
【解答】解:∵菱形ABCD的对角线AC,BD交于点P,
∴AP=PC,
∵反比例函数的图象经过A,P两点,
∴,则,
过点P、C分别作CE⊥x轴,PF⊥x轴,垂足为E,F,则PF∥CE,
∴△OPF∽△OCE,
∴,
∵点C的坐标为(12,6),
∴OE=12,CE=6,
∴OF=4,PF=2
∴点P坐标为(4,2),
∴k=4×2=8,
故选:C.
【点评】本题考查了反比例函数与几何综合,解决本题的关键是综合利用相似三角形的判定和性质、反比例函数的图象和性质、菱形的性质等,属于基础综合题型,难度适中.
6.如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数0)的图象经过顶点D,分别与对角线AC、边BC交于点E,F,连接AF.若点E为AC的中点,则△ACF的面积为( )
A. B.1 C. D.3
【分析】设D(m,),根据已知条件表示出点E(2m,),点F(3m,),易得CF=,AB=2m,根据三角形面积公式即可得到S△ACF===.
【解答】解:设D(m,),
∵ABCD是矩形,且点E为AC的中点,
∴E点纵坐标为,
代入反比例函数解析式得x=2m,
∴E(2m,),
∴B点横坐标为3m,
∴F点横坐标为3m,代入反比例函数解析式,
得y=,
∴F(3m,),
∴CF=﹣=,
∵AB=3m﹣m=2m,
∴S△ACF===,
故选:A.
【点评】本题主要考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,矩形的性质,设D点坐标根据中点坐标公式表示线段CF和AB的长是解决本题的关键.
7.如图,在平面直角坐标系中,Rt△OAB的一条边OA在y轴上,OA=4,AB=3,将△OAB向右平移,某一时刻,反比例函数的图象恰好经过点A和OB的中点C,则k的值为( )
A.4 B.5 C.6 D.7
【分析】根据题意表示出平移后的点A(a,4),C(+a,2),代入即可求得k的值.
【解答】解:∵Rt△OAB的一条边OA在y轴上,OA=4,AB=3,
∴A(0,4),B(3,4),
∴OB的中点C(,2),
设△OAB向右平移a个单位,则平移后的点A(a,4),C(+a,2),
∵反比例函数的图象恰好经过点A(a,4),C(+a,2),
∴k=4a=2(+a),
解得a=,
∴k=4a=6,
故选:C.
【点评】本题考查了反比例函数图象上点的坐标特征,坐标于图形的变化﹣平移,正确表示出点的坐标是解题的关键.
8.如图,在平面直角坐标系中,点A,B分别在反比例函数,的图象上,连结AB交y轴于点C,作点B关于x轴的对称点D,连结AD恰好经过坐标原点O,若,则的值为( )
A. B. C. D.
【分析】作AE⊥x轴于E,设A(m,),B(n,),则OE=m,AE=,OF=﹣n,FD=FB=,由题意可知BD∥OC,根据平行线分线段成比例定理得出,通过证得△ODF∽△OAE,得出,即可得出,解得=﹣.
【解答】解:作AE⊥x轴于E,
∵点B、D关于x轴的对称,
∴BD⊥x轴,
∴BD∥OC,
∴,
∵AE∥BD,
∴△ODF∽△OAE,
∴,
设A(m,),B(n,),则OE=m,AE=,OF=﹣n,FD=FB=,
∴,
∴=﹣.
故选:D.
【点评】本题考查了反比例函数图象上点的坐标特征,反比例函数的性质,关于x轴对称的点的坐标,三角形相似的判定和性质,正确表示出线段的长度是解题的关键.
9.函数y=kx﹣3与y=在同一坐标系内的图象可能是( )
A. B.
C. D.
【分析】根据当k>0、当k<0时,y=kx﹣3和y=(k≠0)经过的象限,二者一致的即为正确答案.
【解答】解:∵当k>0时,y=kx﹣3过一、三、四象限,反比例函数y=过一、三象限,
当k<0时,y=kx﹣3过二、三、四象限,反比例函数y=过二、四象限,
∴B正确;
故选:B.
【点评】本题主要考查了反比例函数的图象性质和一次函数的图象性质,关键是由k的取值确定函数所在的象限.
10.已知直线y=kx+b(k≠0)与双曲线交于A(x1,y1),B(x2,y2) 两点,其中x1≠x2,交x轴于点C(x0,0),若x1+x2=0,则x0的值是( )
A.0 B.正数
C.负数 D.随k的变化而变化
【分析】根据直线l与x轴交于C(x0,0),当得到x0=﹣,解方程组,得到kx2+bx+4=0,于是得到x1+x2=﹣,即可得到x1+x2=x0,由x1+x2=0,即可得到x0=0.
【解答】解:直线l:y=kx+b(k≠0)交x轴于C(x0,0),
∴x0=﹣,
由消去y得到kx+b=﹣,
∴kx2+bx+4=0,
∴x1+x2=﹣,
∴x1+x2=x0,
∵x1+x2=0,
∴x0=0.
故选:A.
【点评】本题考查了反比例函数与一次函数的交点问题,熟知函数与方程的关系是解题的关键.
11.如图,点A是反比例函数的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是( )
A.3 B.﹣6 C.6 D.﹣3
【分析】连接OA,如图,利用三角形面积公式得到S△OAB=S△CAB=3,再根据反比例函数的比例系数k的几何意义得到=3,然后去绝对值即可得到满足条件的k的值.
【解答】解:连接OA,如图,
∵AB⊥x轴,
∴OC∥AB,
∴S△OAB=S△CAB=3,
而S△OAB=|k|,
∴=3,
∵k<0,
∴k=﹣6.
故选:B.
【点评】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
12.如图,已知点A(1,6)在双曲线y=(k>0)上,动点P在y轴正半轴上,将点A绕点P顺时针旋转90°,点A的对应点为B,若点B恰好落在双曲线上,则点P的坐标为( )
A.(0,3) B.(3,0)或(2.5,0)
C.(0,4)或(0,2.5) D.(0,3)或(0,4)
【分析】先把A(1,6)代入反比例函数y=(k>0)求出k的值,分别过A、B两点作x轴的垂线AC,BD,由旋转的性质证明△APC≌△PBD,再设P(0,m),即可得出B的坐标,由双曲线上的点横坐标与纵坐标的积即相等,列方程求m的值,确定P点坐标.
【解答】解:分别过A、B两点作AC⊥y轴,BD⊥y轴,垂足为C、D,
∵点A(1,6)在双曲线y=(k>0)上,
∴k=1×6=6,
∴反比例函数的解析式为y=,
∵∠APB=90°,
∴∠APC+∠BPD=90°,
又∠APC+∠PAC=90°,
∴∠PAC=∠BPD,
在△APC和△PBD中,
,
∴△APC≌△PBD(AAS),
∴CP=BD,AC=PD=1,
设P(0,m),
∴OP=m,
∴PC=6﹣m,
∴B(6﹣m,m﹣1),
∵点B在双曲线上,
∴m﹣1=,
解得m=3或m=4,
∴P(0,3)或(0,4).
故选:D.
【点评】本题考查的是反比例函数图象上点的坐标特点,坐标与图形变化﹣旋转,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
13.如图,在平面直角坐标系中,直线y=﹣3x+3交x轴于A点,交y轴于B点,以AB为边在第一象限作正方形ABCD,其中顶点D恰好落在双曲线上,现将正方形ABCD沿y轴向下平移a个单位,可以使得顶点C落在双曲线上,则a的值为( )
A. B. C.2 D.
【分析】作CE⊥y轴于点E,作DF⊥x轴于点F,作CH⊥x轴于点H,交双曲线于点G,由函数解析式确定B的坐标是(0,3),A的坐标是(1,0),根据全等三角形的判定和性质得出△OAB≌△FDA≌△BEC,AF=OB=EC=3,DF=OA=BE=1,结合图形求解即可.
【解答】解:作CE⊥y轴于点E,作DF⊥x轴于点F,作CH⊥x轴于点H,交双曲线于点G
在y=﹣3x+3中,
令x=0,解得:y=3,
即B的坐标是(0,3),
令y=0,解得:x=1,
即A的坐标是(1,0),
则OB=3,OA=1.
∵∠BAD=90°,
∴∠BAO+∠DAF=90°,
∵直角△ABO中,∠BAO+∠OBA=90°,
∴∠DAF=∠OBA,
在△OAB和△FDA中,
,
∴△OAB≌△FDA(AAS),
同理,△OAB≌△FDA≌△EBC,
∴AF=OB=EC=3,DF=OA=BE=1,
故D的坐标是(4,1),C的坐标是(3,4),
代入y=得:k=4,
则函数的解析式是:y=.
∴OE=4,
则C的纵坐标是4,
把x=3代入y=得:y=.即G的坐标是,
∴CG=4﹣=,
∴a=,
故选:A.
【点评】本题考查反比例函数与一次函数综合问题,全等三角形的判定和性质等,理解题意,综合运用这些知识点是解题关键.
14.如图,分别过反比例函数图象上的点P1(1,y1),P2(2,y2),…Pn(n,yn),作x轴的垂线,垂足分别为A1,A2,…An,连结A1P2,A2P3,…An﹣1Pn,再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3……,以此类推,则点B20的坐标是( )
A. B. C. D.
【分析】根据反比例函数图象上点的坐标特征求得点P1、P2的纵坐标,由平行四边形对边平行且相等的性质求得点B1的横坐标为2,纵坐标是y2+y1、B2的横坐标为3,纵坐标是y3+y2、B3的横坐标为4,纵坐标是y4+y3,据此可以推知点Bn的横坐标为n+1,纵坐标是:yn+1+yn=+=.
【解答】解:∵点P1(1,y1),P2(2,y2)在反比例函数图象上,
∴y1=4,y2=2;
∴P1A1=y1=4;
又∵四边形A1P1B1P2是平行四边形,
∴P1A1=B1P2=4,P1A1∥B1P2,
∴点B1的纵坐标是:y2+y1=+=6,即点B1的坐标是(2,6);
同理求得,点B2的纵坐标是:y3+y2=+=;即点B2的坐标是(3,);
点B3的纵坐标是:y4+y3=+=;
…
点Bn的横坐标为:xn=n+1,纵坐标是:yn+1+yn=+=;
∴点B20的坐标是(21,)
故选:D.
【点评】本题考查反比例函数图象上点的坐标特征、反比例函数的图象.解答此题的关键是根据平行四边形的对边平行且相等的性质求得点Bn的纵坐标yn+1+yn.
15.如图,在平面直角坐标系中,四边形OABC是矩形,且A(﹣6,0),S矩形OABC=24.反比例函数的图象与边AB,BC交于点D,E,连接DE,DC,则当△DCE的面积最大时,k的值为( )
A.﹣24 B.﹣12 C.﹣6 D.﹣4
【分析】根据图中的点的坐标表示出三角形的面积,得到关于k的二次函数,利用二次函数求出最值即可.
【解答】解:∵A(﹣6,0),S矩形OABC=24,
∴OA=6,
∴OC=4,
∴C(0,4),
∴D(﹣6,),E(,4),
∴CE=﹣,BD=4+,
∴S△DCE=CE BD= (﹣)(+4)=﹣k2﹣k=﹣(k+12)2+3,
∴当k=﹣12时,△ADE的面积最大.
故选:B.
【点评】本题考查了反比例函数函数图象上点的坐标特征,矩形的性质,表示出△DCE的面积是解本题的关键.
二.填空题(共25小题)
16.函数的图象上有两点P1(﹣1,y1),P2(﹣2,y2),若y1<y2,写出一个符合题意的k的值: 2(答案不唯一) .
【分析】根据反比例函数的增减性判断即可.
【解答】解:对于函数的图象上有两点P1(﹣1,y1),P2(﹣2,y2),
∵当﹣1>﹣2时,y1<y2,
∴反比例函数在每个象限内,y随x的增大而减小,
∴k>0,
∴符合题意的k值可以为大于0的任意数,
故答案为:2(答案不唯一).
【点评】本题考查反比例函数的图象与性质,熟知反比例函数的增减性是解答的关键.
17.若反比例函数y=(m+2)x|m|﹣5的图象在第一、三象限,则m的值为 2 .
【分析】根据反比例函数的图象与性质可得到关于m的不等式,解不等式即可求得m的取值范围.
【解答】解:∵反比例函数y=(m+2)x|m|﹣5的图象在第一、三象限,
∴|m|﹣5=﹣1,
解得:m=2 或m=﹣2,
∵m+2≠0,
∴m≠﹣2,
∴m=2.
故答案为:2.
【点评】本题考查了反比例函数的图象与性质,正确地求得m的值是解题的关键.
18.某商场销售一批散装坚果,进价为30元每斤,在销售时售货员发现坚果的日销量和每斤的利润正好成反比例关系,且价格调整为每斤50元时,当日销量为80斤,那么每日该坚果的销量y(单位:斤)与每斤价格x(单位:元)之间的函数表达式为 y= .
【分析】由题意知:坚果的日销量和每斤的利润正好成反比例关系,可设y=,把x=50,y=80代入求出k即可得到结果.
【解答】解:∵坚果的日销量和每斤的利润正好成反比例关系,
∴y与(x﹣30)成反比例关系,
设y=(k>0),
∵x=50时,y=80,
∴=80,
解得,k=1600,
∴y与x之间的函数表达式为:y=,
故答案为:y=.
【点评】本题考查了反比例函数的实际应用,根据题意先构造函数模型,利用待定系数法求出函数解析式是常用方法.
19.如图,反比例函数的图象与Rt△BOC的斜边OB交于点A,与边BC交于点D,若,且S△BOD=21,则k= 8 .
【分析】先设A点的坐标,然后利用求出点B的坐标,再求点D的坐标,从而得到CD和BD的长度,进而得到△COD和△BDO的面积比,最后求出△COD的面即,求出k的值.
【解答】解:设A(2a,),
∵=,
∴=,
∴B(5a,),
∵BC⊥x轴,点D在反比例函数的图象上,
∴D(5a,),S△COD=|k|,
∴CD=,BD=﹣=,
∴===,
∵S△BOD=21,
∴S△COD=4,
∴|k|=4,
∴k=8或k=﹣8(舍去),
故答案为:8.
【点评】本题考查了反比例函数的比例系数k的几何意义,反比函数的性质,解题的关键是通过设点A的坐标从而求得点C的坐标.
20.如图,直线y=kx(k<0)与双曲线交于 A(x1,y1)、B(x2,y2)两点,则2x1y2﹣5y2x1的值为 ﹣6 .
【分析】先根据A(x1,y1),B(x2,y2)双曲线y=﹣上的点可知x1y1=﹣2,x2y2=﹣2,再根据反比例函数与正比例函数均关于原点对称可知x1=﹣x2,y1=﹣y2,故可知x1y2=﹣x1y1,x2y1=﹣x2y2,把此关系式代入所求代数式求解即可.
【解答】解:∵A(x1,y1),B(x2,y2)双曲线y=﹣上的点,
∴x1y1=﹣2,x2y2=﹣2,
∵直线y=kx(k<0)与双曲线y=交于A(x1,y1),B(x2,y2)两点,
∴x1=﹣x2,y1=﹣y2,
∴x1y2=﹣x1y1,x2y1=﹣x2y2,
∴2x1y2﹣5x2y1=﹣2x1y1+5x2y2=(﹣2)×(﹣2)+5×(﹣2)=﹣6.
故答案为:﹣6.
【点评】本题考查的是反比例函数与一次函数的交点问题,根据题意得出x1y2=﹣x1y1,x2y1=﹣x2y2是解答此题的关键.
21.如图,在△AOB中,AO=AB,点B在x轴上,C、D分别为OA、OB的中点,连接CD,E为CD上任意一点,连接AE、BE,反比例函数的图象经过点A.若△ABE的面积为8,则k的值为 ﹣16 .
【分析】连接AD,则可得AD⊥OB,再由中位线定理得CD∥AB,从而可得△ABD的面积等于△ADO的面积,由反比例函数比例系数k的几何意义即可求得k的值.
【解答】解:如图,连接AD,
∵AO=AB,D为OB的中点,
∴AD⊥OB,S△ADO=S△ABD,
∵C、D分别为OA、OB的中点,
∴CD∥AB,
∴S△ADO=S△ABD=S△ABE=8,
由反比例函数比例系数k的几何意义得|k|=2S△ADO=16,
∵k>0,
∴k=﹣16.
故答案为:﹣16.
【点评】本题考查了等腰三角形的性质,三角形中位线定理,等底等高的三角形面积相等,反比例函数比例系数的几何意义等知识,连接AD,由中位线定理得到△ABE的面积转化为与之相等的△ADO的面积是解题的关键.
22.如图,在平面直角坐标系xOy中,直线y=x与反比例函数的图象交于点A,将直线y=x沿y轴向上平移b个单位长度,交x轴于点C,交反比例函数图象于点B,若,则b的值为 .
【分析】解析式联立,解方程求得A的横坐标,根据定义求得B的纵坐标,把纵坐标代入反比例函数的解析式求得B的坐标,代入y=x+b即可求得b的值.
【解答】解:∵直线y=x与反比例函数的图象交于点A,
∴联立,解得或,
∴A(1,1),
∴,
∵,
∴,
过B作BM⊥x轴于M,
∵将直线y=x沿y轴向上平移b个单位长度,交x轴于点C,
∴∠BCM=∠CBM=45°,
∴,
∴B的纵坐标为2,
把y=2代入得,,
∴,
∵将直线y=x沿y轴向上平移b个单位长度,得到直线y=x+b,
∴把代入y=x+b得,求得,
故答案为:.
【点评】本题是反比例函数与一次函数的交点问题,考查了反比例函数图象上点的坐标特征,一次函数的图象与几何变换,求得交点B的坐标是解题的关键.
23.如图, ABCD的顶点B,D在x轴上,AB⊥BD,反比例函数y=的图象经过点A,连接CA并延长交y轴于点E,连接DE,若△ADE的面积为2,则k的值为 4 .
【分析】假设AC,BD相交于点F,设点A的坐标为(a,),BF=m,由△ABF∽△EOF表示出OE,利用S△ADE=S△EFD﹣S△AFD=2即可求出结果.
【解答】解:如图,假设AC,BD相交于点F,设点A的坐标为(a,),BF=m,
∵四边形ABCD是平行四边形,AB⊥x轴,
∴DF=BF=m,OB=a,AB=,
∴OF=a+m,
∵AB∥OE,
∴△ABF∽△EOF,
∴,
∴,
∴EO=,
∵S△ADE=S△EFD﹣S△AFD=DF EO﹣DF AB=DF(EO﹣AB),
∴m()=2,
∴k=4,
故答案为:4.
【点评】本题考查了反比例函数中系数k的几何意义,点的坐标特征,平行四边形的性质,适当设出点的坐标,合理表示出三角形的面积是解题关键.
24.近视眼镜的镜片是凹透镜,研究发现,近视眼镜的度数y(度)与镜片焦距x(米)的关系近似满足,小宇原来佩戴400度近视眼镜,经过一段时间的矫正治疗,复查验光时,所配镜片焦距调整为0.4米,则小宇的眼镜度数 下降 (填“上涨”或“下降”)了 150 度.
【分析】根据眼镜的度数y(度)与镜片焦距x(m)的关系式满足,小宇原来佩戴400度近视眼镜,矫正治疗后所配镜片焦距调整为0.4m,可求出现在小宇佩戴的眼镜度数,两次比较,即可求解.
【解答】解:根据题意得,矫正治疗后所配镜片焦距调整为0.4m,
∴y=
∴y=250.
即矫正治疗后小宇佩戴的眼镜度数是250,小宇原来佩戴400度,
∴400﹣250=150,即下降了150度;
故答案为:下降;150.
【点评】本题主要考查反比例函数的实际运用,将矫正治疗后所配镜片焦距调整为0.4m代入反比例函数求出矫正后的度数,再与原来的度数比较是解题的关键.
25.某校科技小组进行野外考察,利用铺垫木板的方式通过了一片烂泥湿地,这是因为人和木板对湿地的压力F一定时,人和木板对地面的压强p(Pa)与木板面积S(m2)存在函数关系:(如图所示)若木板面积为0.2m2,则压强为 3000 Pa.
【分析】先利用待定系数法求出P关于S的函数解析式,再将S=0.2m2代入计算即可.
【解答】解:由已知反比例函数解析式为P=,
将(0.5,1200)代入,得:1200=,
解得:F=600,
∴P=,
当S=0.2m2时,P=,
解得P=3000,
∴当木板面积为0.2m2时,压强为3000Pa,
故答案为:3000.
【点评】本题主要考查反比例函数的应用,解题的关键是掌握待定系数法求反比例函数解析式.
26.如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,4),顶点C的坐标为(3,1),若反比例函数的图象与矩形ABCD有公共点,则k的值可以是 2(答案不唯一) .(写出一个即可)
【分析】根据矩形写出B,D两点坐标,然后利用双曲线经过点B,D时对应的k值,从而得到k的取值范围.
【解答】解:∵矩形ABCD的顶点A(1,4),C(3,1),
∴B(1,1),D(3,4),
当双曲线经过点B时,k的值最小,此时k=1×1=1,
当双曲线经过点D时,k的值最大,此时k=3×4=12,
∴k的取值范围为1≤k≤12.
∴k可以取2,
故答案为:2(答案不唯一).
【点评】本题考查反比例函数图象上点的坐标特征,熟记点的横纵坐标的积是定值k是解题的关键.
27.已知反比例函数的表达式为,A(x1,y1)和B(x2,y2)是反比例函数图象上两点,若x1<0<x2时,y1<y2,则m的取值范围是 m>﹣1 .
【分析】根据反比例函数的性质,可以得到关于m的不等式,从而可以求得m的取值范围.
【解答】解:∵反比例函数的图象上两点A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2,
∴1+m>0,
解得m>﹣1,
故答案为:m>﹣1.
【点评】本题考查反比例函数图象上点的坐标特征,解答本题的关键是明确题意,利用反比例函数的性质解答.
28.小海利用杠杆平衡原理称药品质量(杠杆平衡时,动力×动力臂=阻力×阻力臂):如图1,小海发现天平平衡时左盘药品为m克,右盘砝码重20克;如图2,仍旧利用此杠杆,小海将砝码放在左盘,药品放在右盘,此时天平仍旧平衡,测得砝码重5克,右盘药品为n克.则m与n满足的关系式为 mn=100 .
【分析】根据“杠杆平衡时,动力×动力臂=阻力×阻力臂”,列出反比例函数的解析式即可.
【解答】解:根据“杠杆平衡时,动力×动力臂=阻力×阻力臂”,
由图1得m OA=20 OB,
∴m=,
由图2得5 OA=n OB,
∴n=,
∴mn=100,
故答案为:mn=100.
【点评】本题考查了反比例函数的应用,正确地求出反比例函数的解析式是解题的关键.
29.如图,一次函数y=ax+8与反比例函数的图象交于M(m,6)和N(n,2)两点,已知S△MON=8,则k= 6 .
【分析】过点M,N分别作x轴的垂线,垂足分别为Q,P,根据题意得出S△OMN=S梯形MNPQ=8,代入M,N的坐标得出n﹣m=2,将M,N代入一次函数,得出a=﹣2,进而求得点M(1,6),根据反比例函数的k的几何意义,即可求解.
【解答】解:如图所示,过点M,N分别作x轴的垂线,垂足分别为Q,P,
依题意,S△OMN+S△ONP=S△OMQ+S梯形MNPQ,
又∵S△ONP=S△OMQ,
∴S△OMN=S梯形MNPQ=8,
∵M(m,6)和N(n,2),
∴,
解得:n﹣m=2,
∵M(m,6)和N(n,2)在y=ax+8上,
∴6=am+8,2=an+8,
∴a(n﹣m)=﹣4,
∴a=﹣2,
∴m=1,
∴M(1,6),
∴k=6,
故答案为:6.
【点评】本题考查了反比例函数的k的几何意义,一次函数与反比例函数交点问题,熟练掌握反比例函数的k的几何意义是解题的关键.
30.如图,已知第一象限的双曲线与正方形OCAE的两边相交于D、B两点,直线过B点.则DE:AD的值是 .
【分析】设,则由正方形的性质得到OC=AC=AE=OE=a,设反比例函数的解析式是,利用待定系数法求出,再由点D的纵坐标是a,进而求出,则,由此即可得到答案.
【解答】解:∵直线经过B点,
∴设,
∵四边形OCAE是正方形,
∴OC=AC=AE=OE=a,
设反比例函数的解析式是,把代入,得,即.
∵在正方形OCAE中,点D在AE上,
∴点D的纵坐标是a,把y=a代入反比例函数的解析式,得,
解得,即,
∵,
∴.
故答案为:.
【点评】本题主要考查了反比例函数与一次函数综合,正方形的性质,正确求出是解题的关键.
31.如图,已知点M(1,2),N(4,n)(n>0),点P为线段MN上的一个动点,反比例函数(k为常数,x>0)的图象经过点P.
(1)当点P与点M重合时,k= 2 ;
(2)若点P与点N重合时,k=8,此时点Q(0,﹣9)到直线MN的距离为 11 .
【分析】(1)把M(1,2)代入计算即可;
(2)求出N点坐标,可得MN∥x轴,即可求出点Q到直线MN的距离.
【解答】解:(1)当点P与点M重合时,P点坐标为(1,2),代入,
得:
解得k=2;
(2)当点P与点N重合时,k=8,,
∴N点坐标为(4,2),
∵M(1,2),
∴MN∥x轴
∴点Q(0,﹣9)到直线MN的距离为:2﹣(﹣9)=11,
故答案为:2,11.
【点评】本题考查反比例函数的性质,将点的坐标代入解析式是解本题的关键.
32.如图,点A、D分别在函数图象上,点B、C在x轴上,若四边形ABCD为正方形,且点A在第二象限,则点A的坐标为 (﹣,3) .
【分析】利用反比例函数图象上点的坐标特征表示AB、BC、CD,再根据正方形的性质求出A坐标即可.
【解答】解:点A、D分别在函数图象上,
∵ABCD是正方形,
∴AB=BC=CD,
∵正方形ABCD的面积为:2+7=9.
∴AB=3,
∴OB=,
∴A的坐标为(﹣,3)
故答案为:(﹣,3).
【点评】本题考查反比例函数图象上点的坐标特征以及正方形的性质,理解反比例函数图象上点的坐标特征以及正方形的性质是正确解答的前提,设出点B,点C坐标,分别表示出正方形的边长是解决问题的关键.
33.已知反比例函数y=,当2≤x<5时,y的取值范围是 2<y≤5 .
【分析】求出x=2和x=5对应的y的值,再根据x的范围求出答案即可.
【解答】解:把x=2代入y=得:y=5,
把x=5代入y=得:y=2,
所以当2≤x<5时,y的取值范围是2<y≤5,
故答案为:2<y≤5.
【点评】本题考查了反比例函数图象上点的坐标特征和反比例函数的性质,能熟记反比例函数的性质是解此题的关键.
34. 如图,△ABC的顶点A在反比例函数 的图象上,顶点C在y轴上,AB∥y轴,若点B的坐标为(﹣2,2),S△ABC=4,则k的值为 ﹣12 .
【分析】利用S△ABC=4,求出AB,再利用点B的坐标求点A的坐标,即可求出k值.
【解答】解:∵B的坐标为(﹣2,2),
∴点B与y轴的距离为2,
∵S△ABC=4,
∴AB=4,
又∵B的坐标为(﹣2,2),
∴点B与x轴的距离为2,
∵AB∥y轴,
∴点A到x轴的距离为6,
∴点A坐标为(﹣2,6),
∴k=﹣2×6=﹣12.
故答案为:﹣12
【点评】本题考查了反比例函数的几何意义,解题的关键是三角形面积的求法.
35.如图,在平面直角坐标系中,反比例函数(k为常数,k≠0)的图象经过 ABCD的顶点B,AB交y轴于点E,AB∥x轴,F为CD边上一点,AE:CF:DF=1:2:3,连结FA并延长交x轴于点G,连结DG.
(1)设△ADF的面积S1,四边形ABCF的面积为S2,则S1:S2的值为 ;
(2)当△ADG的面积为3时,k的值为 8 .
【分析】(1)根据三角形和梯形的面积的同高的关系导出面积之比;
(2)根据同底三角形的面积之比等于高之比,同高三角形的面积之比等于底之比,求出△OBE的面积,再用反比例函数的几何意义求出k.
【解答】解:(1)设:每一份为a,
∵AE:CF:DF=1:2:3,
∴AE=a,CF=2a,DF=3a,
∵四边形ABCD是平行四边形,
∴AB=CD=5a,
设AB和CD之间的距离为h,
∴S1=,S2=(2a+5a) h=,
∴S1:S2==;
故答案为:.
(2)如图,设点D到GF的距离为h1,点B到AF的距离为h2,
连接BF、GE、GB、OB,
∵DF=3a,AB=5a,
∴S△ADF:S△ABF=3:5,即h1:h2=3:5,
∴S△AGD:S△AGB=3:5,
∵S△AGD=3,
∴S△AGB=5,
∵AE:BE=1:4,
∴S△BEG=4,
∴S△BEO=4,
∴=8,
∴k=±8.
∵反比例函数在一、三象限,
∴k=8.
故答案为:8.
【点评】本题考查了图形的面积之比的求法,要求学生有较强的识图能力.
36.如图,A,B为反比例函数第一象限图象上任意两点,连结BO并延长交反比例函数图象另一支于点C,连结AC交x轴于点F,交y轴于点G,连结BG,连结AB并向两侧延长分别交x轴于点E,交y轴于点D.已知,S△OBG=3,则= ,k的值为 .
【分析】如图,设A(a,),B(b,),过点A作AL⊥x轴于点L,AH⊥y轴于点H,过点B作BK⊥x轴于点K,BM⊥y轴于点M,过点C作CN⊥y轴于点N,连接OA,由BK∥AL,可得△EBK∽△EAL,推出:=,即=,再由AH∥BM,可得△DAH∽△DBM,推出=;再证得△BOM≌△CON(AAS),得出BM=CN,即可得==,由AH∥CN,可得△AGH∽△CGN,推出==,进而可得S梯形ABKO=S△AOB=,即k(﹣)=,再结合=,即可求得答案.
【解答】解:如图,设A(a,),B(b,),过点A作AL⊥x轴于点L,AH⊥y轴于点H,过点B作BK⊥x轴于点K,BM⊥y轴于点M,过点C作CN⊥y轴于点N,连接OA,
则AH=a,AL=,BM=b,BK=,
∵BK∥AL,
∴△EBK∽△EAL,
∴=,
∵=,
∴=,
∴=,
∴7BK=2AL,即7×=2×,
∴=,即=,
∵AH∥BM,
∴△DAH∽△DBM,
∴==,
∴=,
∴==,
∴DA=BE=AB,
∴DE=DA+AB+BE=AB,
∴=;
∵B、C关于原点O对称,
∴OB=OC,
∵S△OBG=3,
∴S△BCG=2S△OBG=6,
∵BM∥CN,
∴∠OBM=∠OCN,∠OMB=∠ONC,
∴△BOM≌△CON(AAS),
∴BM=CN,
∴==,
∵AH∥CN,
∴△AGH∽△CGN,
∴==,
∴==,
∴S△ABG=S△BCG=×6=,
∴S△ABC=S△ABG+S△BCG=+6=,
∴S△AOB=S△ABC=×=,
∵S△AOB+S△OBK=S△AOL+S梯形ABKO,S△OBK=S△AOL=k,
∴S梯形ABKO=S△AOB=,
∴(+)(b﹣a)=,
即k =,
∴k(﹣)=,
又∵=,
∴=,
∴k(﹣)=,
∴k=.
故答案为:,.
【点评】本题考查反比例函数的综合应用,反比例函数系数k的几何意义,中心对称性质,三角形面积,全等三角形的判定和性质,相似三角形的判定和性质等知识,本题综合性较强,难度较大,解题的关键是数形结合、方程思想等重要数学思想的应用.
37.如图,在平面直角坐标系中,放置一个等腰Rt△ABC纸片,∠A=90°,BC边与x轴重合,点A坐标为(3,2),若反比例函数与AB边交于点D,与AC边交于点E.
(1)当点D为AB中点时,反比例函数的表达式为 y= ;
(2)将如图放置的△ABC纸片的∠B沿过点D的直线翻折,当点B落到AC中点时,k= ;
(3)若双曲线与折线AD、AE所围成的区域内(含边界)有2个横纵坐标都是整数的点,则k的取值范围是 3<k<4 .
【分析】(1)作AF⊥BC于点F,求出BF=CF=AF=2,得到点B的坐标,利用中点坐标公式求出点D的坐标即可求解;
(2)求出点B′的坐标,求出直线AB的解析式,设D(m,m﹣1),利用勾股定理求出m的值,进而可求出k的值;
(3)数形结合,找出临界点求出k的值即可.
【解答】解:(1)作AF⊥BC于点F,
∵点A坐标为(3,2),OF=3,
∴AF=2,
∵△ABC是等腰直角三角形,AF⊥BC,
∴∠ABF=∠BAF=∠ACF=∠CAF=45°,
∴BF=CF=AF=2,
∴OB=3﹣2=1,OC=3+2=5,
∴B(1,0),
∴xD=,yD==1,
∴D(2,1),
∴k=2×1=2,
∴反比例函数的表达式为y=,
故答案为:y=;
(2)如图,点B落在AC上中点B′处,连接DB′.
由(1)可知,OC=5,
∴C(5,0),
∵点A坐标为(3,2),点B′是AC的中点,
∴B′(4,1),
设直线AB的解析式为y=kx+b,把点A和点B的坐标代入得,
解得,
∴直线AB的解析式为y=x﹣1,
设D(m,m﹣1),
∵BD=B′D,
∴(m﹣1)2+(m﹣1)2=(m﹣4)2+(m﹣1﹣1)2,
解得m=,
∴m﹣1=,
∴D(,),
∴k==.
故答案为:;
(3)∵点A坐标为(3,2),B′(4,1),
∴若双曲线与折线AD、AE所围成的区域内(含边界)有2个横纵坐标都是整数的点,则这两个点一定是点A和点B′,
把(3,1)代入y=得k=3,把(4,1)代入y=得k=4,
∴3<k≤4.
故答案为:3<k≤4.
【点评】本题是反比例函数的综合题,考查了反比例函数和一次函数的交点问题,待定系数法求函数解析式,等腰三角形的性质,以及勾股定理等知识,数形结合是解答本题的关键.
38.如图,点A,B分别在第一,二象限的反比例函数图象y=(k1>0),y=(k2<0)上,点C在y轴负半轴上,连结AB,OA,AC,且AC交x轴于点E.已知AB=2AC,CE=2AE,且∠AOC=135°.若AC⊥AB,且k1+k2=﹣,则k2的值为 ﹣ .
【分析】由∠AOC=135°,则∠AOy=45°,故设点A(m,m),由平行线分线段成比例求出点C(0,﹣2m),利用△BMA∽△ANC得到B的坐标,进而求解.
【解答】解:∵∠AOC=135°,则∠AOy=45°,
故设点A(m,m),
过点A作AT⊥y轴于点T,则OT=m,
∵OE∥AT,CE=2AE,即CE:AE=2,
∴OC:OT=2,故点C(0,﹣2m),
过点A作MN∥y轴交过点B与x轴的平行线于点M,交过点C与x轴的平行线于点N,
∵∠CAN+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠CAN=∠ABM,
∵∠BMA=∠ANC=90°,
∴△BMA∽△ANC,
∵AB=2AC,
则△BMA和△ANC的相似比为2:1,
即BM=2AN,AM=2CN,
设点B(s,t),
则m﹣s=2×(m+2m)且t﹣m=2m,
解得:s=﹣5m且t=3m,
则k2=st=﹣15m2,
而k1=m2,
∵k1+k2=﹣,
即﹣15m2+m2=﹣,
解得:m2=,
则k2=st=﹣15×=﹣,
故答案为:﹣.
【点评】本题考查的是反比例函数综合运用,涉及到一次函数和反比例函数的性质、平行线分线段正比例、三角形相似等,其中,正确设点A的坐标,用三角形相似确定点B坐标得方法,是此类题目解题的一半方法,题目综合性强,难度适中.
39.已知过原点的一条直线l与反比例函数的图象交于A,B两点(A在B的右侧).C是反比例函数图象上位于A点上方的一动点,连接AC并延长交y轴于点D,连接CB交y轴于点E.若AC=mCD,BC=nCE,则m﹣n= ﹣2 .
【分析】过点A作AF⊥y轴于点F,过点C作CM⊥y轴于M,过点B作BN⊥y轴于N,所以CM∥AF∥BN,AC=mCD,所以CM:AF:BN=1:(1+m):(1+m),可得CE:BE=1:(1+m),因为BC=nCE.所以CE:BE=1:(n﹣1),则1+m=n﹣1,整理即可得出结论.
【解答】解:根据题意作出图形,如图所示,
过点A作AF⊥y轴于点F,过点C作CM⊥y轴于M,过点B作BN⊥y轴于N,
∴CM∥AF∥BN,AC=mCD,
∴CM:AF:BN=1:(1+m):(1+m),
∴CE:BE=1:(1+m),
∵BC=nCE.
∴CE:BE=1:(n﹣1),
∴1+m=n﹣1,
∴m﹣n=﹣2.
故答案为:﹣2.
【点评】本题是反比例函数与一次函数的交点问题,考查了反比例函数的性质,反比例函数图象上点的坐标特征,平行线分线段成比例定理,能够正确表示出线段的比是解题的关键.
40.如图,在平面直角坐标系中,菱形OABC的边OC在x轴负半轴上,函数y=(x<0)的图象经过顶点A和对角线OB的中点M,作AN∥OB交y轴于点N,若△CMN的面积为6,则k的值为 16 .
【分析】如图,连接AM,延长BA交y轴于点F,点A,M,C三点共线.BF⊥y轴,设点M(m,n),则B(2m,2n),推出k=mn,推出A(,2n),再证明△AMN的面积=△AON的面积=6.可得 =6.整理得mn=16.
【解答】解:如图,连接AM,延长BA交y轴于点F,
∵点M是菱形对角线OB的中点,AB∥OC,
∴点A,M,C三点共线.BF⊥y轴,
设点M(m,n),则B(2m,2n),
∴k=mn,
∴A(,2n),
∴直线OB:y=x,
∵AN∥OB,
∴直线AN:y=x+.
∴N(0,n).
∴AF=,ON=.
∵点D是AC的中点,
∴△AMN的面积=△CMN的面积=6,
∵AN∥OB,
∴△AMN的面积=△AON的面积=6.
∴ =6.整理得mn=16.
∴k=16.
故答案为:16.
【点评】本题主要考查反比例函数与几何综合问题,涉及待定系数法求函数解析式,三角形的面积,菱形的性质等内容,关键是将△AMN的面积转化为△AON的面积.
三.解答题(共20小题)
41.已知反比例函数的图象经过点A(﹣4,﹣2).
(1)求反比例函数表达式;
(2)若点在该函数图象上,求m的值.
【分析】(1)将点A(﹣4,﹣2)代入求解即可;
(2)将点代入(1)求出的表达式中即可求出m的值.
【解答】解:(1)∵反比例函数的图象经过A(﹣4,﹣2),
∴将A(﹣4,﹣2)代入,得k=﹣4×(﹣2)=8,
∴反比例函数解析式为;
(2)∵点在这个函数图象上,
∴把代入
得,
解得:m=±4,
∴m的值为±4.
【点评】本题主要考查了反比例函数图象上点的性质,解题的关键是熟练掌握反比例函数图象上点的特征.
42.为了预防H1N1甲型流感,某校对教室采取喷洒药物消毒,在对某教室进行消毒的过程中,先经过5分钟的集中药物喷洒,再封闭教室10分钟,然后打开门窗进行通风,室内每立方米空气中含药量y(mg/m3)与药物在空气中的持续时间x(分钟)之间的函数关系,在药物喷洒和封闭教室期间,y与x均满足一次函数的关系,在打开门窗通风后y与x满足反比例函数的关系,如图所示.
(1)研究表明,室内空气中的含药量低于3mg/m3时方可进入教室,从封闭教室开始,至少经过多少分钟后学生方可返回教室?
(2)当室内空气中的含药量不低于6mg/m3且特续时间不低于15分钟时,才能完全有效杀灭流感病毒.试通过分析判断此次消毒是否完全有效?
【分析】(1)当x≥15时,设y与x的函数关系式为:y=(m>o),代入图中点的坐标求出m,令y=3,求出时间x,再减去5分钟即可得结果.
(2)当0≤x≤5时,设y与x的函数关系式为:y=kx(k>0),代入图中点的坐标求出k,令y=6,求出x,对于y=,令y=6,求出时间x,用两时间之差与15作比较,即可得结果.
【解答】解:(1)当x≥15时,设y与x的函数关系式为:y=(m>o),
把(15,8)代入上式得,=8,
∴m=120,
∴y=,
当y=3时,=3,
∴x=40,
40﹣5=35(分钟).
答:至少经过35分钟后学生方可返回教室.
(2)当0≤x≤5时,设y与x的函数关系式为:y=kx(k>0),
把(5,10)代入上式得,5k=10,
∴k=2,
∴y=2x,
当y=6时,2x=6,
∴x=3,
对于y=,当y=6时,=6,
∴x=20,
∵20﹣3=17>15,
∴此次消毒是完全有效,
答:此次消毒完全有效.
【点评】本题考查了反比例函数与一次函数的实际应用,是一个分段函数,涉及待定系数法等知识点.掌握自变量、函数值等知识是解题的关键.
43.如图是某型号冷柜循环制冷过程中温度变化的部分示意图.该冷柜的工作过程是:当冷柜温度达到﹣4℃时制冷开始,温度开始逐渐下降,当温度下降到﹣20℃时制冷停止,温度开始逐渐上升,当温度上升到﹣4℃时,制冷再次开始,…,按照以上方式循环工作.通过分析发现,当0≤x<4时,温度y是时间x的一次函数;当4≤x<t时,温度y是时间的反比例函数.
(1)求t的值;
(2)当前冷柜的温度﹣10℃,经过多长时间温度下降到﹣20℃?
【分析】(1)由函数图象可知当时间为t时,温度与时间之间是反比例函数关系,由图象上(4,﹣20)点求出反比例函数的关系式,再由反比例函数关系式求出当y=﹣4时的t的值即可;
(2)分别求得x=﹣10时的函数值,分类讨论即可求解.
【解答】解:(1)设反比例函数的关系式为.
把(4,﹣20)代入,得:.
∴k=﹣80.
∴.
当y=﹣4时,,
∴t=20.
(2)设一次函数函数的关系式为y=kx﹣4.
把(4,﹣20)代入,得:﹣20=4k﹣4,解得:k=﹣4,
∴y=﹣4x﹣4,
当在温度下降过程中,﹣10=﹣4x﹣4,x=1.5,
∴4﹣1.5=2.5(min)
此时,经过2.5分钟温度可下降到﹣20°C.
当在温度上升过程中时,x=8,
∴20﹣8+4=16(min).
此时,在经过16分钟温度可降至﹣20°C.
【点评】本题考查了一次函数与反比例函数的综合运用,熟练掌握反比例函数的性质是解题的关键.
44.如图在平面直角坐标系中,一次函数y=kx+b的图象经过点A(0,﹣4)、B(2,0)交反比例函数的图象于点C(3,a),点P在反比例函数的图象上,横坐标为n(0<n<3),PQ∥y轴交直线AB于点Q,连接OP、OQ.
(1)求一次函数和反比例函数的表达式;
(2)求△OPQ面积的最大值.
【分析】(1)由A(0,﹣4)、B(2,0)的坐标可求出一次函数的关系式,进而求出点C的坐标,代入,求得反比例函数解析式;
(2)设点,点Q(n,2n﹣4),得出关于PQ与n的关系式,进而根据三角形面积公式求解,根据二次函数的性质即可求得最大值.
【解答】解:(1)把A(0,﹣4)、B(2,0)代入一次函数y=kx+b得:
,
解得:,
∴一次函数的关系式为y=2x﹣4,
将点C(3,a)代入y=2x﹣4,得a=2×3﹣4=2,
∴点C(3,2),
将点C(3,2)代入,
得出m=3×2=6,
∴;
(2)∵点P在反比例函数的图象上,点Q在一次函数的图象上,0<n<3,
设点,点Q(n,2n﹣4),
∴,
∴,
∵﹣1<0,
∴当n=1时,,
所以,△OPQ面积的最大值是4.
【点评】本题考查反比例函数、一次函数的解析式,将面积用函数的数学模型表示出来,利用函数的最值求解是解决问题的基本思路.
45.在平面直角坐标系xOy中,直线y1=﹣2x+1与反比例函数图象的一个交点为点M.
(1)当点M的坐标为(2,m)时,求k的值;
(2)当x<﹣1时,对于x的每一个值,都有y1>y2,求k的取值范围.
【分析】(1)将点M代入y1=﹣2x+1,求出m的值,再将点M坐标代入反比例函数解析式求k的值即可;
(2)根据反比例函数图象上点的坐标特征,分情况讨论:①当k>0时,②当k<0时,分别求解即可.
【解答】解:(1)将点M(2,m)代入y1=﹣2x+1,
得﹣4+1=m,
∴m=﹣3,
∴点M坐标为(2,﹣3),
∴k=2×(﹣3)=﹣6;
(2)如图所示:
①当k>0时,当x<﹣1时,对于x的每一个值,都有y1>y2,
②当k<0时,x=﹣1时,﹣2×(﹣1)+1≥﹣k,
解得﹣3≤k<0,
综上所述,满足条件的k的取值范围是﹣3≤k<0或k>0.
【点评】本题考查了反比例函数与一次函数的交点问题,熟练掌握反比例函数图象上点的坐标特征是解题的关键.
46.如图,已知正比例函数y1=x的图象与反比例函数y2=的图象相交于点A(3,n)和点 B.
(1)求n和k的值;
(2)请结合函数图象,直接写出不等式x﹣<0的解集;
(3)如图,以AO为边作菱形AOCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE、OE,求△AOE的面积.
【分析】(1)先把点A(3,n)代入正比例函数解析式求出n的值,再把求出的点A坐标代入反比例函数解析式即可求出k值;
(2)根据正比例函数和反比例函数都是关于原点成中心对称的,可得出点B的坐标,然后根据图象即可写出解集;
(3)根据题意作出辅助线,然后求出OA的长,根据菱形的性质求出OC的长,可推出,然后求出菱形的面积即可求出△AOE的面积.
【解答】解:(1)把点A(3,n)代入正比例函数可得:n=4,
∴点A(3,4),
把点A(3,4)代入反比例函数,
可得:k=12;
(2)∵点A与点B是关于原点对称的,
∴点B(﹣3,﹣4),
∴根据图象可得,不等式x﹣<0的解集为:x<﹣3或0<x<3;
(3)如图所示,过点A作AG⊥x轴,垂足为G,
∵A(3,4),
∴OG=3,AG=4
在Rt△AOG中,AO==5
∵四边形AOCD是菱形,
∴OC=OA=5,,
∴.
【点评】本题主要考查的是反比例函数的综合题型,解题关键:一是求出反比例函数解析式,二是求出菱形的面积.
47.已知直线y1=k1x+b与双曲线相交于点P(﹣2,1)、Q(1,m).
(1)求k1,b,k2的值;
(2)在同一坐标系中画出直线y1=k1x+b与双曲线,根据图写出不等式k1x+b的解集.
【分析】(1)利用待定系数法即可求得;
(2)作出函数的图象,根据图象即可求得.
【解答】解:(1)∵双曲线经过点P(﹣2,1)、Q(1,m),
∴k2=﹣2×1=1×m,
∴k2=﹣2,m=﹣2,
∴y2=﹣,Q(1,﹣2),
∵直线y1=k1x+b过点P(﹣2,1)、Q(1,﹣2),
∴,
解得
故k1,b,k2的值分别为﹣1,﹣1,﹣2;
(2)如图:
由图象可知,不等式k1x+b的解集为x≤﹣2或0<x≤1.
【点评】本题考查了反比例函数与一次函数的交点、待定系数法求函数的解析式、函数与不等式的关系,熟练掌握待定系数法以及数形结合思想的运用是解题的关键.
48.已知反比例函数(k为常数,k≠0)与正比例函数y2=x的图象有一个交点为P(3,m).
(1)求k的值;
(2)将点P向下平移6个单位,再向左平移5个单位后,得点P′,试判断点P′是否在函数y1的图象上,并说明理由;
(3)当y1>y2时,利用函数图象直接写出自变量x的取值范围.
【分析】(1)由正比例函数的解析式求得点P的坐标,代入数(k为常数,k≠0)即可求得k的值;
(2)求得P′的坐标为(﹣2,﹣3),由﹣2×(﹣3)=6≠k,即可判断点P′不在函数y1的图象上;
(3)利用图象即可求解.
【解答】解:(1)∵正比例函数y2=x的图象过交点为P(3,m),
∴m=3,
∴P(3,3),
∵点P在反比例函数(k为常数,k≠0)的图象上,
∴k=3×3=9;
(2)将点P向下平移6个单位,再向左平移5个单位后,得点P′(﹣2,﹣3),
∵﹣2×(﹣3)=6≠9,
∴点P′不在函数y1的图象上;
(3)由图象可知,当y1>y2时,自变量x的取值范围是x<﹣3或0<x<3.
【点评】本题是反比例函数于一次函数的交点问题,考查了一次函数图象上点的坐标特征,待定系数法求反比例函数的解析式,函数与不等式的关系,数形结合是解题的关键.
49.如图,已知点A(1,4),B(7,1),点P作线段AB上,并且点P的横、纵坐标均为整数.经过点P的双曲线为.
(1)当点P与点B重合时,求L的表达式;
(2)求线段AB所在直线的函数表达式;
(8)直接写出k的最小值和最大值.
【分析】(1)利用待定系数法即可求解;
(2)根据待定系数法求得即可;
(3)根据题意点P的坐标为(1,4)或(3,3)或(5,2)或(7,1),根据图象上点的坐标特征k=xy即可求得k的最小值和最大值.
【解答】解:(1)∵点A(1,4),B(7,1),点P与点B重合,
∴P(7,1),
∵双曲线经过点P,
∴k=7×1=7,
∴L的表达式为y=;
(2)设直线AB的解析式为y=ax+b,
∴,
解得,
∴线段AB所在直线的函数表达式为y=﹣+;
(3)∵点A(1,4),B(7,1),点P在线段AB上,
∴点P坐标为(1,4)或(3,3)或(5,2)或(7,1),
∵经过点P的双曲线为,
∴k的最小值为4,最大值为10.
【点评】本题考查了待定系数法求反比例函数和一次函数的解析式,反比例函数图象上点的坐标特征,熟知反比例函数图象上点的坐标特征是解题的关键.
50.如图,一次函数y=kx+b(k≠0)与反比例函数的图象交于点A(3,4),B(a,﹣2).
(1)求一次函数和反比例函数的解析式;
(2)求不等式的解集;
(3)连接BO并延长,交反比例函数图象于点C,连接AC,求△ABC的面积.
【分析】(1)待定系数法求出一次函数和反比例函数解析式;
(2)通过图象找到所要求的解集区域,再通过交点坐标得出解集;
(3)作水平辅助线把图象分割成两个三角形,再求面积.
【解答】解:(1)反比例函数 (m≠0)的图象双曲线过点A(3,4),
∴m=xy=3×4=12,
∴,
∵双曲线过点B(a,﹣2),
∴﹣2a=12,
∴a=﹣6,
∴点B(﹣6,﹣2),
∵一次函数y=kx+b的图象直线过点A(3,4),B(﹣6,﹣2),
则有
∴,
∴;
(2)由图可知,当﹣6<x<0或x>3时,一次函数的图象在反比例函数的图象上方,
故不等式的解集是:﹣6<x<0或x>3;
(3)如解图,设AB与y轴的交点为D,连接CD.
当x=0时,.
∴D(0,2).
∵反比例函数和正比例函数的图象(直线BC)都关于原点中心对称,
∴这两个函数图象的交点关于原点中心对称,
∵B(﹣6,﹣2).
∴C(6,2),
∴点C和点D的纵坐标相等,
∴CD∥x轴.
∴CD=6.
分别记点A,B,D的纵坐标为yA,yB,yD,
∴ ,
,
∴S△ABC=S△ACD+S△BCD=6+12=18.
【点评】本题考查待定系数法求解析式、一次函数与反比例函数图象的交点、围成的图形面积,掌握反比例函数的图象和性质是本题关键.
51.如图,在平面直角坐标系中,反比例函数y=(x>0)与一次函数y=ax+b(a≠0)的图象相交于点A(2,m)与点B(4,2).
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上是否存在一点P,使得AP+BP最小,若存在,求出点P坐标;若不存在,请说明理由.
【分析】(1)把B点的坐标代入反例函数解析式即可求出反比例函数解析式,进而得出A的坐标,把A、B的坐标代入一次函数解析式即可求出一次函数解析式;
(2)△AOB的面积=△BOD的面积﹣△AOD的面积;
(3)首先求得点B关于x轴的对称点的坐标,然后求得直线AB′的解析式后求得其与x轴的交点即可求得点P的坐标.
【解答】解:(1)∵反比例函数y=(x>0)的图象经过B(4,2),
∴k=4×2=8,
∴反比例函数的表达式为y=,
∵点A(2,m)在y=上,
∴m=4,
∴A点坐标为(2,4);
把A,B两点的坐标代入y=ax+b,得,
解得,
∴一次函数的表达式为:y=﹣x+6;
(2)当x=0时,y=﹣x+6=6,
∴D点坐标为(0,6),
∴S△AOB=S△BOD﹣S△AOD==6,
即△AOB的面积为6;
(3)在x轴上存在点P,使得AP+PB最小.
作点B(4,2)关于x轴的对称点B′(4,﹣2),如图,连接AB′.
设直线AB'的解析式为:y=a′x+b′,
∴,
解得,
∴直线AB'的解析式为:y=﹣3x+10,
令y=0,解得x=,
∴P(,0)可使AP+BP最小.
【点评】本题主要考查了反比例函数和一次函数的交点问题,轴对称﹣最短路线问题.正确运用待定系数法求反比例函数和一次函数的解析式是解题的关键.
52.在平面直角坐标系中,已知一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,且与反比例函数的图象在第一象限内交于P,K两点,连接OP,△OAP的面积为.
(1)求一次函数与反比例函数的解析式;
(2)若C为线段OA上的一个动点,当PC+KC最小时,求△PKC的面积.
【分析】(1)根据待定系数法可求出直线AB的解析式,根据△OAP的面积可得出点P的坐标,代入反比例函数解析式可得出反比例函数的解析式;
(2)作点P关于x轴的对称点P′,连接KP′,线段KP′与x轴的交点即为点C,求出直线KP′的解析式,令y=0,可得出点C的坐标,再根据三角形的面积公式可得出结论.
【解答】解:(1)∵一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,
∴,
解得.
∴一次函数的解析式为:y1=﹣x+,
∵△OAP的面积为.
∴ OA yP=,
∴yP=,
∵点P在一次函数图象上,
∴令﹣x+=,
解得x=4,
∴P(4,).
∵点P在反比例函数的图象上,
∴k2=4×=2.
∴反比例函数的解析式为:y2=;
(2)令﹣x+=,解得x=1或x=4,
∴K(1,2),
作点P关于x轴的对称点P′,连接KP′,线段KP′与x轴的交点即为点C,
∵P(4,).
∴P′(4,﹣).
∴PP′=1,
∴直线KP′的解析式为:y=﹣x+.
令y=0,解得x=.
∴C(,0).
∴S△PKC= (xC﹣xK) PP′
=×(﹣1)×1
=.
∴当PC+KC最小时,△PKC的面积为.
【点评】本题是反比例函数与一次函数的交点问题,主要考查待定系数法求函数解析式,数形结合思想,轴对称最值问题,三角形的面积问题等知识,关键是求出一次函数和反比例函数的解析式.
53.如图,在Rt△ABC中,AC=8,BC=4,AC⊥x轴,垂足为C,AB边与y轴交于点D,反比例函数的图象经过点A.
(1)若点D是AB边的中点,求直线AB和反比例函数的表达式.
(2)将AB边沿AC边所在直线翻折,交反比例函数的图象于点E,交x轴于点F,若点E的纵坐标为2,求k的值.
【分析】(1)根据题意求得A(2,8),B(﹣2,0),然后利用待定系数法即可求得线AB和反比例函数的表达式;
(2)作EH⊥x轴于H,由题意可知CF=BC=4,利用平行线分线段成比例定理得出FH=1,即可求得CH=3,设A(x,8),则E(x+3,2),代入反比例函数解析式得到k=8x=2(x+3),即可求得k=8.
【解答】解:(1)在Rt△ABC中,AC=8,BC=4,AC⊥x轴,垂足为C,
∴AC∥OD,
∵点D是AB边的中点,
∴O为BC的中点,
∴A(2,8),B(﹣2,0),
设直线AB为y=ax+b,
∴,
解得,
∴直线AB为y=2x+4,
∵反比例函数的图象经过点A,
∴k=2×8=16,
∴反比例函数的表达式为y=;
(2)作EH⊥x轴于H,
由题意可知CF=BC=4,
∵点E的纵坐标为2,
∴EH=2,
∵EH∥AC,
∴,即,
∴FH=1,
∴CH=4﹣1=3,
设A(x,8),则E(x+3,2),
∵反比例函数的图象过点A、E,
∴k=8x=2(x+3),
∴x=1,
∴k=8x=8.
【点评】本题是反比例函数与一次函数图象的交点问题,考查了待定系数法求函数的解析式,平行线分线段成比例定理,求得交点坐标是解决问题的关键.
54.如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=的图象交于A、B两点,已知点A的坐标是(﹣2,m+3),点B的坐标是(4,m).
(1)求反比例函数与一次函数的表达式;
(2)求△AOB的面积;
(3)当kx+b>时,x的取值范围是 x<﹣2或0<x<4 .
【分析】(1)根据反比例函数y=的图象经过点A(﹣2,m+3),B(4,m),求出m,n的值,得出反比例函数的解析式,从而求出点A、B的坐标,再根据一次函数y=kx+b的图象经过点A和点B,求出k和b的值,得出一次函数的解析式;
(2)根据三角形的面积公式可得答案;
(3)根据函数的图象和交点坐标即可求得.
【解答】解:(1)∵反比例函数y=的图象经过点A(﹣2,m+3),B(4,m),
∴n=﹣2(m+3)=4m,
∴m=﹣1,
∴A(﹣2,2),B(4,﹣1),n=4m=﹣4,
∴反比例函数的解析式为y=﹣,
∵一次函数y=kx+b的图象经过点A,B,
∴,
解得,
故一次函数的解析式为y=﹣x+1;
(2)令x=0,则y=﹣x+1=1,
∴M(0,1),
∴△AOB的面积=S△BOM+S△AOM==3;
(3)观察图象,当kx+b>时,x的取值范围是:x<﹣2或0<x<4.
故答案为:x<﹣2或0<x<4.
【点评】此题考查了反比例函数和一次函数的交点问题,解题的关键是根据所给的条件得出A、B点的坐标,求出函数的解析式.注意运用数形结合的思想,难度不大,是中考常考的题型.
55.如图,一次函数y=﹣2x+1与反比例函数的图象在第二象限交于点A,且点A的横坐标为﹣1.
(1)求反比例函数的解析式;
(2)点B的坐标是(﹣2,0),若点P在y轴上,且△AOP的面积与△AOB的面积相等,求点P的坐标.
【分析】(1)首先确定点A的坐标,再利用待定系数法求出k即可;
(2)设P(0,m),构建方程求解.
【解答】解(1)∵一次函数y=﹣2x+1与反比例函数y=的图象在第二象限交于点A,点A的横坐标为﹣1,
当x=﹣1时,y=﹣2×(﹣1)+1=3,
∴A(﹣1,3),
∴3=,
∴k=﹣3,
∴反比例函数的解析式为y=﹣;
(2)设P(0,m),
∵△AOP的面积与△AOB的面积相等,
∴×|m|×1=×2×3,
∴m=±6,
∴P(0,6)或(0,﹣6).
【点评】本题考查反比例函数的性质,一次函数的性质等知识,解题的关键是掌握待定系数法,属于中考常考题型.
56.如图1,有一块边角料ABCDE,其中AB,BC,DE,EA是线段,曲线CD可以看成反比例函数图象的一部分.小宁想利用这块边角料截取一个面积最大的矩形MNQP,其中M,N在AE上(点M在点N左侧),点P在线段BC上,点Q在曲线CD上.测量发现:∠A=∠E=90°,AE=5,AB=DE=1,点C到AB,AE所在直线的距离分别为2,4.
(1)小宁尝试建立坐标系来解决该问题,通过思考,他把A,B,C,D,E这5个点先描到平面直角坐标系上,记点A的坐标为(﹣1,0);点B的坐标为(﹣1,1).
请你在图2中补全平面直角坐标系并画出图形ABCDE;
(2)求直线BC,曲线CD的解析式;
(3)求矩形MNQP的最大面积.
【分析】(1)由题意即可如图;
(2)用待定系数法即可求解;
(3)设点P坐标为,得到点Q坐标为,进而求解.
【解答】解:(1)由题意,如图如下:
(2)设直线BC的解析式为y=kx+b(k≠0),
则,解得:,
则直线BC的解析式为:,
设曲线的表达式为:y=,
由点C(1,4)得曲线CD的解析式得:m=4×1=4,
则反比例函数的表达式为:;
(3)如图,设点M的横坐标为m,则点P坐标为,
∴.
∵四边形MNQP是矩形,
∴,
∴点Q坐标为,
设矩形MNQP的面积为S.
则,
∴当时,矩形MNQP的面积的最大值为.
【点评】本题为反比例函数综合题,涉及到一次函数的基本性质、矩形的性质、图形的面积等,有一定的综合性,难度不大.
57.如图,在平面直角坐标系xOy中,直线l:y=x+b与x轴、y轴分别交于点A、B,与双曲线H:y=交于点P(2,),直线x=m分别与直线l和双曲线H交于点E、D.
(1)求k和b的值;
(2)当点E在线段AB上时,如果ED=BO,求m的值;
(3)如果△BDE是以BE为腰的等腰三角形,求点E的坐标.
【分析】(1)利用待定系数法求出k和b的值即可;
(2)由题意得出,E(m,m+3),D(m,),DE=m+3﹣,利用DE=BO,建立方程求解即可;
(3)过点E作EF⊥y轴于点F,运用勾股定理求出BE=|m|,再根据BE=DE列方程求解,根据m的值确定E点的坐标即可.
【解答】解:(1)把点P(2,)代入y=,
得=,
解得k=9,
把点P(2,)代入y=x+b,
得+b=,
解得b=3;
(2)在直线y=x+3中,令x=0,
得y=3,
∴B(0,3),
∴OB=3,
令y=0,得x+3=0,
解得x=﹣4,
∴A(﹣4,0),
∵直线x=m,分别与直线l和双曲线H交于点E、D,
∴E(m,m+3),D(m,),
∵点E在线段AB上,
∴﹣4≤m≤0,
∴ED=m+3﹣,
∵ED=BO,
∴m+3﹣=3,
解得m=﹣2,m'=2(不符合题意,舍去),
∴m的值为﹣2;
(3)如图,过点E作EF⊥y轴于点F,
∵B(0,3),E(m,m+3),D(m,),
∴F(0,m+3),
∴BE====|m|,
又∵DE=|m+3﹣|,△BDE是以BE为腰的等腰三角形,
∴BE=DE,
即|m|=|m+3﹣|,
解得m=﹣3,m'=,
∴E(﹣3,)或(,).
【点评】本题主要考查反比例函数的综合题,熟练掌握反比例函数的图象和性质,一次函数的图形和性质,待定系数法求解析式等知识是解题的关键.
58.如图,已知直线y=x﹣2与x轴交于A点,与y轴交于B点,P(m,n)为双曲线上一动点,过P点分别作x轴,y轴的垂线,垂足分别为C,D,射线PC交直线AB于点E,射线PD交直线AB于点F.
(1)当DF=PC时,求m的值;
(2)连接OE,OF,求证:∠EOF的度数为45°;
(3)在双曲线上有一点Q(不与点P重合),连接PQ,有PQ∥AB,将线段PQ沿直线AB翻折得到线段P′Q′.若线段P′Q′与坐标轴没有交点,求此时n的取值范围.
【分析】(1)由题意得:点P(m,﹣),则点F(2﹣,﹣),得到=2﹣,即可求解;
(2)证明△OFA∽△EFO,得到∠FOE=∠FAO,即可求解;
(3)设点P′、Q′恰好坐落在x、y轴上,此时,线段P′Q′与坐标轴有交点的临界点,进而求解.
【解答】(1)解:由题意得:点P(m,﹣),则点F(2﹣,﹣),
∵DF=PC,即=2﹣,
解得:m=2;
(2)证明:∵点E、F在直线AB上,故设点E、F的坐标分别为:(m,m﹣2)、(n+2,n),
由点O、E、F的坐标得:OF2=(n+2)2+n2=2n2+4n+4,
EF==(m﹣n﹣2),AF==n,
则EF AF=(m﹣n﹣2)×n=2n2+4n+4=OF2,
∵∠OFA=∠EFO,
∴△OFA∽△EFO,
∴∠FOE=∠FAO,
由直线AB的表达式知,∠FAO=45°,
∴∠EOF的度数为45°;
(3)解:如图,设点P′、Q′恰好坐落在x、y轴上,此时,线段P′Q′与坐标轴有交点的临界点,
连接AP、BQ,
由图象的对称性知,PP′⊥AB,
则点A在PP′的中垂线上,即PA=PA′,
由AB的表达式知,∠BAP′=45°=∠BAP,
则∠PAP′=90°,则点P的横坐标为2,则点P(2,﹣1),
同理可得,点Q(1,﹣2),
此外,当n=﹣时,点P、Q重合,不符合题意,
则﹣2<n<﹣1且n≠﹣.
【点评】本题为反比例函数综合题,考查了反比例函数与一次函数的交点问题、三角形相似、勾股定理的运用等,有一定的综合性,难度适中.
59.一次函数y=﹣2x+6与反比例函数(k>0,k为常数)的图象交点为A(a,4)和点B,点C是反比例函数(k>0,k为常数)在第三象限内的图象上一点.
(1)求反比例函数的解析式和点B的坐标;
(2)若点C为直线OB与反比例函数的另一个交点,求△ACB的面积;
(3)我们将对角线相等且互相垂直的四边形称为“等直四边形”.如图2,在平面内一点D,AB∥CD,且四边形ABCD为“等直四边形”,求点C的坐标.
【分析】(1)用待定系数法即可求解;
(2)由△ACB的面积=S△ATC+S△ATB=AT (xB﹣xC),即可求解;
(3)证明△HGA≌△BNH(AAS),得到GA=HN,GH=BN,进而求解.
【解答】解:(1)将点A的坐标代入一次函数表达式得:4=﹣2a+6,则a=1,即点A(1,4),
将点A的坐标代入反比例函数表达式得:k=1×4=4,
则反比例函数的表达式为:y=①,
联立,
解得:,
即点B(2,2);
(2)根据点的对称性,点C和点B关于原点对称,则点C(﹣2,﹣2),
由题意得,直线BC的表达式为:y=x,
过点A作AT∥y轴于点T,则点T(1, 1),则AT=4﹣1=3,
则△ACB的面积=S△ATC+S△ATB=AT (xB﹣xC)=×(2+2)=6;
(3)设AC和BD交于点H,
根据“等直四边形”的定义,AC⊥BD,则∠AHB=90°,且AC=BD,
根据图象的对称性,△ABH为等腰直角三角形,且AH=BH,
如图,将左侧图部分放大,设点H(m,n),
过点H作GN∥y轴,交过点A和x轴的平行线于点G,交过点B与x轴的平行线于点N,
∵∠GHA+∠GAH=90°,∠GHA+∠BHN=90°,
∴∠GAH=∠BHN,
∵∠HGA=∠BNH=90°,AH=BH,
∴△HGA≌△BNH(AAS),
则GA=HN,GH=BN,
即n﹣2=1﹣m且4﹣n=2﹣m,
解得:,
则点H(,),
由点A、H的坐标得,直线AH的表达式为:y=3x+1②,
联立①②得:=3x+1,
解得:x=1(舍去)或﹣,
即点C(﹣,﹣3).
【点评】本题为反比例函数综合运用题,涉及到新定义、面积的计算、一次函数的性质等,正确理解新定义是本题解题的关键.
60.一、问题背景:
数学活动课上,老师拿出一个由五连格边长为1的正方形连成的L形教具,将它放入一个的直角三角形中,
∠BCA=90°,∠B=30°,如图1顶点D,E,F,G刚好落在三边上,请求出此直角三角形的面积.
二、问题提出与解决:(以下问题二选一解答)
(1)小颖同学受到启发,将此教具放入如图的直角坐标系中,顶点A,B,C分别落在坐标轴上,提出问题:如图2,如果反比例函数图象经过顶点D,试求出反比例解析式.
(2)小明同学也受到启发,画了一个圆,如图3,将此教具放入圆内,使圆经过其顶点A,B,C,提出问题:怎么算出圆的面积?
【分析】(一)如图1,由题意知GD=2,GF=4,GF∥AB,∠B=30°,则∠CFG=∠B=30°,求出AG,AC,BC的值,再根据直角三角形的面积公式计算即可;
(二)(1)如图2,过D作DE⊥x轴于E,由题意知,AB=1,AD=4,CF=1,BF=3,∠DAB=∠ABF=∠CFB=∠AOB=∠DEA=90°,然后由△BAO∽△CBF和△ADE∽△BAO求出AO,BO,AE,DE,从而得出D坐标,代入反比例函数解析式求k,进而可得反比例函数解析式;
(2)如图3,取AB中点E,作EF⊥FC,取圆心O,连接OB,OC,则OB=OC,由正方形的性质CF=,BE=,EF=4,设OF=x,OE=4﹣x,在Rt△COF和Rt△BOE中,由勾股定理得关于x的方程,解方程求x的值,OC的值,进而可得⊙O的半径,然后代入圆的面积公式进行求解即可.
【解答】解:一、问题背景:
如图所示:
由题意知GD=2,GF=4,GF∥AB,∠B=30°,
∴∠CFG=∠B=30°,∠A=60°,
∴CG=GF=2,AG==,
∴AC=+2,BC=AC tan60°=4+2,
∴S△ABC=AC BC=×(+2)×(4+2)=+8,
∴此直角三角形的面积为+8;
二、问题提出与解决:
(1)如图所示:过D作DE⊥x轴于E,
由题意知,AB=1.AD=4,CF=1,BF=3,∠DAB=∠ABF=∠CFB=∠AOB=∠DEA=90°,
在Rt△BCF中,由勾股定理得BC==,
∵∠ABO+∠BAO=∠ABO+∠CBF,
∴∠BAO=∠CBF,
∴△BAO∽△CBF,
∴,即,
解得AO=,BO=,
同理△ADE∽△BAO,
∴,
即==,
解得AE=,DE=,
∴OE=AO+AE=,
∴D(﹣,),
∴k=xy=﹣×=﹣,
∴反比例函数解析式为y=﹣;
(2)如图,取AB中点E,作EF⊥FC,取圆心O,连接OB,OC,则OB=OC,
由正方形的性质CF=,BE=,EF=4,
设OF=x,OE=4﹣x,
在Rt△COF中,由勾股定理得:OC2=CF2+OF2=()2+x2,
在Rt△BOE中,由勾股定理得:OB2=BE2+OE2=()2+(4﹣x)2,
∴()2+x2=()2+(4﹣x)2,
解得x=,
∴OC=,
∴⊙O的半径为,
∴圆O的面积=πr2=π×()2=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
