第二章简单事件的概率单元测试
图片预览



文档简介
第2章简单事件的概率单元测试卷
(100分,90分钟)
一、选择题(每题3分,共30分)
1.从2,-2,1,-1四个数中任取两个数求和,其和为0的概率是( )
A. B. C. D.
2.关于频率和概率的关系,下列说法正确的是( )
A.频率等于概率
B.当试验次数很大时,频率稳定在概率附近
C.当试验次数很大时,概率稳定在频率附近
D.试验得到的频率与概率不可能相等
3.从某班学生中随机选取一名学生是女生的概率为,则该班女生与男生的人数比是( )
A. B. C. D.
4.在一个不透明的布袋中装有50个黄、白两种颜色的球,这些球除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.3左右,则布袋中白球可能有( )【来源:21·世纪·教育·网】
A.15个 B.20个
C.30个 D.35个
5.某火车站的显示屏每间隔4分钟显示一次火车班次的信息,显示时间持续1分钟,某人到达该车站时,显示屏上正好显示火车班次信息的概率是( )2·1·c·n·j·y
A. B. C. D.
6.一个布袋里装有只有颜色不同的5个球,其中3个红球,2个白球.从中任意摸出1个球,记下颜色后放回,搅匀,再任意摸出1个球.摸出的2个球都是红球的概率是( )
A. B. C. D.
7.做“抢30”的游戏时,如果将游戏规则中“不可以连说三个数,谁先抢到30,谁就获胜.”改为“每次最多可以连说三个数,谁先抢到33,谁就获胜.”那么采取适当策略,其结果是( )
A.先说数者胜B.后说数者胜
C.两者都能胜D.无法判断
8.某班共有41名同学,其中有2名同学习惯用左手写字,其余同学都习惯用右手写字,老师随机请1名同学解答问题,习惯用左手写字的同学被选中的概率是( )【出处:21教育名师】
A.0 B. C. D.1
9.现有A,B两枚均匀的小立方体,小立方体的每个面上分别标有数字1,2,3,4,5,6.用小刚掷A立方体朝上的数字x,小明掷B立方体朝上的数字y来确定点P(x,y),那么他们各掷一次所确定的点P落在抛物线y=-x2+4x上的概率为( )
A. B. C. D.
10.(2013,连云港)在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一球,记下颜色……如此大量的摸球试验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%.对此试验,他总结出下列结论:①若进行大量的摸球试验,摸出白球的频率应稳定于30%;②若从布袋中随机摸出一球,该球是黑球的概率最大;③若再摸球100次,必有20次摸出的是红球.其中说法正确的是( )
A.①②③ B.①②
C.①③ D.②③
二、填空题(每题3分,共18分)
11.“明天下雨的概率为0.99”则“明天下雨”是 ________事件.
12.从数字1,2,3中任取两个不同数字组成一个两位数,则这个两位数大于21的概率是________.21教育网
13.在一个不透明的布袋中装有2个白球和n个黄球,它们除颜色不同外其余均相同.若从中随机摸出一个球,摸到黄球的概率是,则n=_____.21·世纪*教育网
14.一个不透明的口袋里有10个黑球和若干个黄球,从口袋中随机摸出一球记下其颜色,再把它放回口袋中摇匀,重复上述过程,共试验200次,其中有120次摸到黄球,由此估计袋中的黄球有_______个.
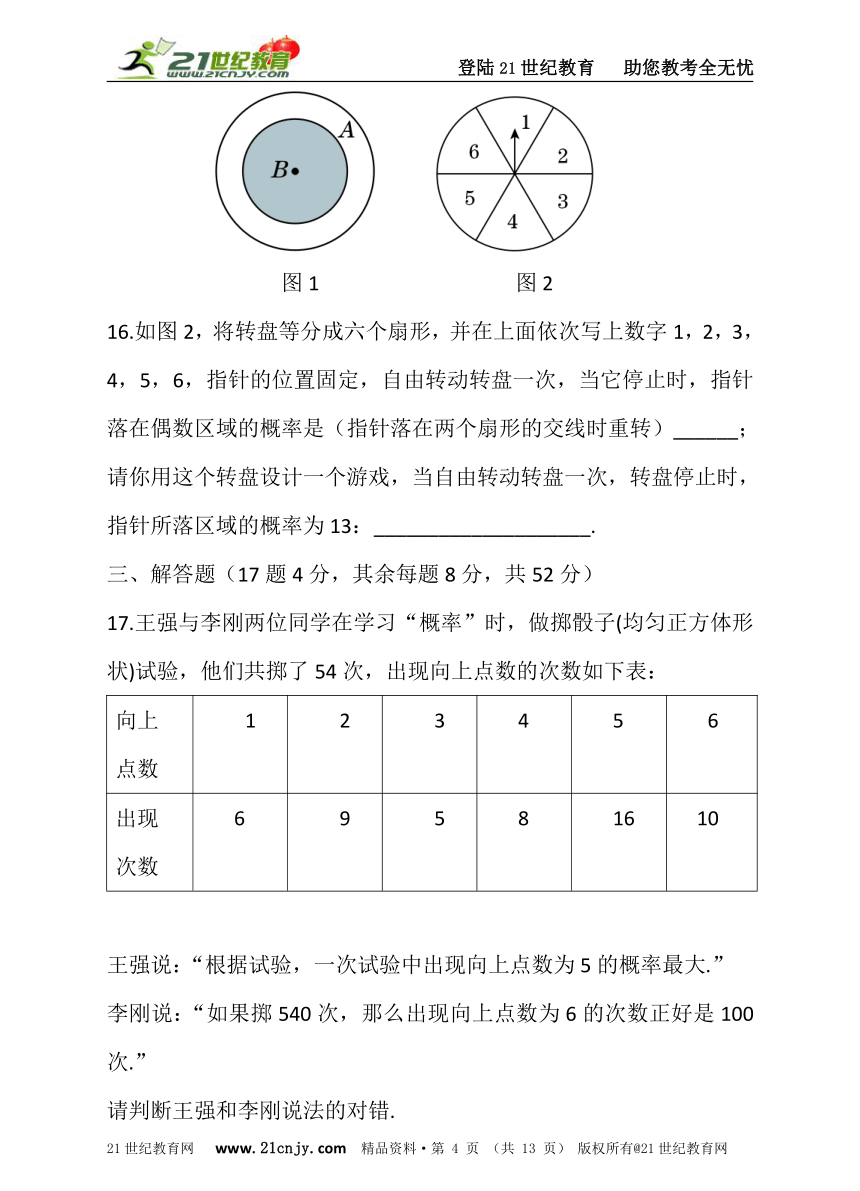
15.2013年1月11日,云南省昭通市镇雄县果珠乡高坡村赵家沟村民组发生山体滑坡,造成重大人员伤亡,需要空投救灾物资到指定的区域(⊙A),如图1所示,若空投救灾物资落在中心区域(⊙B)的概率为, 则⊙B与⊙A的半径之比为_______.
图1 图2
16.如图2,将转盘等分成六个扇形,并在上面依次写上数字1,2,3,4,5,6,指针的位置固定,自由转动转盘一次,当它停止时,指针落在偶数区域的概率是(指针落在两个扇形的交线时重转)______;请你用这个转盘设计一个游戏,当自由转动转盘一次,转盘停止时,指针所落区域的概率为13:____________________.
三、解答题(17题4分,其余每题8分,共52分)
17.王强与李刚两位同学在学习“概率”时,做掷骰子(均匀正方体形状)试验,他们共掷了54次,出现向上点数的次数如下表:
向上
点数
1
2
3
4
5
6
出现
次数
6
9
5
8
16
10
王强说:“根据试验,一次试验中出现向上点数为5的概率最大.”
李刚说:“如果掷540次,那么出现向上点数为6的次数正好是100次.”
请判断王强和李刚说法的对错.
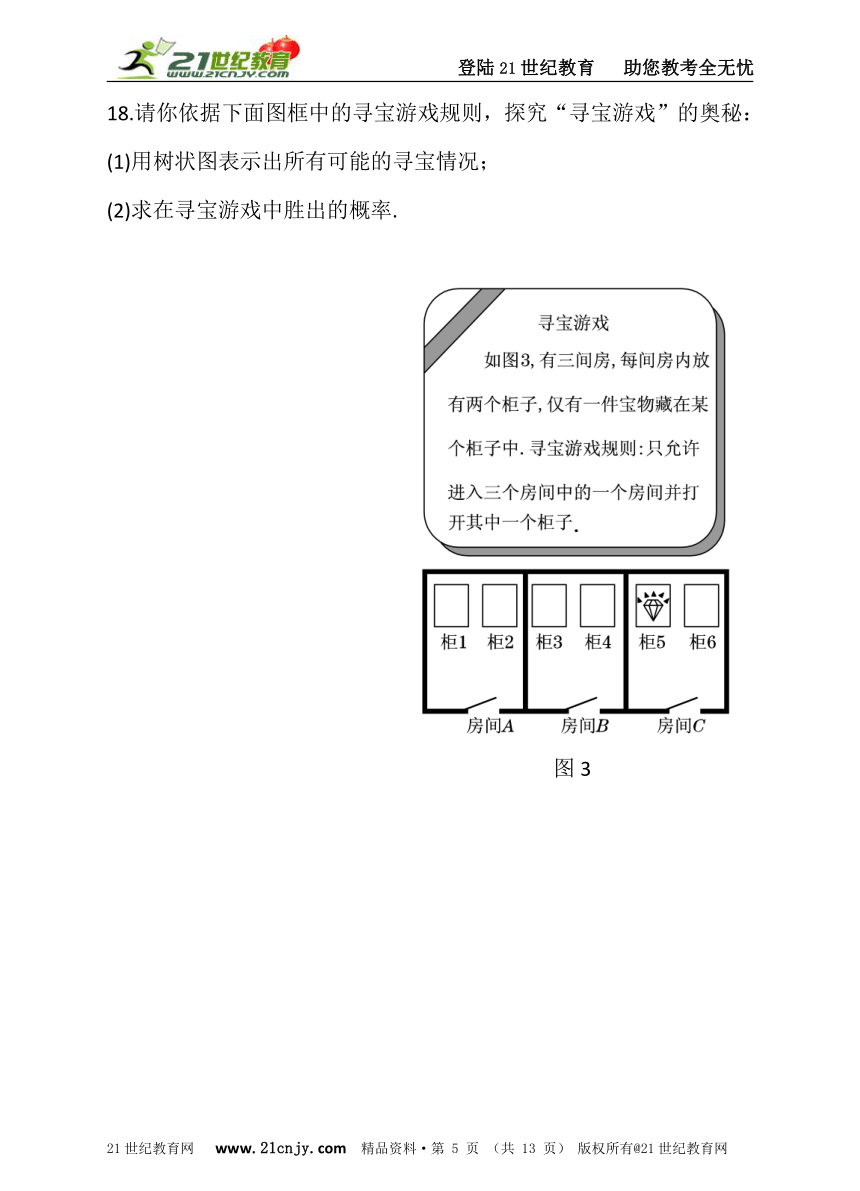
18.请你依据下面图框中的寻宝游戏规则,探究“寻宝游戏”的奥秘:
(1)用树状图表示出所有可能的寻宝情况;
(2)求在寻宝游戏中胜出的概率.
图3
19.某商场为了吸引顾客,设计了一个摸球获奖的箱子,箱子中共有20个球,其中红球2个,蓝球3个,黄球5个,白球10个,并规定每购买100元的商品,就有一次摸球的机会,摸到红、蓝、黄、白球的(一次只能摸一个)顾客就可以分别得到80元、30元、10元、0元购物券,凭购物券仍然可以在商场购买商品,如果顾客不愿意摸球,那么可以直接获得购物券10元.21世纪教育网版权所有
(1)每摸一次球所获购物券金额的平均值是多少?
(2)你若在此商场购买100元的商品,两种获得购物券的方式中你应选择哪种方式?为什么?
20.某商场设立了一个可以自由转动的转盘(如图4),并规定:顾客购买10元以上的商品就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据: 21·cn·jy·com
转动转盘的次数n
100
150
200
500
800
1 000
落在“铅笔”区域的次数m
68
111
136
346
564
701
落在“铅笔”区域的频率
(1)计算并完成表格;
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角的度数大约是多少?
图4
21.如图5,有A、B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,6,8这6个数字.同时转动两个转盘各一次(指针落在等分线上时重转),转盘自由停止后,A转盘中指针指向的数字记为x,B转盘中指针指向的数字记为y,点Q的坐标记为(x,y).21cnjy.com
(1)用列表法或树状图表示(x,y)所有可能出现的结果;
(2)求出点Q(x,y)落在第四象限的概率.
图5
22.瑶瑶在操场上玩耍,她发现地上有一个不规则的封闭图形ABC(如图6所示),为了求其面积,瑶瑶在封闭的图形中画了一个半径为1 m的圆,在不远处向封闭图形ABC内掷石子,且记录如下:
掷石子次数
50
150
300
石子落在⊙O内(含⊙O上)的次数m
14
43
93
石子落在阴影内的次数n
29
85
186
图6
你能否求出封闭图形ABC的面积?试试看.
23.(2013,连云港)甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.2-1-c-n-j-y
(1)若开始时球在甲手中,求经过三次传球后,球传回甲手中的概率是多少?
(2)若乙想使球经过三次传递后,球落在自己手中的概率最大,乙会让球开始时在谁手中?请说明理由.
参考答案及点拨
一、1.C点拨:从2,-2,1,-1四个数中任取两个数求和共有六种情况,即2+(-2),2+1,2+(-1),(-2)+1,(-2)+(-1),1+(-1),而和为0的情况有两种,所以所求概率P==.所以选C.www-2-1-cnjy-com
2.B
3.A点拨:由题意可知,从该班随机选取一名学生是男生的概率是,则该班女生与男生的人数比是.
4.D 5.B 6.D 7.A 8.C
9.B点拨:点P的坐标共有36种可能,其中能落在抛物线y=-x2+4x上的共有3种可能,其概率为=,所以选B. 21*cnjy*com
10.B
二、11.随机
12. 点拨:从1,2,3中任取两个不同数字组成一个两位数,有6种等可能的结果,其中大于21的有3种:23,31,32.所以P(组成的两位数大于21)==.
13.8 14.15
15.∶2点拨:设⊙A的半径为R,⊙B的半径为r,则⊙A的面积为πR2,⊙B的面积为πr2,由已知得=,得r∶R=∶2.【来源:21cnj*y.co*m】
16. ;自由转动转盘一次,当转盘停止时,指针落在大于4的数字所在的区域
点拨:第2个空答案不唯一.
三、17.解:因为掷一次骰子出现点数1,2,3,4,5,6向上具有等可能性,所以出现每个点数向上的概率都是,所以王强的说法不对;虽然题中掷54次出现点数6向上的频率是,但频率不一定等于概率.因为掷一次骰子,点数6向上的概率是,所以李刚的说法也是不正确的.【版权所有:21教育】
点拨:本题是易错题,易混淆频率和概率而出错. 二者虽有联系,但不能简单地等同.概率是个定值,而频率随不同试验次数而有所不同,当试验次数足够大时,频率是概率的近似值.题目中的试验次数只有54次,未达到使频率值稳定的试验次数,故用其频率来估计概率是错误的;另外,即使出现向上点数为6的概率为,也不能保证掷540次,出现向上点数为6的次数正好是100次.21教育名师原创作品
18.解:(1)树状图如答图1所示.
答图1
(2)由答图1中的树状图可知:P(胜出)=.
19.解:(1) ∵P(摸到红球)=,P(摸到蓝球)=,
P(摸到黄球) =,P(摸到白球)=,∴每摸一次球所获购物券金额的平均值是80×+30×+10×=15(元).
(2)∵15>10,∴两种获得购物券的方式中我会选择摸球这种方式,这样较合算.
20.解:(1)表中的数据从左至右依次填:0.68,0.74,0.68,0.692,0.705,0.701.(2)当n很大时,频率将会接近0.7.(3)获得铅笔的概率约是0.7.(4)表示“铅笔”区域的扇形的圆心角的度数大约是0.7×360°=252°.www.21-cn-jy.com
点拨:本题综合考查了频数与频率以及用频率估计概率的知识,解答时应灵活运用这些知识.
21.解:(1)列表如下:
B(y)
Q(x,y)
A(x)
-4
6
8
-1
(-1,-4)
(-1,6)
(-1,8)
2
(2,-4)
(2,6)
(2,8)
3
(3,-4)
(3,6)
(3,8)
(2)由(1)中的表格可知:点Q出现的所有可能结果有9种,位于第四象限的结果有2种,∴点Q(x,y)落在第四象限的概率为 21*cnjy*com
22.解:由记录可知稳定在,所以P(落在⊙O内)≈,又P(落在⊙O内)=,所以≈13,又因为S⊙O=π·12=π(m2),所以S图形ABC≈3π(m2).
23.解:(1)画树状图如答图2,三次传球有8种等可能结果,其中传回甲手中的有2种.所以P(传球三次回到甲手中)==.
(2)乙会让球开始时在甲手中或丙手中.理由:由(1)可知:从甲开始传球,传球三次后球传到甲手中的概率为,球传到乙、丙手中的概率均为,所以三次传球后球回到乙手中概率最大值为.
所以乙会让球开始时在甲手中或丙手中.
答图2
(100分,90分钟)
一、选择题(每题3分,共30分)
1.从2,-2,1,-1四个数中任取两个数求和,其和为0的概率是( )
A. B. C. D.
2.关于频率和概率的关系,下列说法正确的是( )
A.频率等于概率
B.当试验次数很大时,频率稳定在概率附近
C.当试验次数很大时,概率稳定在频率附近
D.试验得到的频率与概率不可能相等
3.从某班学生中随机选取一名学生是女生的概率为,则该班女生与男生的人数比是( )
A. B. C. D.
4.在一个不透明的布袋中装有50个黄、白两种颜色的球,这些球除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.3左右,则布袋中白球可能有( )【来源:21·世纪·教育·网】
A.15个 B.20个
C.30个 D.35个
5.某火车站的显示屏每间隔4分钟显示一次火车班次的信息,显示时间持续1分钟,某人到达该车站时,显示屏上正好显示火车班次信息的概率是( )2·1·c·n·j·y
A. B. C. D.
6.一个布袋里装有只有颜色不同的5个球,其中3个红球,2个白球.从中任意摸出1个球,记下颜色后放回,搅匀,再任意摸出1个球.摸出的2个球都是红球的概率是( )
A. B. C. D.
7.做“抢30”的游戏时,如果将游戏规则中“不可以连说三个数,谁先抢到30,谁就获胜.”改为“每次最多可以连说三个数,谁先抢到33,谁就获胜.”那么采取适当策略,其结果是( )
A.先说数者胜B.后说数者胜
C.两者都能胜D.无法判断
8.某班共有41名同学,其中有2名同学习惯用左手写字,其余同学都习惯用右手写字,老师随机请1名同学解答问题,习惯用左手写字的同学被选中的概率是( )【出处:21教育名师】
A.0 B. C. D.1
9.现有A,B两枚均匀的小立方体,小立方体的每个面上分别标有数字1,2,3,4,5,6.用小刚掷A立方体朝上的数字x,小明掷B立方体朝上的数字y来确定点P(x,y),那么他们各掷一次所确定的点P落在抛物线y=-x2+4x上的概率为( )
A. B. C. D.
10.(2013,连云港)在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一球,记下颜色……如此大量的摸球试验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%.对此试验,他总结出下列结论:①若进行大量的摸球试验,摸出白球的频率应稳定于30%;②若从布袋中随机摸出一球,该球是黑球的概率最大;③若再摸球100次,必有20次摸出的是红球.其中说法正确的是( )
A.①②③ B.①②
C.①③ D.②③
二、填空题(每题3分,共18分)
11.“明天下雨的概率为0.99”则“明天下雨”是 ________事件.
12.从数字1,2,3中任取两个不同数字组成一个两位数,则这个两位数大于21的概率是________.21教育网
13.在一个不透明的布袋中装有2个白球和n个黄球,它们除颜色不同外其余均相同.若从中随机摸出一个球,摸到黄球的概率是,则n=_____.21·世纪*教育网
14.一个不透明的口袋里有10个黑球和若干个黄球,从口袋中随机摸出一球记下其颜色,再把它放回口袋中摇匀,重复上述过程,共试验200次,其中有120次摸到黄球,由此估计袋中的黄球有_______个.
15.2013年1月11日,云南省昭通市镇雄县果珠乡高坡村赵家沟村民组发生山体滑坡,造成重大人员伤亡,需要空投救灾物资到指定的区域(⊙A),如图1所示,若空投救灾物资落在中心区域(⊙B)的概率为, 则⊙B与⊙A的半径之比为_______.
图1 图2
16.如图2,将转盘等分成六个扇形,并在上面依次写上数字1,2,3,4,5,6,指针的位置固定,自由转动转盘一次,当它停止时,指针落在偶数区域的概率是(指针落在两个扇形的交线时重转)______;请你用这个转盘设计一个游戏,当自由转动转盘一次,转盘停止时,指针所落区域的概率为13:____________________.
三、解答题(17题4分,其余每题8分,共52分)
17.王强与李刚两位同学在学习“概率”时,做掷骰子(均匀正方体形状)试验,他们共掷了54次,出现向上点数的次数如下表:
向上
点数
1
2
3
4
5
6
出现
次数
6
9
5
8
16
10
王强说:“根据试验,一次试验中出现向上点数为5的概率最大.”
李刚说:“如果掷540次,那么出现向上点数为6的次数正好是100次.”
请判断王强和李刚说法的对错.
18.请你依据下面图框中的寻宝游戏规则,探究“寻宝游戏”的奥秘:
(1)用树状图表示出所有可能的寻宝情况;
(2)求在寻宝游戏中胜出的概率.
图3
19.某商场为了吸引顾客,设计了一个摸球获奖的箱子,箱子中共有20个球,其中红球2个,蓝球3个,黄球5个,白球10个,并规定每购买100元的商品,就有一次摸球的机会,摸到红、蓝、黄、白球的(一次只能摸一个)顾客就可以分别得到80元、30元、10元、0元购物券,凭购物券仍然可以在商场购买商品,如果顾客不愿意摸球,那么可以直接获得购物券10元.21世纪教育网版权所有
(1)每摸一次球所获购物券金额的平均值是多少?
(2)你若在此商场购买100元的商品,两种获得购物券的方式中你应选择哪种方式?为什么?
20.某商场设立了一个可以自由转动的转盘(如图4),并规定:顾客购买10元以上的商品就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据: 21·cn·jy·com
转动转盘的次数n
100
150
200
500
800
1 000
落在“铅笔”区域的次数m
68
111
136
346
564
701
落在“铅笔”区域的频率
(1)计算并完成表格;
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角的度数大约是多少?
图4
21.如图5,有A、B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,6,8这6个数字.同时转动两个转盘各一次(指针落在等分线上时重转),转盘自由停止后,A转盘中指针指向的数字记为x,B转盘中指针指向的数字记为y,点Q的坐标记为(x,y).21cnjy.com
(1)用列表法或树状图表示(x,y)所有可能出现的结果;
(2)求出点Q(x,y)落在第四象限的概率.
图5
22.瑶瑶在操场上玩耍,她发现地上有一个不规则的封闭图形ABC(如图6所示),为了求其面积,瑶瑶在封闭的图形中画了一个半径为1 m的圆,在不远处向封闭图形ABC内掷石子,且记录如下:
掷石子次数
50
150
300
石子落在⊙O内(含⊙O上)的次数m
14
43
93
石子落在阴影内的次数n
29
85
186
图6
你能否求出封闭图形ABC的面积?试试看.
23.(2013,连云港)甲、乙、丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,共传球三次.2-1-c-n-j-y
(1)若开始时球在甲手中,求经过三次传球后,球传回甲手中的概率是多少?
(2)若乙想使球经过三次传递后,球落在自己手中的概率最大,乙会让球开始时在谁手中?请说明理由.
参考答案及点拨
一、1.C点拨:从2,-2,1,-1四个数中任取两个数求和共有六种情况,即2+(-2),2+1,2+(-1),(-2)+1,(-2)+(-1),1+(-1),而和为0的情况有两种,所以所求概率P==.所以选C.www-2-1-cnjy-com
2.B
3.A点拨:由题意可知,从该班随机选取一名学生是男生的概率是,则该班女生与男生的人数比是.
4.D 5.B 6.D 7.A 8.C
9.B点拨:点P的坐标共有36种可能,其中能落在抛物线y=-x2+4x上的共有3种可能,其概率为=,所以选B. 21*cnjy*com
10.B
二、11.随机
12. 点拨:从1,2,3中任取两个不同数字组成一个两位数,有6种等可能的结果,其中大于21的有3种:23,31,32.所以P(组成的两位数大于21)==.
13.8 14.15
15.∶2点拨:设⊙A的半径为R,⊙B的半径为r,则⊙A的面积为πR2,⊙B的面积为πr2,由已知得=,得r∶R=∶2.【来源:21cnj*y.co*m】
16. ;自由转动转盘一次,当转盘停止时,指针落在大于4的数字所在的区域
点拨:第2个空答案不唯一.
三、17.解:因为掷一次骰子出现点数1,2,3,4,5,6向上具有等可能性,所以出现每个点数向上的概率都是,所以王强的说法不对;虽然题中掷54次出现点数6向上的频率是,但频率不一定等于概率.因为掷一次骰子,点数6向上的概率是,所以李刚的说法也是不正确的.【版权所有:21教育】
点拨:本题是易错题,易混淆频率和概率而出错. 二者虽有联系,但不能简单地等同.概率是个定值,而频率随不同试验次数而有所不同,当试验次数足够大时,频率是概率的近似值.题目中的试验次数只有54次,未达到使频率值稳定的试验次数,故用其频率来估计概率是错误的;另外,即使出现向上点数为6的概率为,也不能保证掷540次,出现向上点数为6的次数正好是100次.21教育名师原创作品
18.解:(1)树状图如答图1所示.
答图1
(2)由答图1中的树状图可知:P(胜出)=.
19.解:(1) ∵P(摸到红球)=,P(摸到蓝球)=,
P(摸到黄球) =,P(摸到白球)=,∴每摸一次球所获购物券金额的平均值是80×+30×+10×=15(元).
(2)∵15>10,∴两种获得购物券的方式中我会选择摸球这种方式,这样较合算.
20.解:(1)表中的数据从左至右依次填:0.68,0.74,0.68,0.692,0.705,0.701.(2)当n很大时,频率将会接近0.7.(3)获得铅笔的概率约是0.7.(4)表示“铅笔”区域的扇形的圆心角的度数大约是0.7×360°=252°.www.21-cn-jy.com
点拨:本题综合考查了频数与频率以及用频率估计概率的知识,解答时应灵活运用这些知识.
21.解:(1)列表如下:
B(y)
Q(x,y)
A(x)
-4
6
8
-1
(-1,-4)
(-1,6)
(-1,8)
2
(2,-4)
(2,6)
(2,8)
3
(3,-4)
(3,6)
(3,8)
(2)由(1)中的表格可知:点Q出现的所有可能结果有9种,位于第四象限的结果有2种,∴点Q(x,y)落在第四象限的概率为 21*cnjy*com
22.解:由记录可知稳定在,所以P(落在⊙O内)≈,又P(落在⊙O内)=,所以≈13,又因为S⊙O=π·12=π(m2),所以S图形ABC≈3π(m2).
23.解:(1)画树状图如答图2,三次传球有8种等可能结果,其中传回甲手中的有2种.所以P(传球三次回到甲手中)==.
(2)乙会让球开始时在甲手中或丙手中.理由:由(1)可知:从甲开始传球,传球三次后球传到甲手中的概率为,球传到乙、丙手中的概率均为,所以三次传球后球回到乙手中概率最大值为.
所以乙会让球开始时在甲手中或丙手中.
答图2
同课章节目录
