1.2 二次函数的图像 (1)课件(共19张PPT)
文档属性
| 名称 | 1.2 二次函数的图像 (1)课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 14:59:46 | ||
图片预览



文档简介
(共19张PPT)
1.2 二次函数的图像 (1)
浙教版九年级上册
新知导入
正比例函数y=kx(k ≠ 0),其图象是一条经过原点的直线。
一次函数y=kx+b(k ≠ 0),其图象也是一条直线。
反比例函数 (k ≠ 0),其图象是双曲线。
y=
最简单的二次函数:
y=x2,
其图像是什么?
三步:列表、描点,连线
x
0
y
x
0
y
x
0
y
x
0
y
x
0
y
y=kx (k>0,b=0)
y=kx (k<0)
y=kx+b (k>0,b<0)
y=kx+b (k>0,b>0)
y=kx+b (k<0,b>0)
y=kx+b (k<0,b<0)
y=
y=
新知导入
x
y
0
0
1
1
-1
1
2
4
-2
4
3
9
-3
9
3.5
12.25
-3.5
12.25
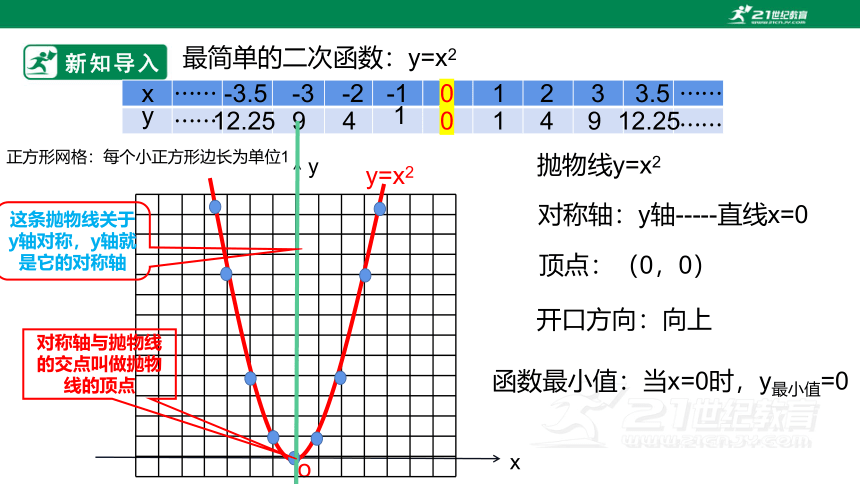
最简单的二次函数:y=x2
x
y
o
y=x2
对称轴:y轴-----直线x=0
抛物线y=x2
顶点:(0,0)
开口方向:向上
函数最小值:当x=0时,y最小值=0
对称轴与抛物线的交点叫做抛物线的顶点
这条抛物线关于y轴对称,y轴就是它的对称轴
正方形网格:每个小正方形边长为单位1
新知导入
x
y
0
0
1
-1
-1
-1
2
-4
-2
-4
3
-9
-3
-9
3.5
-12.25
-3.5
-12.25
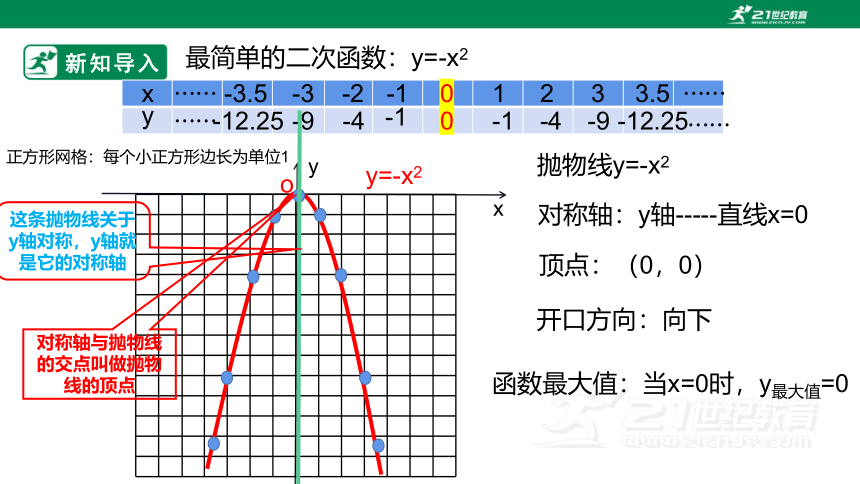
最简单的二次函数:y=-x2
x
y
o
y=-x2
对称轴:y轴-----直线x=0
抛物线y=-x2
顶点:(0,0)
开口方向:向下
函数最大值:当x=0时,y最大值=0
正方形网格:每个小正方形边长为单位1
这条抛物线关于y轴对称,y轴就是它的对称轴
对称轴与抛物线的交点叫做抛物线的顶点
抛物线
顶点坐标
对称轴
位置
开口方向
极值
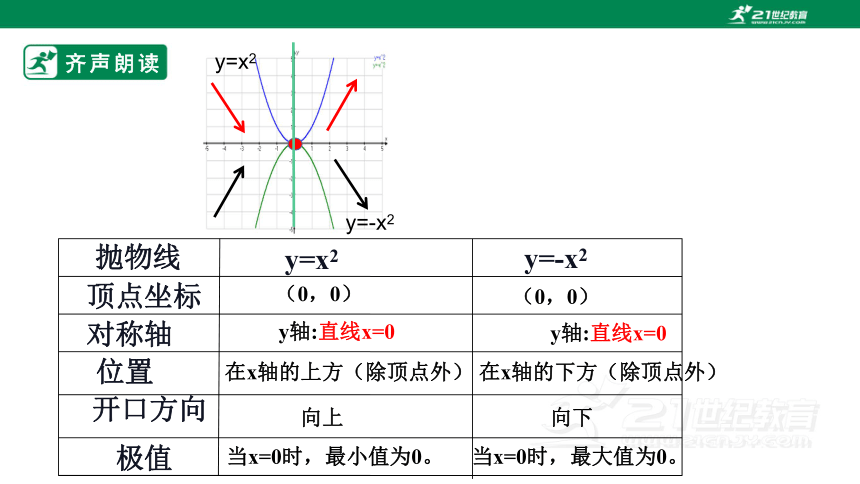
齐声朗读
y=x2
y=-x2
(0,0)
(0,0)
y轴:直线x=0
y轴:直线x=0
在x轴的上方(除顶点外)
在x轴的下方(除顶点外)
向上
向下
当x=0时,最小值为0。
当x=0时,最大值为0。
y=x2
y=-x2
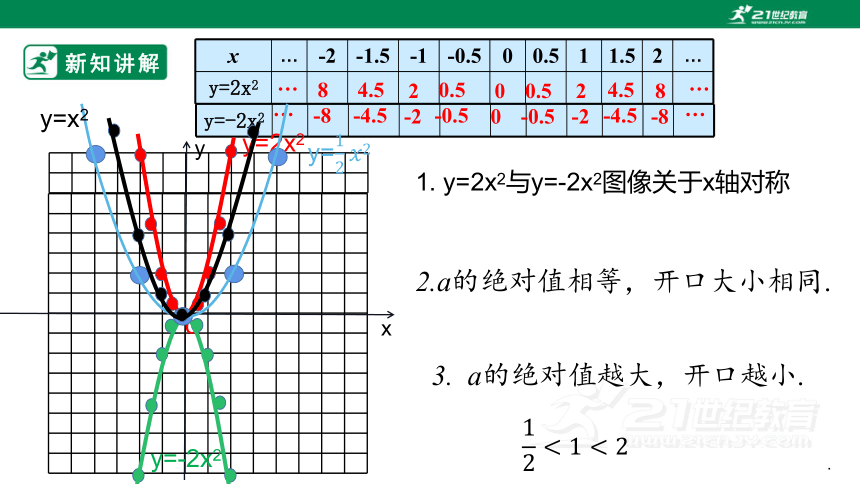
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=2x2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
y=-2x2
-8
…
-2
-0.5
0
-0.5
-2
-4.5
-8
…
-4.5
x
y
o
y=2x2
y=
.
3. a的绝对值越大,开口越小.
新知讲解
y=-2x2
1. y=2x2与y=-2x2图像关于x轴对称
y=x2
2.a的绝对值相等,开口大小相同.
y=ax2 a>0 a<0
图象
位置、开
口方向
对称性
顶点、最值
增减性
y
O
x
开口向上,在x轴上方.
y
O
x
开口向下,在x轴下方.
a的绝对值越大,开口越小.
关于y轴对称,对称轴是直线x=0.
顶点坐标是(0,0).
当x=0时,y最小值=0.
当x=0时,y最大值=0.
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
已知二次函数y=ax2(a≠0)的图像经过点(-2,-3).
(1)求a的值,并写出这个二次函数的解析式.
(2)说出这个二次函数的顶点坐标、对称轴、开口方向和图像的位置.
解:(1)把点(-2,-3)的坐标代入,得-3=,解得:a=-
这个二次函数的表达式是
(2)顶点为(0,0),对称轴为y轴,即直线x=0
因为a=-,所以这个二次函数图象的开口向下,顶点是图象上的最高点,图象在x轴的下方(除顶点外)。
新知讲解
新知讲解
y
O
x
抛物线y=ax2具有以下特征:
(1)开口方向由a的符号确定:
(3)对称轴是y轴,即直线x=0
(4)顶点坐标是(0,0),
当a>0时,(0,0)是最低点;当a<0时,(0,0)是最高点.
当a>0时,抛物线的开口向上。
当a<0时,抛物线的开口向下。
1分钟背诵
y=2x2
y=- x2
y=x2
y=-x2
(2)开口大小由|a| 的决定:
|a|越大,抛物线的开口越小;
|a|的绝对值相等,开口大小相同.
夯实基础,稳扎稳打
B
2.若抛物线y=ax2 (a ≠ 0),过点(-1,3)。
(1)则a的值是
(2)对称轴是 ,开口 。
(3)顶点坐标是 ,顶点是抛物线上的 。
抛物线在x轴的 方(除顶点外)。
3
y轴,即直线x=0
向上
(0,0)
最低点
上
y
O
x
3.若抛物线y=ax2 (a ≠ 0),过点(-1,-1)。
(1)则a的值是
(2)对称轴是 ,开口 。
(3)顶点坐标是 ,顶点是抛物线上的 。
抛物线在x轴的 方(除顶点外)。
-1
y轴,即直线x=0
向下
(0,0)
最高点
下
y
O
x
连续递推,豁然开朗
4.已知抛物线y=ax2经过点A(-2,-8).
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上.
(3)求出此抛物线上纵坐标为-6的点的坐标.
解(1)把(-2,-8)代入y=ax2,得:-8=a(-2)2, 4a=-8, a= -2,
所求函数解析式为 y= -2x2.
(2)当x=-1时,y=-2×(-1)2=-2≠-4,
所以点B(-1,-4)不在此抛物线上,
(3)由-6=-2x2 ,得x2=3, x=
所以纵坐标为-6的点有两个,它们分别是 ( ,-6), (- ,-6)
.
水平线y=-6
y=-2x2
纵坐标相同: 对称点
5.已知函数y=ax2与y=
.
x
0
y
y=
P
抛物线的开口向下
a<0
(2)抛物线开口向下,即m+3<0,所以m<-3,即m=-4
(3)抛物线有最低点,开口向上,即m+3>0,所以m>-3,即m=1
顶点坐标为(0,0),对称轴是y轴。
6、已知函数的图象是抛物线
(1)求m的值;
(2)当m为何值时,抛物线的开口向下?
(3)当m为何值时,抛物线有最低点?并写出它的顶点坐标和对称轴。
.
解:(1)因为函数是抛物线,所以此函数是二次函数
即:且m+3≠0
解得:m=-4,m=1
.
思维拓展,更上一层
7.如图,四边形OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,求a的值.
D
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.2 二次函数的图像 (1)
浙教版九年级上册
新知导入
正比例函数y=kx(k ≠ 0),其图象是一条经过原点的直线。
一次函数y=kx+b(k ≠ 0),其图象也是一条直线。
反比例函数 (k ≠ 0),其图象是双曲线。
y=
最简单的二次函数:
y=x2,
其图像是什么?
三步:列表、描点,连线
x
0
y
x
0
y
x
0
y
x
0
y
x
0
y
y=kx (k>0,b=0)
y=kx (k<0)
y=kx+b (k>0,b<0)
y=kx+b (k>0,b>0)
y=kx+b (k<0,b>0)
y=kx+b (k<0,b<0)
y=
y=
新知导入
x
y
0
0
1
1
-1
1
2
4
-2
4
3
9
-3
9
3.5
12.25
-3.5
12.25
最简单的二次函数:y=x2
x
y
o
y=x2
对称轴:y轴-----直线x=0
抛物线y=x2
顶点:(0,0)
开口方向:向上
函数最小值:当x=0时,y最小值=0
对称轴与抛物线的交点叫做抛物线的顶点
这条抛物线关于y轴对称,y轴就是它的对称轴
正方形网格:每个小正方形边长为单位1
新知导入
x
y
0
0
1
-1
-1
-1
2
-4
-2
-4
3
-9
-3
-9
3.5
-12.25
-3.5
-12.25
最简单的二次函数:y=-x2
x
y
o
y=-x2
对称轴:y轴-----直线x=0
抛物线y=-x2
顶点:(0,0)
开口方向:向下
函数最大值:当x=0时,y最大值=0
正方形网格:每个小正方形边长为单位1
这条抛物线关于y轴对称,y轴就是它的对称轴
对称轴与抛物线的交点叫做抛物线的顶点
抛物线
顶点坐标
对称轴
位置
开口方向
极值
齐声朗读
y=x2
y=-x2
(0,0)
(0,0)
y轴:直线x=0
y轴:直线x=0
在x轴的上方(除顶点外)
在x轴的下方(除顶点外)
向上
向下
当x=0时,最小值为0。
当x=0时,最大值为0。
y=x2
y=-x2
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=2x2
8
…
2
0.5
0
0.5
2
4.5
8
…
4.5
y=-2x2
-8
…
-2
-0.5
0
-0.5
-2
-4.5
-8
…
-4.5
x
y
o
y=2x2
y=
.
3. a的绝对值越大,开口越小.
新知讲解
y=-2x2
1. y=2x2与y=-2x2图像关于x轴对称
y=x2
2.a的绝对值相等,开口大小相同.
y=ax2 a>0 a<0
图象
位置、开
口方向
对称性
顶点、最值
增减性
y
O
x
开口向上,在x轴上方.
y
O
x
开口向下,在x轴下方.
a的绝对值越大,开口越小.
关于y轴对称,对称轴是直线x=0.
顶点坐标是(0,0).
当x=0时,y最小值=0.
当x=0时,y最大值=0.
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
已知二次函数y=ax2(a≠0)的图像经过点(-2,-3).
(1)求a的值,并写出这个二次函数的解析式.
(2)说出这个二次函数的顶点坐标、对称轴、开口方向和图像的位置.
解:(1)把点(-2,-3)的坐标代入,得-3=,解得:a=-
这个二次函数的表达式是
(2)顶点为(0,0),对称轴为y轴,即直线x=0
因为a=-,所以这个二次函数图象的开口向下,顶点是图象上的最高点,图象在x轴的下方(除顶点外)。
新知讲解
新知讲解
y
O
x
抛物线y=ax2具有以下特征:
(1)开口方向由a的符号确定:
(3)对称轴是y轴,即直线x=0
(4)顶点坐标是(0,0),
当a>0时,(0,0)是最低点;当a<0时,(0,0)是最高点.
当a>0时,抛物线的开口向上。
当a<0时,抛物线的开口向下。
1分钟背诵
y=2x2
y=- x2
y=x2
y=-x2
(2)开口大小由|a| 的决定:
|a|越大,抛物线的开口越小;
|a|的绝对值相等,开口大小相同.
夯实基础,稳扎稳打
B
2.若抛物线y=ax2 (a ≠ 0),过点(-1,3)。
(1)则a的值是
(2)对称轴是 ,开口 。
(3)顶点坐标是 ,顶点是抛物线上的 。
抛物线在x轴的 方(除顶点外)。
3
y轴,即直线x=0
向上
(0,0)
最低点
上
y
O
x
3.若抛物线y=ax2 (a ≠ 0),过点(-1,-1)。
(1)则a的值是
(2)对称轴是 ,开口 。
(3)顶点坐标是 ,顶点是抛物线上的 。
抛物线在x轴的 方(除顶点外)。
-1
y轴,即直线x=0
向下
(0,0)
最高点
下
y
O
x
连续递推,豁然开朗
4.已知抛物线y=ax2经过点A(-2,-8).
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上.
(3)求出此抛物线上纵坐标为-6的点的坐标.
解(1)把(-2,-8)代入y=ax2,得:-8=a(-2)2, 4a=-8, a= -2,
所求函数解析式为 y= -2x2.
(2)当x=-1时,y=-2×(-1)2=-2≠-4,
所以点B(-1,-4)不在此抛物线上,
(3)由-6=-2x2 ,得x2=3, x=
所以纵坐标为-6的点有两个,它们分别是 ( ,-6), (- ,-6)
.
水平线y=-6
y=-2x2
纵坐标相同: 对称点
5.已知函数y=ax2与y=
.
x
0
y
y=
P
抛物线的开口向下
a<0
(2)抛物线开口向下,即m+3<0,所以m<-3,即m=-4
(3)抛物线有最低点,开口向上,即m+3>0,所以m>-3,即m=1
顶点坐标为(0,0),对称轴是y轴。
6、已知函数的图象是抛物线
(1)求m的值;
(2)当m为何值时,抛物线的开口向下?
(3)当m为何值时,抛物线有最低点?并写出它的顶点坐标和对称轴。
.
解:(1)因为函数是抛物线,所以此函数是二次函数
即:且m+3≠0
解得:m=-4,m=1
.
思维拓展,更上一层
7.如图,四边形OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,求a的值.
D
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
