浙教版八年级下册 2.2.2一元二次方程的解法 课件(15张PPT)
文档属性
| 名称 | 浙教版八年级下册 2.2.2一元二次方程的解法 课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 904.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-21 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
永康市空中希望课堂
八 年 级 数学 下 册
《2.2一元二次方程的解法》
(1)x2-4=0 (2)25x2=16
解:(x+2)(x-2)=0
∴x+2=0或x-2=0
∴x1=-2, x2=2
你还有其它的解法吗
用因式分解法解下列方程:
回顾旧知
解: 25x2-16=0
∴5x+4=0或5x-4=0
∴(5x+4)(5x-4)=0
∴x1= , x2=
(3)(x-3)2=25
解: (x-3)2-25=0
∴x+2=0,或x-8=0
∴x1=-2, x2=8
[(x-3)+5][(x-3)-5]=0
一元二次方程 一元一次方程
因式分解
x2+6x=1
你能用因式分解法解吗
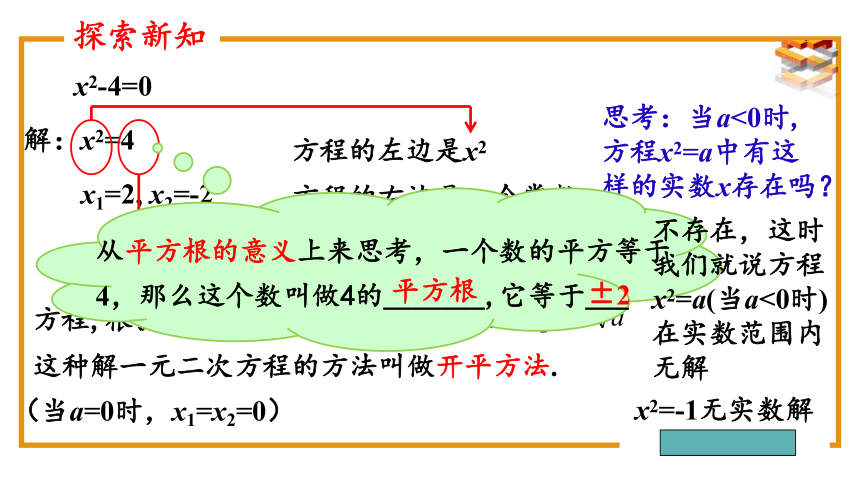
x2-4=0
探索新知
解:x2=4
x1=2, x2=-2
方程的左边是x2
方程的右边是一个常数
一般地,对于形如x2=a 的
方程,根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.
(a是常数且a≥0)
思考:当a<0时,方程x2=a中有这样的实数x存在吗?
从平方根的意义上来思考,一个数的平方等于4,那么这个数叫做4的_______,它等于___
平方根
±2
不存在,这时我们就说方程x2=a(当a<0时)在实数范围内无解
x2=-1无实数解
(当a=0时,x1=x2=0)
小试牛刀
填空
(1)方程 x2 =49的根是 ;
(2) 方程 x2 =0.25的根是 ;
(3)方程 2x2 =14的根是 ;
x1=7, x2=﹣7
x1=0.5, x2=﹣0.5
例题讲解
(2)25x2=16
(3)(x-3)2=25
解:
解:
思考:
这个方程符合x2=a的形式吗?或者可以转化为x2=a的形式吗?
∴x1= , x2=
(5x)2=16
x2 =a
5x=4或5x=-4
∴x1= , x2=
思考:
这个方程能用上述的方法求解吗?
x2 =a
x-3=5,或x-3=-5
∴x1=8, x2=-2
(4)(2x-5)2=7
解:
总结归纳
开平方法解一元二次方程的基本步骤:
(1)将方程变形成x2 =a (a为常数且a ≥ 0)的形式
(2)用开平方法将方程化为一元一次方程
这里的x可以是表示单独的未知数,也可以是含未知数的代数式
(1)x2-4=0
解:x2=4
x1=2, x2=-2
(2)25x2=16
解:
∴x1= , x2=
(3)(x-3)2=25
解:
x-3=5,或x-3=-5
∴x1=8, x2=-2
(4)(2x-5)2=7
解:
5x=4或5x=-4
思考:
什么样的方程可以用开平方法解方程?
形如x2=a(a ≥ 0)的形式的方程
方程x2=a(a ≥ 0)里的x在上述方程中分别指的是什么?
x
x-3
2x-5
x或5x
(3)解一元一次方程(注意化简)
(4)写出原方程的解
小试牛刀
用开平方法解下列方程:
解:
解:
解:
解:
解方程:
合作探究
x2-6x=16
思考:
方程能变形成x2 =a的形式吗
把一元二次方程的左边配成一个完全平方式,右边为一个非负常数,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
x2-6x+9=16+9
(x-3)2=25
∴x1=-2, x2=8
(依据是什么?)
等式的基本性质
x2 =a(a是常数且a ≥ 0)
x2+2x+___=(_____)2 x2-2x+___=(_____)2
x2+4x+___=(_____)2 x2-4x+___=(_____)2
x2+6x+___=(_____)2 x2-6x+___=(_____)2
x2+10x+___=(_____)2 x2-10x+___=(_____)2
12
x+1
12
x-1
22
x+2
22
x-2
32
x+3
32
x-3
52
x+5
52
x-5
添上一个适当的数,使下列的多项式成为一个完全平方式
规律探索
思考:
方程的二次项系数有什么特点?
方程的二次项系数等于1
方程的左边,一次项系数和常数项之间有什么关系?
常数项等于一次项系数一半的的平方
x2+3x+___=(________)2
x2+px+___=(________)2
(-1)2
(-2)2
(-3)2
(-5)2
例5 用配方法解下列一元二次方程:
解(1)
则
解得
方程两边同时加上9,得
即
例题讲解
方程的一次项系数是多少?
方程两边同时加上多少?
问题1:
问题2:
例5 用配方法解下列一元二次方程:
解(2)
则
解得
即
移项,得
方程两边同时加上(-),得
5
2
2
例题讲解
方程的一次项系数是多少?
方程两边同时加上多少?
问题1:
问题2:
思考:用配方法解二次项系数为1的一元二次方程的步骤是什么?
移项
配方
开方
定解
总结归纳
配方法解二次项系数为1的一元二次方程的基本步骤:
1.移项:把常数项移到方程的右边
2.配方:方程两边都加上一次项系数一半的平方,
转化为x2 =a(a为常数且a ≥ 0)的形式
3.开方:用开平方法将方程化为一元一次方程
5.定解:写出原方程的解
4.求解:求两个一元一次方程的解
小试牛刀
用配方法解下列方程:
(3)-x2+4x-3= 0
(2)x2+12x=-9
(1)x2-2x-4=0
解:
x2-2x=4
x2-2x+1=4+1
(x-1)2=5
解:
x2+12x+62=-9+62
x2+12x+62=27
(x+6)2=27
解:
x2-4x+3= 0
x2-4x=-3
x2-4x+4=-3+4
(x-2)2=1
x-2=1或x-2=-1
x1=3,x2=1
课堂小结
一元二次方程的解法
因式分解法:方程 A×B=0
配方法:
公式法
二次项系数为1的一元二次方程:
二次项系数不为1的一元二次方程
我们继续要探究的问题…
①移项
②配方
③开方
④求解(两个一元一次方程的解)
⑤定解
二次 一次
因式分解
开平方
开平方法:方程 x2 =a
(a是常数且a ≥ 0)
自我检测
(1)x2-6x=-8 (2)x2-2x-199=0 (3)x2+3x+2=0 (4)-x2+5x+6=0
2.用配方法解下列方程:
(1)x2-81=0 (2)2x2=50 (3)(x+1)2=4
1.选择适当的方法解下列方程:
3. 解方程:
(1) (x+1)2+4(x+1)=-3 (2)- x2+4x-3=0
4.工人师傅为了修屋顶,把一梯子搁在墙上,梯子与屋檐的接触处到底端的长AB=5米,墙高AC=4米,问梯子底端点离墙的距离BC是多少
永康市空中希望课堂
八 年 级 数学 下 册
《2.2一元二次方程的解法》
(1)x2-4=0 (2)25x2=16
解:(x+2)(x-2)=0
∴x+2=0或x-2=0
∴x1=-2, x2=2
你还有其它的解法吗
用因式分解法解下列方程:
回顾旧知
解: 25x2-16=0
∴5x+4=0或5x-4=0
∴(5x+4)(5x-4)=0
∴x1= , x2=
(3)(x-3)2=25
解: (x-3)2-25=0
∴x+2=0,或x-8=0
∴x1=-2, x2=8
[(x-3)+5][(x-3)-5]=0
一元二次方程 一元一次方程
因式分解
x2+6x=1
你能用因式分解法解吗
x2-4=0
探索新知
解:x2=4
x1=2, x2=-2
方程的左边是x2
方程的右边是一个常数
一般地,对于形如x2=a 的
方程,根据平方根的定义,可解得
这种解一元二次方程的方法叫做开平方法.
(a是常数且a≥0)
思考:当a<0时,方程x2=a中有这样的实数x存在吗?
从平方根的意义上来思考,一个数的平方等于4,那么这个数叫做4的_______,它等于___
平方根
±2
不存在,这时我们就说方程x2=a(当a<0时)在实数范围内无解
x2=-1无实数解
(当a=0时,x1=x2=0)
小试牛刀
填空
(1)方程 x2 =49的根是 ;
(2) 方程 x2 =0.25的根是 ;
(3)方程 2x2 =14的根是 ;
x1=7, x2=﹣7
x1=0.5, x2=﹣0.5
例题讲解
(2)25x2=16
(3)(x-3)2=25
解:
解:
思考:
这个方程符合x2=a的形式吗?或者可以转化为x2=a的形式吗?
∴x1= , x2=
(5x)2=16
x2 =a
5x=4或5x=-4
∴x1= , x2=
思考:
这个方程能用上述的方法求解吗?
x2 =a
x-3=5,或x-3=-5
∴x1=8, x2=-2
(4)(2x-5)2=7
解:
总结归纳
开平方法解一元二次方程的基本步骤:
(1)将方程变形成x2 =a (a为常数且a ≥ 0)的形式
(2)用开平方法将方程化为一元一次方程
这里的x可以是表示单独的未知数,也可以是含未知数的代数式
(1)x2-4=0
解:x2=4
x1=2, x2=-2
(2)25x2=16
解:
∴x1= , x2=
(3)(x-3)2=25
解:
x-3=5,或x-3=-5
∴x1=8, x2=-2
(4)(2x-5)2=7
解:
5x=4或5x=-4
思考:
什么样的方程可以用开平方法解方程?
形如x2=a(a ≥ 0)的形式的方程
方程x2=a(a ≥ 0)里的x在上述方程中分别指的是什么?
x
x-3
2x-5
x或5x
(3)解一元一次方程(注意化简)
(4)写出原方程的解
小试牛刀
用开平方法解下列方程:
解:
解:
解:
解:
解方程:
合作探究
x2-6x=16
思考:
方程能变形成x2 =a的形式吗
把一元二次方程的左边配成一个完全平方式,右边为一个非负常数,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
x2-6x+9=16+9
(x-3)2=25
∴x1=-2, x2=8
(依据是什么?)
等式的基本性质
x2 =a(a是常数且a ≥ 0)
x2+2x+___=(_____)2 x2-2x+___=(_____)2
x2+4x+___=(_____)2 x2-4x+___=(_____)2
x2+6x+___=(_____)2 x2-6x+___=(_____)2
x2+10x+___=(_____)2 x2-10x+___=(_____)2
12
x+1
12
x-1
22
x+2
22
x-2
32
x+3
32
x-3
52
x+5
52
x-5
添上一个适当的数,使下列的多项式成为一个完全平方式
规律探索
思考:
方程的二次项系数有什么特点?
方程的二次项系数等于1
方程的左边,一次项系数和常数项之间有什么关系?
常数项等于一次项系数一半的的平方
x2+3x+___=(________)2
x2+px+___=(________)2
(-1)2
(-2)2
(-3)2
(-5)2
例5 用配方法解下列一元二次方程:
解(1)
则
解得
方程两边同时加上9,得
即
例题讲解
方程的一次项系数是多少?
方程两边同时加上多少?
问题1:
问题2:
例5 用配方法解下列一元二次方程:
解(2)
则
解得
即
移项,得
方程两边同时加上(-),得
5
2
2
例题讲解
方程的一次项系数是多少?
方程两边同时加上多少?
问题1:
问题2:
思考:用配方法解二次项系数为1的一元二次方程的步骤是什么?
移项
配方
开方
定解
总结归纳
配方法解二次项系数为1的一元二次方程的基本步骤:
1.移项:把常数项移到方程的右边
2.配方:方程两边都加上一次项系数一半的平方,
转化为x2 =a(a为常数且a ≥ 0)的形式
3.开方:用开平方法将方程化为一元一次方程
5.定解:写出原方程的解
4.求解:求两个一元一次方程的解
小试牛刀
用配方法解下列方程:
(3)-x2+4x-3= 0
(2)x2+12x=-9
(1)x2-2x-4=0
解:
x2-2x=4
x2-2x+1=4+1
(x-1)2=5
解:
x2+12x+62=-9+62
x2+12x+62=27
(x+6)2=27
解:
x2-4x+3= 0
x2-4x=-3
x2-4x+4=-3+4
(x-2)2=1
x-2=1或x-2=-1
x1=3,x2=1
课堂小结
一元二次方程的解法
因式分解法:方程 A×B=0
配方法:
公式法
二次项系数为1的一元二次方程:
二次项系数不为1的一元二次方程
我们继续要探究的问题…
①移项
②配方
③开方
④求解(两个一元一次方程的解)
⑤定解
二次 一次
因式分解
开平方
开平方法:方程 x2 =a
(a是常数且a ≥ 0)
自我检测
(1)x2-6x=-8 (2)x2-2x-199=0 (3)x2+3x+2=0 (4)-x2+5x+6=0
2.用配方法解下列方程:
(1)x2-81=0 (2)2x2=50 (3)(x+1)2=4
1.选择适当的方法解下列方程:
3. 解方程:
(1) (x+1)2+4(x+1)=-3 (2)- x2+4x-3=0
4.工人师傅为了修屋顶,把一梯子搁在墙上,梯子与屋檐的接触处到底端的长AB=5米,墙高AC=4米,问梯子底端点离墙的距离BC是多少
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
