浙教版八年级下册 4.4 平行四边形的判定 课件(共18张PPT)
文档属性
| 名称 | 浙教版八年级下册 4.4 平行四边形的判定 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 214.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-21 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
平行四边形的判定
知识梳理
平行四边形的判定
边
角
对角线
对边平行且相等
对角相等;邻角互补
对角线互相平分
两组对边分别平行的四边形
一组对边平行且相等的四边形
两组对边分别相等的四边形
对角线互相平分的四边形
对称性
中心对称图形
平行四边形的性质
例题精讲
如图,在□ABCD中,若AD=3 cm,AB=5 cm,则□ABCD的周长为_______cm .
3
3
5
5
16
例1:
例题精讲
如图,在□ABCD中,若AD=3 cm,AB=5 cm,AE平分∠DAB,则CE的长为____cm .
变式1:
3
3
5
5
AB∥CD
∠1= ∠2
1
2
3
AE平分∠DAB
∠1= ∠3
∠2= ∠3
DE= AD=3
2
例题精讲
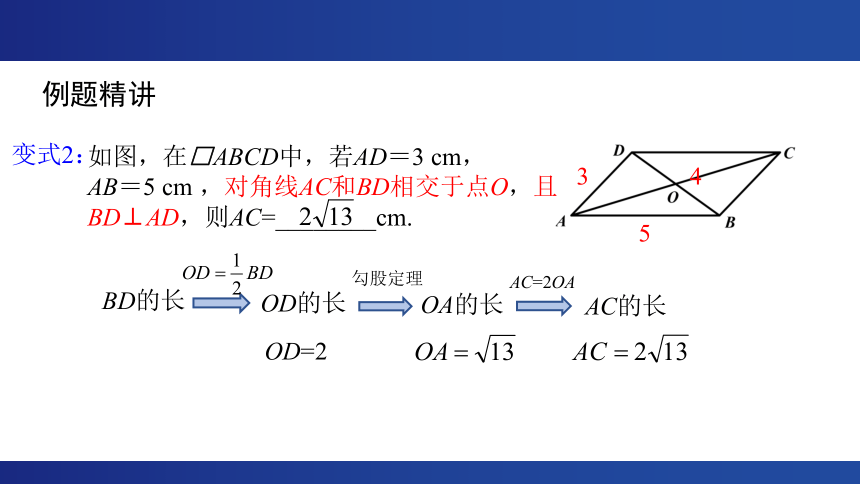
如图,在□ABCD中,若AD=3 cm,
AB=5 cm ,对角线AC和BD相交于点O,且BD⊥AD,则AC=________cm.
变式2:
3
5
4
AC的长
OA的长
OD的长
BD的长
勾股定理
AC=2OA
OD=2
例题精讲
如图,在□ABCD中,若∠B+∠D=260°,
则∠C=________ °.
变式3:
∠B=∠D=130°
方法1:
∠C=180°-130°=50°
50
方法2:
∠A+∠C=360°-260°= 100°
∠C=∠A=50°
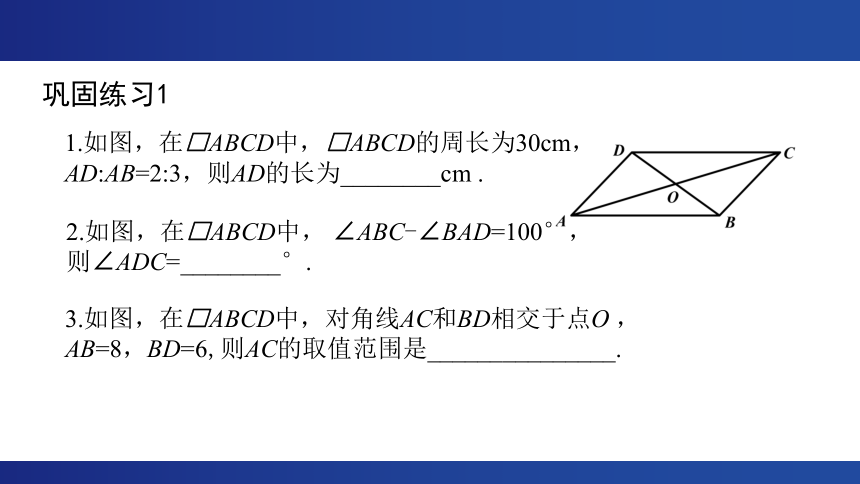
巩固练习1
1.如图,在□ABCD中,□ABCD的周长为30cm,
AD:AB=2:3,则AD的长为________cm .
2.如图,在□ABCD中, ∠ABC-∠BAD=100°,
则∠ADC=________°.
3.如图,在□ABCD中,对角线AC和BD相交于点O ,
AB=8,BD=6,则AC的取值范围是_______________.
巩固练习1
1.如图,在□ABCD中,□ABCD的周长为30cm,
AD:AB=2:3,则AD的长为________cm .
AD+AB=15
方法1:
方法2:
设AD=2x,AB=3x
AD+AB=5x=15
x=3
6
AD=2x=6
方程思想
巩固练习1
1.如图,在□ABCD中,□ABCD的周长为30cm,
AD:AB=2:3,则AD的长为________cm .
2.如图,在□ABCD中, ∠ABC-∠BAD=100°,
则∠ADC=________°.
6
x
y
∠ADC=∠ABC=140°
140
巩固练习1
1.如图,在□ABCD中,□ABCD的周长为30cm,
AD:AB=2:3,则AD的长为________cm .
2.如图,在□ABCD中, ∠ABC-∠BAD=100°,
则∠ADC=________°.
3.如图,在□ABCD中,对角线AC和BD相交于点O ,
AB=8,BD=6,则AC的取值范围是_______________.
6
140
6
8
3
3
OA的取值范围
AC=2OA
5<OA<11
10<AC<22
例题精讲
如图,在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF.
求证:四边形AECF是平行四边形.
AD∥BC,AD=BC
AB∥DC,AB=DC
∠ABC=∠ADC
∠DAB=∠DCB
OA=OC,OB=OD
方法1:
证明两组对边分别相等
1
2
∴∠1=∠2
又∵ DE=BF
∴ △ADE≌ △CBF
∴AE=CF
在□ ABCD中,
AD∥BC,AD=BC
证明:
同理可得CE=AF
∴四边形AECF是平行四边形
例2:
例题精讲
如图,在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF.
求证:四边形AECF是平行四边形.
方法2:
证明一组对边平行且相等
1
2
∴∠1=∠2
又∵ DE=BF
∴ △ADE≌ △CBF
∴AE=CF
在□ ABCD中,
AD∥BC,AD=BC
证明:
,∠DEA=∠BFC
∴四边形AECF是平行四边形
AE ∥ CF
∴180°-∠DEA= 180°- ∠BFC
∠3=∠4
3
4
∴
即
例2:
例题精讲
如图,在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF.
求证:四边形AECF是平行四边形.
AD∥BC,AD=BC
AB∥DC,AB=DC
∠ABC=∠ADC
∠DAB=∠DCB
OA=OC,OB=OD
方法3:
证明对角线互相平分
∵ DE=BF
OE=OF
在□ ABCD中,
∴四边形AECF是平行四边形
OD-DE= OB-BF
证明:
OA=OC,OB=OD
?
?
∴
即
例2:
如图,在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF,点G和点H在对角线AC上,且CG=AH.
请判断EG和HF的关系,并说明理由.
变式4:
例题精讲
方法1:
利用三角形全等
EG∥HF,EG=HF
△EOG≌ △FOH
EG=HF,∠EGO=∠FHO
EG∥HF
如图,在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF,点G和点H在对角线AC上,且CG=AH.
请判断EG和HF的关系,并说明理由.
变式4:
例题精讲
方法1:
利用三角形全等
EG∥HF,EG=HF
△EOG≌ △FOH
EG=HF,∠EGO=∠FHO
EG∥HF
方法2:
证明EG和HF所在的四边形是平行四边形
OE=OF
OH=OG
四边形EHFG是平行四边形
EG∥HF,EG=HF
转化思想
如图,在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF,过点O的直线分别交边DC,AB于点P,点Q.
证明:EQ=PF.
变式5:
巩固练习2
EQ=PF
□EQFP
OE=OF
OP=OQ
△DOP≌△BOQ
1
2
3
4
∠1=∠2
∠3=∠4
□ABCD
OB=OD
AB∥CD
在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF,过点O的直线分别交直线DC,AB于点P,点Q.
结论是否仍然成立?
变式6:
巩固练习2
始终存在□EQFP,结论仍然成立
分类讨论
课堂小结
1.知识要点
平行四边形的性质和判定(从边、角、对角线方面考虑)
平行四边形是中心对称图形
2.思想方法:
方程思想、
转化思想、
分类讨论思想
平行四边形的判定
知识梳理
平行四边形的判定
边
角
对角线
对边平行且相等
对角相等;邻角互补
对角线互相平分
两组对边分别平行的四边形
一组对边平行且相等的四边形
两组对边分别相等的四边形
对角线互相平分的四边形
对称性
中心对称图形
平行四边形的性质
例题精讲
如图,在□ABCD中,若AD=3 cm,AB=5 cm,则□ABCD的周长为_______cm .
3
3
5
5
16
例1:
例题精讲
如图,在□ABCD中,若AD=3 cm,AB=5 cm,AE平分∠DAB,则CE的长为____cm .
变式1:
3
3
5
5
AB∥CD
∠1= ∠2
1
2
3
AE平分∠DAB
∠1= ∠3
∠2= ∠3
DE= AD=3
2
例题精讲
如图,在□ABCD中,若AD=3 cm,
AB=5 cm ,对角线AC和BD相交于点O,且BD⊥AD,则AC=________cm.
变式2:
3
5
4
AC的长
OA的长
OD的长
BD的长
勾股定理
AC=2OA
OD=2
例题精讲
如图,在□ABCD中,若∠B+∠D=260°,
则∠C=________ °.
变式3:
∠B=∠D=130°
方法1:
∠C=180°-130°=50°
50
方法2:
∠A+∠C=360°-260°= 100°
∠C=∠A=50°
巩固练习1
1.如图,在□ABCD中,□ABCD的周长为30cm,
AD:AB=2:3,则AD的长为________cm .
2.如图,在□ABCD中, ∠ABC-∠BAD=100°,
则∠ADC=________°.
3.如图,在□ABCD中,对角线AC和BD相交于点O ,
AB=8,BD=6,则AC的取值范围是_______________.
巩固练习1
1.如图,在□ABCD中,□ABCD的周长为30cm,
AD:AB=2:3,则AD的长为________cm .
AD+AB=15
方法1:
方法2:
设AD=2x,AB=3x
AD+AB=5x=15
x=3
6
AD=2x=6
方程思想
巩固练习1
1.如图,在□ABCD中,□ABCD的周长为30cm,
AD:AB=2:3,则AD的长为________cm .
2.如图,在□ABCD中, ∠ABC-∠BAD=100°,
则∠ADC=________°.
6
x
y
∠ADC=∠ABC=140°
140
巩固练习1
1.如图,在□ABCD中,□ABCD的周长为30cm,
AD:AB=2:3,则AD的长为________cm .
2.如图,在□ABCD中, ∠ABC-∠BAD=100°,
则∠ADC=________°.
3.如图,在□ABCD中,对角线AC和BD相交于点O ,
AB=8,BD=6,则AC的取值范围是_______________.
6
140
6
8
3
3
OA的取值范围
AC=2OA
5<OA<11
10<AC<22
例题精讲
如图,在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF.
求证:四边形AECF是平行四边形.
AD∥BC,AD=BC
AB∥DC,AB=DC
∠ABC=∠ADC
∠DAB=∠DCB
OA=OC,OB=OD
方法1:
证明两组对边分别相等
1
2
∴∠1=∠2
又∵ DE=BF
∴ △ADE≌ △CBF
∴AE=CF
在□ ABCD中,
AD∥BC,AD=BC
证明:
同理可得CE=AF
∴四边形AECF是平行四边形
例2:
例题精讲
如图,在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF.
求证:四边形AECF是平行四边形.
方法2:
证明一组对边平行且相等
1
2
∴∠1=∠2
又∵ DE=BF
∴ △ADE≌ △CBF
∴AE=CF
在□ ABCD中,
AD∥BC,AD=BC
证明:
,∠DEA=∠BFC
∴四边形AECF是平行四边形
AE ∥ CF
∴180°-∠DEA= 180°- ∠BFC
∠3=∠4
3
4
∴
即
例2:
例题精讲
如图,在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF.
求证:四边形AECF是平行四边形.
AD∥BC,AD=BC
AB∥DC,AB=DC
∠ABC=∠ADC
∠DAB=∠DCB
OA=OC,OB=OD
方法3:
证明对角线互相平分
∵ DE=BF
OE=OF
在□ ABCD中,
∴四边形AECF是平行四边形
OD-DE= OB-BF
证明:
OA=OC,OB=OD
?
?
∴
即
例2:
如图,在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF,点G和点H在对角线AC上,且CG=AH.
请判断EG和HF的关系,并说明理由.
变式4:
例题精讲
方法1:
利用三角形全等
EG∥HF,EG=HF
△EOG≌ △FOH
EG=HF,∠EGO=∠FHO
EG∥HF
如图,在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF,点G和点H在对角线AC上,且CG=AH.
请判断EG和HF的关系,并说明理由.
变式4:
例题精讲
方法1:
利用三角形全等
EG∥HF,EG=HF
△EOG≌ △FOH
EG=HF,∠EGO=∠FHO
EG∥HF
方法2:
证明EG和HF所在的四边形是平行四边形
OE=OF
OH=OG
四边形EHFG是平行四边形
EG∥HF,EG=HF
转化思想
如图,在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF,过点O的直线分别交边DC,AB于点P,点Q.
证明:EQ=PF.
变式5:
巩固练习2
EQ=PF
□EQFP
OE=OF
OP=OQ
△DOP≌△BOQ
1
2
3
4
∠1=∠2
∠3=∠4
□ABCD
OB=OD
AB∥CD
在□ABCD中,对角线AC和BD相交于点O ,点E和点F在对角线BD上,且DE=BF,过点O的直线分别交直线DC,AB于点P,点Q.
结论是否仍然成立?
变式6:
巩固练习2
始终存在□EQFP,结论仍然成立
分类讨论
课堂小结
1.知识要点
平行四边形的性质和判定(从边、角、对角线方面考虑)
平行四边形是中心对称图形
2.思想方法:
方程思想、
转化思想、
分类讨论思想
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
