浙教版八年级下册 5.1.2 矩形的判定 课件(共17张PPT)
文档属性
| 名称 | 浙教版八年级下册 5.1.2 矩形的判定 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 718.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-21 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
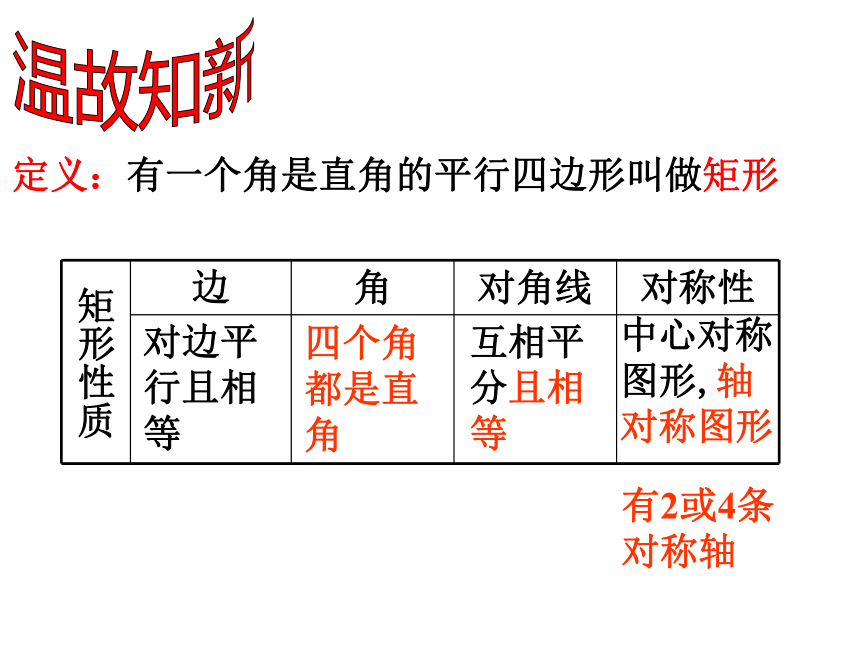
定义:有一个角是直角的平行四边形叫做矩形
矩形性质 边 角 对角线 对称性
四个角都是直角
对边平行且相等
互相平分且相等
中心对称图形,轴对称图形
有2或4条对称轴
有一个角是直角的平行四边形是矩形。
合作学习:
命题“矩形的四个角都是直角”的逆命题是什么?是真命题还是假命题?
逆命题:四个角都是直角的四边形是矩形。
真命题
判定1 (定义法)
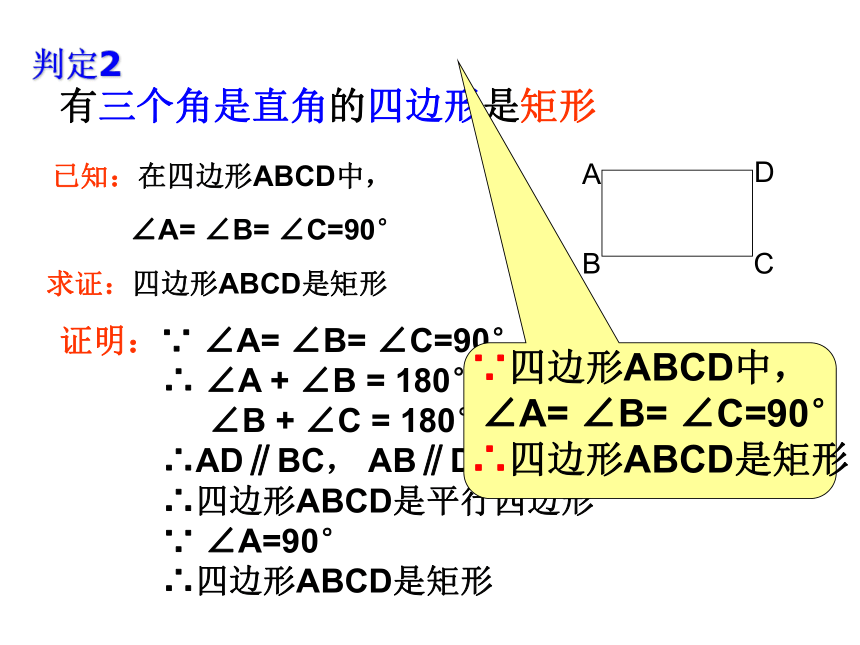
有三个角是直角的四边形是矩形
A
B
C
D
已知:在四边形ABCD中,
∠A= ∠B= ∠C=90°
求证:四边形ABCD是矩形
证明:∵ ∠A= ∠B= ∠C=90°
∴ ∠A + ∠B = 180°
∠B + ∠C = 180°
∴AD∥BC, AB∥DC
∴四边形ABCD是平行四边形
∵ ∠A=90°
∴四边形ABCD是矩形
∵四边形ABCD中,
∠A= ∠B= ∠C=90°
∴四边形ABCD是矩形
判定2
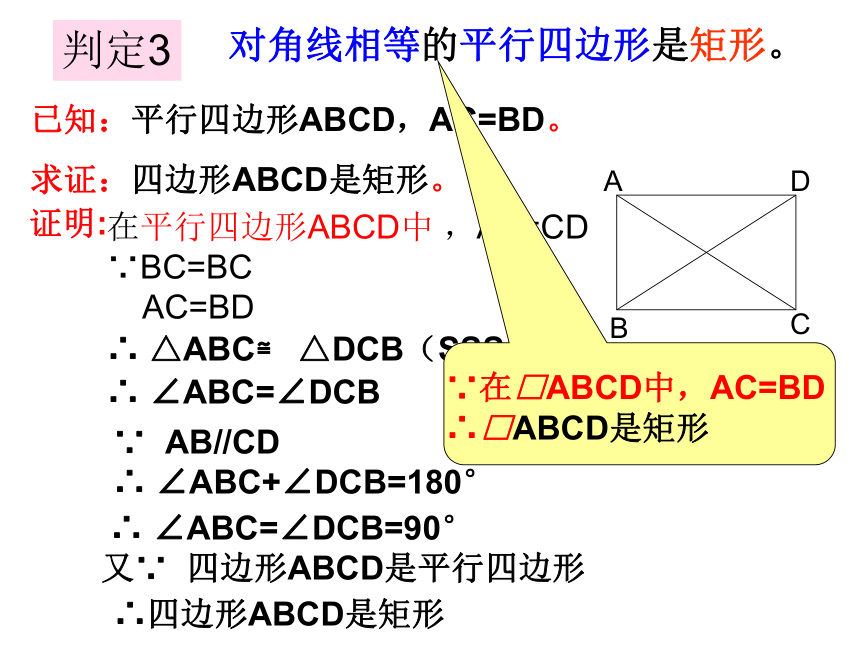
对角线相等的平行四边形是矩形。
已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
证明:
在平行四边形ABCD中 ,AB=CD
∵BC=BC
AC=BD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴四边形ABCD是矩形
∴ ∠ABC=∠DCB
判定3
∵在□ABCD中,AC=BD
∴□ABCD是矩形
(1)有一个角是直角的平行四边形是矩形。
(2)有三个角是直角的四边形是矩形。
(3)对角线相等的平行四边形是矩形。
矩形的判定方法:
四边形
平行四边形
平行四边形
做一做:判断下命题是否正确,并说明理由。
(1)对角互补的平行四边形是矩形。
(2)一组邻角相等的平行四边形是矩形。
(4)对角线相等的四边形是矩形。
(3)内角都相等的四边形是矩形。
正确
正确
不正确
正确
(5)对角线相等且平分的四边形是矩形。
正确
学以致用:
工作师傅做铝合金窗框分下面三个步骤进行:
(1)先截同两对符合规格的铝合金窗料,使
AB=CD,EF=GH
B
A
C
D
E
F
G
H
学以致用:
工作师傅做铝合金窗框分下面三个步骤进行:
(2)摆放成如图所示的四边形,则这时窗框的形状是____________形,数学原理是_______________________________________
B
A
C
D
E
F
G
H
平行四边
两组对边分别相等的四边形是平行四边形
学以致用:
工作师傅做铝合金窗框分下面三个步骤进行:
(3)将直角尺靠紧窗框的一个角(如图所示),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时,说明窗框合格,这时窗框是_____形,数学原理是_________________________________
B
A
C
D
E
F
G
H
矩
有一个角为直角的平行四边形是矩形
已知:如图,AC与BD相交于点O,AB CD 且∠1=∠2 。 求证:四边形ABCD是矩形
例 2 一张四边形纸板ABCD形状如图,
(1)若要从这张纸板中剪出一个平行四边形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可怎样剪?
E
F
G
H
⑵四边形ABCD满足什么情况下中点四边形EFGH为矩形?并说明理由.
解:分别取AB,BC,CD,DA的中点E,F,G,H,可剪得中点四边形EFGH为平行四边形.
两条对角线互相垂直,AC⊥BD
练1、已知:如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,求证四边形EFGH是矩形.
练2 如果平行四边形四个内角的平分线能够围成一个四边形,那么这个四边形是矩形.
已知:如图, ABCD的四个内角的
平分线分别相交于E、F、G、H,
求证:四边形 EFGH为矩形.
∴∠BGC=90°
同理可证∠AFB=∠AED=90°
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
证明:∵AB∥CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD
∴∠GBC=1/2∠ABC ∠GCB=1/2∠DCB
说能出你这节课的收获和体验让大家与你分享吗?
∠A= ∠B= ∠C=90°
ABCD
AC = BD
ABCD
∠A=90°
ABCD
是矩形
四边形ABCD
是矩形
课堂小结
知识链:
四边形
平行四边形
矩形
有一个角是直角
对角线相等
有三个角是直角
任意一个四边形,
三角直角定矩形。
对于平行四边形,
一个直角即可定;
对线相等也矩形。
矩形的判定口诀:
定义:有一个角是直角的平行四边形叫做矩形
矩形性质 边 角 对角线 对称性
四个角都是直角
对边平行且相等
互相平分且相等
中心对称图形,轴对称图形
有2或4条对称轴
有一个角是直角的平行四边形是矩形。
合作学习:
命题“矩形的四个角都是直角”的逆命题是什么?是真命题还是假命题?
逆命题:四个角都是直角的四边形是矩形。
真命题
判定1 (定义法)
有三个角是直角的四边形是矩形
A
B
C
D
已知:在四边形ABCD中,
∠A= ∠B= ∠C=90°
求证:四边形ABCD是矩形
证明:∵ ∠A= ∠B= ∠C=90°
∴ ∠A + ∠B = 180°
∠B + ∠C = 180°
∴AD∥BC, AB∥DC
∴四边形ABCD是平行四边形
∵ ∠A=90°
∴四边形ABCD是矩形
∵四边形ABCD中,
∠A= ∠B= ∠C=90°
∴四边形ABCD是矩形
判定2
对角线相等的平行四边形是矩形。
已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
证明:
在平行四边形ABCD中 ,AB=CD
∵BC=BC
AC=BD
∴ △ABC≌ △DCB(SSS)
∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴四边形ABCD是矩形
∴ ∠ABC=∠DCB
判定3
∵在□ABCD中,AC=BD
∴□ABCD是矩形
(1)有一个角是直角的平行四边形是矩形。
(2)有三个角是直角的四边形是矩形。
(3)对角线相等的平行四边形是矩形。
矩形的判定方法:
四边形
平行四边形
平行四边形
做一做:判断下命题是否正确,并说明理由。
(1)对角互补的平行四边形是矩形。
(2)一组邻角相等的平行四边形是矩形。
(4)对角线相等的四边形是矩形。
(3)内角都相等的四边形是矩形。
正确
正确
不正确
正确
(5)对角线相等且平分的四边形是矩形。
正确
学以致用:
工作师傅做铝合金窗框分下面三个步骤进行:
(1)先截同两对符合规格的铝合金窗料,使
AB=CD,EF=GH
B
A
C
D
E
F
G
H
学以致用:
工作师傅做铝合金窗框分下面三个步骤进行:
(2)摆放成如图所示的四边形,则这时窗框的形状是____________形,数学原理是_______________________________________
B
A
C
D
E
F
G
H
平行四边
两组对边分别相等的四边形是平行四边形
学以致用:
工作师傅做铝合金窗框分下面三个步骤进行:
(3)将直角尺靠紧窗框的一个角(如图所示),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时,说明窗框合格,这时窗框是_____形,数学原理是_________________________________
B
A
C
D
E
F
G
H
矩
有一个角为直角的平行四边形是矩形
已知:如图,AC与BD相交于点O,AB CD 且∠1=∠2 。 求证:四边形ABCD是矩形
例 2 一张四边形纸板ABCD形状如图,
(1)若要从这张纸板中剪出一个平行四边形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可怎样剪?
E
F
G
H
⑵四边形ABCD满足什么情况下中点四边形EFGH为矩形?并说明理由.
解:分别取AB,BC,CD,DA的中点E,F,G,H,可剪得中点四边形EFGH为平行四边形.
两条对角线互相垂直,AC⊥BD
练1、已知:如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,求证四边形EFGH是矩形.
练2 如果平行四边形四个内角的平分线能够围成一个四边形,那么这个四边形是矩形.
已知:如图, ABCD的四个内角的
平分线分别相交于E、F、G、H,
求证:四边形 EFGH为矩形.
∴∠BGC=90°
同理可证∠AFB=∠AED=90°
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
证明:∵AB∥CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD
∴∠GBC=1/2∠ABC ∠GCB=1/2∠DCB
说能出你这节课的收获和体验让大家与你分享吗?
∠A= ∠B= ∠C=90°
ABCD
AC = BD
ABCD
∠A=90°
ABCD
是矩形
四边形ABCD
是矩形
课堂小结
知识链:
四边形
平行四边形
矩形
有一个角是直角
对角线相等
有三个角是直角
任意一个四边形,
三角直角定矩形。
对于平行四边形,
一个直角即可定;
对线相等也矩形。
矩形的判定口诀:
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
