浙教版八年级下册 5.3.2 正方形的性质 课件 25张PPT
文档属性
| 名称 | 浙教版八年级下册 5.3.2 正方形的性质 课件 25张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 552.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 14:50:14 | ||
图片预览








文档简介
(共25张PPT)
有一组邻边相等且有一个角是直角的平行四边形是正方形。
定义法
菱形法
矩形法
有一个角是直角的菱形是正方形。
有一组邻边相等的矩形是正方形。
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
一组对边平行且相等
两组对边分别相等
对角线互相平分
四边形
平行四边形
矩形
菱形
两组对角分别相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
一组邻边相等
平行四边形
矩形
菱形
正方形
有一个角是直角
一组邻边相等
有一个角是直角
5.3.2 正方形的性质
知识回顾
有一个角是直角
一组邻边相等
一组邻边相等
有一个角是直角
一组邻边相等且一个角是直角
边: 对边平行
四边相等
角 :四个角都是直角
对角线: 相等
互相垂直、平分
每条对角线平分一组对角。
A
O
B
C
D
正方形具有什么性质
谈一谈
有一组邻边相等且有一个角是直角的平行四边形叫做正方形.
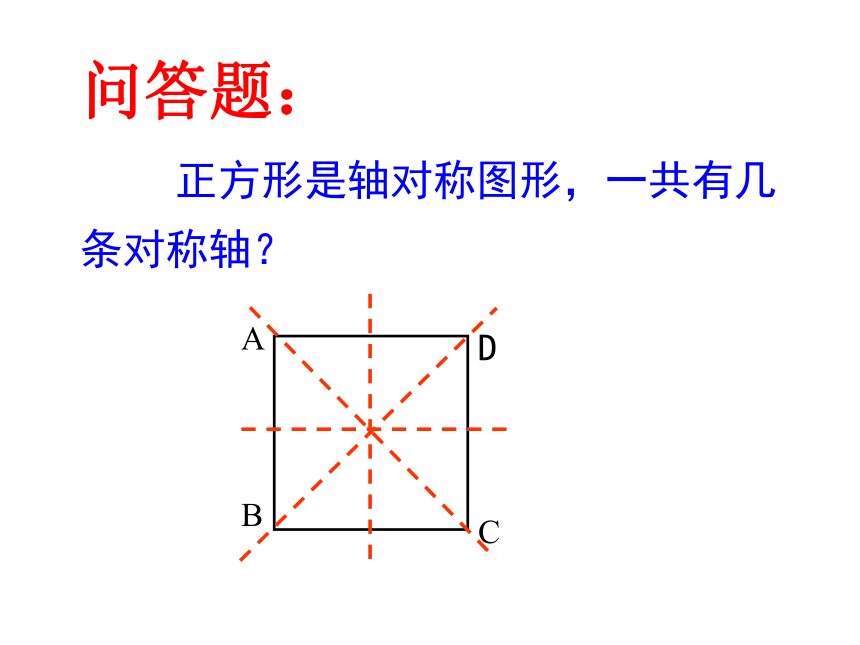
问答题:
A
B
C
D
正方形是轴对称图形,一共有几条对称轴?
正方形的四个角是直角,四条边都相等。
正方形的对角线相等,并且互相垂直平分,每条
对角线平分一组对角。
正方形是特殊的平行四边形,也是特殊的矩形,
也是特殊的菱形。
正方形的性质=
正方形具有而菱形不一定具有的性质是( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
选择
D
选择题
B
正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.
正方形的两条对角线把正方形
分成四个全等的等腰直角三角形。
O
A
B
C
D
判断题
√
( )
P127.课内练习2
2.如图,在正方形ABCD中,延长BC至E,使CE=AC,
求∠CAE的度数。
A
B
D
C
F
E
P.127课内练习3
如图,在正方形ABCD中,M是正方形内一点,且
MC=MD=AD,求∠BAM的度数?
P.127作业题3
如图,在正方形ABCD中,E、F分别是AD、CD
上的点,且DE=DF,BM⊥EF于点M,
求证:ME=MF
例2 已知:如图,在正方形ABCD中,G是对角线BD上的一点,GE⊥CD,GF⊥BC,E、F分别为垂足,连结AG,EF,试问AG与EF有怎样的关系?请说明理由.
P.127作业题4
如图,在正方形ABCD中,E、F分别是BC、CD
上的点,AE⊥BF
求证:AE=BF
P.127 作业题5
如图,在直角坐标系中,正方形的对角线交点是原
点O,两组对边分别与x轴,y轴平行,若正方形的
对角线长为 ,求正方形各顶点的坐标?
证明:
∵ GE⊥CD, GF⊥BC
∴ ∠GFC= ∠GEC =90°
(有三个角是直角的四边形是矩形)
又∵ ∠BCD =90°
∴ AG=CG
∴ 四边形FCEG是矩形
例2 已知:如图,在正方形ABCD中,G是对角线BD上的一点,GE⊥CD,GF⊥BC,E、F分别为垂足,连结AG,EF. 求证:AG=EF
如图,连结CG
在△AGD和△CGD中,
∠ADG=∠CDG(正方形的对角线平分一组对角)
DG=DG, AD=CD(正方形的四条边相等)
∴△AGD≌△CGD
∴ AG=EF
∴ EF=CG
(矩形的两条对角线相等)
例3、如图,正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
证明:
∴OA-OM=OB-ON
∴OM=ON
∴∠OMN=∠1=∠3=∠ONM=45°
又∵MN∥AB
∠1=∠2=∠3=45°
∴OA=OB AB=BC
∵四边形ABCD是正方形
即:AM=BN
∴△ABM≌△BCN
∴BM=CN
正方形的四个角是直角,四条边都相等。
正方形的对角线相等,并且互相垂直平分,每条
对角线平分一组对角。
正方形是特殊的平行四边形,也是特殊的矩形,
也是特殊的菱形。
正方形的性质=
1.掌握正方形的性质定理
2.会综合运用正方形的性质定理和判定定理来解决问题。
阅读课本P.126--至例2前为止,思考并准备回答下列问题:
1.小组从边、角、对角线、整体图形议一议有哪些性质?
2.正方形的一条对角线把正方形分成什么图形 因而,正方形问题 转化为什么问题来解决?
5分钟后比一比谁的自学效果好!
小组选一选:
1号
2号
3号
4号
P.127 课内练习2、3
P.127 作业题1、2、3、4、5
有一组邻边相等且有一个角是直角的平行四边形是正方形。
定义法
菱形法
矩形法
有一个角是直角的菱形是正方形。
有一组邻边相等的矩形是正方形。
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
一组对边平行且相等
两组对边分别相等
对角线互相平分
四边形
平行四边形
矩形
菱形
两组对角分别相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
一组邻边相等
平行四边形
矩形
菱形
正方形
有一个角是直角
一组邻边相等
有一个角是直角
5.3.2 正方形的性质
知识回顾
有一个角是直角
一组邻边相等
一组邻边相等
有一个角是直角
一组邻边相等且一个角是直角
边: 对边平行
四边相等
角 :四个角都是直角
对角线: 相等
互相垂直、平分
每条对角线平分一组对角。
A
O
B
C
D
正方形具有什么性质
谈一谈
有一组邻边相等且有一个角是直角的平行四边形叫做正方形.
问答题:
A
B
C
D
正方形是轴对称图形,一共有几条对称轴?
正方形的四个角是直角,四条边都相等。
正方形的对角线相等,并且互相垂直平分,每条
对角线平分一组对角。
正方形是特殊的平行四边形,也是特殊的矩形,
也是特殊的菱形。
正方形的性质=
正方形具有而菱形不一定具有的性质是( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
选择
D
选择题
B
正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直.
C、对角互补.
D、对角线相等.
正方形的两条对角线把正方形
分成四个全等的等腰直角三角形。
O
A
B
C
D
判断题
√
( )
P127.课内练习2
2.如图,在正方形ABCD中,延长BC至E,使CE=AC,
求∠CAE的度数。
A
B
D
C
F
E
P.127课内练习3
如图,在正方形ABCD中,M是正方形内一点,且
MC=MD=AD,求∠BAM的度数?
P.127作业题3
如图,在正方形ABCD中,E、F分别是AD、CD
上的点,且DE=DF,BM⊥EF于点M,
求证:ME=MF
例2 已知:如图,在正方形ABCD中,G是对角线BD上的一点,GE⊥CD,GF⊥BC,E、F分别为垂足,连结AG,EF,试问AG与EF有怎样的关系?请说明理由.
P.127作业题4
如图,在正方形ABCD中,E、F分别是BC、CD
上的点,AE⊥BF
求证:AE=BF
P.127 作业题5
如图,在直角坐标系中,正方形的对角线交点是原
点O,两组对边分别与x轴,y轴平行,若正方形的
对角线长为 ,求正方形各顶点的坐标?
证明:
∵ GE⊥CD, GF⊥BC
∴ ∠GFC= ∠GEC =90°
(有三个角是直角的四边形是矩形)
又∵ ∠BCD =90°
∴ AG=CG
∴ 四边形FCEG是矩形
例2 已知:如图,在正方形ABCD中,G是对角线BD上的一点,GE⊥CD,GF⊥BC,E、F分别为垂足,连结AG,EF. 求证:AG=EF
如图,连结CG
在△AGD和△CGD中,
∠ADG=∠CDG(正方形的对角线平分一组对角)
DG=DG, AD=CD(正方形的四条边相等)
∴△AGD≌△CGD
∴ AG=EF
∴ EF=CG
(矩形的两条对角线相等)
例3、如图,正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
证明:
∴OA-OM=OB-ON
∴OM=ON
∴∠OMN=∠1=∠3=∠ONM=45°
又∵MN∥AB
∠1=∠2=∠3=45°
∴OA=OB AB=BC
∵四边形ABCD是正方形
即:AM=BN
∴△ABM≌△BCN
∴BM=CN
正方形的四个角是直角,四条边都相等。
正方形的对角线相等,并且互相垂直平分,每条
对角线平分一组对角。
正方形是特殊的平行四边形,也是特殊的矩形,
也是特殊的菱形。
正方形的性质=
1.掌握正方形的性质定理
2.会综合运用正方形的性质定理和判定定理来解决问题。
阅读课本P.126--至例2前为止,思考并准备回答下列问题:
1.小组从边、角、对角线、整体图形议一议有哪些性质?
2.正方形的一条对角线把正方形分成什么图形 因而,正方形问题 转化为什么问题来解决?
5分钟后比一比谁的自学效果好!
小组选一选:
1号
2号
3号
4号
P.127 课内练习2、3
P.127 作业题1、2、3、4、5
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
