浙教版九年级上册 第3章 圆的基本性质 专题课件(共17张PPT)
文档属性
| 名称 | 浙教版九年级上册 第3章 圆的基本性质 专题课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 16:42:12 | ||
图片预览


文档简介
(共17张PPT)
圆
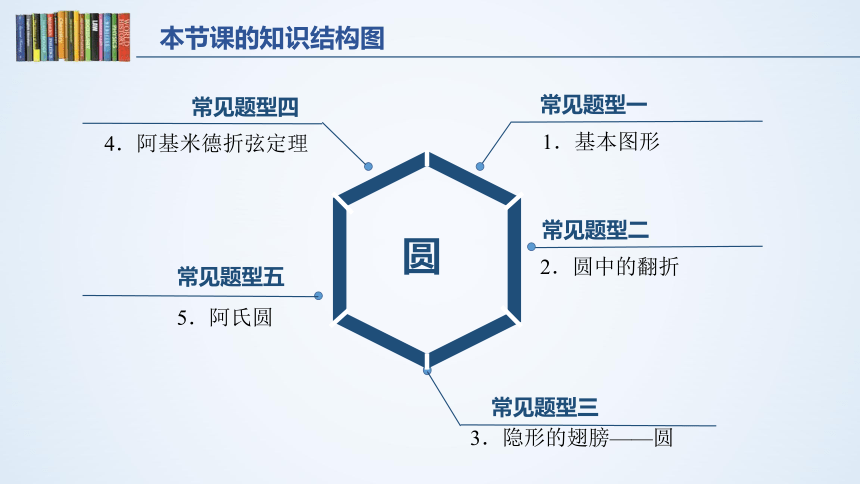
本节课的知识结构图
圆
常见题型一
1.基本图形
常见题型二
2.圆中的翻折
常见题型三
3.隐形的翅膀——圆
常见题型五
5.阿氏圆
常见题型四
4.阿基米德折弦定理
一.圆中常见图形
例1如图,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.
(1)试判断DE与BD是否相等,并说明理由;
(2)若BC=6,AB=5,求BE的长.
分析:(1)证明两条弦相等,通常转化为角或弧,连结AD,由于等腰三角形的性质“三线合一”即可得∠CAD=∠BAD.从而得证所求弦相等.
(2)求几何中的线段长度,初中阶段常用的两种方法为勾股定理和相似三角形的性质,如果两条路都走不通的话,可以考虑面积法等其他方法.显然此题三种方法皆可.
返回
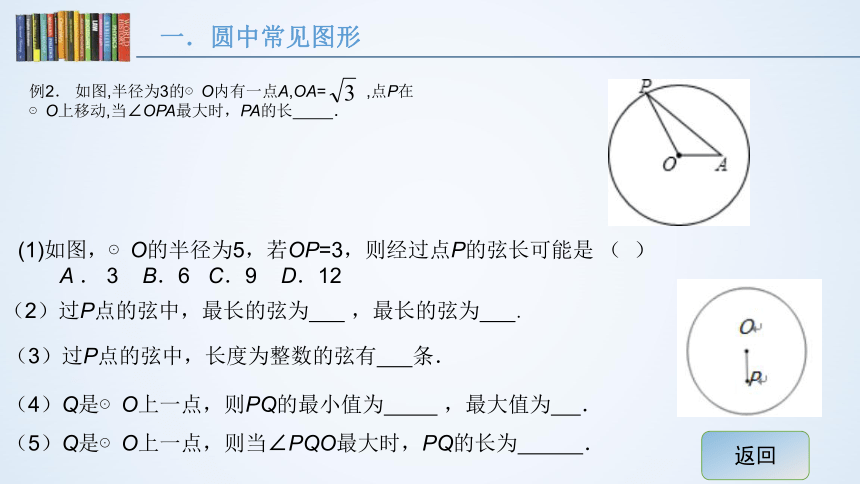
例2. 如图,半径为3的⊙O内有一点A,OA= ,点P在
⊙O上移动,当∠OPA最大时,PA的长 .
(1)如图,⊙O的半径为5,若OP=3,则经过点P的弦长可能是 ( )
A . 3 B.6 C.9 D.12
(2)过P点的弦中,最长的弦为 ,最长的弦为 .
(3)过P点的弦中,长度为整数的弦有 条.
(4)Q是⊙O上一点,则PQ的最小值为 ,最大值为 .
(5)Q是⊙O上一点,则当∠PQO最大时,PQ的长为 .
一.圆中常见图形
返回
返回
一.圆中常见图形
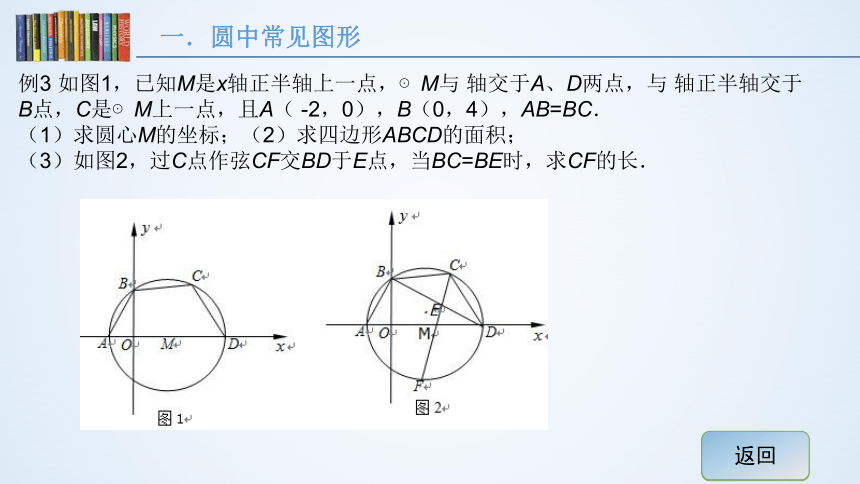
例3 如图1,已知M是x轴正半轴上一点,⊙M与 轴交于A、D两点,与 轴正半轴交于B点,C是⊙M上一点,且A( -2,0),B(0,4),AB=BC.
(1)求圆心M的坐标;(2)求四边形ABCD的面积;
(3)如图2,过C点作弦CF交BD于E点,当BC=BE时,求CF的长.
二、圆中的翻折
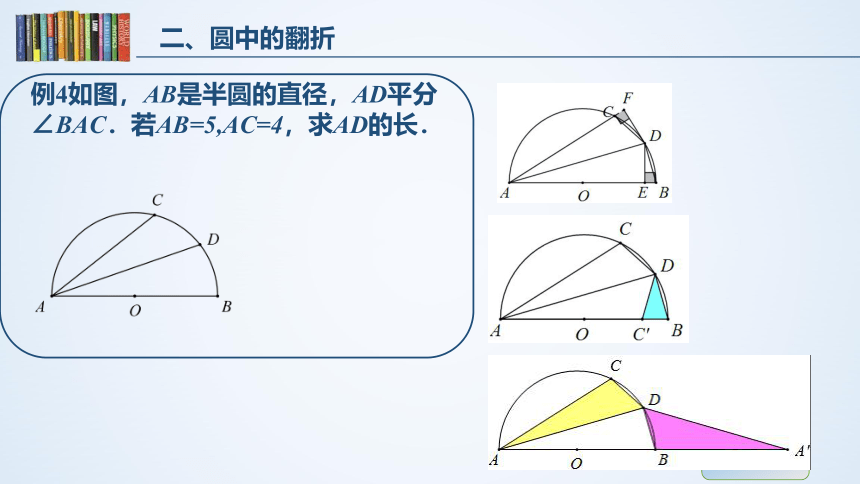
例4如图,AB是半圆的直径,AD平分∠BAC.若AB=5,AC=4,求AD的长.
返回
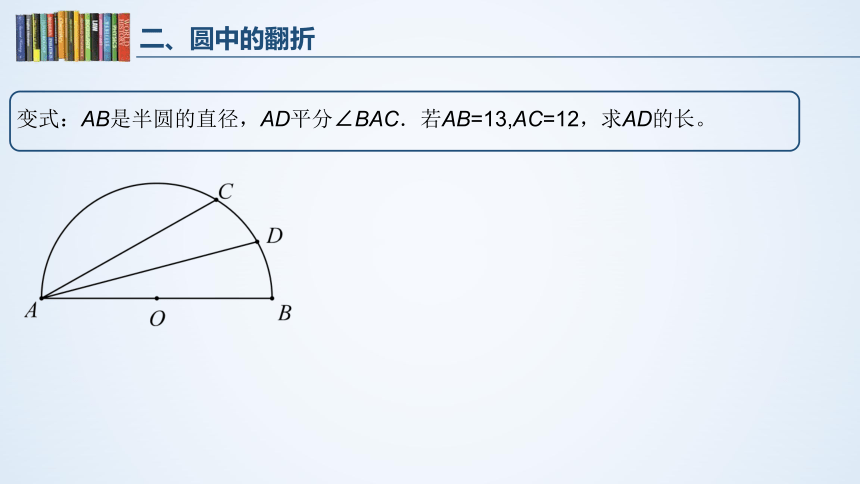
变式:AB是半圆的直径,AD平分∠BAC.若AB=13,AC=12,求AD的长。
二、圆中的翻折
例5如图,AB是半圆的直径,将弧AC沿AC翻折交直径于点D,若AD=4BD,求tanA.
二、圆中的翻折
变式:将弧AC沿AC翻折后恰好经过AB中点D.若圆的半径为 ,AB=8,则AC= .
二、圆中的翻折
三.隐形的翅膀——圆
返回
例6如图正方形ABCD的边长为2,M是AB的中点,E是BC上一点, 和B关
于ME轴对称.求 D的最小值.
分析:此类问题有时候难以得到突破口,同学们可以用实验法——画几个特殊位置的 ,然后观察 的位置有何规律,再进行猜想验证,从而寻到解题策略.
三.隐形的翅膀——圆
返回
变式1.已知如图△ABC中,∠BAC=60°,∠B=45°,AB=6,P是AC边上一点,过P作BC、AB的垂线.连结EF,垂足为E、F.则EF的最小值为 .
三.隐形的翅膀——圆
返回
变式2. 如图,A(1,0)、B(3,0),以AB为直径作⊙M,射线OF交⊙M于E、F两点,C为弧AB的中点,D为EF的中点.当射线绕O点旋转时,CD的最小值为 .
四、阿基米德折弦定理
例3如图,设AC=1,EA=2,D是BC的中点,
且DE⊥AB于点E.则EB= .
返回
四、阿基米德折弦定理
D是弧AB的中点,DE⊥AB CA+AE=EB
返回
四、阿基米德折弦定理
如图,已知等边△ABC内接于圆O,AB=√(2),D为弧AC上一点,∠ABD=45°,则△BDC的周长是 .
返回
E
五、阿氏圆
返回
例8已知正方形ABCD的边长为4,圆A的半径为2.E是圆A上一点.求 的最小值.
五、阿氏圆
返回
变式:如图,点A(0,4),B(-4,0),C(2,0),过A,B,C作外接圆,点D为圆上一动点,求 的最小值.
圆
本节课的知识结构图
圆
常见题型一
1.基本图形
常见题型二
2.圆中的翻折
常见题型三
3.隐形的翅膀——圆
常见题型五
5.阿氏圆
常见题型四
4.阿基米德折弦定理
一.圆中常见图形
例1如图,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.
(1)试判断DE与BD是否相等,并说明理由;
(2)若BC=6,AB=5,求BE的长.
分析:(1)证明两条弦相等,通常转化为角或弧,连结AD,由于等腰三角形的性质“三线合一”即可得∠CAD=∠BAD.从而得证所求弦相等.
(2)求几何中的线段长度,初中阶段常用的两种方法为勾股定理和相似三角形的性质,如果两条路都走不通的话,可以考虑面积法等其他方法.显然此题三种方法皆可.
返回
例2. 如图,半径为3的⊙O内有一点A,OA= ,点P在
⊙O上移动,当∠OPA最大时,PA的长 .
(1)如图,⊙O的半径为5,若OP=3,则经过点P的弦长可能是 ( )
A . 3 B.6 C.9 D.12
(2)过P点的弦中,最长的弦为 ,最长的弦为 .
(3)过P点的弦中,长度为整数的弦有 条.
(4)Q是⊙O上一点,则PQ的最小值为 ,最大值为 .
(5)Q是⊙O上一点,则当∠PQO最大时,PQ的长为 .
一.圆中常见图形
返回
返回
一.圆中常见图形
例3 如图1,已知M是x轴正半轴上一点,⊙M与 轴交于A、D两点,与 轴正半轴交于B点,C是⊙M上一点,且A( -2,0),B(0,4),AB=BC.
(1)求圆心M的坐标;(2)求四边形ABCD的面积;
(3)如图2,过C点作弦CF交BD于E点,当BC=BE时,求CF的长.
二、圆中的翻折
例4如图,AB是半圆的直径,AD平分∠BAC.若AB=5,AC=4,求AD的长.
返回
变式:AB是半圆的直径,AD平分∠BAC.若AB=13,AC=12,求AD的长。
二、圆中的翻折
例5如图,AB是半圆的直径,将弧AC沿AC翻折交直径于点D,若AD=4BD,求tanA.
二、圆中的翻折
变式:将弧AC沿AC翻折后恰好经过AB中点D.若圆的半径为 ,AB=8,则AC= .
二、圆中的翻折
三.隐形的翅膀——圆
返回
例6如图正方形ABCD的边长为2,M是AB的中点,E是BC上一点, 和B关
于ME轴对称.求 D的最小值.
分析:此类问题有时候难以得到突破口,同学们可以用实验法——画几个特殊位置的 ,然后观察 的位置有何规律,再进行猜想验证,从而寻到解题策略.
三.隐形的翅膀——圆
返回
变式1.已知如图△ABC中,∠BAC=60°,∠B=45°,AB=6,P是AC边上一点,过P作BC、AB的垂线.连结EF,垂足为E、F.则EF的最小值为 .
三.隐形的翅膀——圆
返回
变式2. 如图,A(1,0)、B(3,0),以AB为直径作⊙M,射线OF交⊙M于E、F两点,C为弧AB的中点,D为EF的中点.当射线绕O点旋转时,CD的最小值为 .
四、阿基米德折弦定理
例3如图,设AC=1,EA=2,D是BC的中点,
且DE⊥AB于点E.则EB= .
返回
四、阿基米德折弦定理
D是弧AB的中点,DE⊥AB CA+AE=EB
返回
四、阿基米德折弦定理
如图,已知等边△ABC内接于圆O,AB=√(2),D为弧AC上一点,∠ABD=45°,则△BDC的周长是 .
返回
E
五、阿氏圆
返回
例8已知正方形ABCD的边长为4,圆A的半径为2.E是圆A上一点.求 的最小值.
五、阿氏圆
返回
变式:如图,点A(0,4),B(-4,0),C(2,0),过A,B,C作外接圆,点D为圆上一动点,求 的最小值.
同课章节目录
