浙教版九年级上册 4.3 相似三角形 课件(共14张PPT)
文档属性
| 名称 | 浙教版九年级上册 4.3 相似三角形 课件(共14张PPT) |

|
|
| 格式 | PPT | ||
| 文件大小 | 583.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 16:52:56 | ||
图片预览


文档简介
(共14张PPT)
欣赏 观 察
4.3 相似三角形
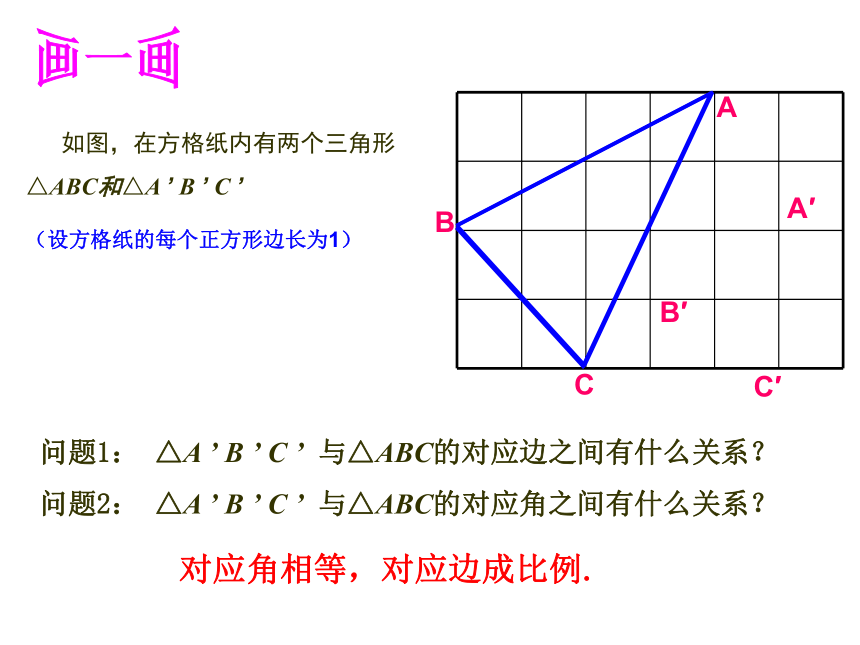
C
A
B
B′
A′
C′
如图,在方格纸内有两个三角形△ABC和△A ’ B ’ C ’
(设方格纸的每个正方形边长为1)
问题1: △A ’ B ’ C ’ 与△ABC的对应边之间有什么关系?
问题2: △A ’ B ’ C ’ 与△ABC的对应角之间有什么关系?
对应角相等,对应边成比例.
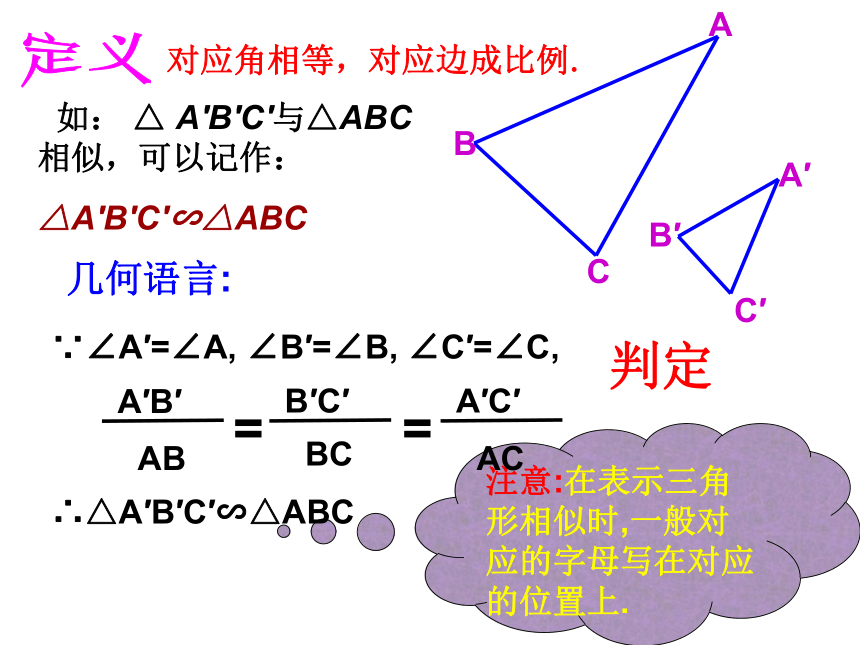
B′
A′
C′
C
A
B
如: △ A′B′C′与△ABC相似,可以记作:
△A′B′C′∽△ABC
注意:在表示三角形相似时,一般对应的字母写在对应的位置上.
几何语言:
∵∠A′=∠A, ∠B′=∠B, ∠C′=∠C,
AB
A′B′
BC
B′C′
AC
A′C′
=
=
∴△A′B′C′∽△ABC
对应角相等,对应边成比例.
判定
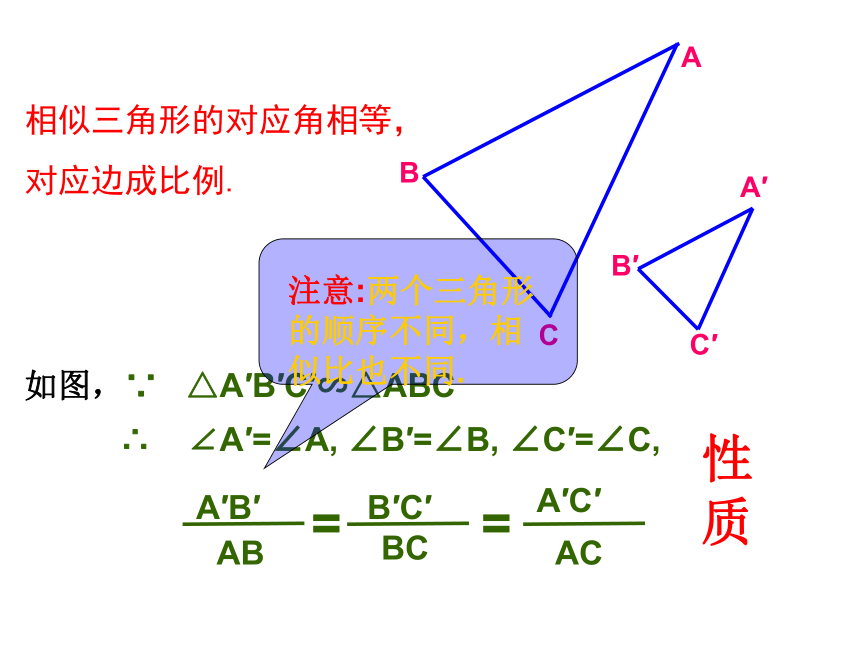
B
A
C
B′
A′
C′
相似三角形的对应角相等,对应边成比例.
如图,∵ △A′B′C′∽△ABC
∴ ∠A′=∠A, ∠B′=∠B, ∠C′=∠C,
AB
A′B′
BC
B′C′
AC
A′C′
=
=
注意:两个三角形的顺序不同,相似比也不同.
性质
(4)两个全等三角形一定相似。 ( )
(3)两个等边三角形一定相似。 ( )
(1)两个直角三角形一定相似。 ( )
(2)两个等腰三角形一定相似。 ( )
30
45
(5)两个等腰直角三角形一定相似. ( )
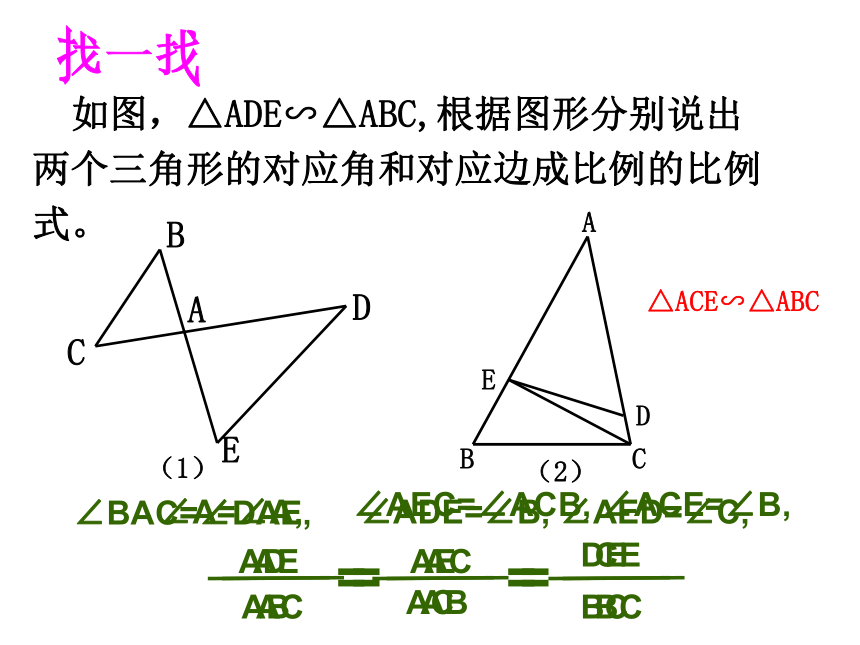
如图,△ADE∽△ABC,根据图形分别说出两个三角形的对应角和对应边成比例的比例式。
A
B
D
E
C
(1)
AB
AD
AC
AE
BC
DE
=
=
∠ADE=∠B, ∠AED=∠C,
∠A=∠A,
∠BAC=∠DAE,
A
B
C
E
D
(2)
△ACE∽△ABC
∠AEC=∠ACB, ∠ACE=∠B,
AC
AE
AB
AC
BC
CE
=
=
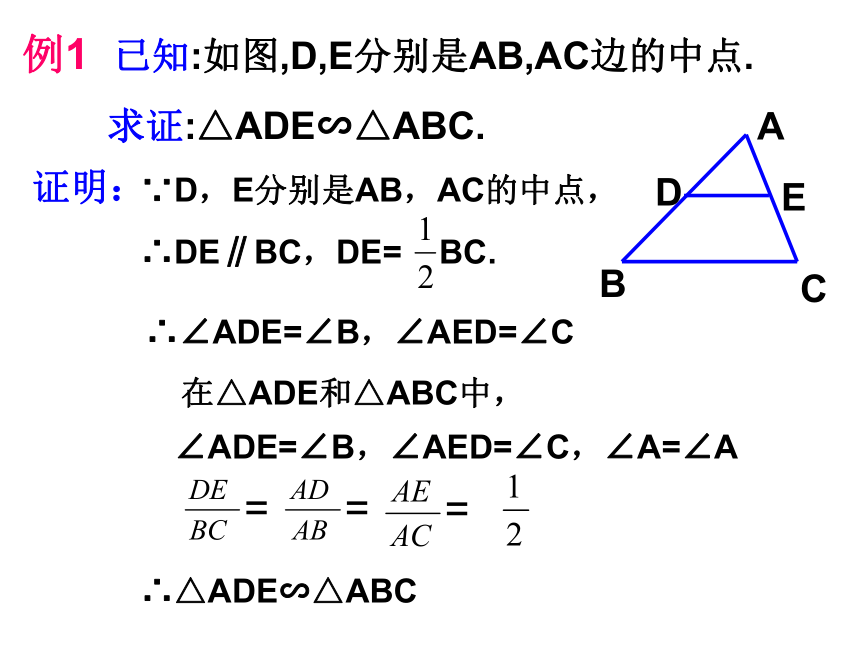
例1 已知:如图,D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.
E
D
C
B
A
证明:
∵D,E分别是AB,AC的中点,
∴∠ADE=∠B,∠AED=∠C
在△ADE和△ABC中,
∠ADE=∠B,∠AED=∠C,∠A=∠A
=
=
=
∴DE∥BC,DE= BC.
∴△ADE∽△ABC
练一练
如图,请你判断△ABC与△A'B'C'相似吗?为什么?
例2、已知:如图,D,E分别是△ABC的AB,AC边上的点, △ABC∽△ADE.已知AD﹕DB=1﹕2,BC=9cm,求DE的长.
E
D
C
B
A
相似三角形对应边的比,叫做两个相似三角形的相似比.
温馨提醒:AD:DB的比是△ADE与△ABC的相似比吗
x
20
33
48
22
30
45°
85°
m°
n°
50°
45°
3a
2a
y
10
变式1、如图(1),D,E分别是△ABC的边AB,AC延长线上的点,点D与点B是对应点. △ ADE ∽△ ABC.已知AD﹕DB=1﹕3,BC=9cm,求DE的长.
变式2:如图(2),D,E分别是△ABC的AB,AC边上的点,△ADE∽△ACB.∠ADE=∠C,
A
E
D
C
B
图1
A
D
E
B
C
图2
AD=2 cm,DB=4 cm,AC=10cm,求AE的长.
1、已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的最大边为8,求其余两边.
2、已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的一边为8,求其余两边.
4和6
4,6 或 12,16 或 16/3,32/3
如图,在Rt△ABC中∠C=900,∠A=300,E为AB上一点,且AE:EB=4:1,EF⊥AC于F,连结FB,求BC:CF
A
B
C
E
F
在△ABC中,AB=m,AC=n,P是AB的中点,过点P的直线交AC于点Q,若以A、P、Q为顶点的三角形与A、B、C为顶点的三角形相似,求AQ的长。
请你谈谈对相似三角形的认识,让大家与你分享吧!
欣赏 观 察
4.3 相似三角形
C
A
B
B′
A′
C′
如图,在方格纸内有两个三角形△ABC和△A ’ B ’ C ’
(设方格纸的每个正方形边长为1)
问题1: △A ’ B ’ C ’ 与△ABC的对应边之间有什么关系?
问题2: △A ’ B ’ C ’ 与△ABC的对应角之间有什么关系?
对应角相等,对应边成比例.
B′
A′
C′
C
A
B
如: △ A′B′C′与△ABC相似,可以记作:
△A′B′C′∽△ABC
注意:在表示三角形相似时,一般对应的字母写在对应的位置上.
几何语言:
∵∠A′=∠A, ∠B′=∠B, ∠C′=∠C,
AB
A′B′
BC
B′C′
AC
A′C′
=
=
∴△A′B′C′∽△ABC
对应角相等,对应边成比例.
判定
B
A
C
B′
A′
C′
相似三角形的对应角相等,对应边成比例.
如图,∵ △A′B′C′∽△ABC
∴ ∠A′=∠A, ∠B′=∠B, ∠C′=∠C,
AB
A′B′
BC
B′C′
AC
A′C′
=
=
注意:两个三角形的顺序不同,相似比也不同.
性质
(4)两个全等三角形一定相似。 ( )
(3)两个等边三角形一定相似。 ( )
(1)两个直角三角形一定相似。 ( )
(2)两个等腰三角形一定相似。 ( )
30
45
(5)两个等腰直角三角形一定相似. ( )
如图,△ADE∽△ABC,根据图形分别说出两个三角形的对应角和对应边成比例的比例式。
A
B
D
E
C
(1)
AB
AD
AC
AE
BC
DE
=
=
∠ADE=∠B, ∠AED=∠C,
∠A=∠A,
∠BAC=∠DAE,
A
B
C
E
D
(2)
△ACE∽△ABC
∠AEC=∠ACB, ∠ACE=∠B,
AC
AE
AB
AC
BC
CE
=
=
例1 已知:如图,D,E分别是AB,AC边的中点.
求证:△ADE∽△ABC.
E
D
C
B
A
证明:
∵D,E分别是AB,AC的中点,
∴∠ADE=∠B,∠AED=∠C
在△ADE和△ABC中,
∠ADE=∠B,∠AED=∠C,∠A=∠A
=
=
=
∴DE∥BC,DE= BC.
∴△ADE∽△ABC
练一练
如图,请你判断△ABC与△A'B'C'相似吗?为什么?
例2、已知:如图,D,E分别是△ABC的AB,AC边上的点, △ABC∽△ADE.已知AD﹕DB=1﹕2,BC=9cm,求DE的长.
E
D
C
B
A
相似三角形对应边的比,叫做两个相似三角形的相似比.
温馨提醒:AD:DB的比是△ADE与△ABC的相似比吗
x
20
33
48
22
30
45°
85°
m°
n°
50°
45°
3a
2a
y
10
变式1、如图(1),D,E分别是△ABC的边AB,AC延长线上的点,点D与点B是对应点. △ ADE ∽△ ABC.已知AD﹕DB=1﹕3,BC=9cm,求DE的长.
变式2:如图(2),D,E分别是△ABC的AB,AC边上的点,△ADE∽△ACB.∠ADE=∠C,
A
E
D
C
B
图1
A
D
E
B
C
图2
AD=2 cm,DB=4 cm,AC=10cm,求AE的长.
1、已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的最大边为8,求其余两边.
2、已知△ABC与△DEF相似, △ABC的三边为2,3,4, △DEF的一边为8,求其余两边.
4和6
4,6 或 12,16 或 16/3,32/3
如图,在Rt△ABC中∠C=900,∠A=300,E为AB上一点,且AE:EB=4:1,EF⊥AC于F,连结FB,求BC:CF
A
B
C
E
F
在△ABC中,AB=m,AC=n,P是AB的中点,过点P的直线交AC于点Q,若以A、P、Q为顶点的三角形与A、B、C为顶点的三角形相似,求AQ的长。
请你谈谈对相似三角形的认识,让大家与你分享吧!
同课章节目录
