第一章 二次函数 章末复习-----符号问题 课件(共18张PPT)
文档属性
| 名称 | 第一章 二次函数 章末复习-----符号问题 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-22 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
第一章 二次函数章末复习
----二次函数中的符号问题
浙教版九年级上册
新知导入
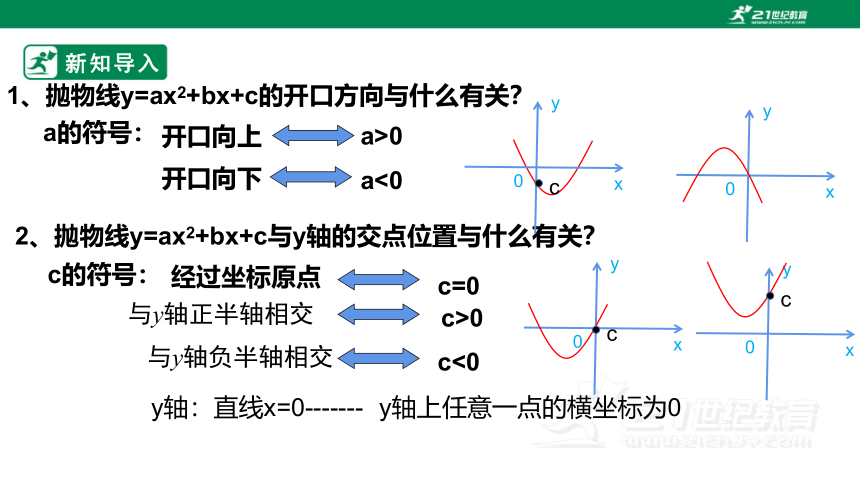
1、抛物线y=ax2+bx+c的开口方向与什么有关?
2、抛物线y=ax2+bx+c与y轴的交点位置与什么有关?
a的符号:
开口向上
a>0
开口向下
a<0
c>0
c的符号:
经过坐标原点
c=0
与y轴正半轴相交
与y轴负半轴相交
c<0
x
0
y
x
0
y
x
0
y
x
0
y
c
c
c
y轴:直线x=0-------
y轴上任意一点的横坐标为0
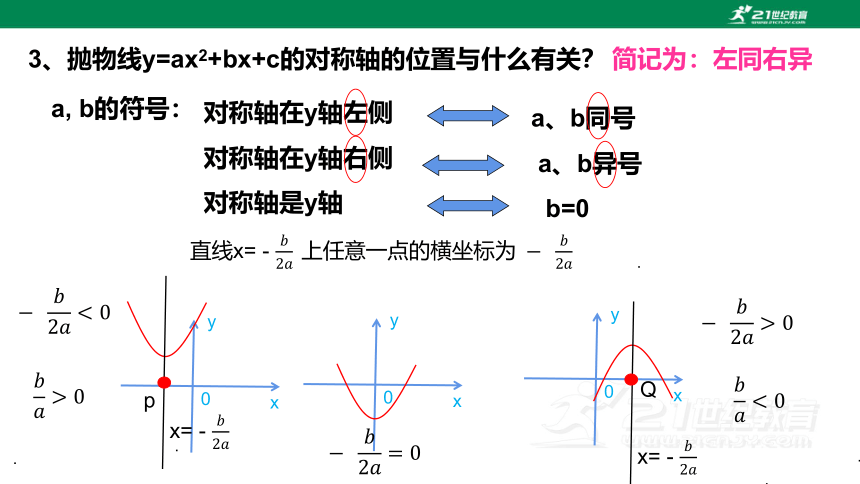
3、抛物线y=ax2+bx+c的对称轴的位置与什么有关?
a, b的符号:
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
简记为:左同右异
x
0
y
x= -
直线x= -
.
p
.
.
x
0
y
x= -
.
.
Q
x
0
y
.
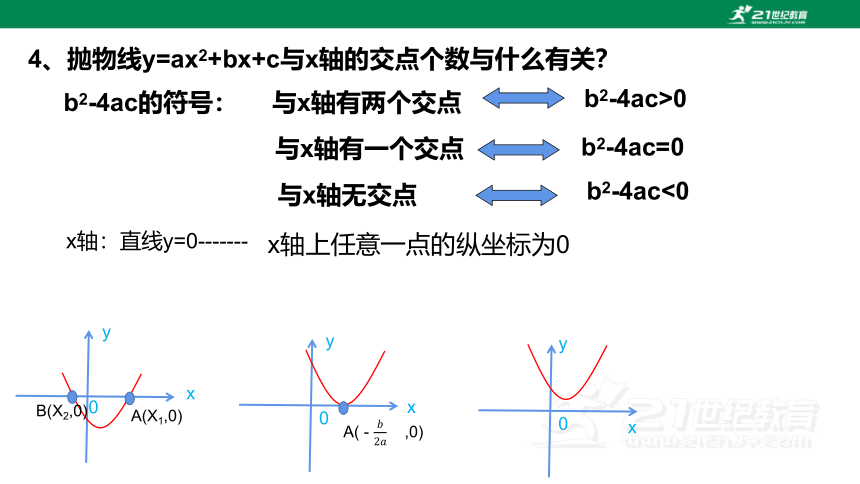
4、抛物线y=ax2+bx+c与x轴的交点个数与什么有关?
x
0
y
x
0
y
x
0
y
b2-4ac的符号:
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
x轴:直线y=0-------
x轴上任意一点的纵坐标为0
A(X1,0)
B(X2,0)
A( - ,0)
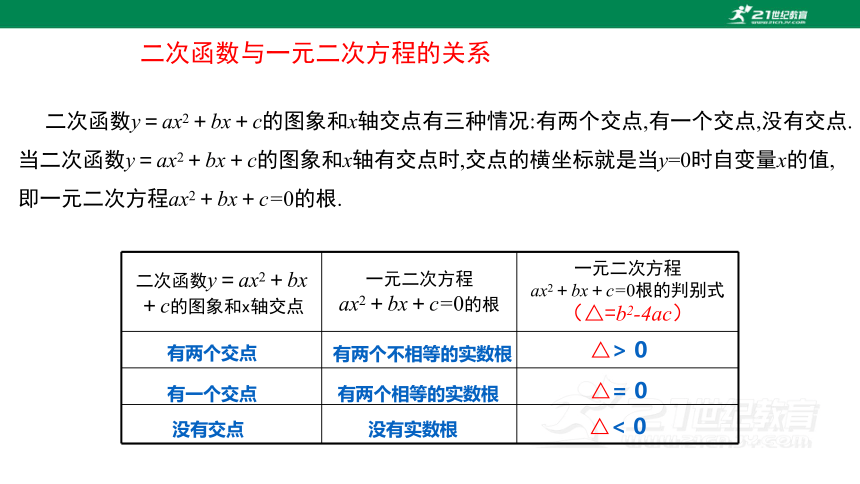
二次函数与一元二次方程的关系
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,
即一元二次方程ax2+bx+c=0的根.
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程 ax2+bx+c=0的根 一元二次方程
ax2+bx+c=0根的判别式(△=b2-4ac)
有两个交点
有两个不相等的实数根
△> 0
有一个交点
有两个相等的实数根
△= 0
没有交点
没有实数根
△< 0
(5)看见 a+b+c:
你想到了什么?
y=ax2+bx+c
a+b+c的符号由x=1时抛物线上的点的位置确定
x
0
y
1
a+b+c
x
0
y
1
a+b+c
看见 a-b+c:
你想到了什么?
a-b+c的符号由x=-1时抛物线上的点的位置确定
x
0
y
-1
a-b+c
x
0
y
-1
a-b+c
p
p
p
p
你还可想到什么?
二次函数 y=ax2+bx+c 的图象特征与系数 a,b,c 的符号之间的关系是互逆的,即由字母的符号能确定图象的特征,反之,根据图象的特征,也可以确定其解析式 y=ax2+bx+c 中系数 a,b,c的符号.
知识小结
字母符号 图象的特征
a>0 开口__________
a<0 开口__________
b=0 对称轴为_____轴
a,b同号 对称轴在y轴的____侧
a,b异号 对称轴在y轴的____侧
c=0 经过原点
c>0 与y轴交于_____半轴
c<0 与y轴交于_____半轴
向上
向下
y
左
右
正
负
夯实基础,稳扎稳打
1.函数y=3x2-1的图象与y轴的交点坐标是( )
A.(0,1) B.(-1,0) C.(0,-1) D.(1,0)
【分析】根据y轴上点的坐标特征,令x=0即可求解.
解:令x=0,则y=-1,
∴函数y=3x2-1的图象与y轴的交点坐标是(0,-1),
C
2.抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
o
y
a>0
b<0
c>0
△>0
开口向上
左同右异
与y轴正半轴相交
与x轴有两个交点
3.抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
开口向下
a<0
左同右异
b<0
经过坐标原点
c=0
与x轴有两个交点
△>0
3.抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
开口向上
a>0
左同右异
b<0
c>0
与x轴有一个交点
△>0
x
y
o
与y轴正半轴相交
4.抛物线y=ax2+bx+c(a≠0) 位置分别如下列四图时,其系数中
的特殊值对应的分别有
_________ _________ __________ __________
x
y
O
①
x
y
O
②
x
y
O
③
x
y
O
④
c=0
b2-4ac =0
b=0
b=c=0
特殊值:
5.如图,若a<0,b>0,c<0,则二次函数y=ax2+bx+c的大致图象为( ).
x
y
O
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
C
交y轴负半轴
开口向下
O
连续递推,豁然开朗
6、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:
①b>0;②c<0;③4a+2b+c < 0;④(a+c)2<b2,
⑤
,m为实数)其中正确的个数是 ( )
A、5个 B、4个
C、3个 D、2个
x
o
y
x=1
A
开口向下
a<0
左同右异
b>0
与y轴负半轴相交
c<0
(a+c)2-b2=(a+c+b)(a+c-b)
a+c-b=a+c+(-b)
-b<0
<0
2
P(2,4a+2b+c)
-
.
b=-2a
4a+2b+c=c<0
a+b+c Q
a+b+c>0
7、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a+b-c<0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个
x
o
y
-1
1
D
开口向下
a<0
左同右异
b<0
与y轴正半轴相交
c>0
-
.
b=2a
a+b+c P
Q a-b+c
8.y=ax2+bx+c(a≠0)函数值恒小于零的条件是____________ ,
并画草图:
思维拓展,更上一层
a<0,
b2-4ac <0
x
y
O
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第一章 二次函数章末复习
----二次函数中的符号问题
浙教版九年级上册
新知导入
1、抛物线y=ax2+bx+c的开口方向与什么有关?
2、抛物线y=ax2+bx+c与y轴的交点位置与什么有关?
a的符号:
开口向上
a>0
开口向下
a<0
c>0
c的符号:
经过坐标原点
c=0
与y轴正半轴相交
与y轴负半轴相交
c<0
x
0
y
x
0
y
x
0
y
x
0
y
c
c
c
y轴:直线x=0-------
y轴上任意一点的横坐标为0
3、抛物线y=ax2+bx+c的对称轴的位置与什么有关?
a, b的符号:
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
简记为:左同右异
x
0
y
x= -
直线x= -
.
p
.
.
x
0
y
x= -
.
.
Q
x
0
y
.
4、抛物线y=ax2+bx+c与x轴的交点个数与什么有关?
x
0
y
x
0
y
x
0
y
b2-4ac的符号:
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
x轴:直线y=0-------
x轴上任意一点的纵坐标为0
A(X1,0)
B(X2,0)
A( - ,0)
二次函数与一元二次方程的关系
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x的值,
即一元二次方程ax2+bx+c=0的根.
二次函数y=ax2+bx+c的图象和x轴交点 一元二次方程 ax2+bx+c=0的根 一元二次方程
ax2+bx+c=0根的判别式(△=b2-4ac)
有两个交点
有两个不相等的实数根
△> 0
有一个交点
有两个相等的实数根
△= 0
没有交点
没有实数根
△< 0
(5)看见 a+b+c:
你想到了什么?
y=ax2+bx+c
a+b+c的符号由x=1时抛物线上的点的位置确定
x
0
y
1
a+b+c
x
0
y
1
a+b+c
看见 a-b+c:
你想到了什么?
a-b+c的符号由x=-1时抛物线上的点的位置确定
x
0
y
-1
a-b+c
x
0
y
-1
a-b+c
p
p
p
p
你还可想到什么?
二次函数 y=ax2+bx+c 的图象特征与系数 a,b,c 的符号之间的关系是互逆的,即由字母的符号能确定图象的特征,反之,根据图象的特征,也可以确定其解析式 y=ax2+bx+c 中系数 a,b,c的符号.
知识小结
字母符号 图象的特征
a>0 开口__________
a<0 开口__________
b=0 对称轴为_____轴
a,b同号 对称轴在y轴的____侧
a,b异号 对称轴在y轴的____侧
c=0 经过原点
c>0 与y轴交于_____半轴
c<0 与y轴交于_____半轴
向上
向下
y
左
右
正
负
夯实基础,稳扎稳打
1.函数y=3x2-1的图象与y轴的交点坐标是( )
A.(0,1) B.(-1,0) C.(0,-1) D.(1,0)
【分析】根据y轴上点的坐标特征,令x=0即可求解.
解:令x=0,则y=-1,
∴函数y=3x2-1的图象与y轴的交点坐标是(0,-1),
C
2.抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
o
y
a>0
b<0
c>0
△>0
开口向上
左同右异
与y轴正半轴相交
与x轴有两个交点
3.抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
开口向下
a<0
左同右异
b<0
经过坐标原点
c=0
与x轴有两个交点
△>0
3.抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
开口向上
a>0
左同右异
b<0
c>0
与x轴有一个交点
△>0
x
y
o
与y轴正半轴相交
4.抛物线y=ax2+bx+c(a≠0) 位置分别如下列四图时,其系数中
的特殊值对应的分别有
_________ _________ __________ __________
x
y
O
①
x
y
O
②
x
y
O
③
x
y
O
④
c=0
b2-4ac =0
b=0
b=c=0
特殊值:
5.如图,若a<0,b>0,c<0,则二次函数y=ax2+bx+c的大致图象为( ).
x
y
O
x
y
O
x
y
O
x
y
O
A.
B.
C.
D.
C
交y轴负半轴
开口向下
O
连续递推,豁然开朗
6、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:
①b>0;②c<0;③4a+2b+c < 0;④(a+c)2<b2,
⑤
,m为实数)其中正确的个数是 ( )
A、5个 B、4个
C、3个 D、2个
x
o
y
x=1
A
开口向下
a<0
左同右异
b>0
与y轴负半轴相交
c<0
(a+c)2-b2=(a+c+b)(a+c-b)
a+c-b=a+c+(-b)
-b<0
<0
2
P(2,4a+2b+c)
-
.
b=-2a
4a+2b+c=c<0
a+b+c Q
a+b+c>0
7、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a+b-c<0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个
x
o
y
-1
1
D
开口向下
a<0
左同右异
b<0
与y轴正半轴相交
c>0
-
.
b=2a
a+b+c P
Q a-b+c
8.y=ax2+bx+c(a≠0)函数值恒小于零的条件是____________ ,
并画草图:
思维拓展,更上一层
a<0,
b2-4ac <0
x
y
O
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
