浙教版数学九年级上册 4.1 比例线段 课件(共17张PPT)
文档属性
| 名称 | 浙教版数学九年级上册 4.1 比例线段 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 409.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 08:35:01 | ||
图片预览






文档简介
(共17张PPT)
a、d 叫做比例外项,
b、c 叫做比例内项,
四个数 a、b、c、d 中,如果
a c
b d
=
(或a:b=c:d),
那么这四个数a、b、 c 、 d 成比例
复习回顾
即:比例的两外项之积等于两内项之积.
比例的基本性质
(a,b,c,d都不为零)
2
(2) x:y:z=2:3:4 ,求 的值.
x-y+z
2x+3y-z
(1) 已知 ,求 的值.
a-b
b
a
b
3
2
=
1、设线段AB=2cm,AC=4cm,
两条线段的长度比是
记作:
2、设线段AB=200cm,AC=4m,
两条线段的长度比是
200:4=
200:400=
两条线段单位要统一
两条线段的长度比叫做这两条线段的比
2:4=
A
B
C
A′
B′
C′
1
1
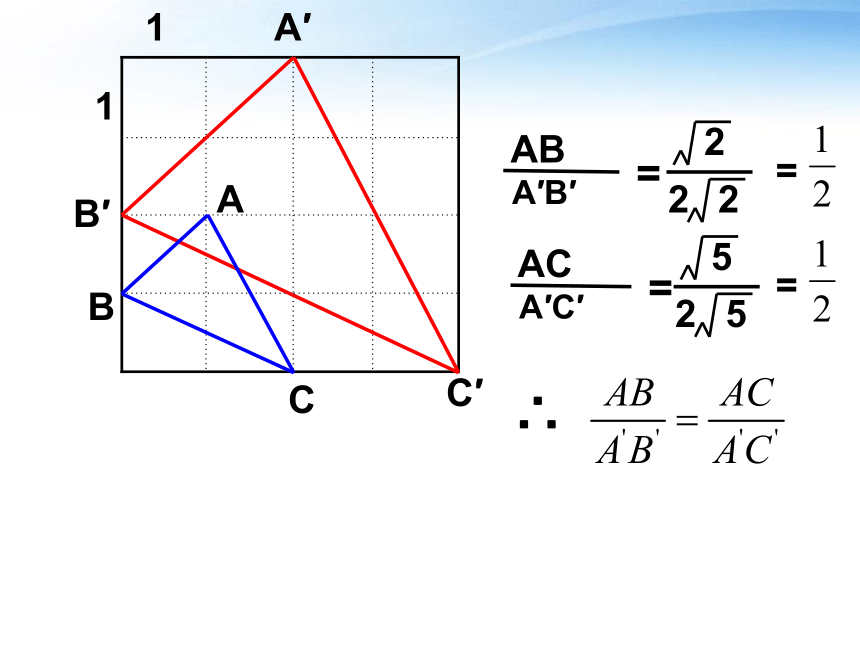
AB
A′B′
=
2
2
2
=
AC
A′C′
=
5
5
2
=
∴
一般地,如果四条线段a,b,c,d中,a与b的比等于c与d的比.即 ,那么这四条线段叫做成比例线段,简称比例线段.
请找出左图的3组比例线段,并写出比例式
A
B
C
A′
B′
1
1
A B
A′B′
=
A C
A′C′
C′
试一试
1、如图,DE是△ABC的中位线,请尽可能多的写出比例线段
E
D
C
B
A
2、已知线段a=10mm,b=6cm,c=2cm,d=3cm,问这四条线段是否成比例?
(1)把四条线段按大小排列好,判断前两条线段的比和后两条
线段的比是否相等.
(2)查看是否有两条线段的积等于其余两条线段的积.
判断四条线段成比例的方法:
例3 如图,在直角三角形ABC中,CD是斜边AB上的高线,请找出一组比例线段,并说明理由
A
B
C
D
根据 ,问题就转化为找出四条线段,使其中2条线段的乘积等于另2条线段的乘积
如图,已知AD,CE是△ABC中BC、AB上的高线.
求证:
如图在平行四边形ABCD中,
d
c
b
a
F
E
D
C
B
A
线段(用小写字母表示)并说明理由.
找出图中的一组比例
A
B
C
D
O
E
如图,在菱形ABCD中,AE⊥BC,
对角线BD与AC交于点O.
试判断线段AE,AO,BD,BC是
否成比例,并说明理由。
已知△ABC的三边比为
三边上的高为
则
已知:A、B两地的实际距离AB=250m
画在地图上的距离
A
'
B
'
=5cm
求图上距离与实际距离的比.
(即该地图的比例尺)
如图是我国台湾省的几个城市的位置图,问基隆市在高雄市的哪个方向?到高雄市的实际距离是多少km?(比例尺1:9000000)
注意:求角度时要注意方位。
解:从图上量出高雄市到基隆市的距离约35mm,设实际距离为s,则
35
s
=
1
9000000
∴S=35×9000000=315000000(mm)
即s=315(km)
量得图中∠1=28°.
答:基隆市在高雄市的北偏东28°方向,到高雄市的实际距离约为315km。
北
高雄
台南
台中
台北
基隆
现在有一棵很高的古树,欲测出它的高度,但又不能爬到树尖上去直接测量,你有什么好的方法吗?
动动脑筋
A
B
C
A’
B’
C’
a、d 叫做比例外项,
b、c 叫做比例内项,
四个数 a、b、c、d 中,如果
a c
b d
=
(或a:b=c:d),
那么这四个数a、b、 c 、 d 成比例
复习回顾
即:比例的两外项之积等于两内项之积.
比例的基本性质
(a,b,c,d都不为零)
2
(2) x:y:z=2:3:4 ,求 的值.
x-y+z
2x+3y-z
(1) 已知 ,求 的值.
a-b
b
a
b
3
2
=
1、设线段AB=2cm,AC=4cm,
两条线段的长度比是
记作:
2、设线段AB=200cm,AC=4m,
两条线段的长度比是
200:4=
200:400=
两条线段单位要统一
两条线段的长度比叫做这两条线段的比
2:4=
A
B
C
A′
B′
C′
1
1
AB
A′B′
=
2
2
2
=
AC
A′C′
=
5
5
2
=
∴
一般地,如果四条线段a,b,c,d中,a与b的比等于c与d的比.即 ,那么这四条线段叫做成比例线段,简称比例线段.
请找出左图的3组比例线段,并写出比例式
A
B
C
A′
B′
1
1
A B
A′B′
=
A C
A′C′
C′
试一试
1、如图,DE是△ABC的中位线,请尽可能多的写出比例线段
E
D
C
B
A
2、已知线段a=10mm,b=6cm,c=2cm,d=3cm,问这四条线段是否成比例?
(1)把四条线段按大小排列好,判断前两条线段的比和后两条
线段的比是否相等.
(2)查看是否有两条线段的积等于其余两条线段的积.
判断四条线段成比例的方法:
例3 如图,在直角三角形ABC中,CD是斜边AB上的高线,请找出一组比例线段,并说明理由
A
B
C
D
根据 ,问题就转化为找出四条线段,使其中2条线段的乘积等于另2条线段的乘积
如图,已知AD,CE是△ABC中BC、AB上的高线.
求证:
如图在平行四边形ABCD中,
d
c
b
a
F
E
D
C
B
A
线段(用小写字母表示)并说明理由.
找出图中的一组比例
A
B
C
D
O
E
如图,在菱形ABCD中,AE⊥BC,
对角线BD与AC交于点O.
试判断线段AE,AO,BD,BC是
否成比例,并说明理由。
已知△ABC的三边比为
三边上的高为
则
已知:A、B两地的实际距离AB=250m
画在地图上的距离
A
'
B
'
=5cm
求图上距离与实际距离的比.
(即该地图的比例尺)
如图是我国台湾省的几个城市的位置图,问基隆市在高雄市的哪个方向?到高雄市的实际距离是多少km?(比例尺1:9000000)
注意:求角度时要注意方位。
解:从图上量出高雄市到基隆市的距离约35mm,设实际距离为s,则
35
s
=
1
9000000
∴S=35×9000000=315000000(mm)
即s=315(km)
量得图中∠1=28°.
答:基隆市在高雄市的北偏东28°方向,到高雄市的实际距离约为315km。
北
高雄
台南
台中
台北
基隆
现在有一棵很高的古树,欲测出它的高度,但又不能爬到树尖上去直接测量,你有什么好的方法吗?
动动脑筋
A
B
C
A’
B’
C’
同课章节目录
