浙教版数学七年级上册 2.1 有理数的加法 课件(共14张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 2.1 有理数的加法 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 132.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 09:36:46 | ||
图片预览





文档简介
(共14张PPT)
2.1.2 有理数的加法
知识回顾
有理数加法计算的一般步骤:
一观察、二定号、三求值
小学学过哪些加法的运算律:
加法交换律、加法结合律
数扩展到有理数后,下面这些结论还成立吗?请说明理由(如果认为结论不成立,请举例说明).
若两个数的和是0,则这两个数都是0.
任何两数相加,和不小于任何一个加数.
思考:小学学过的加法运算律在有理数范围内仍然适用吗?
探究
获取新知
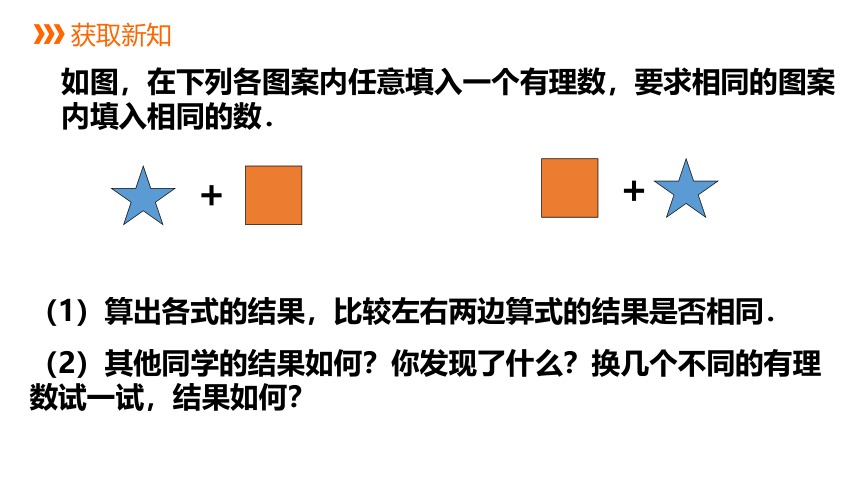
如图,在下列各图案内任意填入一个有理数,要求相同的图案内填入相同的数.
+
+
(1)算出各式的结果,比较左右两边算式的结果是否相同.
(2)其他同学的结果如何?你发现了什么?换几个不同的有理数试一试,结果如何?
加法交换律:
两个数相加,交换加数的位置,和不变.
a+b=b+a
归纳总结
获取新知
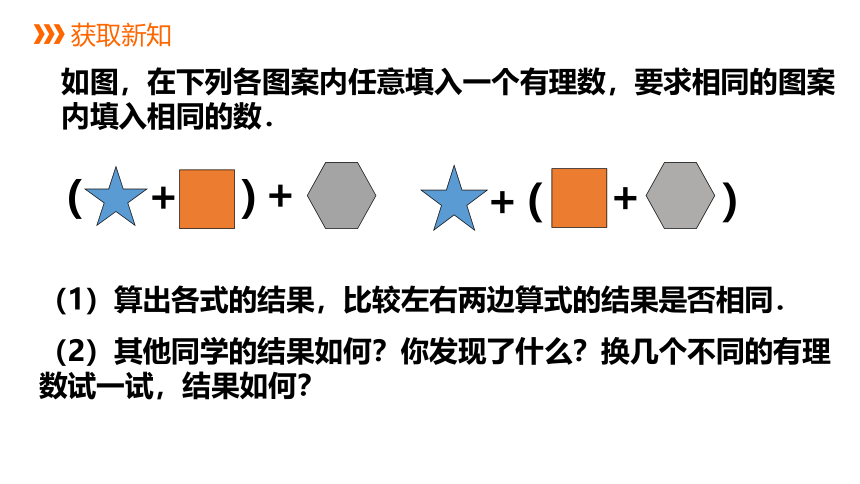
如图,在下列各图案内任意填入一个有理数,要求相同的图案内填入相同的数.
+
+
(
)
+
+
(
)
(1)算出各式的结果,比较左右两边算式的结果是否相同.
(2)其他同学的结果如何?你发现了什么?换几个不同的有理数试一试,结果如何?
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
(a+b)+c=a+(b+c)
更一般地,任意若干个数相加,无论各数相加的先后次序如何,其和都不变.
归纳总结
例3 计算:
(1)15+(-13)+18;
(2)(-2.48)+4.33+(-7.52)+(-4.33);
(3) .
例题精讲
解:(1)原式=15+18+(-13)
=33+(-13)
=20
=(15+18)+(-13)
加法交换律
加法结合律
同号结合
例题精讲
(2)原式=(-2.48)+(-7.52)+(+4.33)+(-4.33)
=[(-2.48)+(-7.52)]+[(+4.33)+(-4.33)]
=(-10)+0
=-10
(3)原式=
=
=
能凑整的数结合
相反数结合
同分母的数结合
随堂演练
练习:用简便方法计算,并说明相关理由
例4 小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15 m,再向西行驶25 m,然后又向东行驶20 m,再向西行驶35 m,问玩具赛车最后停在何处?一共行驶了多少米?
A
-25 -20 -15 -10 -5 0 5 10 15
东
西
+15
-25
-35
+20
解:规定向东行驶为正.
(+15)+(-25)+(+20)+(-35)
=(15+20)+[(-25)+(-35)]=35+(-60)=-25(m);
答:小明的遥控车最后停在小明的西边25 m处,一共行驶了95 m.
|+15|+|-25|+|+20|+|-35|
=15+25+20+35=95(m).
练习1:已知有6筐蔬菜,以每筐50千克为基准,超过的千克数记为正数,不足的千克数记为负数,记录如下(单位:千克):
-2;+2;+3;-0.5;+4;-3.5.
那么这6筐蔬菜的总质量是 ( )
A. 300千克 B. 302千克
C. 303千克 D. 305千克
练习2:今有10包盐过磅验收,称得各包质量如下(单位:千克)
202 , 204 , 200 , 201 ,203,
198 , 202 , 199 , 197 ,204
求这10包盐的总质量.
2.1.2 有理数的加法
知识回顾
有理数加法计算的一般步骤:
一观察、二定号、三求值
小学学过哪些加法的运算律:
加法交换律、加法结合律
数扩展到有理数后,下面这些结论还成立吗?请说明理由(如果认为结论不成立,请举例说明).
若两个数的和是0,则这两个数都是0.
任何两数相加,和不小于任何一个加数.
思考:小学学过的加法运算律在有理数范围内仍然适用吗?
探究
获取新知
如图,在下列各图案内任意填入一个有理数,要求相同的图案内填入相同的数.
+
+
(1)算出各式的结果,比较左右两边算式的结果是否相同.
(2)其他同学的结果如何?你发现了什么?换几个不同的有理数试一试,结果如何?
加法交换律:
两个数相加,交换加数的位置,和不变.
a+b=b+a
归纳总结
获取新知
如图,在下列各图案内任意填入一个有理数,要求相同的图案内填入相同的数.
+
+
(
)
+
+
(
)
(1)算出各式的结果,比较左右两边算式的结果是否相同.
(2)其他同学的结果如何?你发现了什么?换几个不同的有理数试一试,结果如何?
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
(a+b)+c=a+(b+c)
更一般地,任意若干个数相加,无论各数相加的先后次序如何,其和都不变.
归纳总结
例3 计算:
(1)15+(-13)+18;
(2)(-2.48)+4.33+(-7.52)+(-4.33);
(3) .
例题精讲
解:(1)原式=15+18+(-13)
=33+(-13)
=20
=(15+18)+(-13)
加法交换律
加法结合律
同号结合
例题精讲
(2)原式=(-2.48)+(-7.52)+(+4.33)+(-4.33)
=[(-2.48)+(-7.52)]+[(+4.33)+(-4.33)]
=(-10)+0
=-10
(3)原式=
=
=
能凑整的数结合
相反数结合
同分母的数结合
随堂演练
练习:用简便方法计算,并说明相关理由
例4 小明遥控一辆玩具赛车,让它从A地出发,先向东行驶15 m,再向西行驶25 m,然后又向东行驶20 m,再向西行驶35 m,问玩具赛车最后停在何处?一共行驶了多少米?
A
-25 -20 -15 -10 -5 0 5 10 15
东
西
+15
-25
-35
+20
解:规定向东行驶为正.
(+15)+(-25)+(+20)+(-35)
=(15+20)+[(-25)+(-35)]=35+(-60)=-25(m);
答:小明的遥控车最后停在小明的西边25 m处,一共行驶了95 m.
|+15|+|-25|+|+20|+|-35|
=15+25+20+35=95(m).
练习1:已知有6筐蔬菜,以每筐50千克为基准,超过的千克数记为正数,不足的千克数记为负数,记录如下(单位:千克):
-2;+2;+3;-0.5;+4;-3.5.
那么这6筐蔬菜的总质量是 ( )
A. 300千克 B. 302千克
C. 303千克 D. 305千克
练习2:今有10包盐过磅验收,称得各包质量如下(单位:千克)
202 , 204 , 200 , 201 ,203,
198 , 202 , 199 , 197 ,204
求这10包盐的总质量.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
