浙教版七年级上册 3.3 立方根 课件 16张PPT
文档属性
| 名称 | 浙教版七年级上册 3.3 立方根 课件 16张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 360.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 09:07:07 | ||
图片预览





文档简介
(共16张PPT)
3.3 立方根
问题引入,章节起始
∵( ±2 )2=4
∵23=8
立 方 根
你能类比平方根的定义,给立方根也下一个定义吗?
∴±2是4的平方根
∴2是8的 。
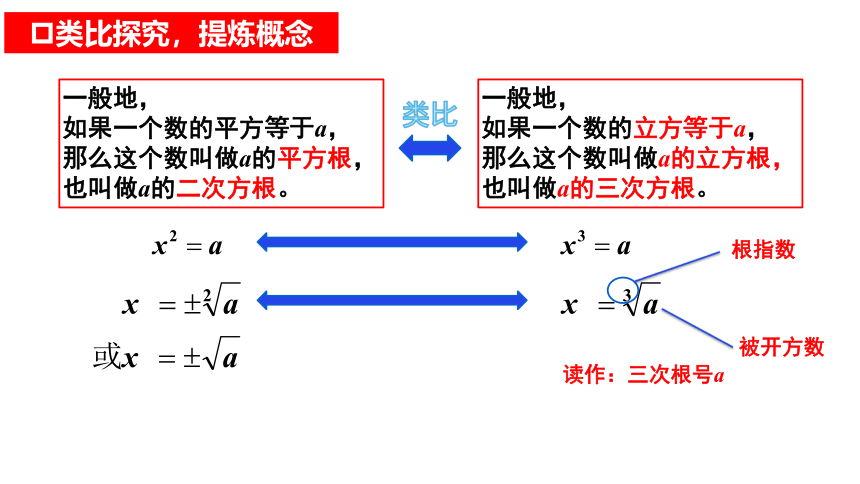
类比探究,提炼概念
一般地,
如果一个数的平方等于a,
那么这个数叫做a的平方根,
也叫做a的二次方根。
一般地,
如果一个数的立方等于a,
那么这个数叫做a的立方根,
也叫做a的三次方根。
类比
根指数
被开方数
读作:三次根号a
深入探究,明确概念
【问题】: 的被开方数、根指数、结果分别是多少?
求一个数的立方根的运算,叫做开立方。
立方和开立方运算,互为逆运算。
深入探究,形成概念
例1 求下列各数的立方根:
(1) 27 (2)-27
如何求一个数的立方根呢?
思考:
开平方运算
平方运算
互逆
平方运算
平方根
类比
开立方运算
立方运算
互逆
立方运算
立方根
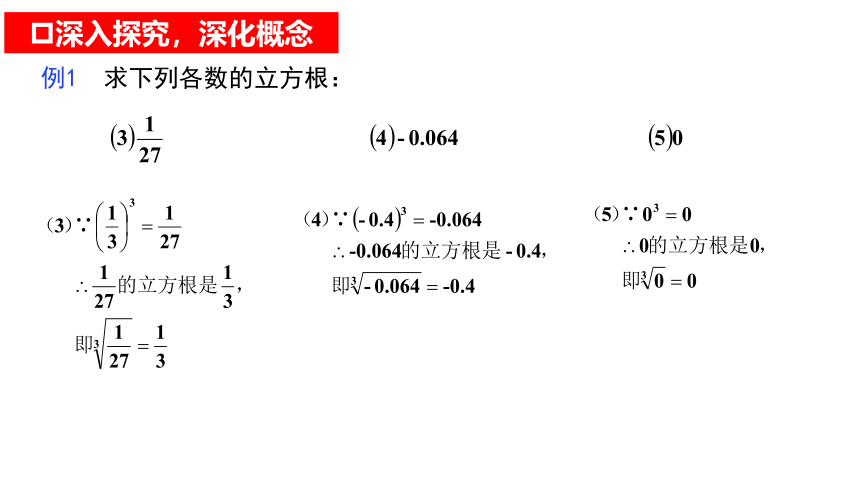
深入探究,深化概念
例1 求下列各数的立方根:
例题演练,掌握新知
比较归纳1
互为相反数的两个数的立方根也互为相反数
互为倒数的两个数的立方根也互为倒数
思考: 立方根等于它本身的数有哪些?
0,1,-1
深入拓展,体悟新知
比较归纳2
一个正数有几个立方根?符号是什么呢?
一个负数有几个立方根?符号又是什么呢?
1
正
1
负
深化拓展,体悟新知
立方根的性质:
一个正数有一个正的立方根;一个负数有一个负的立方根;
0的立方根是0。
发现:任意一个实数都有一个立方根
比一比
与平方根的性质比较有哪些相同与不同之处呢?
不同:
①负数没有平方根,但任意实数都有立方根
②一个正数有正、负两个平方根,而正数的立方根只有一个。
相同:
0的平方根和立方根都是0
深化拓展,体悟新知
判断下列说法是否正确,并说明理由:
(1)8的立方根是±2.
×
辨一辨
(2)负数不能开立方.
(3)一个数的立方和它的立方根
不可能相等.
(4)一个数的立方和它的平方根
不可能相等.
一个正数只有一个正的立方根
×
一个负数有一个负的立方根
×
例如:1的立方和立方根都是1
×
例如:0的立方根和平方根都是0
例题演练,掌握新知
例2 计算:
深化拓展,体悟新知
练一练:计算下列各式的值:
=6
=-0.2
=-2-5
=-7
=0.1+0.1
=0.2
深化拓展,体悟新知
拓展1:把一个长、宽、高分别为50cm、8cm、20cm的铁块锻造成
一个立方体铁块,则立方体铁块的棱长为多少?
等量关系
∵ V前=V后
∴V后=50×8×20=8000cm3
解:设立方体铁块的棱长为xcm
x3=8000
答:立方体铁块的棱长为20cm
深化拓展,体悟新知
拓展2:已知a,b都是整数,且满足 。
请写出一对符合条件的a,b的值。
①等式右边是个有理数,则等式左边也必定是个有理数,所以 和 都是开方开的尽的数。
②右边是一个负数,而 ≥0,则 <0,所以a≥0,b<0。
③可以先确定其中一个字母的值,比如先确定a,然后求出b的值。
思考:我们可以取a等于几呢?
满足 开方开的尽的整数。按有序思考的习惯,可以先取a能取到的最小整数0,然后再依次增大a的取值。
深化拓展,体悟新知
拓展2:已知a,b都是整数,且满足 。
请写出一对符合条件的a,b的值。
0
0
-2
-8
1
1
-3
-27
4
2
-4
-64
9
3
-5
-125
…
…
…
…
小结新课,梳理新知
知识点
方法技能:
数学思想:
立方根的概念:
立方根的性质:
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根,记做 。
一个正数有一个正的立方根;一个负数有一个负的立方根;0的立方根是0。
用立方运算求一个数的立方根。
类比思想
3.3 立方根
问题引入,章节起始
∵( ±2 )2=4
∵23=8
立 方 根
你能类比平方根的定义,给立方根也下一个定义吗?
∴±2是4的平方根
∴2是8的 。
类比探究,提炼概念
一般地,
如果一个数的平方等于a,
那么这个数叫做a的平方根,
也叫做a的二次方根。
一般地,
如果一个数的立方等于a,
那么这个数叫做a的立方根,
也叫做a的三次方根。
类比
根指数
被开方数
读作:三次根号a
深入探究,明确概念
【问题】: 的被开方数、根指数、结果分别是多少?
求一个数的立方根的运算,叫做开立方。
立方和开立方运算,互为逆运算。
深入探究,形成概念
例1 求下列各数的立方根:
(1) 27 (2)-27
如何求一个数的立方根呢?
思考:
开平方运算
平方运算
互逆
平方运算
平方根
类比
开立方运算
立方运算
互逆
立方运算
立方根
深入探究,深化概念
例1 求下列各数的立方根:
例题演练,掌握新知
比较归纳1
互为相反数的两个数的立方根也互为相反数
互为倒数的两个数的立方根也互为倒数
思考: 立方根等于它本身的数有哪些?
0,1,-1
深入拓展,体悟新知
比较归纳2
一个正数有几个立方根?符号是什么呢?
一个负数有几个立方根?符号又是什么呢?
1
正
1
负
深化拓展,体悟新知
立方根的性质:
一个正数有一个正的立方根;一个负数有一个负的立方根;
0的立方根是0。
发现:任意一个实数都有一个立方根
比一比
与平方根的性质比较有哪些相同与不同之处呢?
不同:
①负数没有平方根,但任意实数都有立方根
②一个正数有正、负两个平方根,而正数的立方根只有一个。
相同:
0的平方根和立方根都是0
深化拓展,体悟新知
判断下列说法是否正确,并说明理由:
(1)8的立方根是±2.
×
辨一辨
(2)负数不能开立方.
(3)一个数的立方和它的立方根
不可能相等.
(4)一个数的立方和它的平方根
不可能相等.
一个正数只有一个正的立方根
×
一个负数有一个负的立方根
×
例如:1的立方和立方根都是1
×
例如:0的立方根和平方根都是0
例题演练,掌握新知
例2 计算:
深化拓展,体悟新知
练一练:计算下列各式的值:
=6
=-0.2
=-2-5
=-7
=0.1+0.1
=0.2
深化拓展,体悟新知
拓展1:把一个长、宽、高分别为50cm、8cm、20cm的铁块锻造成
一个立方体铁块,则立方体铁块的棱长为多少?
等量关系
∵ V前=V后
∴V后=50×8×20=8000cm3
解:设立方体铁块的棱长为xcm
x3=8000
答:立方体铁块的棱长为20cm
深化拓展,体悟新知
拓展2:已知a,b都是整数,且满足 。
请写出一对符合条件的a,b的值。
①等式右边是个有理数,则等式左边也必定是个有理数,所以 和 都是开方开的尽的数。
②右边是一个负数,而 ≥0,则 <0,所以a≥0,b<0。
③可以先确定其中一个字母的值,比如先确定a,然后求出b的值。
思考:我们可以取a等于几呢?
满足 开方开的尽的整数。按有序思考的习惯,可以先取a能取到的最小整数0,然后再依次增大a的取值。
深化拓展,体悟新知
拓展2:已知a,b都是整数,且满足 。
请写出一对符合条件的a,b的值。
0
0
-2
-8
1
1
-3
-27
4
2
-4
-64
9
3
-5
-125
…
…
…
…
小结新课,梳理新知
知识点
方法技能:
数学思想:
立方根的概念:
立方根的性质:
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根,记做 。
一个正数有一个正的立方根;一个负数有一个负的立方根;0的立方根是0。
用立方运算求一个数的立方根。
类比思想
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
