浙教版七年级上册 第四章 代数式 复习课件(共16张PPT)
文档属性
| 名称 | 浙教版七年级上册 第四章 代数式 复习课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 825.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
“从古埃及人和巴比伦人开始直到韦达和笛卡尔之前,没有一个数学家能意识到字母可用来表示数。”
——M.克莱因
第4章 代数式(复习课)
题组回顾
③水笔每支m元,铅笔每支n元,小明买了3支水笔和2支铅笔,共花费 元.
②x的3倍除以y所得的商 ;
(1)用代数式表示下列各式
①a的1 倍与2的差 ;
(3m+2n)
请再说出一个代数式“3m+2n”表示的实际意义
题组回顾
整式:①③④⑤⑥
(2)找出下列各式中的整式(用序号表示).
① ② ③3m+2n
④ ⑤ ⑥
哪些是单项式?哪些是多项式?你是如何区分的?
其中单项式:④⑤
多项式:①③⑥
题组回顾
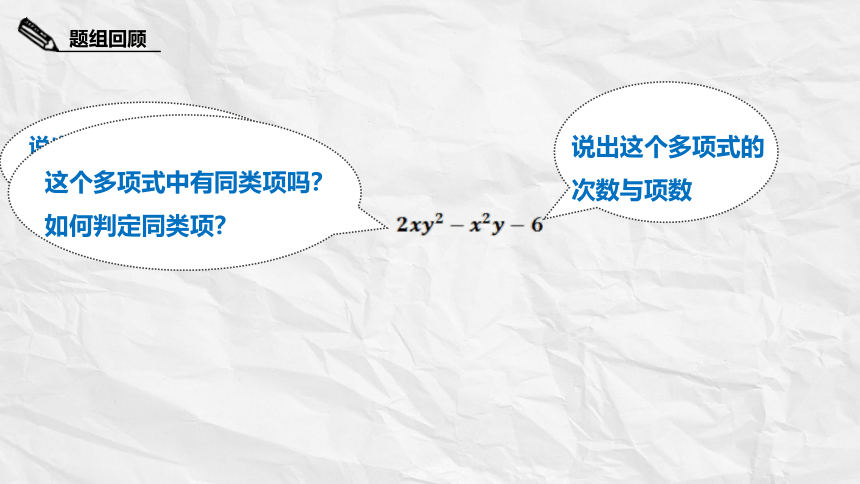
说出这个单项式的系数与次数,你是如何确定的?
说出这个多项式的次数与项数
这个多项式中有同类项吗?
如何判定同类项?
题组回顾
(3)计算 ,并求当 , 时这个代数式的值.
你能由此归纳出整式加减的一般步骤吗?
初理构建
用字母表示数
代数式
列代数式
求代数式值
整式
单项式
多项式
合并同类项
去括号
整式加减运算
(1)用代数式表示下列各式
(2)找出下列各式中的整式(用序号表示)等
(3)计算代数式,并求代数式的值
初理构建
不等关系
不等式的性质
一元一次不等式
应用不等式解决简单实际问题
合并同类项
去括号
不等式
在数轴上表示不等式的解
错题反思
(1)错因诊断
错题反思
(2)症状识别
错题反思
(3)错理分析
典例提升
例1 按照如图所示的操作步骤,若输入x的值为2,则输出的值为 .
变式1 若 ,则多项式 的值是 .
变式2 若代数式 的值为 ,那么代数式 的
值是多少?
典例提升
请把你的出生月份数乘2,加10,把所得的和乘5,再加上你家的人口数(小于10),将计算结果告诉老师,老师就能猜出你家的人口数。
你能用本章代数式的知识来解释这个游戏的原理吗?
本节课收获了什么?
再理总结
(3)解数学题时概念要清楚、结果要规范,要注意过程符合算理、解法的多元性
(1)梳理代数式相关知识点,构建知识结构图
(2)体会了整体思想及特殊与一般的关系
谢谢!
纵观历史,数学的发展创造了数学符号,新的数学符号的使用又反过来促进数学的发展。历史上的数学是这样一步步走过来的,并且需要这样一步步继续走下去,而它的每一个进步都必将伴随着新的数学符号的产生!
我们学习数学亦如此,需要如这节课所做的这样一步步踏踏实实走下去!
思考:
判定一个自然数能否被3整除,只要看这个自然数的各位数字之和是否会被3整除,你能用代数式的知识来解释这个道理吗?
“从古埃及人和巴比伦人开始直到韦达和笛卡尔之前,没有一个数学家能意识到字母可用来表示数。”
——M.克莱因
第4章 代数式(复习课)
题组回顾
③水笔每支m元,铅笔每支n元,小明买了3支水笔和2支铅笔,共花费 元.
②x的3倍除以y所得的商 ;
(1)用代数式表示下列各式
①a的1 倍与2的差 ;
(3m+2n)
请再说出一个代数式“3m+2n”表示的实际意义
题组回顾
整式:①③④⑤⑥
(2)找出下列各式中的整式(用序号表示).
① ② ③3m+2n
④ ⑤ ⑥
哪些是单项式?哪些是多项式?你是如何区分的?
其中单项式:④⑤
多项式:①③⑥
题组回顾
说出这个单项式的系数与次数,你是如何确定的?
说出这个多项式的次数与项数
这个多项式中有同类项吗?
如何判定同类项?
题组回顾
(3)计算 ,并求当 , 时这个代数式的值.
你能由此归纳出整式加减的一般步骤吗?
初理构建
用字母表示数
代数式
列代数式
求代数式值
整式
单项式
多项式
合并同类项
去括号
整式加减运算
(1)用代数式表示下列各式
(2)找出下列各式中的整式(用序号表示)等
(3)计算代数式,并求代数式的值
初理构建
不等关系
不等式的性质
一元一次不等式
应用不等式解决简单实际问题
合并同类项
去括号
不等式
在数轴上表示不等式的解
错题反思
(1)错因诊断
错题反思
(2)症状识别
错题反思
(3)错理分析
典例提升
例1 按照如图所示的操作步骤,若输入x的值为2,则输出的值为 .
变式1 若 ,则多项式 的值是 .
变式2 若代数式 的值为 ,那么代数式 的
值是多少?
典例提升
请把你的出生月份数乘2,加10,把所得的和乘5,再加上你家的人口数(小于10),将计算结果告诉老师,老师就能猜出你家的人口数。
你能用本章代数式的知识来解释这个游戏的原理吗?
本节课收获了什么?
再理总结
(3)解数学题时概念要清楚、结果要规范,要注意过程符合算理、解法的多元性
(1)梳理代数式相关知识点,构建知识结构图
(2)体会了整体思想及特殊与一般的关系
谢谢!
纵观历史,数学的发展创造了数学符号,新的数学符号的使用又反过来促进数学的发展。历史上的数学是这样一步步走过来的,并且需要这样一步步继续走下去,而它的每一个进步都必将伴随着新的数学符号的产生!
我们学习数学亦如此,需要如这节课所做的这样一步步踏踏实实走下去!
思考:
判定一个自然数能否被3整除,只要看这个自然数的各位数字之和是否会被3整除,你能用代数式的知识来解释这个道理吗?
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
