浙教版八年级下册 6.1.1 反比例函数的概念 课件(共15张PPT)
文档属性
| 名称 | 浙教版八年级下册 6.1.1 反比例函数的概念 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 18:12:59 | ||
图片预览






文档简介
(共15张PPT)
6.1.1 反比例函数的概念
在某一变化过程中,不断变化的数量叫变量
保持不变的量叫常量.
变量与常量
回顾与思考
函数
一般地,在某个变化中,有两个变量x和y,如果
给定一个x的值,相应地就确定了y的一个值,那
么我们称y是x的函数
一次函数
y=kx+b(k,b是常数,k≠0)的形式,则称y是
做x的一次函数
y=kx(k是常数,k≠0),称y是x的正比例函数
函数的实质是两个变量之间的关系.
长方形的面积为6 cm ,长为x cm,宽为y cm。
x y =6
问题情境1
②y与x成什么比例关系?
长(单位:cm) 1 2 3 4 5
宽(单位:cm)
6
3
2
1.5
1.2
①完成表格:
③能用一个数学解析式表示吗?
成反比例关系
活动2:
问题2:北京到杭州铁路线长为1661km。一列火车从北京开往杭州,记火车全程的行驶时间为x(h),火车行驶的平均速度为y(km/h), (1)你能完成下列表格吗?
x(h) 12 15 17 22
y(km/h) 87.4
(2) y与x成什么比例关系?
能用一个数学解析式表示吗?
138.4
97.7
110.7
75.5
19
成反比例关系
x y =1661
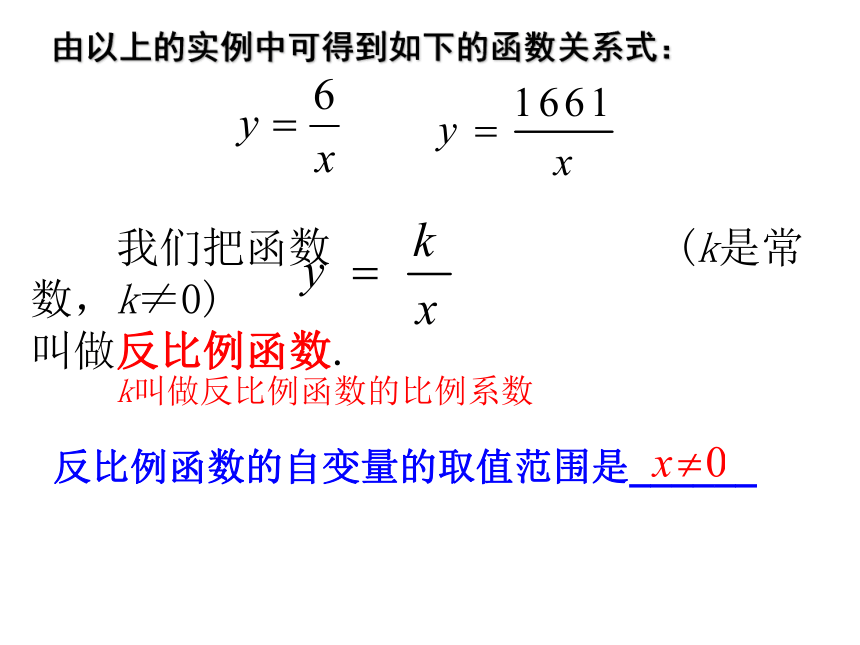
由以上的实例中可得到如下的函数关系式:
我们把函数 (k是常数,k≠0)
叫做反比例函数.
k叫做反比例函数的比例系数
反比例函数的自变量的取值范围是______
1.下列函数中哪些是反比例函数?
① ② ③ ④
y = 3x-1
y = 2x2
y =
2x
3
y =
x
1
2.下列函数中哪些是反比例函数?若是,请指出K的值。
熟悉反比例函数
(7) y=x-1
反比例函数的变形形式:
是反比例函数时,
4.当函数
m= 。
-3
反比例函数的变形形式:
是反比例函数时,
5.当函数
m= 。
-3
2、写出下列各题的函数关系式,指出函数的类型:
(1)正方形的周长C和它的一边的长a之间的关系.
(2)矩形的面积为10时,它的宽y和长x之间的关系.
C=4a
是正比例函数
是反比例函数
是正比例函数
是反比例函数
(3)运动会的田径比赛中,运动员小王的平均速度
是8米/秒,他所跑过的路程S和所用时间t之间的
关系.
(4)王师傅要生产100个零件,他的工作效率P和工
作时间t之间的关系.
S=8t
3. 已知反比例函数y= .
(1)说出这个函数的比例系数和自变量的取值范围.
比例系数为-12,自变量的取值范围为x≠0
当x=-3时,y=4
(3)求当y=- 时自变量x的值.
(2)求当x=-3时函数的值.
4. 设面积为10cm2的三角形的一条边长为a(cm),这条边上的高线长为h(cm).
(1)求h关于a的函数表达式和自变量a的取值范围.
(1)h关于a的函数表达 ,自变量a的取值范围是a>0
(2)h是关于a的反比例函数,比例系数是20
(3)当a=2.5cm时,h=8cm
(2)h关于a的函数是不是反比例函数 如果是,请说出它的比例系数.
(3)求当边长a=2.5cm时,这条边上的高线长.
给我一个支点,我可以撬动地球!
——阿基米德
背景知识
阻力臂
阻力
动力臂
动力
背景知识
杠杆定律
【例1】如图,阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(图中杠杆本身所受重力略去不计。杠杆平衡时:动力×动力臂=阻力×阻力臂)
(1)求y关于x的函数解析式。这个函数是反比例函数吗 如果是,请说出比例系数;
(2)求当x=50时,函数y的值,并说明这个值的实际意义;
(3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n倍时,所需动力将怎样变化?
6.1.1 反比例函数的概念
在某一变化过程中,不断变化的数量叫变量
保持不变的量叫常量.
变量与常量
回顾与思考
函数
一般地,在某个变化中,有两个变量x和y,如果
给定一个x的值,相应地就确定了y的一个值,那
么我们称y是x的函数
一次函数
y=kx+b(k,b是常数,k≠0)的形式,则称y是
做x的一次函数
y=kx(k是常数,k≠0),称y是x的正比例函数
函数的实质是两个变量之间的关系.
长方形的面积为6 cm ,长为x cm,宽为y cm。
x y =6
问题情境1
②y与x成什么比例关系?
长(单位:cm) 1 2 3 4 5
宽(单位:cm)
6
3
2
1.5
1.2
①完成表格:
③能用一个数学解析式表示吗?
成反比例关系
活动2:
问题2:北京到杭州铁路线长为1661km。一列火车从北京开往杭州,记火车全程的行驶时间为x(h),火车行驶的平均速度为y(km/h), (1)你能完成下列表格吗?
x(h) 12 15 17 22
y(km/h) 87.4
(2) y与x成什么比例关系?
能用一个数学解析式表示吗?
138.4
97.7
110.7
75.5
19
成反比例关系
x y =1661
由以上的实例中可得到如下的函数关系式:
我们把函数 (k是常数,k≠0)
叫做反比例函数.
k叫做反比例函数的比例系数
反比例函数的自变量的取值范围是______
1.下列函数中哪些是反比例函数?
① ② ③ ④
y = 3x-1
y = 2x2
y =
2x
3
y =
x
1
2.下列函数中哪些是反比例函数?若是,请指出K的值。
熟悉反比例函数
(7) y=x-1
反比例函数的变形形式:
是反比例函数时,
4.当函数
m= 。
-3
反比例函数的变形形式:
是反比例函数时,
5.当函数
m= 。
-3
2、写出下列各题的函数关系式,指出函数的类型:
(1)正方形的周长C和它的一边的长a之间的关系.
(2)矩形的面积为10时,它的宽y和长x之间的关系.
C=4a
是正比例函数
是反比例函数
是正比例函数
是反比例函数
(3)运动会的田径比赛中,运动员小王的平均速度
是8米/秒,他所跑过的路程S和所用时间t之间的
关系.
(4)王师傅要生产100个零件,他的工作效率P和工
作时间t之间的关系.
S=8t
3. 已知反比例函数y= .
(1)说出这个函数的比例系数和自变量的取值范围.
比例系数为-12,自变量的取值范围为x≠0
当x=-3时,y=4
(3)求当y=- 时自变量x的值.
(2)求当x=-3时函数的值.
4. 设面积为10cm2的三角形的一条边长为a(cm),这条边上的高线长为h(cm).
(1)求h关于a的函数表达式和自变量a的取值范围.
(1)h关于a的函数表达 ,自变量a的取值范围是a>0
(2)h是关于a的反比例函数,比例系数是20
(3)当a=2.5cm时,h=8cm
(2)h关于a的函数是不是反比例函数 如果是,请说出它的比例系数.
(3)求当边长a=2.5cm时,这条边上的高线长.
给我一个支点,我可以撬动地球!
——阿基米德
背景知识
阻力臂
阻力
动力臂
动力
背景知识
杠杆定律
【例1】如图,阻力为1000N,阻力臂长为5cm.设动力y(N),动力臂为x(cm)(图中杠杆本身所受重力略去不计。杠杆平衡时:动力×动力臂=阻力×阻力臂)
(1)求y关于x的函数解析式。这个函数是反比例函数吗 如果是,请说出比例系数;
(2)求当x=50时,函数y的值,并说明这个值的实际意义;
(3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n倍时,所需动力将怎样变化?
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
