浙教版七年级上册 1.3 绝对值 课件(共15张PPT)
文档属性
| 名称 | 浙教版七年级上册 1.3 绝对值 课件(共15张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 593.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 19:39:41 | ||
图片预览






文档简介
(共15张PPT)
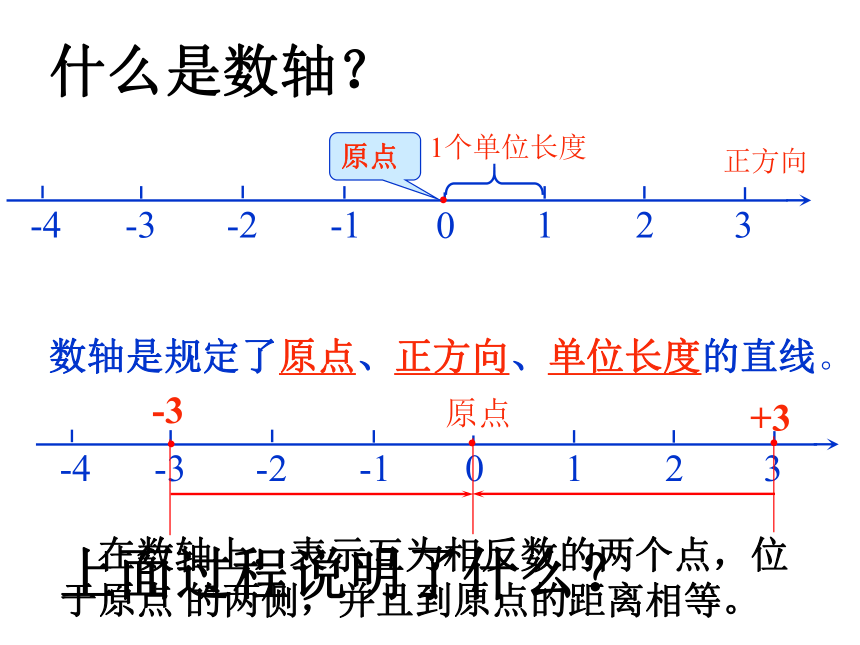
在数轴上,表示互为相反数的两个点,位于原点 的两侧,并且到原点的距离相等。
什么是数轴?
0
-4
-3
-2
-1
3
2
1
1个单位长度
原点
正方向
数轴是规定了原点、正方向、单位长度的直线。
上面过程说明了什么?
0
-4
-3
-2
-1
3
2
1
-3
+3
原点
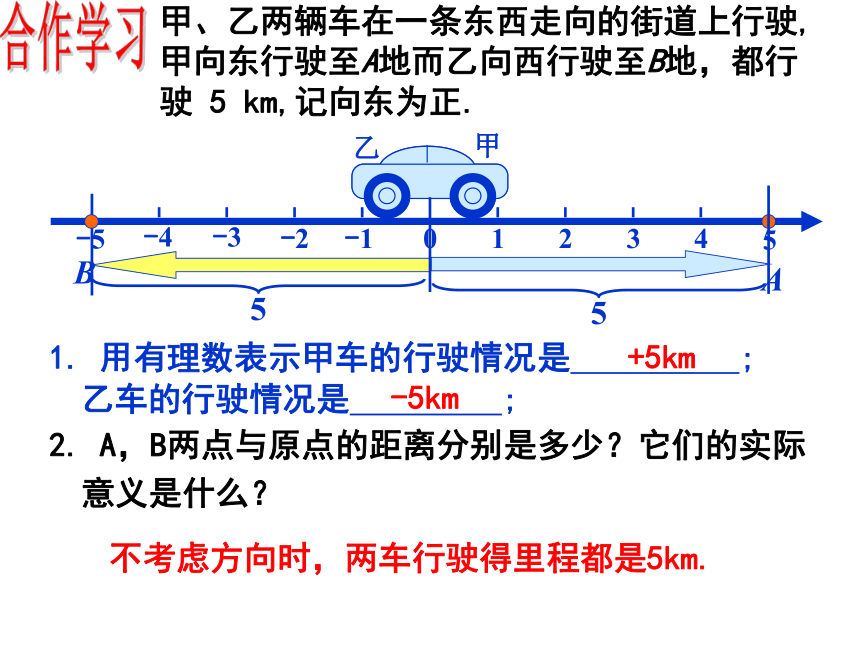
甲、乙两辆车在一条东西走向的街道上行驶,
甲向东行驶至A地而乙向西行驶至B地,都行
驶 5 km,记向东为正.
1. 用有理数表示甲车的行驶情况是 ;
0
1
2
3
4
-1
-2
-3
-4
-5
乙
甲
5
5
5
B
A
2. A,B两点与原点的距离分别是多少?它们的实际意义是什么?
+5km
乙车的行驶情况是 ;
-5km
不考虑方向时,两车行驶得里程都是5km.
数轴上表示-5和5的点到原点的距离分别是多少?
1.3 绝对值
例如,数轴上表示-5的点与原点的距离是5,所以-5的绝对值是5,记做|-5 |=5;5的绝对值也是5,记做|5 |=5
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
|-3 |表示什么意义?
(1) |+0.2 |= ____;
(2) |+2 |=___;
(3) |-2|=___;
0.2
2
(4) |-0.2|=___;
(5) | 0 |=___.
0
2
0.2
正数的绝对值是它本身;
负数的绝对值是它的相反数;
零的绝对值是零.
互为相反数的两个数的绝对值相等.
问题:从上面的结果你能得到哪些结论?
先说说下列绝对值的实际意义再求值
问题:绝对值是本身的数有________
例1 求下列各数的绝对值:
解:
计算:
解:
=4
P16 1 4
P17 2
例2: 求绝对值等于4的数.
解: 方法一: 数轴法
方法二:
∵数轴上到原点距离等于4个单位长度的点有两个.
如图:点P和点Q到原点的距离为4.
∴绝对值等于4的数是+4和-4.
∴绝对值等于4的数是+4和-4.
0
2
4
6
8
-6
-4
-2
P
Q
思考1.绝对值小于4的整数有几个?
思考2.绝对值不大于4的整数有几个?
思考3.绝对值小于4的有理数有几个?
思考4.绝对值大于2.5且小于7.4的整数有哪几个
有7个,分别是0,1,2,3,-1,-2,-3
无数个
例3: 数轴上到4的距离等于5的数是多少
解:
数轴上到4距离等于5的点对应的数有
9和-1.
由作图可知:
●
●
●
1. 一个数的绝对值一定是正数. ( )
2. 一个数的绝对值不可能是负数( )
3. 绝对值是一个正数的数有两个.( )
4. 绝对值是它本身的数是正数. ( )
5. 正数的绝对值是它本身. ( )
6. 负数的绝对值是它的相反数. ( )
7. 绝对值是它的相反数的数是负数( )
注意: 在考虑绝对值时,0是很容易被忽视的.
正数和0
(非负数)
正数和0
(非负数)
负数和0
(非正数)
某企业生产瓶装食用调和油,根据质量要求,净含量(不含包装)可以有0.0021L的误差,现从中抽取6瓶进行检验,超过规定净含量的记做正数,不足规定净含量的记做负数。检查结果如下:
1 2 3 4 5 6
+0.0018 -0.0023 +0.0025 -0.0015 +0.0012 +0.0010
请用绝对值的知识说明:
(1)哪几瓶是符合要求的(即在允许的误差范围内);
(2)哪一瓶的净含量最接近规定的净含量?
绝对值越小,越接近规定的净含量。
一个数在数轴上表示的点离原点的距离越远,绝对值
______;离原点的距离______,绝对值越小。
3、 求a、b的值
任何一个数的绝对值大于等于0!
P17 4 5
1.绝对值的概念:
(1)正数的绝对值是它本身;
(2)负数的绝对值是它的相反数:
(3)0的绝对值是0
(4)互为相反数的两个数的绝对值相等.
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
2.绝对值的性质:
1、求绝对值小于3的整数
2、求绝对值大于 且小于 的整数
在数轴上,表示互为相反数的两个点,位于原点 的两侧,并且到原点的距离相等。
什么是数轴?
0
-4
-3
-2
-1
3
2
1
1个单位长度
原点
正方向
数轴是规定了原点、正方向、单位长度的直线。
上面过程说明了什么?
0
-4
-3
-2
-1
3
2
1
-3
+3
原点
甲、乙两辆车在一条东西走向的街道上行驶,
甲向东行驶至A地而乙向西行驶至B地,都行
驶 5 km,记向东为正.
1. 用有理数表示甲车的行驶情况是 ;
0
1
2
3
4
-1
-2
-3
-4
-5
乙
甲
5
5
5
B
A
2. A,B两点与原点的距离分别是多少?它们的实际意义是什么?
+5km
乙车的行驶情况是 ;
-5km
不考虑方向时,两车行驶得里程都是5km.
数轴上表示-5和5的点到原点的距离分别是多少?
1.3 绝对值
例如,数轴上表示-5的点与原点的距离是5,所以-5的绝对值是5,记做|-5 |=5;5的绝对值也是5,记做|5 |=5
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
|-3 |表示什么意义?
(1) |+0.2 |= ____;
(2) |+2 |=___;
(3) |-2|=___;
0.2
2
(4) |-0.2|=___;
(5) | 0 |=___.
0
2
0.2
正数的绝对值是它本身;
负数的绝对值是它的相反数;
零的绝对值是零.
互为相反数的两个数的绝对值相等.
问题:从上面的结果你能得到哪些结论?
先说说下列绝对值的实际意义再求值
问题:绝对值是本身的数有________
例1 求下列各数的绝对值:
解:
计算:
解:
=4
P16 1 4
P17 2
例2: 求绝对值等于4的数.
解: 方法一: 数轴法
方法二:
∵数轴上到原点距离等于4个单位长度的点有两个.
如图:点P和点Q到原点的距离为4.
∴绝对值等于4的数是+4和-4.
∴绝对值等于4的数是+4和-4.
0
2
4
6
8
-6
-4
-2
P
Q
思考1.绝对值小于4的整数有几个?
思考2.绝对值不大于4的整数有几个?
思考3.绝对值小于4的有理数有几个?
思考4.绝对值大于2.5且小于7.4的整数有哪几个
有7个,分别是0,1,2,3,-1,-2,-3
无数个
例3: 数轴上到4的距离等于5的数是多少
解:
数轴上到4距离等于5的点对应的数有
9和-1.
由作图可知:
●
●
●
1. 一个数的绝对值一定是正数. ( )
2. 一个数的绝对值不可能是负数( )
3. 绝对值是一个正数的数有两个.( )
4. 绝对值是它本身的数是正数. ( )
5. 正数的绝对值是它本身. ( )
6. 负数的绝对值是它的相反数. ( )
7. 绝对值是它的相反数的数是负数( )
注意: 在考虑绝对值时,0是很容易被忽视的.
正数和0
(非负数)
正数和0
(非负数)
负数和0
(非正数)
某企业生产瓶装食用调和油,根据质量要求,净含量(不含包装)可以有0.0021L的误差,现从中抽取6瓶进行检验,超过规定净含量的记做正数,不足规定净含量的记做负数。检查结果如下:
1 2 3 4 5 6
+0.0018 -0.0023 +0.0025 -0.0015 +0.0012 +0.0010
请用绝对值的知识说明:
(1)哪几瓶是符合要求的(即在允许的误差范围内);
(2)哪一瓶的净含量最接近规定的净含量?
绝对值越小,越接近规定的净含量。
一个数在数轴上表示的点离原点的距离越远,绝对值
______;离原点的距离______,绝对值越小。
3、 求a、b的值
任何一个数的绝对值大于等于0!
P17 4 5
1.绝对值的概念:
(1)正数的绝对值是它本身;
(2)负数的绝对值是它的相反数:
(3)0的绝对值是0
(4)互为相反数的两个数的绝对值相等.
一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.
2.绝对值的性质:
1、求绝对值小于3的整数
2、求绝对值大于 且小于 的整数
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
