1.4 二次函数的应用 (2) 课件(共17张PPT)
文档属性
| 名称 | 1.4 二次函数的应用 (2) 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 12:54:13 | ||
图片预览





文档简介
(共17张PPT)
1.4 二次函数的应用(2)
浙教版九年级上册
1.一般形式:
2. 顶点式:
3.交点式:
y=ax +bx+c (a,b,c为常数,a ≠0)
y=a(x - h)2+k (a ≠0)
y=a(x-x1)(x-x2) (a ≠0)
齐声朗读
顶点坐标:(h,k)
二次函数表达式:
新知导入
如何求下列函数的最值?
a=1>0,抛物线开口向上,有最小值,
.
将函数配方化简:
.
当x=-1时,最小值是3,
.
ymin=
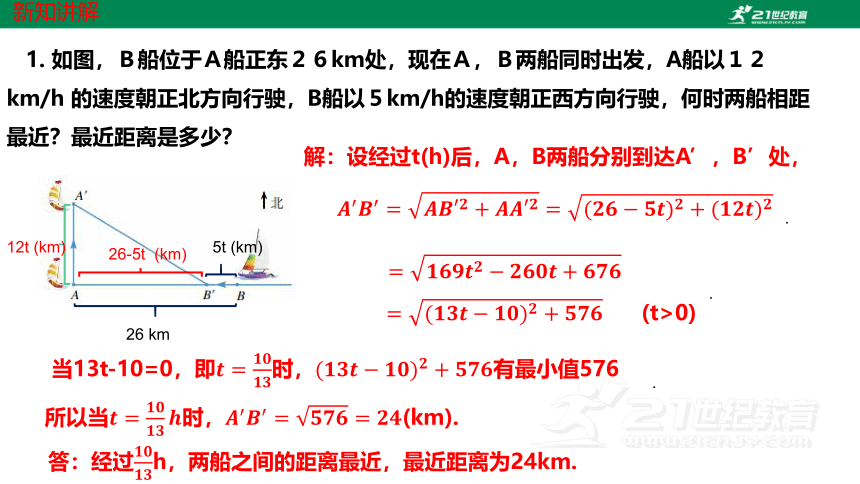
1. 如图,B船位于A船正东26km处,现在A,B两船同时出发,A船以12km/h 的速度朝正北方向行驶,B船以5km/h的速度朝正西方向行驶,何时两船相距最近?最近距离是多少?
所以当时,(km).
答:经过h,两船之间的距离最近,最近距离为24km.
26 km
5t (km)
26-5t (km)
12t (km)
解:设经过t(h)后,A,B两船分别到达A’,B’处,
.
(t>0)
.
当13t-10=0,即时,有最小值576
.
新知讲解
2.某超市销售一种饮料,每瓶进价为9元.经市场调查表明,当售价在10元到14元之间(含10元,14元)浮动时,每瓶售价每增加0.5元,日均销售量减少40瓶;当售价为每瓶12元时,日均销售量为400瓶.问销售价格定为每瓶多少元时,所得日均毛利润(每瓶毛利润=每瓶售价-每瓶进价)最大?最大日均毛利润为多少元?
当x=13时,(元)
答:售价定为每瓶13元时,所得日均毛利润最大,最大日均毛利润为1280元。
每增加1元
减少80瓶
解:设每瓶售价x元,日均毛利润为y元,日均销售量:400-80(x-12)=1360-80x 件
.
得:y=(x-9)(1360-80x)= (10≤x≤14)
.
,在10≤x≤14的范围内.
.
售价基数
“总利润=单件利润×销售量”
日均销售量基数
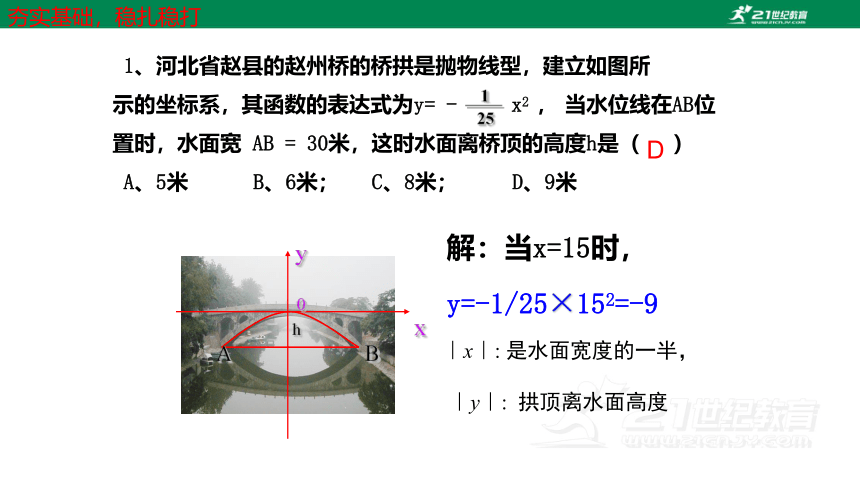
1、河北省赵县的赵州桥的桥拱是抛物线型,建立如图所
示的坐标系,其函数的表达式为y= - x2 , 当水位线在AB位
置时,水面宽 AB = 30米,这时水面离桥顶的高度h是( )
A、5米 B、6米; C、8米; D、9米
1
25
0
x
y
h
A B
解:当x=15时,
y=-1/25×152=-9
夯实基础,稳扎稳打
|x|: 是水面宽度的一半,
|y|: 拱顶离水面高度
D
2.如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
x
0
y
A
解:如图建立坐标系,以抛物线顶点
为原点O,A( 2,-2)、
设抛物线为y=ax2
-2=a2
a
y=x2
B
B( m,-3)
-3=2
水面下降1m,
水面纵坐标为 -3 ,
m=
水面宽度:2
水面宽度增加:
.
3、某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价1元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?
分析:利润=(每件商品所获利润)× (销售件数)
解:设每个涨价x元,共获利润 y元, 那么
(1)销售价可以表示为 ;
(50+x)元
(2)一个商品所获利润可以表示为 ;
(50+x-40)元
(3)销售量可以表示为 ;
(500-10x) 个
(4)共获利润可以表示为 ;
(50+x-40)(500-10x)元
y=(50+x-40)(500-10x)
=(10+x)(500-10x)
=-10x2+400x+5000
=-10(x2-40x+400-400)+5000
=-10(x-20)2+9000
当x=20,每个涨价20元,(元)
4.杂技团进行杂技表演,演员从跷跷板一端弹跳到人梯顶端,其身体(看成一点)的路线(由A到B)是抛物线y= - x2+3x+1的一部分,如图.?
(1)求演员离地面的最大高度;?
(2)已知人梯高BC=3.4m,在一次表演中,人梯到起跳点A的水平距离是4m,则这次表演是否成功?请说明理由.
5.已知x=2t-5,y=10-t,s=xy,求s的最大值或最小值,以及相应t的值
s=xy=(2t-5)(10-t)
=-2t2+25t-50
a=-2,b=25,c=50
t=-
-
S
连续递推,豁然开朗
6.当a≤x≤a+1时,函数y=x2-2x+1的最小值为1,则a的值为( )
A.-1 B.2
C.0或2 D.-1或2
D
x
0
y
x
0
y
x
0
y
a+1=0
a=2
不等式是图像的一部分
7.公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O点恰在水面中心,OA=1.25米,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下.为使水流较为漂亮,要求设计成水流在离OA距离为1米处达到距水面最大高度2.25米.如果不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流落不到池外?
1.25米
解:如图建立坐标系,设抛物线顶点
为B,水流落水与x轴交于C点.
由题意可知A( 0,1.25)、
B( 1,2.25 )、C(x0,0).
设抛物线为y=a(x-1)2+2.25 (a≠0),
点A坐标代入,得a= - 1;
∴抛物线为y=-(x-1)2+2.25.
当y= 0时, x1= - 0.5(舍去), x2=2.5
∴水池的半径至少要2.5米.
A
B
C
O
x
y
8. 如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
解:建立直角坐标系.则点A(1.5,3.05),
B(0,3.5).以点C表示运动员投篮球的出手处.
设抛物线的解析式为 y=a(x-0)2+k ,即y=ax2+k.
所以该抛物线的表达式为y=-0.2x2+3.5.当 x=-2.5时,y=2.25 .故该运动员出手时的高度为2.25m.21*cnjy*com
x
0
y
A
B
C
8. 如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
解:建立直角坐标系.则点A(4,3.05),
B(2.5,3.5).以点C表示运动员投篮球的出手处.
设抛物线的解析式为 y=a(x-2.5)2+3.5 ,
y=-0.2(x-2.5)2+3.5 =-0.2x2+x+2.25.
当 x=0时,y=2.25 .
故该运动员出手时的高度为2.25m.21*cnjy*com
x
0
y
A
B
C
3.05=a(4-2.5)2+3.5
2.25a=-0.45
a=-0.2
9、有一种大棚种植的西红柿,经过实验,其单位面积的产量与这个单位面积种植的株数成构成一种函数关系。每平方米种植4株时,平均单株产量为2kg;以同样的栽培条件,每平方米种植的株数每增加1株,单株产量减少1/4kg。
问每平方米种植多少株时,能获得最大的产量?最大的产量为多少?
法1:解:设每平方米种植x株,产量为y (kg)
法2:每平方米种植的株数增加x株,
y=x(2 -
.
=x(3 -
= -
= -
= -
= -
当x=6时,(kg)
y=(x+4)(2 -
.
.
= -
= -
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.4 二次函数的应用(2)
浙教版九年级上册
1.一般形式:
2. 顶点式:
3.交点式:
y=ax +bx+c (a,b,c为常数,a ≠0)
y=a(x - h)2+k (a ≠0)
y=a(x-x1)(x-x2) (a ≠0)
齐声朗读
顶点坐标:(h,k)
二次函数表达式:
新知导入
如何求下列函数的最值?
a=1>0,抛物线开口向上,有最小值,
.
将函数配方化简:
.
当x=-1时,最小值是3,
.
ymin=
1. 如图,B船位于A船正东26km处,现在A,B两船同时出发,A船以12km/h 的速度朝正北方向行驶,B船以5km/h的速度朝正西方向行驶,何时两船相距最近?最近距离是多少?
所以当时,(km).
答:经过h,两船之间的距离最近,最近距离为24km.
26 km
5t (km)
26-5t (km)
12t (km)
解:设经过t(h)后,A,B两船分别到达A’,B’处,
.
(t>0)
.
当13t-10=0,即时,有最小值576
.
新知讲解
2.某超市销售一种饮料,每瓶进价为9元.经市场调查表明,当售价在10元到14元之间(含10元,14元)浮动时,每瓶售价每增加0.5元,日均销售量减少40瓶;当售价为每瓶12元时,日均销售量为400瓶.问销售价格定为每瓶多少元时,所得日均毛利润(每瓶毛利润=每瓶售价-每瓶进价)最大?最大日均毛利润为多少元?
当x=13时,(元)
答:售价定为每瓶13元时,所得日均毛利润最大,最大日均毛利润为1280元。
每增加1元
减少80瓶
解:设每瓶售价x元,日均毛利润为y元,日均销售量:400-80(x-12)=1360-80x 件
.
得:y=(x-9)(1360-80x)= (10≤x≤14)
.
,在10≤x≤14的范围内.
.
售价基数
“总利润=单件利润×销售量”
日均销售量基数
1、河北省赵县的赵州桥的桥拱是抛物线型,建立如图所
示的坐标系,其函数的表达式为y= - x2 , 当水位线在AB位
置时,水面宽 AB = 30米,这时水面离桥顶的高度h是( )
A、5米 B、6米; C、8米; D、9米
1
25
0
x
y
h
A B
解:当x=15时,
y=-1/25×152=-9
夯实基础,稳扎稳打
|x|: 是水面宽度的一半,
|y|: 拱顶离水面高度
D
2.如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
x
0
y
A
解:如图建立坐标系,以抛物线顶点
为原点O,A( 2,-2)、
设抛物线为y=ax2
-2=a2
a
y=x2
B
B( m,-3)
-3=2
水面下降1m,
水面纵坐标为 -3 ,
m=
水面宽度:2
水面宽度增加:
.
3、某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价1元,销量减少10个,为赚得最大利润,售价定为多少?最大利润是多少?
分析:利润=(每件商品所获利润)× (销售件数)
解:设每个涨价x元,共获利润 y元, 那么
(1)销售价可以表示为 ;
(50+x)元
(2)一个商品所获利润可以表示为 ;
(50+x-40)元
(3)销售量可以表示为 ;
(500-10x) 个
(4)共获利润可以表示为 ;
(50+x-40)(500-10x)元
y=(50+x-40)(500-10x)
=(10+x)(500-10x)
=-10x2+400x+5000
=-10(x2-40x+400-400)+5000
=-10(x-20)2+9000
当x=20,每个涨价20元,(元)
4.杂技团进行杂技表演,演员从跷跷板一端弹跳到人梯顶端,其身体(看成一点)的路线(由A到B)是抛物线y= - x2+3x+1的一部分,如图.?
(1)求演员离地面的最大高度;?
(2)已知人梯高BC=3.4m,在一次表演中,人梯到起跳点A的水平距离是4m,则这次表演是否成功?请说明理由.
5.已知x=2t-5,y=10-t,s=xy,求s的最大值或最小值,以及相应t的值
s=xy=(2t-5)(10-t)
=-2t2+25t-50
a=-2,b=25,c=50
t=-
-
S
连续递推,豁然开朗
6.当a≤x≤a+1时,函数y=x2-2x+1的最小值为1,则a的值为( )
A.-1 B.2
C.0或2 D.-1或2
D
x
0
y
x
0
y
x
0
y
a+1=0
a=2
不等式是图像的一部分
7.公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O点恰在水面中心,OA=1.25米,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下.为使水流较为漂亮,要求设计成水流在离OA距离为1米处达到距水面最大高度2.25米.如果不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流落不到池外?
1.25米
解:如图建立坐标系,设抛物线顶点
为B,水流落水与x轴交于C点.
由题意可知A( 0,1.25)、
B( 1,2.25 )、C(x0,0).
设抛物线为y=a(x-1)2+2.25 (a≠0),
点A坐标代入,得a= - 1;
∴抛物线为y=-(x-1)2+2.25.
当y= 0时, x1= - 0.5(舍去), x2=2.5
∴水池的半径至少要2.5米.
A
B
C
O
x
y
8. 如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
解:建立直角坐标系.则点A(1.5,3.05),
B(0,3.5).以点C表示运动员投篮球的出手处.
设抛物线的解析式为 y=a(x-0)2+k ,即y=ax2+k.
所以该抛物线的表达式为y=-0.2x2+3.5.当 x=-2.5时,y=2.25 .故该运动员出手时的高度为2.25m.21*cnjy*com
x
0
y
A
B
C
8. 如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
解:建立直角坐标系.则点A(4,3.05),
B(2.5,3.5).以点C表示运动员投篮球的出手处.
设抛物线的解析式为 y=a(x-2.5)2+3.5 ,
y=-0.2(x-2.5)2+3.5 =-0.2x2+x+2.25.
当 x=0时,y=2.25 .
故该运动员出手时的高度为2.25m.21*cnjy*com
x
0
y
A
B
C
3.05=a(4-2.5)2+3.5
2.25a=-0.45
a=-0.2
9、有一种大棚种植的西红柿,经过实验,其单位面积的产量与这个单位面积种植的株数成构成一种函数关系。每平方米种植4株时,平均单株产量为2kg;以同样的栽培条件,每平方米种植的株数每增加1株,单株产量减少1/4kg。
问每平方米种植多少株时,能获得最大的产量?最大的产量为多少?
法1:解:设每平方米种植x株,产量为y (kg)
法2:每平方米种植的株数增加x株,
y=x(2 -
.
=x(3 -
= -
= -
= -
= -
当x=6时,(kg)
y=(x+4)(2 -
.
.
= -
= -
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
