第一章 二次函数 章末复习----三个“二” 课件(共17张PPT)
文档属性
| 名称 | 第一章 二次函数 章末复习----三个“二” 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-26 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
第一章 二次函数 章末复习
--------三个“二”
浙教版九年级上册
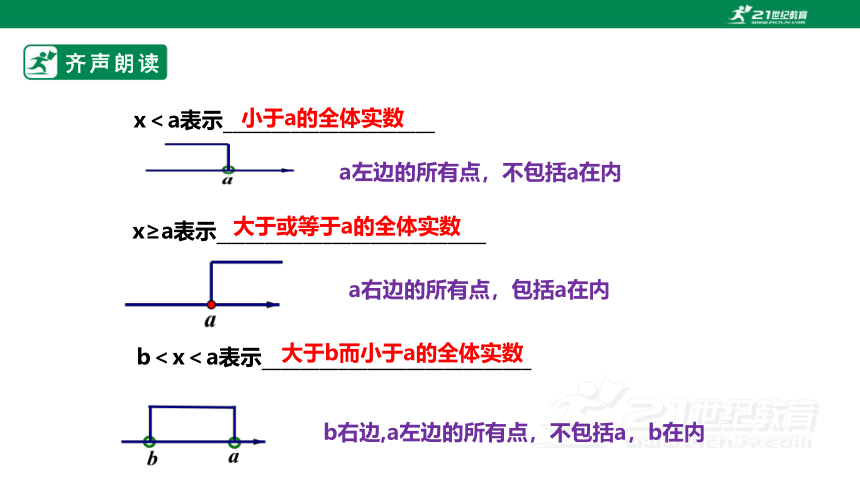
x<a表示______________________
小于a的全体实数
x≥a表示____________________________
大于或等于a的全体实数
a右边的所有点,包括a在内
a左边的所有点,不包括a在内
b<x<a表示____________________________
大于b而小于a的全体实数
b右边,a左边的所有点,不包括a,b在内
齐声朗读
1
2
0
3
4
-1
-2
-3
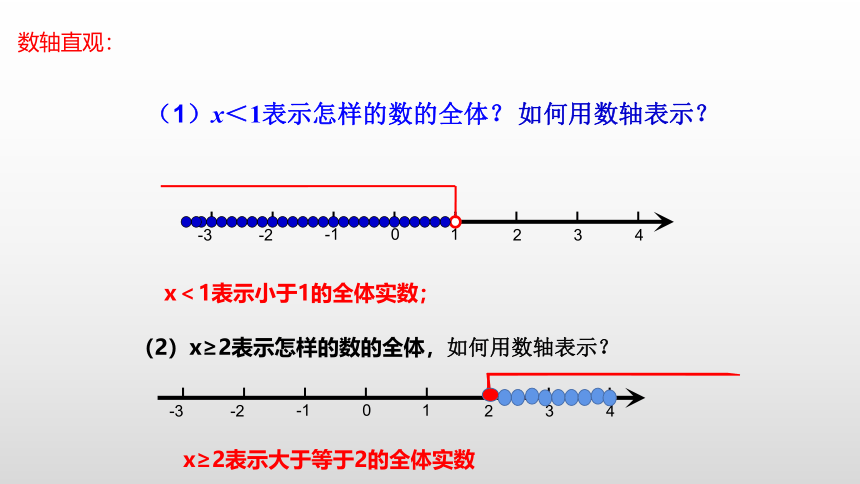
(1)x<1表示怎样的数的全体?
如何用数轴表示?
1
2
0
3
4
-1
-2
-3
(2)x≥2表示怎样的数的全体,如何用数轴表示?
x<1表示小于1的全体实数;
x≥2表示大于等于2的全体实数
数轴直观:
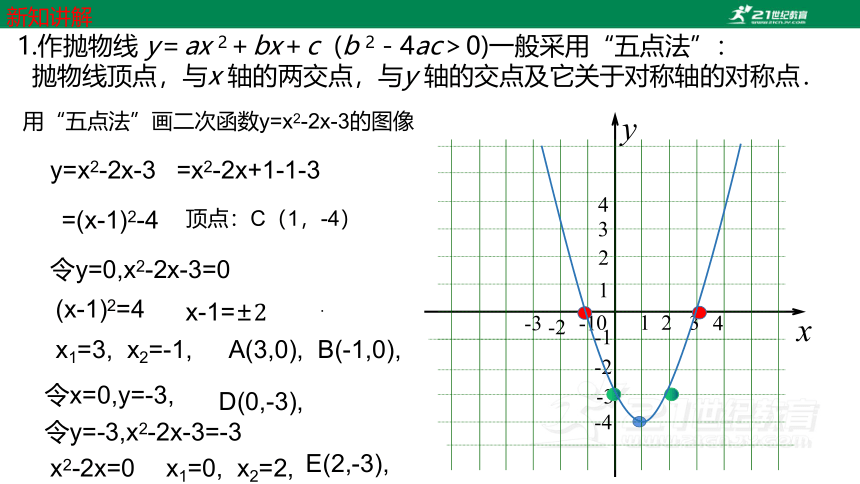
1.作抛物线 y=ax 2+bx+c (b 2-4ac>0)一般采用“五点法”:
抛物线顶点,与x 轴的两交点,与y 轴的交点及它关于对称轴的对称点.
y=x2-2x-3
=x2-2x+1-1-3
=(x-1)2-4
顶点:C(1,-4)
令y=0,x2-2x-3=0
(x-1)2=4
x1=3, x2=-1,
A(3,0), B(-1,0),
令x=0,y=-3,
D(0,-3),
令y=-3,x2-2x-3=-3
x2-2x=0
x1=0, x2=2,
E(2,-3),
用“五点法”画二次函数y=x2-2x-3的图像
x
y
0
1
2
3
4
-1
-2
-3
1
2
3
4
-1
-2
-3
-4
x-1=
.
新知讲解
y=x2-2x-3
x
y
0
1
2
3
4
-1
-2
-3
1
2
3
4
-1
-2
-3
-4
(2)根据二次函数值的取值范围确定自变量的取值范围,一般要画出二次函数的图象,观察图象解答,抛物线在x 轴上方的部分,对应的函数值大于0;抛物线在x 轴下方的部分,对应的函数值小于0;抛物线与x 轴的公共点,对应的函数值等于0.
y=x2-2x-3
方程x2-2x-3=0是函数y=x2-2x-3的0点位置
函数值为0
0点位置
从函数视角看,x2-2x-3>0是什么?
函数值>0
在x 轴上方的部分
不等式x2-2x-3>0是抛物线y=x2-2x-3
在x 轴上方的部分
解不等式:x2-2x-3>0
x<-1或x>3
y=x2-2x-3
x
y
0
1
2
3
4
-1
-2
-3
1
2
3
4
-1
-2
-3
-4
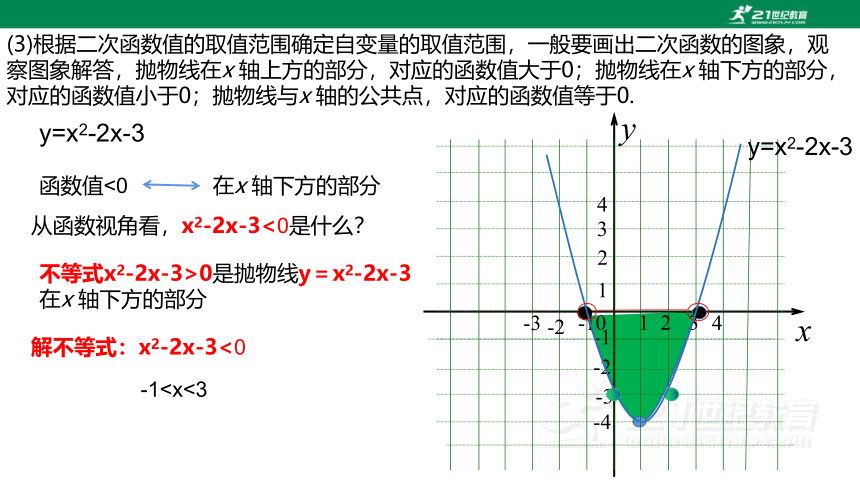
(3)根据二次函数值的取值范围确定自变量的取值范围,一般要画出二次函数的图象,观察图象解答,抛物线在x 轴上方的部分,对应的函数值大于0;抛物线在x 轴下方的部分,对应的函数值小于0;抛物线与x 轴的公共点,对应的函数值等于0.
y=x2-2x-3
函数值<0
在x 轴下方的部分
从函数视角看,x2-2x-3<0是什么?
不等式x2-2x-3>0是抛物线y=x2-2x-3
在x 轴下方的部分
解不等式:x2-2x-3<0
-1x
y
0
1
2
3
4
-1
-2
-3
1
2
3
4
-1
-2
-3
-4
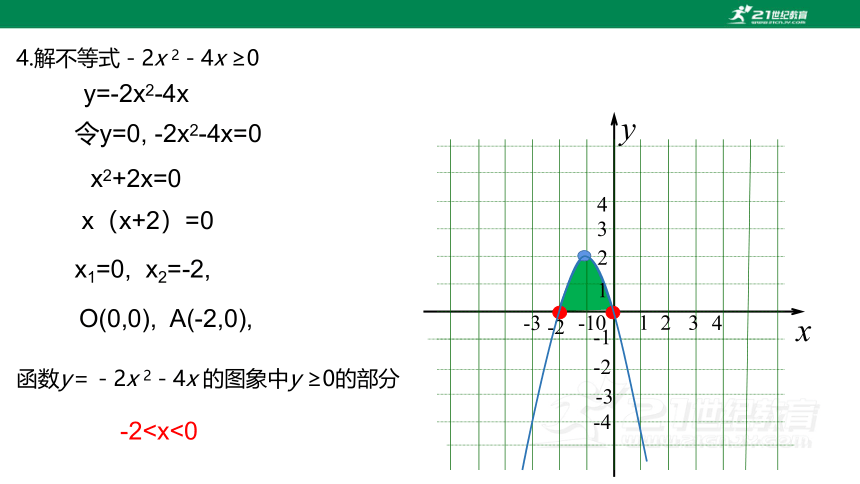
4.解不等式-2x 2-4x ≥0
y=-2x2-4x
令y=0, -2x2-4x=0
x2+2x=0
x(x+2)=0
x1=0, x2=-2,
O(0,0), A(-2,0),
函数y=-2x 2-4x 的图象中y ≥0的部分
-2知识
利用二次函数的图象解一元二次不等式
图象 函数值 自变量的取值(范围)
y>0
x<x1或x>x2
y=0
x=x1或x=x2
y<0
x1<x<x2
y>0
x1<x<x2
y=0
x=x1或x=x2
y<0
x<x1或x>x2
方程是函数的特殊位置,
不等式是函数的一部分
1.抛物线y=ax2+bx+c(a<0)的图象如图所示,则关于x的不等式ax2+bx+c>0的解集是( )
A.x<2 B.x>-3
C.-31
C
夯实基础,稳扎稳打
2.如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),B(2,0).
(1)方程ax2+bx+c=0的解为________________;
(2)不等式ax2+bx+c>0的解集为____________;
(3)不等式ax2+bx+c≤0的解集为____________.
x1=-1,x2=2
-1<x<2
x≤-1或x≥2
相交
3.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
解:x1=1,x2=3.
1<x<3.
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
解:x>2.
解∵方程ax 2+bx+c=k 有两个不相等的实数根,
∴抛物线 y=ax 2+bx+c 与直线y=k 有两个交点.∴k<2.
水平线y=k
水平线y=k
切线y=2
连续递推,豁然开朗
相交
相切
相离
4.如图,抛物线y=ax2+c与直线y=mx+n交于A(-1,p),B(3,q)两点,则不等式ax2 - mx+c>n的解集
是________________.
x<-3或x>1
ax2 - mx+c>n
ax2 +c>mx+n
抛物线y=ax2+c在直线y=mx+n上方
移项处理
5.如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
A.b2>4ac B.ax2+bx+c≥-6
C.若点(-2,m),(-5,n)在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1
C
6.[二次函数与绝对值方程]二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是 ( )
A.k<-3 B.k>-3 C.k<3 D.k>3
当ax2+bx+c≥0时,y=|ax2+bx+c|=ax2+bx+c,此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c(a≠0)在x轴上方部分的图象(包括与x轴的交点);当ax2+bx+c<0时,
y=|ax2+bx+c|=-(ax2+bx+c),此时y=|ax2+bx+c|的图象是函数 y=ax2+bx+c(a≠0)在x轴下方部分与x轴对称的图象.所以y=|ax2+bx+c|的图象如图所示.观察图象可得,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k>3.
切线y=3
D
常数函数: y=k(k是常数)
绝对值函数:y=|ax2+bx+c|
图像有交点,联立解析式
思维拓展,更上一层
7.[直线与双抛物线的交点问题]如图,抛物线y=-2(x-2)2+2与x轴交于点A,B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是 .
3.-3.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第一章 二次函数 章末复习
--------三个“二”
浙教版九年级上册
x<a表示______________________
小于a的全体实数
x≥a表示____________________________
大于或等于a的全体实数
a右边的所有点,包括a在内
a左边的所有点,不包括a在内
b<x<a表示____________________________
大于b而小于a的全体实数
b右边,a左边的所有点,不包括a,b在内
齐声朗读
1
2
0
3
4
-1
-2
-3
(1)x<1表示怎样的数的全体?
如何用数轴表示?
1
2
0
3
4
-1
-2
-3
(2)x≥2表示怎样的数的全体,如何用数轴表示?
x<1表示小于1的全体实数;
x≥2表示大于等于2的全体实数
数轴直观:
1.作抛物线 y=ax 2+bx+c (b 2-4ac>0)一般采用“五点法”:
抛物线顶点,与x 轴的两交点,与y 轴的交点及它关于对称轴的对称点.
y=x2-2x-3
=x2-2x+1-1-3
=(x-1)2-4
顶点:C(1,-4)
令y=0,x2-2x-3=0
(x-1)2=4
x1=3, x2=-1,
A(3,0), B(-1,0),
令x=0,y=-3,
D(0,-3),
令y=-3,x2-2x-3=-3
x2-2x=0
x1=0, x2=2,
E(2,-3),
用“五点法”画二次函数y=x2-2x-3的图像
x
y
0
1
2
3
4
-1
-2
-3
1
2
3
4
-1
-2
-3
-4
x-1=
.
新知讲解
y=x2-2x-3
x
y
0
1
2
3
4
-1
-2
-3
1
2
3
4
-1
-2
-3
-4
(2)根据二次函数值的取值范围确定自变量的取值范围,一般要画出二次函数的图象,观察图象解答,抛物线在x 轴上方的部分,对应的函数值大于0;抛物线在x 轴下方的部分,对应的函数值小于0;抛物线与x 轴的公共点,对应的函数值等于0.
y=x2-2x-3
方程x2-2x-3=0是函数y=x2-2x-3的0点位置
函数值为0
0点位置
从函数视角看,x2-2x-3>0是什么?
函数值>0
在x 轴上方的部分
不等式x2-2x-3>0是抛物线y=x2-2x-3
在x 轴上方的部分
解不等式:x2-2x-3>0
x<-1或x>3
y=x2-2x-3
x
y
0
1
2
3
4
-1
-2
-3
1
2
3
4
-1
-2
-3
-4
(3)根据二次函数值的取值范围确定自变量的取值范围,一般要画出二次函数的图象,观察图象解答,抛物线在x 轴上方的部分,对应的函数值大于0;抛物线在x 轴下方的部分,对应的函数值小于0;抛物线与x 轴的公共点,对应的函数值等于0.
y=x2-2x-3
函数值<0
在x 轴下方的部分
从函数视角看,x2-2x-3<0是什么?
不等式x2-2x-3>0是抛物线y=x2-2x-3
在x 轴下方的部分
解不等式:x2-2x-3<0
-1
y
0
1
2
3
4
-1
-2
-3
1
2
3
4
-1
-2
-3
-4
4.解不等式-2x 2-4x ≥0
y=-2x2-4x
令y=0, -2x2-4x=0
x2+2x=0
x(x+2)=0
x1=0, x2=-2,
O(0,0), A(-2,0),
函数y=-2x 2-4x 的图象中y ≥0的部分
-2
利用二次函数的图象解一元二次不等式
图象 函数值 自变量的取值(范围)
y>0
x<x1或x>x2
y=0
x=x1或x=x2
y<0
x1<x<x2
y>0
x1<x<x2
y=0
x=x1或x=x2
y<0
x<x1或x>x2
方程是函数的特殊位置,
不等式是函数的一部分
1.抛物线y=ax2+bx+c(a<0)的图象如图所示,则关于x的不等式ax2+bx+c>0的解集是( )
A.x<2 B.x>-3
C.-3
C
夯实基础,稳扎稳打
2.如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),B(2,0).
(1)方程ax2+bx+c=0的解为________________;
(2)不等式ax2+bx+c>0的解集为____________;
(3)不等式ax2+bx+c≤0的解集为____________.
x1=-1,x2=2
-1<x<2
x≤-1或x≥2
相交
3.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
解:x1=1,x2=3.
1<x<3.
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
解:x>2.
解∵方程ax 2+bx+c=k 有两个不相等的实数根,
∴抛物线 y=ax 2+bx+c 与直线y=k 有两个交点.∴k<2.
水平线y=k
水平线y=k
切线y=2
连续递推,豁然开朗
相交
相切
相离
4.如图,抛物线y=ax2+c与直线y=mx+n交于A(-1,p),B(3,q)两点,则不等式ax2 - mx+c>n的解集
是________________.
x<-3或x>1
ax2 - mx+c>n
ax2 +c>mx+n
抛物线y=ax2+c在直线y=mx+n上方
移项处理
5.如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
A.b2>4ac B.ax2+bx+c≥-6
C.若点(-2,m),(-5,n)在抛物线上,则m>n
D.关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1
C
6.[二次函数与绝对值方程]二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k的取值范围是 ( )
A.k<-3 B.k>-3 C.k<3 D.k>3
当ax2+bx+c≥0时,y=|ax2+bx+c|=ax2+bx+c,此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c(a≠0)在x轴上方部分的图象(包括与x轴的交点);当ax2+bx+c<0时,
y=|ax2+bx+c|=-(ax2+bx+c),此时y=|ax2+bx+c|的图象是函数 y=ax2+bx+c(a≠0)在x轴下方部分与x轴对称的图象.所以y=|ax2+bx+c|的图象如图所示.观察图象可得,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k>3.
切线y=3
D
常数函数: y=k(k是常数)
绝对值函数:y=|ax2+bx+c|
图像有交点,联立解析式
思维拓展,更上一层
7.[直线与双抛物线的交点问题]如图,抛物线y=-2(x-2)2+2与x轴交于点A,B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是 .
3.-3
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
