全等三角形与三角形全等的判定条件(4课时)
文档属性
| 名称 | 全等三角形与三角形全等的判定条件(4课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-08-21 00:00:00 | ||
图片预览


文档简介
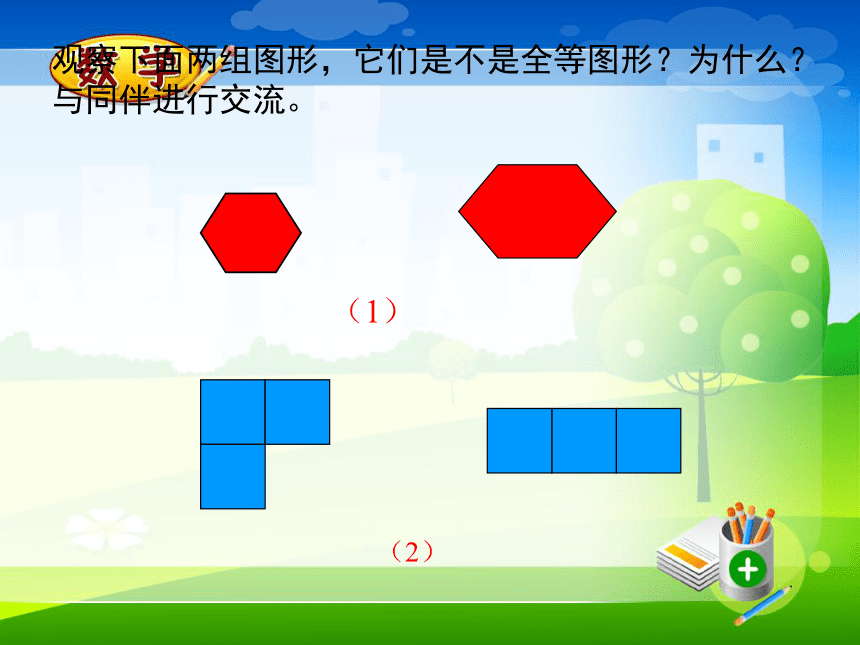
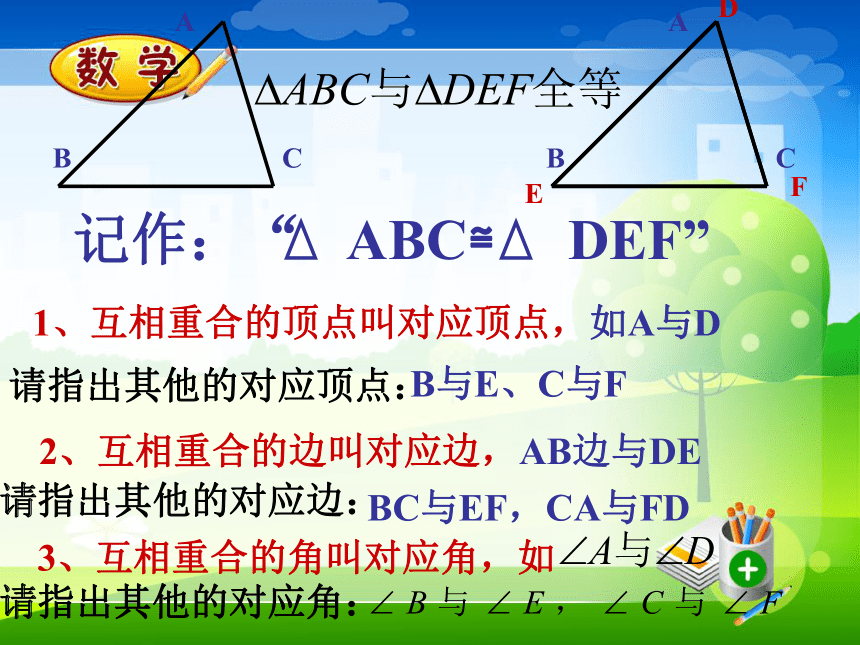
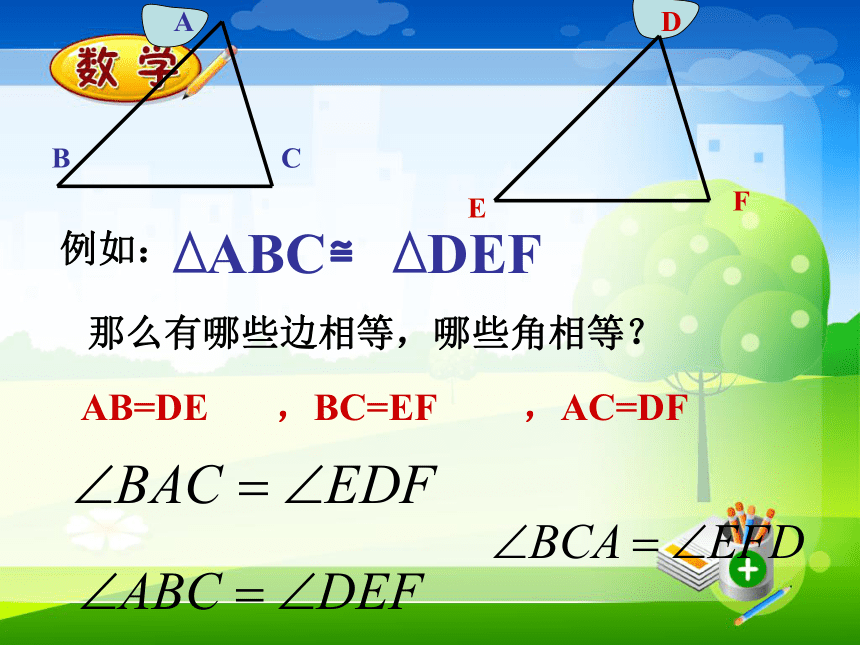
课件99张PPT。1.4全等三角形能够完全重合的两个图形叫做全等形下列同一类的图形有什么特点?观察下面两组图形,它们是不是全等图形?为什么?与同伴进行交流。(1)(2)1、互相重合的顶点叫对应顶点,如A与D请指出其他的对应顶点:B与E、C与F2、互相重合的边叫对应边,AB边与DE请指出其他的对应边:BC与EF,CA与FD3、互相重合的角叫对应角,如请指出其他的对应角: 拿出两个全等的三角形,摆一摆它们的位置,使其符合下列图形;并指出它们的对应顶点、对应边、对应角。注意:全等三角形对应角所对的边是对应边,
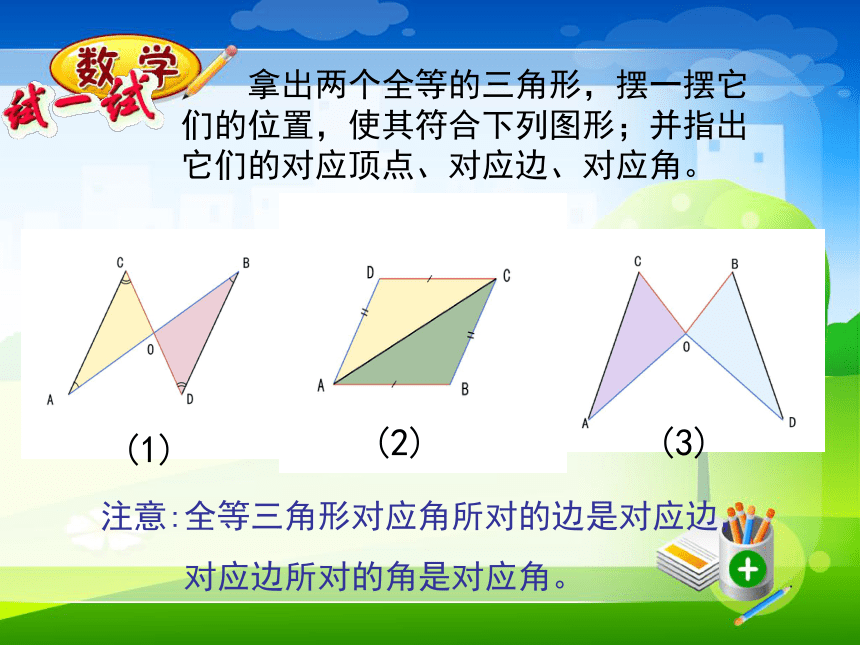
对应边所对的角是对应角。
(1)
(2)
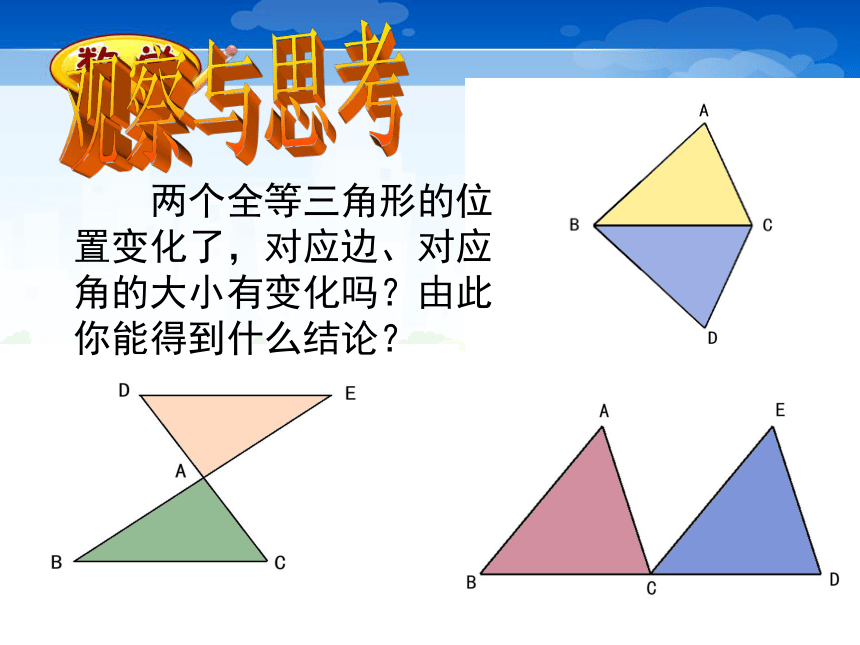
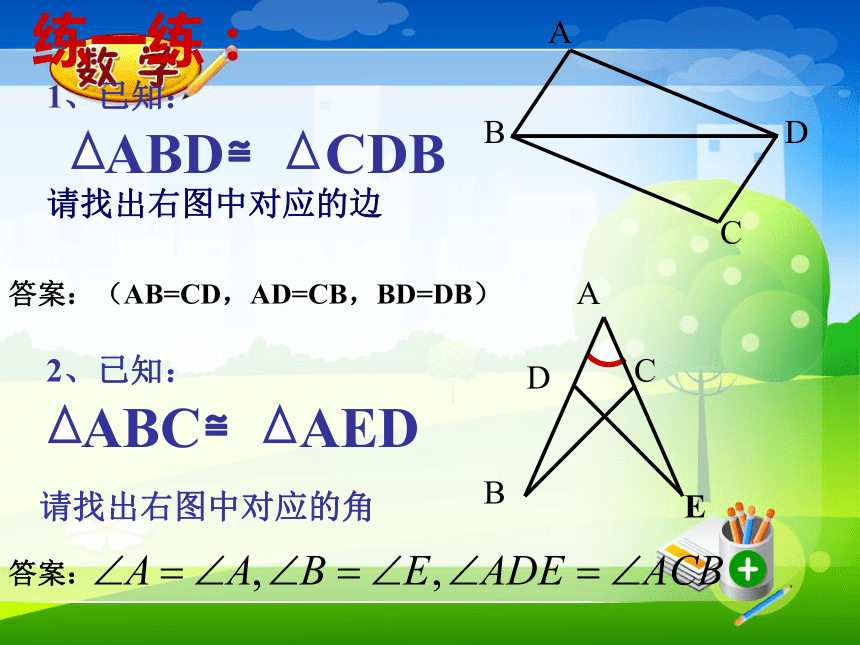
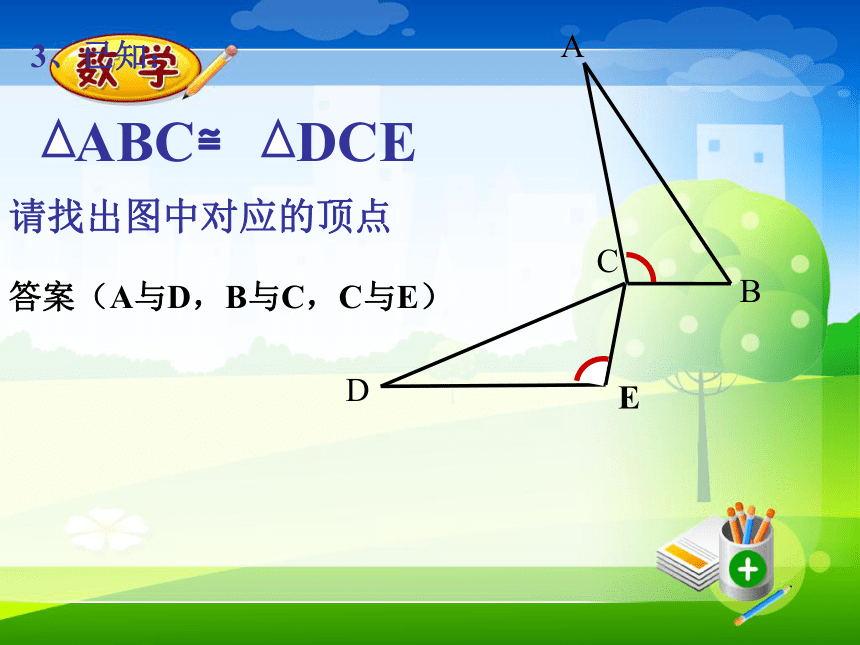
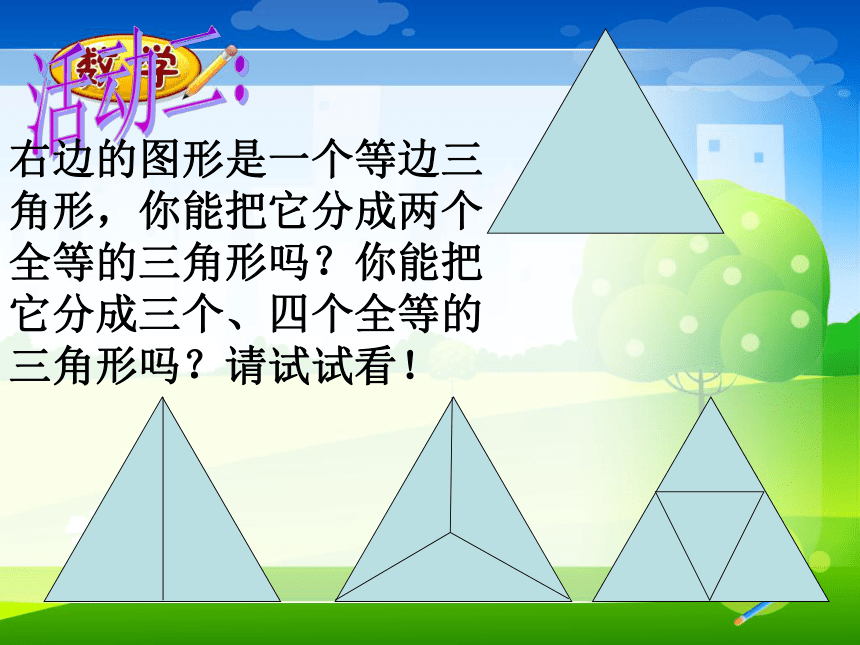
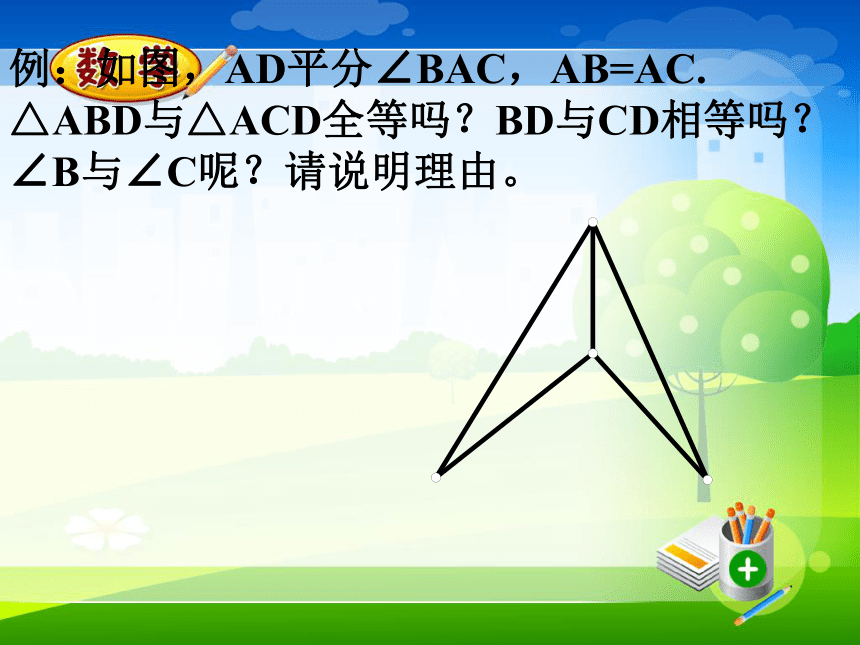
(3) 两个全等三角形的位置变化了,对应边、对应角的大小有变化吗?由此你能得到什么结论?观察与思考那么有哪些边相等,哪些角相等? AB=DE ,BC=EF ,AC=DF答案:(AB=CD,AD=CB,BD=DB)答案:答案(A与D,B与C,C与E)活动二:右边的图形是一个等边三角形,你能把它分成两个全等的三角形吗?你能把它分成三个、四个全等的三角形吗?请试试看!例:如图,AD平分∠BAC,AB=AC.
△ABD与△ACD全等吗?BD与CD相等吗?
∠B与∠C呢?请说明理由。 本节课你学到了哪些知识?
你知道全等三角形有哪些性质吗?
你还想了解关于全等三角形的哪些知识?谈收获1.5 三角形全等的条件(一)知识回顾①AB=DE ② BC=EF ③ CA=FD ④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F2、 什么叫全等三角形?能够重合的两个三角形叫 全等三角形。3、 全等三角形有什么性质?1、什么叫全等图形?能够完全重合的两个图形叫做全等图形。全等三角形对应边相等,对应角相等。1、已知△ADF≌△CBE,则结论:①AF=CE ②∠1=∠2 ③BE=CF ④AE=CF,正确的个数是( )(A)1个(B)2个( C)3个(D)4个课前练习:C2、面积相等的两个三角形一定全等吗?课前练习:3、周长相等的两个三角形一定全等吗?课前练习:试问怎样的三角形才会全等呢?合作学习 1、已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?(不一定全等) 2、已知一个三角形的三条边分别为4cm,5cm,7cm,你能画出这个三角形吗?合作学习画法:1、画线段AB=4cm;2、分别以A、B为圆心,5cm和7cm长为半径画两条圆弧,交于点C;3、连结AC、BC;△ABC就是所求的三角形。 把你画的三角形与同伴画的进行比较,它们一定全等吗? 已知三角形三条边分别是4cm,5cm,7cm,画出这个三角形AB=EFBC=FGAC=EG(SSS)有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)在△ABC和△EFG中用 数学语言表述: 用这样的结论可以判定两个三角形全等. 判断两个三角形全等的推理过程,叫做证明三角形全等. 由上面的结论可知,只要三角形三边长度确定了,这个三角形的形状和大小就完全确定了,三角形的这个性质叫做三角形的稳定性。三角形的稳定性:做一做 有一些长度适当的木条,用钉子把它们分别钉成三角形和四边形,并拉动它们。 三角形的大小和形状是固定不变的,而四边形
的形状会改变。 只要三角形三边的长度确定了,这个三角形的形
状和大小就确定,三角形的这个性质叫三角形的稳定性。 三角形的稳定性举例例1、如图,在四边形ABCD中,AB=CD,AD=CB,则∠A= ∠C,请说明理由。解:在△ABD和△CDB中,(已知)(已知)AB=CDAD=CBBD=DB(公共边)∴ △ABD ≌ △CDB(SSS)∴ ∠A= ∠C(根据什么?)证明:在△ABD和△ACD中,AB=AC(已知)
AD=AD(公共边)
DB=DC (已知)∴ △ ABD≌ △ACD(SSS) 如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架,请说明△ ABD≌ △ ACD的理由。牛刀小试分析:要证明△ ABD≌ △ ACD,首先看这两个三角形的三条边是否对应相等。牛刀小试 如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架,请说明△ ABD≌ △ ACD的理由。小结:从以上的解法中可以看出,说理要由题设(已知)出发,经过一步步的推理,最后推出正确的结论。∠1和∠2相等么?理由呢?能判断直线AD与直线BC的位置关系么?对于本题,你还能得到什么结论?例2、 已知∠BAC,用直尺和圆规∠BAC的角平分线AD,并说明正确的理由。以上是角平分线的尺规画法作法:
1、以点A为圆心,适当的长为半径,与角的两边分别交于E、F两点。3、过点A、D作射线AD。射线AD为所求的平分线。请同学们说说理由练一练: 已知∠α,用直尺和圆规作∠ α的平分线(只要求作出图形,并保留作图痕迹)α例3,如图,已知AB=CD,AD=CB,请说明∠B=∠D解:连结AC,AB=CD(已知)AC=AC(公共边)BC=AD(已知)∴ △ ABC≌ △ CDA(SSS)∴ ∠B=∠D(全等三角形对应角相等)问:此题添加辅助线,若连结BD行吗?在原有条件下,还能推出什么结论?在△ABC和△ ADC中小结:四边形问题转化为三角形问题解决。1、 如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 巩固练习:答: △ABC≌△DCB
理由如下:∵ 在△ABC和△DCB中AB = DCAC = DB=BCCB∴ △ABC≌△DCB(SSS)(公共边)(已知)(已知)2、如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?HDCBA解:有三组。 在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);在△ABH和△ACH中 ∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中 ∵BD=CD,BH=CH,DH=DH∴△DBH≌△DCH(SSS) 3、已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”说明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?解:要说明△ABC ≌△ FDE,还应该有AB=DF这个条件∵ DB是AB与DF的公共部分, 且AD=BF
∴ AD+DB=BF+DB
即 AB=DF4、 如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF。试说明∠A=∠D的理由。解:∵BE=CF(已知)即 BC=EF在△ABC和△DEF中AB=DE(已知)AC=BF(已知)BC=EF(已证)∴△ABC≌△DEF(SSS)∴∠A=∠D(全等三角形对应角相等)小结:欲想说明角相等,先转化为说明三角形全等。∴ BE+EC=CF+EC2. 如图, 在△ABC中,AB=AC, AD是BC边上的中线,则AD⊥BC. ABCD解:∵AD是BC边上的中线∴BD=CD在△ABD和△ACD中AB=AC ( )BD=CD ( )AD=AD ( )已知已证公共边∴△ABD≌△ACD ( )SSS∴∠ADB=∠ADC ( )全等三角形的对应角相等∵∠ADB+∠ADC=180°∴∠ADB=90°,∴AD⊥BC 5、 如图,AB=AC,AE=AD,BD=CE,请说明△AEB ≌ △ ADC的理由。解:∵BD=CE
∴ BD-ED=CE-ED,
即BE=CD。在AEB和ADC中,
AB=AC
AE=AD
BE=CD
∴ △AEB ≌ △ ADC(SSS)(已知)(已知)(已证)请同学们谈谈本节课的收获与体会本节课你学到了什么?
发现了什么?
有什么收获?
还存在什么没有解决的问题? 再 见!要判定两个三角形全等我们已经学过几种方法:1.能完全重合的两个三角形是全等三角形2.有三条边对应相等的两个三角形全等(简称SSS)要判定两个三角形全等还有其它方法吗?1.5 三角形全等的条件(2)创设情景 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。怎样测出A、B两杆之间的距离呢?。AB知识回顾 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。探究1对于三个角对应相等的两个三角形全等吗?如图, △ABC和△ADE中,如果 DE∥AB,则∠A=∠A,∠B=∠ADE,∠C= ∠ AED,但△ABC和△ADE不重合,所以不全等。三个角对应相等的两个三角形不一定全等做一做: 有一个△ABC,它的两边边长分别为3cm、4cm,任意再画一个三角形, 使AB=3cm,AC=4cm。这样画出来的两个三角形进行比较,
它们互相重合吗?画法:2. 在射线AM上截取AB= 3cm3. 在射线AN上截取AC=4cm 若再加一个条件,使∠A=45°,画出△ABC1. 画∠MAN= 45°4.连接BC∴△ABC就是所求的三角形把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?探究2画一画,比一比:让我们动手做一做:用量角器和刻度尺画ΔABC,
使 AB=4cm,BC=6cm,∠ABC=60° 将你画出的三角形和其他同学画的三角形进行比较,它们互相重合吗?由此,你得到了什么结论?有一个角和夹这个角的两边对应相等的两个
三角形全等(简写成“边角边”或“SAS”)∴ △ABC≌△A′B′C′ (SAS)练一练分别找出各题中的全等三角形40° DEF(1)(2)△ABC≌△EFD 根据“SAS”△ADC≌△CBA 根据“SAS”如图,AC与BD相交于点O。已知OA=OC,
OB=OD,说明△AOB≌△COD的理由。解:在△AOB和△COD中
OA=___ ( )
∠AOB=______( )
OB=OD ( )
∴ △AOB≌△COD( )
对顶角相等 OC ∠COD SAS已知已知如图,点D、E分别在AC、AB上。已知AB=AC,AD=AE,则BD=CE。请说明理由。ΔACEAE∠A∠A已知ΔABDΔACESAS全等三角形的对应边相等公共角已知:如图, AB=CB ,∠ ABD= ∠ CBD
△ ABD 和△ CBD 全等吗?
分析:△ ABD ≌△ CBDAB=CB(已知)∠ABD= ∠CBD(已知)?ABCD已知:如图, AB=CB ,∠ ABD= ∠ CBD 。
问AD=CD, BD 平分∠ ADC 吗?ABCD练习 (2) 已知:AD=CD, BD 平分∠ ADC 。
问∠A=∠ C 吗?归纳:判定两条线段相等或二个角相等
可以通过从它们所在的两个三角形全等而得到。自主合作探究互动2、如图,AB=CD,BC=AD,请说明∠A=∠C的道理。ACBOD垂直平分线定义
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线。∵ OC⊥AB
OA=OB
∴ OC是线段AB的垂直平分线解:当点C与点O重合时,
已知OA=OB,显然CA=CB;当点C与点O不重合时,∴CA=CB
(全等三角形对应边相等) 点C是线段AB的垂直平分线上的特殊的
点,还是任意的点?由此你能得到什么结论?线段垂直平分线 上的点到线段两端的距离相等。(中垂线的性质)如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。只要测量出AˊBˊ的长就知道内槽AB的宽。请说明理由。如图,有一湖的湖岸在A、B之间呈一段圆弧状,
A、B间的距离不能直接测得.你能用已学过的知
识或方法设计测量方案,求出A,B间的距离吗?AB—— 办法总比困难多!皮尺ABOCD如图,有一湖的湖岸在A、B之间呈一段
圆弧状,A、B间的距离不能直接测得.你
能用已学过的知识或方法设计测量方案,
求出A,B间的距离吗?— 我有办法了!探究新知 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。。AB 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。想一想 AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE
AB=DE小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。△EDH≌△FDH 根据“SAS”,所以EH=FH 以3cm,5cm为三角形的两边,长度为5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?ABCDEF5cm3cm40°40°3cm5cm结论:两边及其一边所对的角相等,两个三角形不一定全等探究2猜一猜:是不是两条边和一个角对应相等,这样的两个三角形一定全等吗?
你能举例说明吗?如图△ABC与△ABD中,AB=AB,AC=AD, ∠B=∠BΔABC和ΔABD全等吗?注:这个角一定要是这两边所夹的角故“边边角”(SSA)不能说明两个三角形是全等的。2、 线段垂直平分线的概念1、三角形全等的识别方法二:
有一个角和夹这个角的两边对应相等的两个三角形全等(简写成“边角边”或“SAS”)3、 线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等.星期天,小刚在家玩篮球,不小心将一块三角形玻璃摔坏了(如图所示)。情急之中,小刚量出了AB、BC的长,然后便去了玻璃店,他想重新裁得一块和原来一样的三角形玻璃。小刚能如愿吗?很快的,小刚到了玻璃店。不过,店员告诉他,虽然已经有了两边的长,但还是不能重新裁得一块和原来一样的三角形玻璃。于是,小刚向家里的弟弟打电话。请问:
小刚最少还需询问几个数据就
能如愿,数据可以是_______。1.5 三角形全等的条件(3)有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)回顾与思考三角形全等的条件1: 有一个角和夹这个角的两边对应相等的两个
三角形全等(简写成“边角边”或“SAS”)在△ABC和△A′B′C′中
AB=A′B′
∠ABC=∠A′B′C′
BC=B′C′
∴ △ABC≌△A′B′C(SAS)三角形全等的条件2:回顾与思考中垂线的性质
线段垂直平分线上的点到线段两端点的距离相等
练一练:①. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.10cm6cm议一议 小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?所带的这块玻璃里有几个条件已知? 有两个角和这两个角的夹边对应相等的两个三角形一定全等吗?请用量角器和刻度尺画ΔABC,使BC=3, ∠B=400、 ∠C=600 将你画的三角形与其他同学画的三角形比较,你发现了什么?CBA6004003cm 有两个角和这两个角的夹边对应相等的两个三角形全等。(简写成“角边角”或“ASA”) 剪下来,与同伴进行比较,它们能否互相重合?合作学习:∴ΔABC≌ΔA′B′C′(ASA) 有两个角和这两个角的夹边对应相等的两个三角形全等。(简写成“角边角”或“ASA”)数学语言表示:想一想:如图,在Δ ABC和Δ A/ B/ C/ 中,已知AB= A/ B/ ,∠B= ∠B /、 ∠C= ∠C / ,那么
Δ ABC与Δ A/ B/ C/ 会全等吗?请说明理由。 结论:两角和其中一角的对边对应相等的两个三角形全等。(简写成“角角边”或“AAS”) 能不能把“AAS”、“ASA”简述为“两角
和一边对应相等的两个三角形全等”? 在△ADE和△ABC中但△ABC和△ADE不全等
结论:说明两个三角形全等时,特别注意边和角“位置上对应相等” 。在△ABC和△DEF中
∠A=∠D
____=____
∠B=∠E
∴ △ABC≌△DEF(ASA)
AB DE填一填:在△ABC和△DEF中
____=____
AC=DF
____=____
∴ △ABC≌△DEF(ASA)
∠A ∠D∠C ∠F填一填:在△ABC和△DEF中
____=____
BC=EF
∠B=∠E
∴ △ABC≌△DEF(ASA)
∠C ∠F填一填:(AAS)∠A=∠D在△ABC和△DEF中
∠A=∠D
∠C=∠F
____=____
∴ △ABC≌△DEF(AAS)
填一填:BC=EF或AC=DF小试牛刀:1、如图∠ACB=∠DFE,BC=EF,根据ASA或AAS,那么应补充一个直接条件 --------------------------,(写出一个即可),才能使△ABC≌△DEF2、如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?ABCDEF∠B=∠E或∠A=∠D3、如图,∠1=∠2,∠3=∠4,说明:AC=ADABDABCABD ABC∠1=∠2 已知AB=AB∠ABD=∠ABC 已知ABD ABC ASAAC=AD例1、已知,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C,试说明AD=AE。解 :在△ADC和△AEB中∴AD=AE(全等三角形的对应边相等)O∴△ACD≌△ABE(ASA)例2、如图,点P是∠BAC的平分线上的一点,PB⊥AB,PC⊥AC。说明PB=PC的理由。角平分线上的点到角两边的距离相等。解:在△APB和△ APC中∠PAB=∠PAC∠ABP=∠ACPAP=AP(角平分线的意义)(垂线的意义)(公共边)∴ △APB≌△APC(AAS)∴PB=PC (根据什么?)数学语言表示:
∵AP是∠BAC的角平分线,
且PB⊥AB,PC⊥AC(已知)
∴PB=PC(角平分线上的点到角两边的距离相等)。(角平分线的性质) 1、如图,AB⊥BC,AD⊥DC,∠1=∠2。
求证:AB=AD巩固练习: 2、如图:要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长,为什么?巩固练习:判定条件全等三角形的定义
SSS
SAS
ASA(AAS)边和角分别对应相等,而不是分别相等。两个三角形全等特别注意:关键:找符合要求的条件 全课小结谈谈你的感受...1、已知:AC⊥CD,BD⊥CD,M是AB的中点,连CM并延长交BD于F,请说明:M是CF的中点.ACMDFBK拓展练习:2、如图, △ABC的两条高AD,BE相交于H,且AD=BD,试说明DH=DC.拓展练习:再见!
对应边所对的角是对应角。
(1)
(2)
(3) 两个全等三角形的位置变化了,对应边、对应角的大小有变化吗?由此你能得到什么结论?观察与思考那么有哪些边相等,哪些角相等? AB=DE ,BC=EF ,AC=DF答案:(AB=CD,AD=CB,BD=DB)答案:答案(A与D,B与C,C与E)活动二:右边的图形是一个等边三角形,你能把它分成两个全等的三角形吗?你能把它分成三个、四个全等的三角形吗?请试试看!例:如图,AD平分∠BAC,AB=AC.
△ABD与△ACD全等吗?BD与CD相等吗?
∠B与∠C呢?请说明理由。 本节课你学到了哪些知识?
你知道全等三角形有哪些性质吗?
你还想了解关于全等三角形的哪些知识?谈收获1.5 三角形全等的条件(一)知识回顾①AB=DE ② BC=EF ③ CA=FD ④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F2、 什么叫全等三角形?能够重合的两个三角形叫 全等三角形。3、 全等三角形有什么性质?1、什么叫全等图形?能够完全重合的两个图形叫做全等图形。全等三角形对应边相等,对应角相等。1、已知△ADF≌△CBE,则结论:①AF=CE ②∠1=∠2 ③BE=CF ④AE=CF,正确的个数是( )(A)1个(B)2个( C)3个(D)4个课前练习:C2、面积相等的两个三角形一定全等吗?课前练习:3、周长相等的两个三角形一定全等吗?课前练习:试问怎样的三角形才会全等呢?合作学习 1、已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画的进行比较,它们一定全等吗?(不一定全等) 2、已知一个三角形的三条边分别为4cm,5cm,7cm,你能画出这个三角形吗?合作学习画法:1、画线段AB=4cm;2、分别以A、B为圆心,5cm和7cm长为半径画两条圆弧,交于点C;3、连结AC、BC;△ABC就是所求的三角形。 把你画的三角形与同伴画的进行比较,它们一定全等吗? 已知三角形三条边分别是4cm,5cm,7cm,画出这个三角形AB=EFBC=FGAC=EG(SSS)有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)在△ABC和△EFG中用 数学语言表述: 用这样的结论可以判定两个三角形全等. 判断两个三角形全等的推理过程,叫做证明三角形全等. 由上面的结论可知,只要三角形三边长度确定了,这个三角形的形状和大小就完全确定了,三角形的这个性质叫做三角形的稳定性。三角形的稳定性:做一做 有一些长度适当的木条,用钉子把它们分别钉成三角形和四边形,并拉动它们。 三角形的大小和形状是固定不变的,而四边形
的形状会改变。 只要三角形三边的长度确定了,这个三角形的形
状和大小就确定,三角形的这个性质叫三角形的稳定性。 三角形的稳定性举例例1、如图,在四边形ABCD中,AB=CD,AD=CB,则∠A= ∠C,请说明理由。解:在△ABD和△CDB中,(已知)(已知)AB=CDAD=CBBD=DB(公共边)∴ △ABD ≌ △CDB(SSS)∴ ∠A= ∠C(根据什么?)证明:在△ABD和△ACD中,AB=AC(已知)
AD=AD(公共边)
DB=DC (已知)∴ △ ABD≌ △ACD(SSS) 如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架,请说明△ ABD≌ △ ACD的理由。牛刀小试分析:要证明△ ABD≌ △ ACD,首先看这两个三角形的三条边是否对应相等。牛刀小试 如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架,请说明△ ABD≌ △ ACD的理由。小结:从以上的解法中可以看出,说理要由题设(已知)出发,经过一步步的推理,最后推出正确的结论。∠1和∠2相等么?理由呢?能判断直线AD与直线BC的位置关系么?对于本题,你还能得到什么结论?例2、 已知∠BAC,用直尺和圆规∠BAC的角平分线AD,并说明正确的理由。以上是角平分线的尺规画法作法:
1、以点A为圆心,适当的长为半径,与角的两边分别交于E、F两点。3、过点A、D作射线AD。射线AD为所求的平分线。请同学们说说理由练一练: 已知∠α,用直尺和圆规作∠ α的平分线(只要求作出图形,并保留作图痕迹)α例3,如图,已知AB=CD,AD=CB,请说明∠B=∠D解:连结AC,AB=CD(已知)AC=AC(公共边)BC=AD(已知)∴ △ ABC≌ △ CDA(SSS)∴ ∠B=∠D(全等三角形对应角相等)问:此题添加辅助线,若连结BD行吗?在原有条件下,还能推出什么结论?在△ABC和△ ADC中小结:四边形问题转化为三角形问题解决。1、 如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 巩固练习:答: △ABC≌△DCB
理由如下:∵ 在△ABC和△DCB中AB = DCAC = DB=BCCB∴ △ABC≌△DCB(SSS)(公共边)(已知)(已知)2、如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?HDCBA解:有三组。 在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);在△ABH和△ACH中 ∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中 ∵BD=CD,BH=CH,DH=DH∴△DBH≌△DCH(SSS) 3、已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”说明△ABC ≌△ FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?解:要说明△ABC ≌△ FDE,还应该有AB=DF这个条件∵ DB是AB与DF的公共部分, 且AD=BF
∴ AD+DB=BF+DB
即 AB=DF4、 如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF。试说明∠A=∠D的理由。解:∵BE=CF(已知)即 BC=EF在△ABC和△DEF中AB=DE(已知)AC=BF(已知)BC=EF(已证)∴△ABC≌△DEF(SSS)∴∠A=∠D(全等三角形对应角相等)小结:欲想说明角相等,先转化为说明三角形全等。∴ BE+EC=CF+EC2. 如图, 在△ABC中,AB=AC, AD是BC边上的中线,则AD⊥BC. ABCD解:∵AD是BC边上的中线∴BD=CD在△ABD和△ACD中AB=AC ( )BD=CD ( )AD=AD ( )已知已证公共边∴△ABD≌△ACD ( )SSS∴∠ADB=∠ADC ( )全等三角形的对应角相等∵∠ADB+∠ADC=180°∴∠ADB=90°,∴AD⊥BC 5、 如图,AB=AC,AE=AD,BD=CE,请说明△AEB ≌ △ ADC的理由。解:∵BD=CE
∴ BD-ED=CE-ED,
即BE=CD。在AEB和ADC中,
AB=AC
AE=AD
BE=CD
∴ △AEB ≌ △ ADC(SSS)(已知)(已知)(已证)请同学们谈谈本节课的收获与体会本节课你学到了什么?
发现了什么?
有什么收获?
还存在什么没有解决的问题? 再 见!要判定两个三角形全等我们已经学过几种方法:1.能完全重合的两个三角形是全等三角形2.有三条边对应相等的两个三角形全等(简称SSS)要判定两个三角形全等还有其它方法吗?1.5 三角形全等的条件(2)创设情景 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。怎样测出A、B两杆之间的距离呢?。AB知识回顾 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。探究1对于三个角对应相等的两个三角形全等吗?如图, △ABC和△ADE中,如果 DE∥AB,则∠A=∠A,∠B=∠ADE,∠C= ∠ AED,但△ABC和△ADE不重合,所以不全等。三个角对应相等的两个三角形不一定全等做一做: 有一个△ABC,它的两边边长分别为3cm、4cm,任意再画一个三角形, 使AB=3cm,AC=4cm。这样画出来的两个三角形进行比较,
它们互相重合吗?画法:2. 在射线AM上截取AB= 3cm3. 在射线AN上截取AC=4cm 若再加一个条件,使∠A=45°,画出△ABC1. 画∠MAN= 45°4.连接BC∴△ABC就是所求的三角形把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?探究2画一画,比一比:让我们动手做一做:用量角器和刻度尺画ΔABC,
使 AB=4cm,BC=6cm,∠ABC=60° 将你画出的三角形和其他同学画的三角形进行比较,它们互相重合吗?由此,你得到了什么结论?有一个角和夹这个角的两边对应相等的两个
三角形全等(简写成“边角边”或“SAS”)∴ △ABC≌△A′B′C′ (SAS)练一练分别找出各题中的全等三角形40° DEF(1)(2)△ABC≌△EFD 根据“SAS”△ADC≌△CBA 根据“SAS”如图,AC与BD相交于点O。已知OA=OC,
OB=OD,说明△AOB≌△COD的理由。解:在△AOB和△COD中
OA=___ ( )
∠AOB=______( )
OB=OD ( )
∴ △AOB≌△COD( )
对顶角相等 OC ∠COD SAS已知已知如图,点D、E分别在AC、AB上。已知AB=AC,AD=AE,则BD=CE。请说明理由。ΔACEAE∠A∠A已知ΔABDΔACESAS全等三角形的对应边相等公共角已知:如图, AB=CB ,∠ ABD= ∠ CBD
△ ABD 和△ CBD 全等吗?
分析:△ ABD ≌△ CBDAB=CB(已知)∠ABD= ∠CBD(已知)?ABCD已知:如图, AB=CB ,∠ ABD= ∠ CBD 。
问AD=CD, BD 平分∠ ADC 吗?ABCD练习 (2) 已知:AD=CD, BD 平分∠ ADC 。
问∠A=∠ C 吗?归纳:判定两条线段相等或二个角相等
可以通过从它们所在的两个三角形全等而得到。自主合作探究互动2、如图,AB=CD,BC=AD,请说明∠A=∠C的道理。ACBOD垂直平分线定义
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线。∵ OC⊥AB
OA=OB
∴ OC是线段AB的垂直平分线解:当点C与点O重合时,
已知OA=OB,显然CA=CB;当点C与点O不重合时,∴CA=CB
(全等三角形对应边相等) 点C是线段AB的垂直平分线上的特殊的
点,还是任意的点?由此你能得到什么结论?线段垂直平分线 上的点到线段两端的距离相等。(中垂线的性质)如图,把两根钢条AAˊ,BBˊ的中点连在一起,可以做成一个测量工件内槽宽的卡钳。只要测量出AˊBˊ的长就知道内槽AB的宽。请说明理由。如图,有一湖的湖岸在A、B之间呈一段圆弧状,
A、B间的距离不能直接测得.你能用已学过的知
识或方法设计测量方案,求出A,B间的距离吗?AB—— 办法总比困难多!皮尺ABOCD如图,有一湖的湖岸在A、B之间呈一段
圆弧状,A、B间的距离不能直接测得.你
能用已学过的知识或方法设计测量方案,
求出A,B间的距离吗?— 我有办法了!探究新知 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。。AB 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。想一想 AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE
AB=DE小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。△EDH≌△FDH 根据“SAS”,所以EH=FH 以3cm,5cm为三角形的两边,长度为5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?ABCDEF5cm3cm40°40°3cm5cm结论:两边及其一边所对的角相等,两个三角形不一定全等探究2猜一猜:是不是两条边和一个角对应相等,这样的两个三角形一定全等吗?
你能举例说明吗?如图△ABC与△ABD中,AB=AB,AC=AD, ∠B=∠BΔABC和ΔABD全等吗?注:这个角一定要是这两边所夹的角故“边边角”(SSA)不能说明两个三角形是全等的。2、 线段垂直平分线的概念1、三角形全等的识别方法二:
有一个角和夹这个角的两边对应相等的两个三角形全等(简写成“边角边”或“SAS”)3、 线段垂直平分线的性质:线段垂直平分线上的点到线段两端点的距离相等.星期天,小刚在家玩篮球,不小心将一块三角形玻璃摔坏了(如图所示)。情急之中,小刚量出了AB、BC的长,然后便去了玻璃店,他想重新裁得一块和原来一样的三角形玻璃。小刚能如愿吗?很快的,小刚到了玻璃店。不过,店员告诉他,虽然已经有了两边的长,但还是不能重新裁得一块和原来一样的三角形玻璃。于是,小刚向家里的弟弟打电话。请问:
小刚最少还需询问几个数据就
能如愿,数据可以是_______。1.5 三角形全等的条件(3)有三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)回顾与思考三角形全等的条件1: 有一个角和夹这个角的两边对应相等的两个
三角形全等(简写成“边角边”或“SAS”)在△ABC和△A′B′C′中
AB=A′B′
∠ABC=∠A′B′C′
BC=B′C′
∴ △ABC≌△A′B′C(SAS)三角形全等的条件2:回顾与思考中垂线的性质
线段垂直平分线上的点到线段两端点的距离相等
练一练:①. 如图(1), △ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是______.10cm6cm议一议 小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?所带的这块玻璃里有几个条件已知? 有两个角和这两个角的夹边对应相等的两个三角形一定全等吗?请用量角器和刻度尺画ΔABC,使BC=3, ∠B=400、 ∠C=600 将你画的三角形与其他同学画的三角形比较,你发现了什么?CBA6004003cm 有两个角和这两个角的夹边对应相等的两个三角形全等。(简写成“角边角”或“ASA”) 剪下来,与同伴进行比较,它们能否互相重合?合作学习:∴ΔABC≌ΔA′B′C′(ASA) 有两个角和这两个角的夹边对应相等的两个三角形全等。(简写成“角边角”或“ASA”)数学语言表示:想一想:如图,在Δ ABC和Δ A/ B/ C/ 中,已知AB= A/ B/ ,∠B= ∠B /、 ∠C= ∠C / ,那么
Δ ABC与Δ A/ B/ C/ 会全等吗?请说明理由。 结论:两角和其中一角的对边对应相等的两个三角形全等。(简写成“角角边”或“AAS”) 能不能把“AAS”、“ASA”简述为“两角
和一边对应相等的两个三角形全等”? 在△ADE和△ABC中但△ABC和△ADE不全等
结论:说明两个三角形全等时,特别注意边和角“位置上对应相等” 。在△ABC和△DEF中
∠A=∠D
____=____
∠B=∠E
∴ △ABC≌△DEF(ASA)
AB DE填一填:在△ABC和△DEF中
____=____
AC=DF
____=____
∴ △ABC≌△DEF(ASA)
∠A ∠D∠C ∠F填一填:在△ABC和△DEF中
____=____
BC=EF
∠B=∠E
∴ △ABC≌△DEF(ASA)
∠C ∠F填一填:(AAS)∠A=∠D在△ABC和△DEF中
∠A=∠D
∠C=∠F
____=____
∴ △ABC≌△DEF(AAS)
填一填:BC=EF或AC=DF小试牛刀:1、如图∠ACB=∠DFE,BC=EF,根据ASA或AAS,那么应补充一个直接条件 --------------------------,(写出一个即可),才能使△ABC≌△DEF2、如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?ABCDEF∠B=∠E或∠A=∠D3、如图,∠1=∠2,∠3=∠4,说明:AC=ADABDABCABD ABC∠1=∠2 已知AB=AB∠ABD=∠ABC 已知ABD ABC ASAAC=AD例1、已知,点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C,试说明AD=AE。解 :在△ADC和△AEB中∴AD=AE(全等三角形的对应边相等)O∴△ACD≌△ABE(ASA)例2、如图,点P是∠BAC的平分线上的一点,PB⊥AB,PC⊥AC。说明PB=PC的理由。角平分线上的点到角两边的距离相等。解:在△APB和△ APC中∠PAB=∠PAC∠ABP=∠ACPAP=AP(角平分线的意义)(垂线的意义)(公共边)∴ △APB≌△APC(AAS)∴PB=PC (根据什么?)数学语言表示:
∵AP是∠BAC的角平分线,
且PB⊥AB,PC⊥AC(已知)
∴PB=PC(角平分线上的点到角两边的距离相等)。(角平分线的性质) 1、如图,AB⊥BC,AD⊥DC,∠1=∠2。
求证:AB=AD巩固练习: 2、如图:要测量河两岸相对的两点A,B的距离,可以在AB的垂线BF上取两点C,D,使BC=CD,再定出BF的垂线DE,使A,C,E在一条直线上,这时测得DE的长就是AB的长,为什么?巩固练习:判定条件全等三角形的定义
SSS
SAS
ASA(AAS)边和角分别对应相等,而不是分别相等。两个三角形全等特别注意:关键:找符合要求的条件 全课小结谈谈你的感受...1、已知:AC⊥CD,BD⊥CD,M是AB的中点,连CM并延长交BD于F,请说明:M是CF的中点.ACMDFBK拓展练习:2、如图, △ABC的两条高AD,BE相交于H,且AD=BD,试说明DH=DC.拓展练习:再见!
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
