1.1锐角三角函数达标练习(无答案) 浙教版九年级数学下册
文档属性
| 名称 | 1.1锐角三角函数达标练习(无答案) 浙教版九年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 564.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-02 00:00:00 | ||
图片预览

文档简介
1.1锐角三角函数达标练习
班级:________ 姓名:________
一、单选题(共 8 小题)
1、如图,在菱形ABCD中,,M是对角线BD上的一个动点,,则的最小值为( )
A.1 B. C. D.2
2、如图,菱形ABCD中,AB=2,∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )
A. B. C. D.3
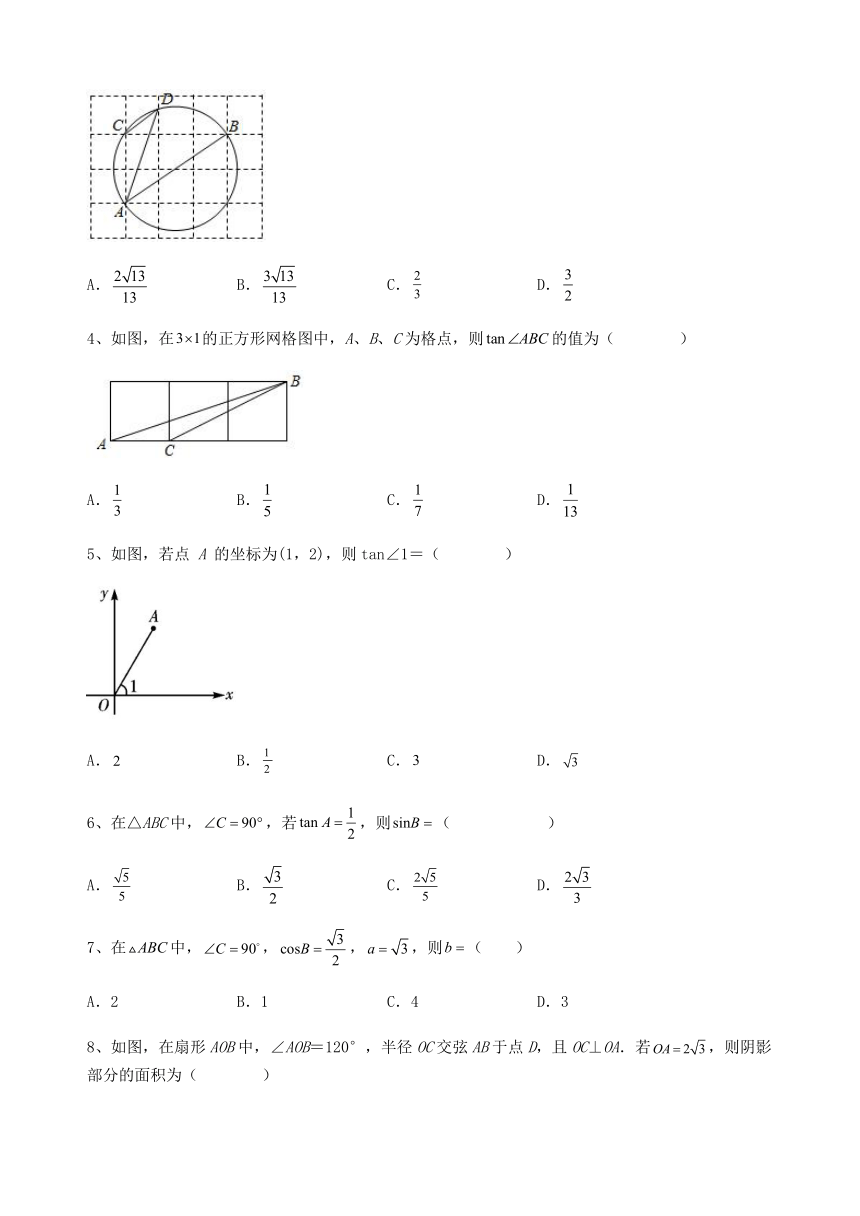
3、如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则的值为( )
A. B. C. D.
4、如图,在的正方形网格图中,A、B、C为格点,则的值为( )
A. B. C. D.
5、如图,若点 A 的坐标为(1,2),则tan∠1=( )
A. B. C. D.
6、在△ABC中,,若,则( )
A. B. C. D.
7、在中,,,,则( )
A.2 B.1 C.4 D.3
8、如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若,则阴影部分的面积为( )
A. B. C. D.
二、填空题(共 8 小题)
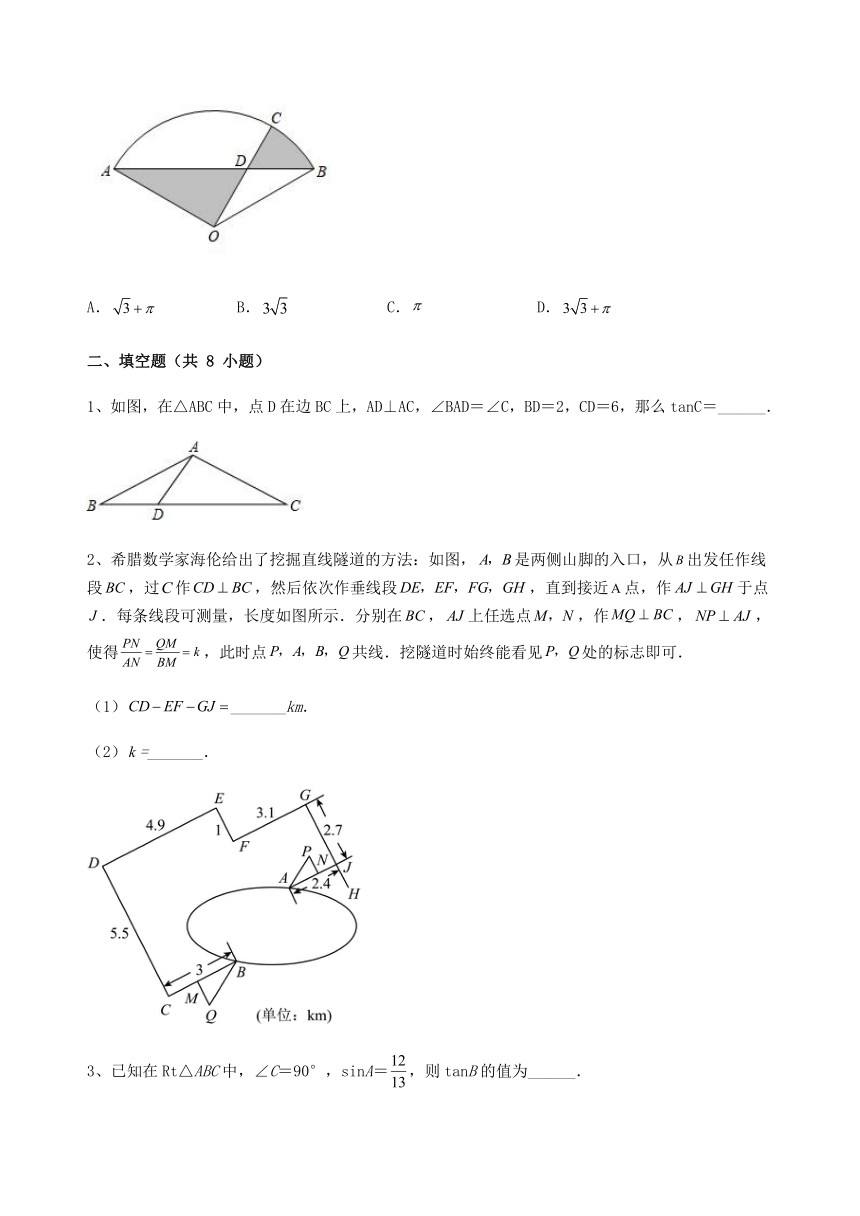
1、如图,在△ABC中,点D在边BC上,AD⊥AC,∠BAD=∠C,BD=2,CD=6,那么tanC=______.
2、希腊数学家海伦给出了挖掘直线隧道的方法:如图,是两侧山脚的入口,从出发任作线段,过作,然后依次作垂线段,直到接近点,作于点.每条线段可测量,长度如图所示.分别在,上任选点,作,,使得,此时点共线.挖隧道时始终能看见处的标志即可.
(1)_______km.
(2)=_______.
3、已知在Rt△ABC中,∠C=90°,sinA=,则tanB的值为______.
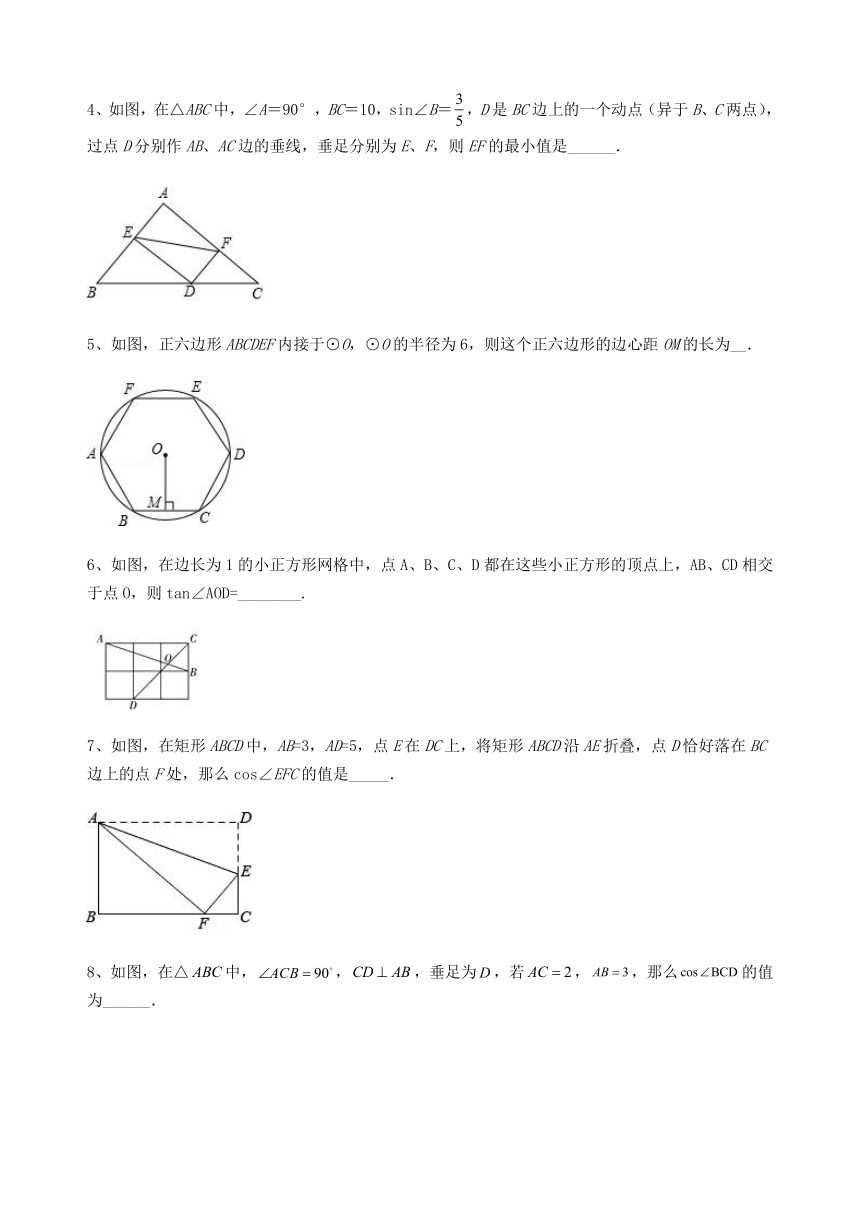
4、如图,在△ABC中,∠A=90°,BC=10,sin∠B=,D是BC边上的一个动点(异于B、C两点),过点D分别作AB、AC边的垂线,垂足分别为E、F,则EF的最小值是______.
5、如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为__.
6、如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=________.
7、如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是_____.
8、如图,在△中,,,垂足为,若,,那么的值为______.
三、解答题(共 6 小题)
1、如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面D处测得楼房顶部A的仰角为30°,沿坡面向下走到坡脚C处,然后在地面上沿CB向楼房方向继续行走10米到达E处,测得楼房顶部A的仰角为60°.已知坡面CD=10米,山坡的坡度i=1:(坡度是指坡面的铅直高度与水平宽度的比).求楼房AB高度.(结果保留根式)
2、如图,在平面直角坐标系中,的三个顶点坐标分别是,,.
(1)将向左平移4个单位长度后得到,请画出;
(2)以点为位似中心,在轴的左侧画出的位似图形,使与的位似比为1:2;
(3)请直接写出的值.
3、第24届冬奥会(也称2022年北京冬奥会)于2022年2月4日至2月20日在中国北京举行,北京成为了历史上第一座既举办过夏奥会又举办过冬奥会的城市.冬奥会上跳台滑雪是一项极为壮观的运动.运动员经过助滑、起跳、空中飞行和着陆,整个动作连贯一致,一气呵成,如图,某运动员穿着滑雪板,经过助滑后,从倾斜角的跳台A点以速度沿水平方向跳出,若忽略空气阻力影响,水平方向速度将保持不变.同时,由于受重力作用,运动员沿竖直方向会加速下落,因此,运动员在空中飞行的路线是抛物线的一部分,已知该运动员在B点着陆,,且.忽略空气阻力,请回答下列问题:
(1)求该运动员从跳出到着陆垂直下降了多少m?
(2)以A为坐标原点建立直角坐标系,求该抛物线表达式;
(3)若该运动员在空中共飞行了4s,求他飞行2s后,垂直下降了多少m?
4、如图,已知矩形ABCD中,对角线AC、BD相交于点O,过点A作AEBD,交CB的延长线于点E.
(1)求证:AE=AC;
(2)若cos∠E=,CE=12,求矩形ABCD的面积.
5、如图,在△ABC中,AC=BC,AB=12,tan∠A=.
(1)尺规作图:以AC为直径作⊙O,与AB交于点D(不写作法,保留作图痕迹);
(2)求⊙O的半径长度.
6、如图,已知抛物线的对称轴为直线x=1,与x轴的一个交点为,顶点为B.点在抛物线上,直线BC交x轴于点E.
(1)求抛物线的表达式及点E的坐标;
(2)连接AB,求∠B的余切值;
(3)点G为线段AC上一点,过点G作CB的垂线交x轴于点M(位于点E右侧),当△CGM与△ABE相似时,求点M的坐标.
班级:________ 姓名:________
一、单选题(共 8 小题)
1、如图,在菱形ABCD中,,M是对角线BD上的一个动点,,则的最小值为( )
A.1 B. C. D.2
2、如图,菱形ABCD中,AB=2,∠ABC=60°,矩形BEFG的边EF经过点C,且点G在边AD上,若BG=4,则BE的长为( )
A. B. C. D.3
3、如图,由边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C、D,则的值为( )
A. B. C. D.
4、如图,在的正方形网格图中,A、B、C为格点,则的值为( )
A. B. C. D.
5、如图,若点 A 的坐标为(1,2),则tan∠1=( )
A. B. C. D.
6、在△ABC中,,若,则( )
A. B. C. D.
7、在中,,,,则( )
A.2 B.1 C.4 D.3
8、如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥OA.若,则阴影部分的面积为( )
A. B. C. D.
二、填空题(共 8 小题)
1、如图,在△ABC中,点D在边BC上,AD⊥AC,∠BAD=∠C,BD=2,CD=6,那么tanC=______.
2、希腊数学家海伦给出了挖掘直线隧道的方法:如图,是两侧山脚的入口,从出发任作线段,过作,然后依次作垂线段,直到接近点,作于点.每条线段可测量,长度如图所示.分别在,上任选点,作,,使得,此时点共线.挖隧道时始终能看见处的标志即可.
(1)_______km.
(2)=_______.
3、已知在Rt△ABC中,∠C=90°,sinA=,则tanB的值为______.
4、如图,在△ABC中,∠A=90°,BC=10,sin∠B=,D是BC边上的一个动点(异于B、C两点),过点D分别作AB、AC边的垂线,垂足分别为E、F,则EF的最小值是______.
5、如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM的长为__.
6、如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=________.
7、如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是_____.
8、如图,在△中,,,垂足为,若,,那么的值为______.
三、解答题(共 6 小题)
1、如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面D处测得楼房顶部A的仰角为30°,沿坡面向下走到坡脚C处,然后在地面上沿CB向楼房方向继续行走10米到达E处,测得楼房顶部A的仰角为60°.已知坡面CD=10米,山坡的坡度i=1:(坡度是指坡面的铅直高度与水平宽度的比).求楼房AB高度.(结果保留根式)
2、如图,在平面直角坐标系中,的三个顶点坐标分别是,,.
(1)将向左平移4个单位长度后得到,请画出;
(2)以点为位似中心,在轴的左侧画出的位似图形,使与的位似比为1:2;
(3)请直接写出的值.
3、第24届冬奥会(也称2022年北京冬奥会)于2022年2月4日至2月20日在中国北京举行,北京成为了历史上第一座既举办过夏奥会又举办过冬奥会的城市.冬奥会上跳台滑雪是一项极为壮观的运动.运动员经过助滑、起跳、空中飞行和着陆,整个动作连贯一致,一气呵成,如图,某运动员穿着滑雪板,经过助滑后,从倾斜角的跳台A点以速度沿水平方向跳出,若忽略空气阻力影响,水平方向速度将保持不变.同时,由于受重力作用,运动员沿竖直方向会加速下落,因此,运动员在空中飞行的路线是抛物线的一部分,已知该运动员在B点着陆,,且.忽略空气阻力,请回答下列问题:
(1)求该运动员从跳出到着陆垂直下降了多少m?
(2)以A为坐标原点建立直角坐标系,求该抛物线表达式;
(3)若该运动员在空中共飞行了4s,求他飞行2s后,垂直下降了多少m?
4、如图,已知矩形ABCD中,对角线AC、BD相交于点O,过点A作AEBD,交CB的延长线于点E.
(1)求证:AE=AC;
(2)若cos∠E=,CE=12,求矩形ABCD的面积.
5、如图,在△ABC中,AC=BC,AB=12,tan∠A=.
(1)尺规作图:以AC为直径作⊙O,与AB交于点D(不写作法,保留作图痕迹);
(2)求⊙O的半径长度.
6、如图,已知抛物线的对称轴为直线x=1,与x轴的一个交点为,顶点为B.点在抛物线上,直线BC交x轴于点E.
(1)求抛物线的表达式及点E的坐标;
(2)连接AB,求∠B的余切值;
(3)点G为线段AC上一点,过点G作CB的垂线交x轴于点M(位于点E右侧),当△CGM与△ABE相似时,求点M的坐标.
