浙教版数学七年级上册 5.4.1 希望工程义演与行程问题 课件(共20张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 5.4.1 希望工程义演与行程问题 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 378.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-05 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第5章 一元一次方程
5.4 一元一次方程的应用
第1课时 希望工程义演与行程问题
教学目标
1.体验方程是刻画现实世界的有效的数学模型.
2.掌握列方程解应用题的一般步骤.
3.会利用一元一次方程解决简单的实际问题.
情景导入
某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹得票款6950元.成人票与学生票各售出多少张?
成人票 8元
学生票 5元
思考:上面问题中包含哪些已知量、未知量和等量关系?
情景一:希望工程义演
【分析】已知量:总票数( )、总票款( )、成人票单价( )、学生票单价( );
未知量:成人票数、学生票数、成人票款、学生票款;
等量关系:
1000张
6950元
8元
5元
(1)学生票数+成人票数=1000张;
(2)学生票款+成人票款=6950元.
探究新知
解:设售出的学生票为x张,则售出的成人票为1000-x张
根据等量关系:_________________________,
可列出方程:
解得x= 350.
因此,售出学生票350张,成人票650张.
5x+8(1000- x)= 6950
你还有其他设法吗?
学生票款+成人票款=6950元
成人票:1000-350=650
设所得的学生票款为y元,则售出的成人票款为6950-y
根据等量关系:__________________________,
可列出方程:
解得y=1750.
因此,售出学生票350张,成人票650张.
学生票数+成人票数=1000张
1750÷5=350,1000-350=650
方法2:
(1)在复杂问题中要选择恰当、灵活的设未知数的方法,利于快速解题.
(2)当遇到含有两个未知量,两个等量关系时,可以把其中一个未知量设为未知数,另一个未知量就用其中的一个等量关系表示为代数式,用另一个等量关系来列方程.
规律总结
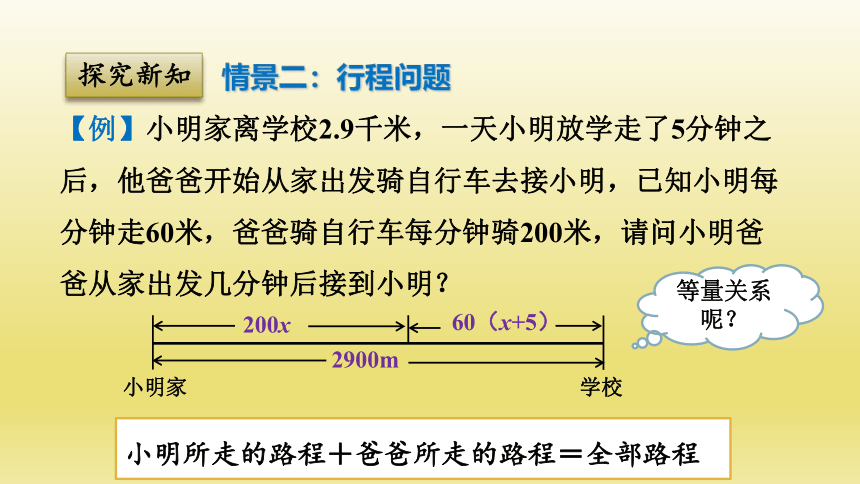
【例】小明家离学校2.9千米,一天小明放学走了5分钟之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60米,爸爸骑自行车每分钟骑200米,请问小明爸爸从家出发几分钟后接到小明?
【分析】设爸爸从家出发x分钟后接到小明,思考两人运动的特点以及已知量,未知量之间的关系,画出线段图.
探究新知
情景二:行程问题
【例】小明家离学校2.9千米,一天小明放学走了5分钟之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60米,爸爸骑自行车每分钟骑200米,请问小明爸爸从家出发几分钟后接到小明?
探究新知
情景二:行程问题
200x
60(x+5)
2900m
小明家
学校
等量关系呢?
小明所走的路程+爸爸所走的路程=全部路程
解:设小明爸爸出发x分钟后接到小明,
由题意,得 200x+60(x+5)=2900.
解得 x=10.
答:小明爸爸从家出发10分钟后接到小明.
【例】小明家离学校2.9千米,一天小明放学走了5分钟之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60米,爸爸骑自行车每分钟骑200米,请问小明爸爸从家出发几分钟后接到小明?
三个连续奇数的和为57,求这三个数.
解:设三个连续的奇数分别为x-2,x,x+2,
由题意,得(x-2)+x+(x+2)=57.
解得 x=19.
所以这三个连续奇数分别为17,19,21.
典例精析
数字问题
【分析】设方框内其中一个日期为x,则这个方框内所围成的4个日期为:
日历问题
典例精析
从如图的月历表中取一个2×2方块.若这个方块所围成的4个方格的日期之和为44,求这4个方格中的日期.
x x+1
x+7 x+8
解:设方框内数分别为x,x+1,x+7,x+8,
由题意,得x+(x+1)+(x+7)+(x+8)=44,
解得 x=7
所以4个方格的日期为7,8,14,15.
日历问题
典例精析
从如图的月历表中取一个2×2方块.若这个方块所围成的4个方格的日期之和为44,求这4个方格中的日期.
1、敌我两军相距25km,敌军以5km/h的速度逃跑,我军同时以8km/h的速度追击,并在相距1km处发生战斗.问战斗是在开始追击后几小时发生的?
想一想,线段图怎么画?
25km
5x
8x
我军
敌军
1km
我军
敌军
题中的等量关系是?
我军追击路程=敌军逃跑路程+25km-1km
巩固练习
解:设战斗是在开始追击后x小时发生的.
根据题意,得8x=5x+25-1.
解得 x=8.
答:战斗是在开始追击后8小时发生的.
1、敌我两军相距25km,敌军以5km/h的速度逃跑,我军同时以8km/h的速度追击,并在相距1km处发生战斗.问战斗是在开始追击后几小时发生的?
2.某希望中学为办公室安装电灯,准备一个办公室装五个灯泡,其中有40瓦和60瓦两种,总的瓦数是260瓦,则40瓦和60瓦的灯泡各装多少个?
解:设40瓦的灯泡装x个,则60瓦的灯泡装(5-x)个,
可列出方程:40x+60(5-x)=260,
解得x=2,
5-2=3(个).
答:40瓦的灯泡装2个,60瓦的灯泡装3个.
3.一班有40位同学,新年时开晚会,班主任到超市花了115元买果冻与巧克力共40个,若果冻每2个5元,巧克力每块3元,则班主任分别买了多少果冻和巧克力?
思考:用一元一次方程解决实际问题的一般步骤是什么?
实际问题
数学问题
(一元一次方程)
实际问题的解
数学问题的解
(一元一次方程的解)
抽象
寻找等量关系
解方程
解释
验证
课堂总结
(1)审题:分析题意,找出题中的数量关系;
(2)设元:选择一个合适的未知数用字母表示(注意单位名称);
(3)列方程:依据找到的等量关系,列出方程;
(4)解方程:求出方程的解(对间接设的未知数切记继续求解);
(5)检验:检查求出的值是否正确,并检验是否符合实际问题;
(6)答:写出答案(注意单位名称).
列一元一次方程解决实际问题的一般步骤:
谢谢观看
第5章 一元一次方程
5.4 一元一次方程的应用
第1课时 希望工程义演与行程问题
教学目标
1.体验方程是刻画现实世界的有效的数学模型.
2.掌握列方程解应用题的一般步骤.
3.会利用一元一次方程解决简单的实际问题.
情景导入
某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹得票款6950元.成人票与学生票各售出多少张?
成人票 8元
学生票 5元
思考:上面问题中包含哪些已知量、未知量和等量关系?
情景一:希望工程义演
【分析】已知量:总票数( )、总票款( )、成人票单价( )、学生票单价( );
未知量:成人票数、学生票数、成人票款、学生票款;
等量关系:
1000张
6950元
8元
5元
(1)学生票数+成人票数=1000张;
(2)学生票款+成人票款=6950元.
探究新知
解:设售出的学生票为x张,则售出的成人票为1000-x张
根据等量关系:_________________________,
可列出方程:
解得x= 350.
因此,售出学生票350张,成人票650张.
5x+8(1000- x)= 6950
你还有其他设法吗?
学生票款+成人票款=6950元
成人票:1000-350=650
设所得的学生票款为y元,则售出的成人票款为6950-y
根据等量关系:__________________________,
可列出方程:
解得y=1750.
因此,售出学生票350张,成人票650张.
学生票数+成人票数=1000张
1750÷5=350,1000-350=650
方法2:
(1)在复杂问题中要选择恰当、灵活的设未知数的方法,利于快速解题.
(2)当遇到含有两个未知量,两个等量关系时,可以把其中一个未知量设为未知数,另一个未知量就用其中的一个等量关系表示为代数式,用另一个等量关系来列方程.
规律总结
【例】小明家离学校2.9千米,一天小明放学走了5分钟之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60米,爸爸骑自行车每分钟骑200米,请问小明爸爸从家出发几分钟后接到小明?
【分析】设爸爸从家出发x分钟后接到小明,思考两人运动的特点以及已知量,未知量之间的关系,画出线段图.
探究新知
情景二:行程问题
【例】小明家离学校2.9千米,一天小明放学走了5分钟之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60米,爸爸骑自行车每分钟骑200米,请问小明爸爸从家出发几分钟后接到小明?
探究新知
情景二:行程问题
200x
60(x+5)
2900m
小明家
学校
等量关系呢?
小明所走的路程+爸爸所走的路程=全部路程
解:设小明爸爸出发x分钟后接到小明,
由题意,得 200x+60(x+5)=2900.
解得 x=10.
答:小明爸爸从家出发10分钟后接到小明.
【例】小明家离学校2.9千米,一天小明放学走了5分钟之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60米,爸爸骑自行车每分钟骑200米,请问小明爸爸从家出发几分钟后接到小明?
三个连续奇数的和为57,求这三个数.
解:设三个连续的奇数分别为x-2,x,x+2,
由题意,得(x-2)+x+(x+2)=57.
解得 x=19.
所以这三个连续奇数分别为17,19,21.
典例精析
数字问题
【分析】设方框内其中一个日期为x,则这个方框内所围成的4个日期为:
日历问题
典例精析
从如图的月历表中取一个2×2方块.若这个方块所围成的4个方格的日期之和为44,求这4个方格中的日期.
x x+1
x+7 x+8
解:设方框内数分别为x,x+1,x+7,x+8,
由题意,得x+(x+1)+(x+7)+(x+8)=44,
解得 x=7
所以4个方格的日期为7,8,14,15.
日历问题
典例精析
从如图的月历表中取一个2×2方块.若这个方块所围成的4个方格的日期之和为44,求这4个方格中的日期.
1、敌我两军相距25km,敌军以5km/h的速度逃跑,我军同时以8km/h的速度追击,并在相距1km处发生战斗.问战斗是在开始追击后几小时发生的?
想一想,线段图怎么画?
25km
5x
8x
我军
敌军
1km
我军
敌军
题中的等量关系是?
我军追击路程=敌军逃跑路程+25km-1km
巩固练习
解:设战斗是在开始追击后x小时发生的.
根据题意,得8x=5x+25-1.
解得 x=8.
答:战斗是在开始追击后8小时发生的.
1、敌我两军相距25km,敌军以5km/h的速度逃跑,我军同时以8km/h的速度追击,并在相距1km处发生战斗.问战斗是在开始追击后几小时发生的?
2.某希望中学为办公室安装电灯,准备一个办公室装五个灯泡,其中有40瓦和60瓦两种,总的瓦数是260瓦,则40瓦和60瓦的灯泡各装多少个?
解:设40瓦的灯泡装x个,则60瓦的灯泡装(5-x)个,
可列出方程:40x+60(5-x)=260,
解得x=2,
5-2=3(个).
答:40瓦的灯泡装2个,60瓦的灯泡装3个.
3.一班有40位同学,新年时开晚会,班主任到超市花了115元买果冻与巧克力共40个,若果冻每2个5元,巧克力每块3元,则班主任分别买了多少果冻和巧克力?
思考:用一元一次方程解决实际问题的一般步骤是什么?
实际问题
数学问题
(一元一次方程)
实际问题的解
数学问题的解
(一元一次方程的解)
抽象
寻找等量关系
解方程
解释
验证
课堂总结
(1)审题:分析题意,找出题中的数量关系;
(2)设元:选择一个合适的未知数用字母表示(注意单位名称);
(3)列方程:依据找到的等量关系,列出方程;
(4)解方程:求出方程的解(对间接设的未知数切记继续求解);
(5)检验:检查求出的值是否正确,并检验是否符合实际问题;
(6)答:写出答案(注意单位名称).
列一元一次方程解决实际问题的一般步骤:
谢谢观看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
