浙教版数学七年级上册 4.1 用字母表示数 课件(共15张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 4.1 用字母表示数 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 400.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-06 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
第4章 代数式
4.1 用字母表示数
运 算 定 律 字 母 表 示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b) +c= a +(b + c)
a×b = b×a
(a×b)×c =a×(b×c)
(a + b) ×c =a×c+b×c
复习旧知
你还记得如何用字母表示运算律吗?
探究新知
1只青蛙,1张嘴,2只眼睛,4条腿,1声扑通跳下水;
2只青蛙,2张嘴,4只眼睛,8条腿,2声扑通跳下水.
......
根据此儿歌:
(1)如果青蛙有10只,100只,500只,那么这首儿歌该怎么唱?
(2)如果青蛙的只数用字母n表示,那么这首儿歌又该怎么唱?
解:(1)把青蛙的只数一般化地用字母表示,找出嘴、眼睛、腿、入水响声与只数的关系,代入儿歌即可.
(2)n只青蛙n张嘴,2×n只眼睛,4×n条腿,n声扑通跳下水.
字母可以表示数量关系.
【例1】今日菜市场上的萝卜每千克a元,白菜每千克b元.某食堂要买30kg萝卜,50kg白菜,怎样表示今日要买的萝卜、白菜的总价?
解:要买的萝卜、白菜的总价=萝卜的数量×萝卜的单价+白菜的数量×白菜的单价,所以要买的萝卜、白菜的总价为(30×a+50×b)元,即(30a+50)b元.
注意书写要求:
1.数和表示数的字母相乘,或字母和字母相乘时,乘号可以不写,或用“·”来代替;
2.数和字母相乘,在省略乘号时,要把数字写在字母的前面;
3.数字因数是1或-1时,“1”通常省略不写;
4.带分数和字母相乘时,要把带分数化为假分数;
5.含有字母的除法写成分数的形式.
6.式子后面有单位且式子是和或差的形式时,把式子用括号括起来.
a
a
a
b
a
h
a
h
a
h
b
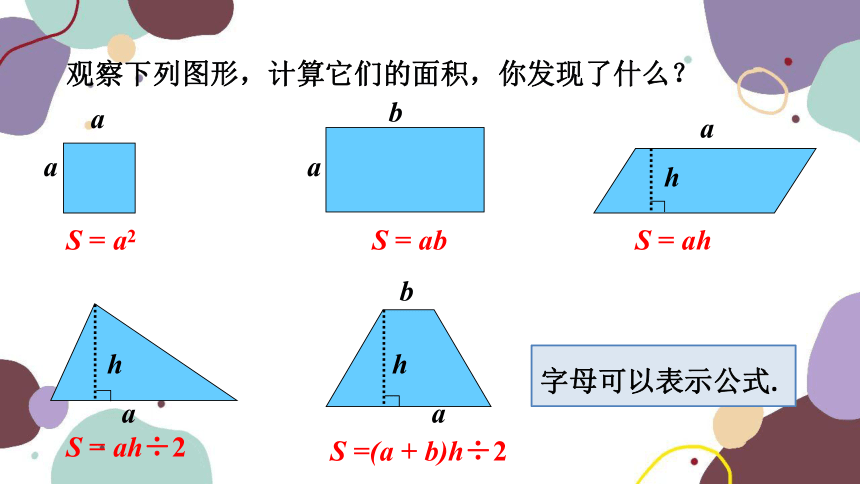
S = a2
S = ab
S = ah
S = ah÷2
S =(a + b)h÷2
观察下列图形,计算它们的面积,你发现了什么?
字母可以表示公式.
【例2】(1)长方形的长是a米,宽是3米,则面积是多少平方米?周长是多少米?
(2)下面表述中,字母表示什么?①圆的面积是πr2;②正方形的周长是4a.
解:(1)长方形的面积是3a平方米,周长是(a+3)×2米,即(2a+6)米.
(2)①r表示圆的半径;②a表示正方形的边长.
你还记得相反数的定义吗?你能用字母表示互为相反数的两数之间的关系吗?
解:相反数的定义:如果两个数只有符号不同,那么我们称其中一个数为另一个数的相反数,也称这两个数互为相反数.
用字母表示如下:
若a+b=0,则a与b互为相反数.
字母可以表示数学概念.
【例3】绝对值用字母如何表示?倒数呢?
总结
用字母表示数有哪些应用?
课堂练习
1.每包书有12册,n包书有______册.
2.温度由t℃下降2℃后是______℃.
3.明明用t秒走了s米,他的速度为_____米/秒.
4.长方形的长一边长为a,另一边长为1,则其面积为_____.
12n
(t-2)
a
5.下列用字母表示数的书写中规范的是( )
D
甲地到乙地的路程
课堂小结
用字母表示数的意义
利用字母表示数,能把数和数量关系一般化地、简明地表示出来.
用字母表示数的应用
利用字母可以表示:运算律、公式、数量关系、数学概念等.
再见
第4章 代数式
4.1 用字母表示数
运 算 定 律 字 母 表 示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b) +c= a +(b + c)
a×b = b×a
(a×b)×c =a×(b×c)
(a + b) ×c =a×c+b×c
复习旧知
你还记得如何用字母表示运算律吗?
探究新知
1只青蛙,1张嘴,2只眼睛,4条腿,1声扑通跳下水;
2只青蛙,2张嘴,4只眼睛,8条腿,2声扑通跳下水.
......
根据此儿歌:
(1)如果青蛙有10只,100只,500只,那么这首儿歌该怎么唱?
(2)如果青蛙的只数用字母n表示,那么这首儿歌又该怎么唱?
解:(1)把青蛙的只数一般化地用字母表示,找出嘴、眼睛、腿、入水响声与只数的关系,代入儿歌即可.
(2)n只青蛙n张嘴,2×n只眼睛,4×n条腿,n声扑通跳下水.
字母可以表示数量关系.
【例1】今日菜市场上的萝卜每千克a元,白菜每千克b元.某食堂要买30kg萝卜,50kg白菜,怎样表示今日要买的萝卜、白菜的总价?
解:要买的萝卜、白菜的总价=萝卜的数量×萝卜的单价+白菜的数量×白菜的单价,所以要买的萝卜、白菜的总价为(30×a+50×b)元,即(30a+50)b元.
注意书写要求:
1.数和表示数的字母相乘,或字母和字母相乘时,乘号可以不写,或用“·”来代替;
2.数和字母相乘,在省略乘号时,要把数字写在字母的前面;
3.数字因数是1或-1时,“1”通常省略不写;
4.带分数和字母相乘时,要把带分数化为假分数;
5.含有字母的除法写成分数的形式.
6.式子后面有单位且式子是和或差的形式时,把式子用括号括起来.
a
a
a
b
a
h
a
h
a
h
b
S = a2
S = ab
S = ah
S = ah÷2
S =(a + b)h÷2
观察下列图形,计算它们的面积,你发现了什么?
字母可以表示公式.
【例2】(1)长方形的长是a米,宽是3米,则面积是多少平方米?周长是多少米?
(2)下面表述中,字母表示什么?①圆的面积是πr2;②正方形的周长是4a.
解:(1)长方形的面积是3a平方米,周长是(a+3)×2米,即(2a+6)米.
(2)①r表示圆的半径;②a表示正方形的边长.
你还记得相反数的定义吗?你能用字母表示互为相反数的两数之间的关系吗?
解:相反数的定义:如果两个数只有符号不同,那么我们称其中一个数为另一个数的相反数,也称这两个数互为相反数.
用字母表示如下:
若a+b=0,则a与b互为相反数.
字母可以表示数学概念.
【例3】绝对值用字母如何表示?倒数呢?
总结
用字母表示数有哪些应用?
课堂练习
1.每包书有12册,n包书有______册.
2.温度由t℃下降2℃后是______℃.
3.明明用t秒走了s米,他的速度为_____米/秒.
4.长方形的长一边长为a,另一边长为1,则其面积为_____.
12n
(t-2)
a
5.下列用字母表示数的书写中规范的是( )
D
甲地到乙地的路程
课堂小结
用字母表示数的意义
利用字母表示数,能把数和数量关系一般化地、简明地表示出来.
用字母表示数的应用
利用字母可以表示:运算律、公式、数量关系、数学概念等.
再见
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
