浙教版数学七年级上册 3.1 平方根 课件(共18张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 3.1 平方根 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 430.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 06:45:43 | ||
图片预览




文档简介
(共18张PPT)
第3章 实数
3.1 平方根
新课导入
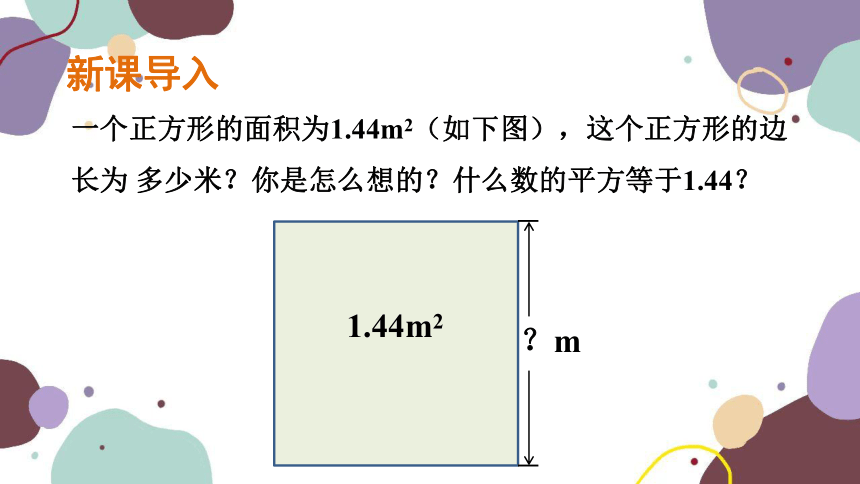
一个正方形的面积为1.44m2(如下图),这个正方形的边长为 多少米?你是怎么想的?什么数的平方等于1.44?
1.44m2
?m
平方根的概念:
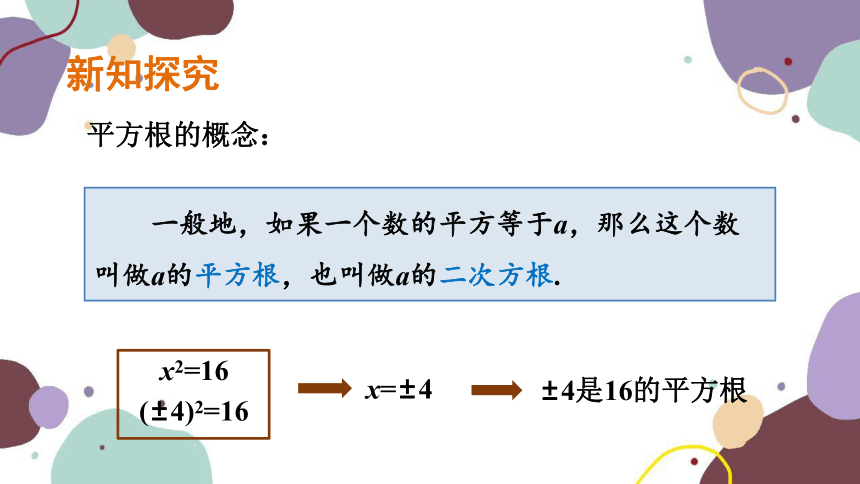
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做a的二次方根.
新知探究
x2=16
x=±4
±4是16的平方根
(±4)2=16
±6
±0
一个正数有正、负两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
平方根的表示方法
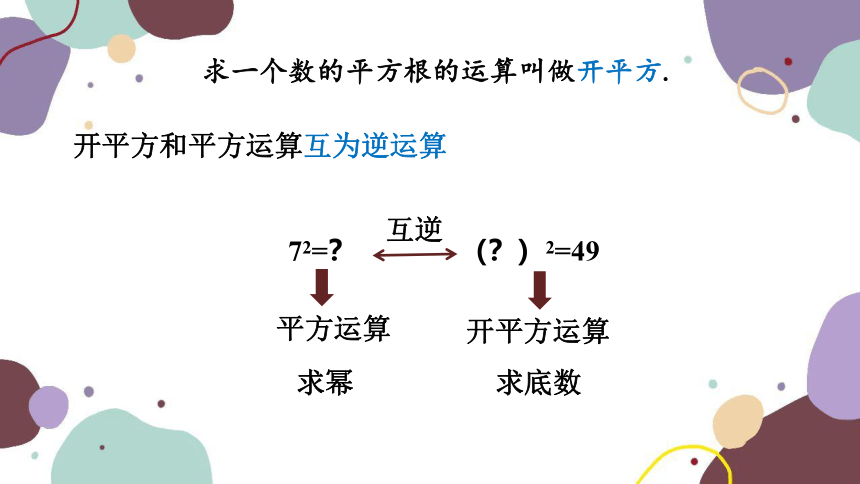
求一个数的平方根的运算叫做开平方.
72=?
平方运算
(?)2=49
开平方运算
互逆
开平方和平方运算互为逆运算
求幂
求底数
算术平方根的性质
算术平方根小数点移动法则
被开方数的小数点每向右(或向左)移动两位,它的算术平方根的小数点就向右(或向左)移动一位.
典型例题
A
分析:
①
②
③
④
不正确
不正确
(-2)2=4,
4平方的根是±2.
正确
2是4的平方根,-2也是4的平方根.
不正确
4平方的根是±2.
【例题2】填空:
①平方根等于它本身的数是_______;
②平方根与算术平方根相等的数是______;
③算术平方根等于它本身的数是_________;
④平方根的平方等于它本身的数是__________;
分析:
0的平方根是0;
①
②
0
0
0和1
非负数
0的平方根是0,0的算术平方根是0;
解:
∵被求式是在两个整数之间,
【例题4】已知一个正数的平方根是2m+1和5-3m,求m的值和这个正数.
解:
∴m的值是6,这个正数是169.
∴2m+1+5-3m=0
∴m=6,
∴2m+1=13,5-3m=-13.
而(±13)2=169.
解:
∴ x+2=0,y-2=0,
∴ x=-2,y=2
课堂练习
1.下列说法正确的是( )
A.任何数的平方根都有两个
B.一个正数的平方根的平方就是这个数
C.负数也有平方根
D.非负数的平方根都有两个
B
分析:一个正数有正、负两个平方根;0的平方根只有0;任何数的平方都为非负数,故负数没有平方根,故A、 C 、D不正确.
2.若a是b(b﹥0)的一个平方根,则b的平方根是( )
A.a B.-a C.±a D.a2
C
3.算术平方根等于它本身的数是________;______的算术平方根等于它的相反数.
0和1
0
A
=7+5-15
=-3.
=4.2.
课堂小结
如果一个数的平方等于a,那么这个数叫做a的平方根(或二次方根).
求一个数a的平方根的运算叫做开平方.
正数的正平方根称为算数平方根.
一个正数有正、负两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
再见
第3章 实数
3.1 平方根
新课导入
一个正方形的面积为1.44m2(如下图),这个正方形的边长为 多少米?你是怎么想的?什么数的平方等于1.44?
1.44m2
?m
平方根的概念:
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也叫做a的二次方根.
新知探究
x2=16
x=±4
±4是16的平方根
(±4)2=16
±6
±0
一个正数有正、负两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
平方根的表示方法
求一个数的平方根的运算叫做开平方.
72=?
平方运算
(?)2=49
开平方运算
互逆
开平方和平方运算互为逆运算
求幂
求底数
算术平方根的性质
算术平方根小数点移动法则
被开方数的小数点每向右(或向左)移动两位,它的算术平方根的小数点就向右(或向左)移动一位.
典型例题
A
分析:
①
②
③
④
不正确
不正确
(-2)2=4,
4平方的根是±2.
正确
2是4的平方根,-2也是4的平方根.
不正确
4平方的根是±2.
【例题2】填空:
①平方根等于它本身的数是_______;
②平方根与算术平方根相等的数是______;
③算术平方根等于它本身的数是_________;
④平方根的平方等于它本身的数是__________;
分析:
0的平方根是0;
①
②
0
0
0和1
非负数
0的平方根是0,0的算术平方根是0;
解:
∵被求式是在两个整数之间,
【例题4】已知一个正数的平方根是2m+1和5-3m,求m的值和这个正数.
解:
∴m的值是6,这个正数是169.
∴2m+1+5-3m=0
∴m=6,
∴2m+1=13,5-3m=-13.
而(±13)2=169.
解:
∴ x+2=0,y-2=0,
∴ x=-2,y=2
课堂练习
1.下列说法正确的是( )
A.任何数的平方根都有两个
B.一个正数的平方根的平方就是这个数
C.负数也有平方根
D.非负数的平方根都有两个
B
分析:一个正数有正、负两个平方根;0的平方根只有0;任何数的平方都为非负数,故负数没有平方根,故A、 C 、D不正确.
2.若a是b(b﹥0)的一个平方根,则b的平方根是( )
A.a B.-a C.±a D.a2
C
3.算术平方根等于它本身的数是________;______的算术平方根等于它的相反数.
0和1
0
A
=7+5-15
=-3.
=4.2.
课堂小结
如果一个数的平方等于a,那么这个数叫做a的平方根(或二次方根).
求一个数a的平方根的运算叫做开平方.
正数的正平方根称为算数平方根.
一个正数有正、负两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
再见
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
