浙教版数学七年级上册 5.3.1 合并同类项和去括号课件(共28张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 5.3.1 合并同类项和去括号课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 455.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-07 18:46:03 | ||
图片预览








文档简介
(共28张PPT)
第5章 一元一次方程
5.3 一元一次方程的解法
第1课时 合并同类项和去括号
1.进一步熟悉利用等式的基本性质解一元一次方程的基本过程.
2.通过具体实例归纳出移项法则,会用移项法则解一元一次方程.
3.会解含有括号的一元一次方程,掌握解方程时每一步的变形依据.
2.进一步体会解方程是解决实际问题的重要环节.
教学目标
解方程 :5x-2=8.
解:方程两边都加上2,得
5x-2+2=8+2,
也就是 5x=8+2,
即 5x=10,
解得 x=2.
思考:你能找到比这更简便的解题方法吗?
复习导入
一、移项法则
利用等式的基本性质,我们对两个方程进行了如下变换,观察并回答:
5x -2 = 8
5x = 8 + 2
(1)与原方程相比,哪些项的位置发生了改变?哪些没变?
(2)改变位置的项的符号是否发生了变化?没改变位置的项的符号是否发生了变化?
合作探究
总结归纳
把原方程中的某一项改变________后,从________的一边移到________,这种变形叫做移项.
(1)移项的根据是等式的基本性质1.
(2)移项要变号,没有移动的项不改变符号.
(3)通常把含有未知数的项移到方程的左边,把常数项(不含未知数的项)移到方程的右边.
【移项要点】
符号
方程
另一边
二、利用移项、合并同类项解方程
解下列方程:
(1)2x+6=1 (2)3x+3=2x+7
(2)移项,得 3x-2x=7-3.
合并同类项,得 x=4.
解:(1)
你能总结出利用移项法则解方程的步骤吗?
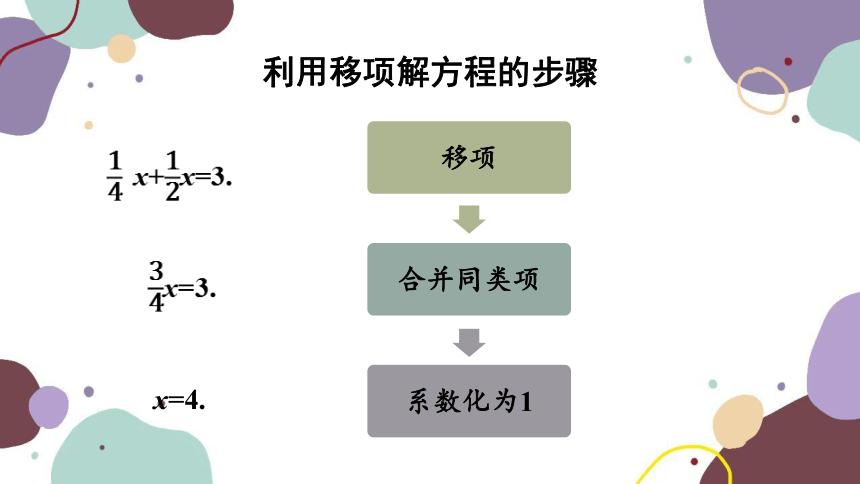
利用移项解方程的步骤
移项
合并同类项
系数化为1
x=4.
【例】 通过移项将下列方程变形,正确的是( )
A.由5x-7=2,得5x=2-7
B.由6x-3=x+4,得3-6x=4+x
C.由8-x=x-5,得-x-x=-5-8
D.由x+9=3x-1,得3x-x=-1+9
C
典例剖析
【解析】A中由5x-7=2,得5x=2+7,故选项A错误;
B中由6x-3=x+4,得6x-x=3+4,故选项B错误;
C中由8-x=x-5,得-x-x=-5-8,故选项C正确;
D中由x+9=3x-1,得3x-x=9+1,故选项D错误.
故选C.
易错点
1.移项时必须是从等号的一边到另一边,并且不要忘记对移动的项变号,如从3+5x=12得到5x=12+3是不对的.
2.没移项时不要误认为移项,如从-9=x得到x=-9,利用的是等式的基本性质(对称性).两者要区分清楚.
4(x+0.5)+x=10-3,
去括号,得
移项,得 4x+x=7-2,
4x+2+x=7,
合并同类项,得 5x=5,
方程两边同除以5,得x=1.
答:1听果奶饮料1元.
三、去括号法则
怎么解这个有括号的方程呢?
总结归纳
通过以上解方程的过程,你能总结出解含有括号一元一次方程的一般步骤吗?
去括号
移项
合并同类项
系数化为1
【例】解方程:-2(x-1)=4.
解:去括号,得 -2x+2=4.
移项,得 -2x=4-2.
合并同类项,得 -2x=2.
系数化为1,得 x=-1.
比较上面两种解法,说说它们的区别.
你还有不同的解法吗?
提示:将x-1看作一个整体
解法二:方程两边同除以-2,得
x-1=-2.
移项,得 x=-2+1.
即 x=-1.
典例剖析
灵活应用
解下列方程:
(1)-x-4=3x; (2)5x-1=9;
解:(1)移项,得 -x-3x=4,
合并同类项,得 -4x=4,
系数化成1,得 x=-1;
(2)移项,得 5x=9+1,
合并同类项,得 5x=10,
系数化成1,得 x=2;
用合并同类项的方法解方程
解下列方程:
(1)4x-3(5-x)=6; (2)5(x+8)-5=6(2x-7).
用去括号的方法解方程
解:(1)去括号,得 4x-15+3x=6,
移项、合并同类项,得 7x=21,
系数化为1,得 x=3.
(2)去括号,得 5x+40-5=12x-42,
移项、合并同类项,得 -7x=-77,
系数化为1,得 x=11.
利用去括号解方程要注意什么?
(1)如果括号外的因数是负数时,去括号后,原括号内各项的符号要改变;
(2)乘数与括号内多项式相乘时,乘数应乘括号内的每一项,
不要漏乘.
去括号必须注意的事项
某羽毛球协会组织一些会员到现场观看某场比赛.已知该协会购买了每张300元和每张400元的两种门票共8张,总费用为2700元.请问该协会购买了这两种门票各多少张?
去括号解方程的应用题
【解析】设每张300元的门票买了x张,则每张400元的门票买了(8-x)张,根据题意建立方程,求出方程的解就可以得出结论.
解:设每张300元的门票买了x张,
则每张400元的门票买了(8-x)张,
由题意得300x+400×(8-x)=2700,
解得x=5,
所以买400元每张的门票张数为8-5=3(张).
答:每张300元的门票买了5张,每张400元的门票买了3张.
A
1.对于方程-3x-7=12x+6,下列移项正确的是( )
A. -3x-12x=6+7
B.-3x+12x= -7+6
C. -3x-12x=7-6
D.12x-3x=6+7
巩固练习
2.在解方程3(x-1)-2(2x+3)=6时,去括号正确的是( )
A. 3x-1-4x+3=6 B. 3x-3-4x-6=6
C. 3x+1-4x-3=6 D. 3x-1+4x-6=6
3.方程4(a-x)-4(x+1)=60的解是x=-1,则a的值是( )
A.-14 B.20 C. 14 D.-16
B
C
4.解下列方程:
(1)-2x+5=-3; (2)10x-2=6x+1+3x.
解:(1)移项,得 -2x=-3-5,
合并同类项,得 -2x=-8,
系数化成1,得 x=4;
(2)移项,得 10x-6x-3x=1+2,
合并同类项,得 x=3.
解:(3)去括号,得 2x-6=5x,
移项,得 2x-5x=6.
合并同类项,得 -3x=6.
系数化为1,得 x=-2.
(3)2(x-3)=5x; (4)4x+3(2x-3)=12-(x+4).
5.一架飞机在两城之间航行,风速为24 km/h,顺风飞行要2小时50分,逆风飞行要3小时,求两城距离.
分析:顺风速度=飞行速度+风速,
逆风速度=飞行速度-风速,
等量关系:顺风路程=逆风路程,
即顺风速度×顺风时间=逆风速度×逆风时间.
利用移项、合并同类项解一元一次方程
移项法则
利用移项、合并同类项解方程
移项的概念
移项法则
移项
系数化为1
合并同类项
课堂小结
去括号解一元一次方程
去括号注意事项
解含有括号的一元一次方程
移项
④系数化1
合并同类项
去括号
谢谢观看
第5章 一元一次方程
5.3 一元一次方程的解法
第1课时 合并同类项和去括号
1.进一步熟悉利用等式的基本性质解一元一次方程的基本过程.
2.通过具体实例归纳出移项法则,会用移项法则解一元一次方程.
3.会解含有括号的一元一次方程,掌握解方程时每一步的变形依据.
2.进一步体会解方程是解决实际问题的重要环节.
教学目标
解方程 :5x-2=8.
解:方程两边都加上2,得
5x-2+2=8+2,
也就是 5x=8+2,
即 5x=10,
解得 x=2.
思考:你能找到比这更简便的解题方法吗?
复习导入
一、移项法则
利用等式的基本性质,我们对两个方程进行了如下变换,观察并回答:
5x -2 = 8
5x = 8 + 2
(1)与原方程相比,哪些项的位置发生了改变?哪些没变?
(2)改变位置的项的符号是否发生了变化?没改变位置的项的符号是否发生了变化?
合作探究
总结归纳
把原方程中的某一项改变________后,从________的一边移到________,这种变形叫做移项.
(1)移项的根据是等式的基本性质1.
(2)移项要变号,没有移动的项不改变符号.
(3)通常把含有未知数的项移到方程的左边,把常数项(不含未知数的项)移到方程的右边.
【移项要点】
符号
方程
另一边
二、利用移项、合并同类项解方程
解下列方程:
(1)2x+6=1 (2)3x+3=2x+7
(2)移项,得 3x-2x=7-3.
合并同类项,得 x=4.
解:(1)
你能总结出利用移项法则解方程的步骤吗?
利用移项解方程的步骤
移项
合并同类项
系数化为1
x=4.
【例】 通过移项将下列方程变形,正确的是( )
A.由5x-7=2,得5x=2-7
B.由6x-3=x+4,得3-6x=4+x
C.由8-x=x-5,得-x-x=-5-8
D.由x+9=3x-1,得3x-x=-1+9
C
典例剖析
【解析】A中由5x-7=2,得5x=2+7,故选项A错误;
B中由6x-3=x+4,得6x-x=3+4,故选项B错误;
C中由8-x=x-5,得-x-x=-5-8,故选项C正确;
D中由x+9=3x-1,得3x-x=9+1,故选项D错误.
故选C.
易错点
1.移项时必须是从等号的一边到另一边,并且不要忘记对移动的项变号,如从3+5x=12得到5x=12+3是不对的.
2.没移项时不要误认为移项,如从-9=x得到x=-9,利用的是等式的基本性质(对称性).两者要区分清楚.
4(x+0.5)+x=10-3,
去括号,得
移项,得 4x+x=7-2,
4x+2+x=7,
合并同类项,得 5x=5,
方程两边同除以5,得x=1.
答:1听果奶饮料1元.
三、去括号法则
怎么解这个有括号的方程呢?
总结归纳
通过以上解方程的过程,你能总结出解含有括号一元一次方程的一般步骤吗?
去括号
移项
合并同类项
系数化为1
【例】解方程:-2(x-1)=4.
解:去括号,得 -2x+2=4.
移项,得 -2x=4-2.
合并同类项,得 -2x=2.
系数化为1,得 x=-1.
比较上面两种解法,说说它们的区别.
你还有不同的解法吗?
提示:将x-1看作一个整体
解法二:方程两边同除以-2,得
x-1=-2.
移项,得 x=-2+1.
即 x=-1.
典例剖析
灵活应用
解下列方程:
(1)-x-4=3x; (2)5x-1=9;
解:(1)移项,得 -x-3x=4,
合并同类项,得 -4x=4,
系数化成1,得 x=-1;
(2)移项,得 5x=9+1,
合并同类项,得 5x=10,
系数化成1,得 x=2;
用合并同类项的方法解方程
解下列方程:
(1)4x-3(5-x)=6; (2)5(x+8)-5=6(2x-7).
用去括号的方法解方程
解:(1)去括号,得 4x-15+3x=6,
移项、合并同类项,得 7x=21,
系数化为1,得 x=3.
(2)去括号,得 5x+40-5=12x-42,
移项、合并同类项,得 -7x=-77,
系数化为1,得 x=11.
利用去括号解方程要注意什么?
(1)如果括号外的因数是负数时,去括号后,原括号内各项的符号要改变;
(2)乘数与括号内多项式相乘时,乘数应乘括号内的每一项,
不要漏乘.
去括号必须注意的事项
某羽毛球协会组织一些会员到现场观看某场比赛.已知该协会购买了每张300元和每张400元的两种门票共8张,总费用为2700元.请问该协会购买了这两种门票各多少张?
去括号解方程的应用题
【解析】设每张300元的门票买了x张,则每张400元的门票买了(8-x)张,根据题意建立方程,求出方程的解就可以得出结论.
解:设每张300元的门票买了x张,
则每张400元的门票买了(8-x)张,
由题意得300x+400×(8-x)=2700,
解得x=5,
所以买400元每张的门票张数为8-5=3(张).
答:每张300元的门票买了5张,每张400元的门票买了3张.
A
1.对于方程-3x-7=12x+6,下列移项正确的是( )
A. -3x-12x=6+7
B.-3x+12x= -7+6
C. -3x-12x=7-6
D.12x-3x=6+7
巩固练习
2.在解方程3(x-1)-2(2x+3)=6时,去括号正确的是( )
A. 3x-1-4x+3=6 B. 3x-3-4x-6=6
C. 3x+1-4x-3=6 D. 3x-1+4x-6=6
3.方程4(a-x)-4(x+1)=60的解是x=-1,则a的值是( )
A.-14 B.20 C. 14 D.-16
B
C
4.解下列方程:
(1)-2x+5=-3; (2)10x-2=6x+1+3x.
解:(1)移项,得 -2x=-3-5,
合并同类项,得 -2x=-8,
系数化成1,得 x=4;
(2)移项,得 10x-6x-3x=1+2,
合并同类项,得 x=3.
解:(3)去括号,得 2x-6=5x,
移项,得 2x-5x=6.
合并同类项,得 -3x=6.
系数化为1,得 x=-2.
(3)2(x-3)=5x; (4)4x+3(2x-3)=12-(x+4).
5.一架飞机在两城之间航行,风速为24 km/h,顺风飞行要2小时50分,逆风飞行要3小时,求两城距离.
分析:顺风速度=飞行速度+风速,
逆风速度=飞行速度-风速,
等量关系:顺风路程=逆风路程,
即顺风速度×顺风时间=逆风速度×逆风时间.
利用移项、合并同类项解一元一次方程
移项法则
利用移项、合并同类项解方程
移项的概念
移项法则
移项
系数化为1
合并同类项
课堂小结
去括号解一元一次方程
去括号注意事项
解含有括号的一元一次方程
移项
④系数化1
合并同类项
去括号
谢谢观看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
