浙教版数学七年级上册 6.7 角的和差 课件(共16张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 6.7 角的和差 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 418.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
第6章 图形的初步知识
6.7 角的和差
教学目标
1.了解角的和差的概念.
2.会表示两个角的和、差,会在图形中辨认角的和差,会用量角器作两个角的和差.
3.理解角平分线的概念,会用量角器画一个角的平分线.
4.会进行有关角的和、差、倍分的简单计算.
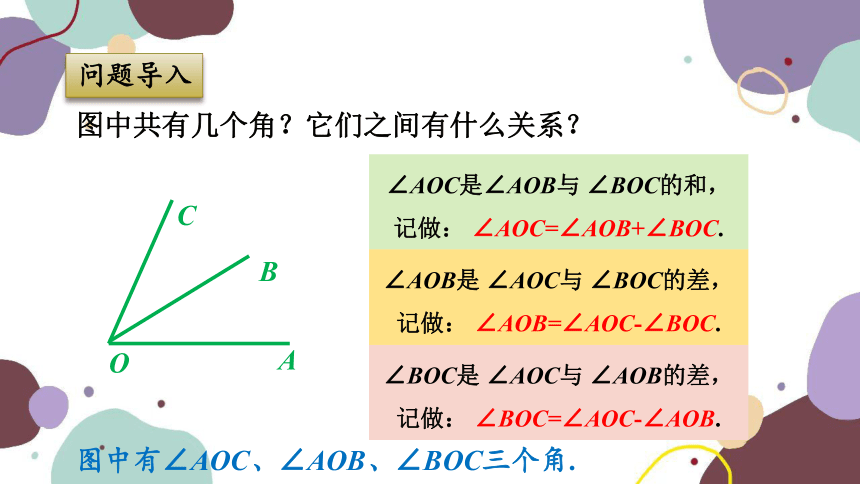
图中共有几个角?它们之间有什么关系?
图中有∠AOC、∠AOB、∠BOC三个角.
问题导入
O
A
C
B
∠BOC是 ∠AOC与 ∠AOB的差,
记做: ∠BOC=∠AOC-∠AOB.
∠AOC是∠AOB与 ∠BOC的和,
记做: ∠AOC=∠AOB+∠BOC.
∠AOB是 ∠AOC与 ∠BOC的差,
记做: ∠AOB=∠AOC-∠BOC.
探究新知
一、角的和差
如果一个角的度数是另两个角的度数的和,那么这个角就叫做另两个角的和;
如果一个角的度数是另两个角的度数的差,那么这个角就叫做另两个角的差;
注意:两个角的和或差仍一个角.
1.∠AOC是哪两个角的和?
2.∠AOB是哪两个角的差?
3.如果∠AOB=∠COD,则 ∠AOC 与∠BOD的大小关系如何?
∠AOC=∠BOD
O
A
C
B
D
∠AOC=∠AOB+∠BOC
∠AOB=∠AOC-∠BOC
或∠AOB= ∠AOD-∠BOD
典例剖析
【例】
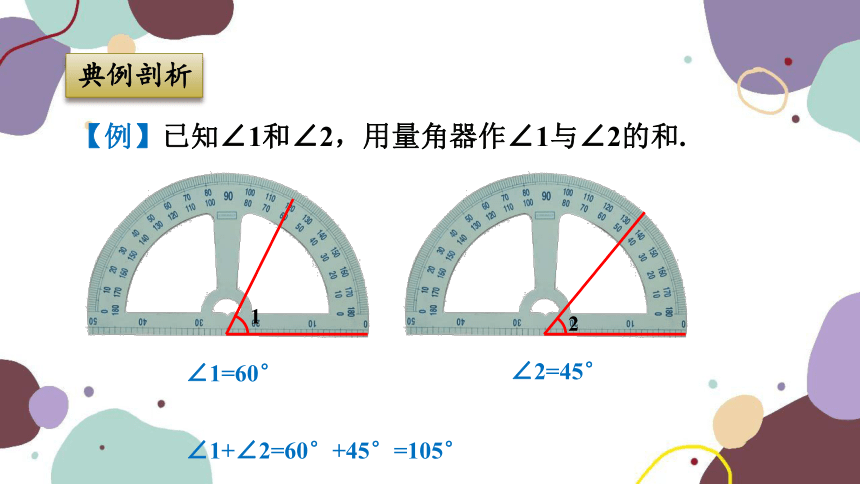
【例】已知∠1和∠2,用量角器作∠1与∠2的和.
典例剖析
1
2
∠1=60°
∠2=45°
∠1+∠2=60°+45°=105°
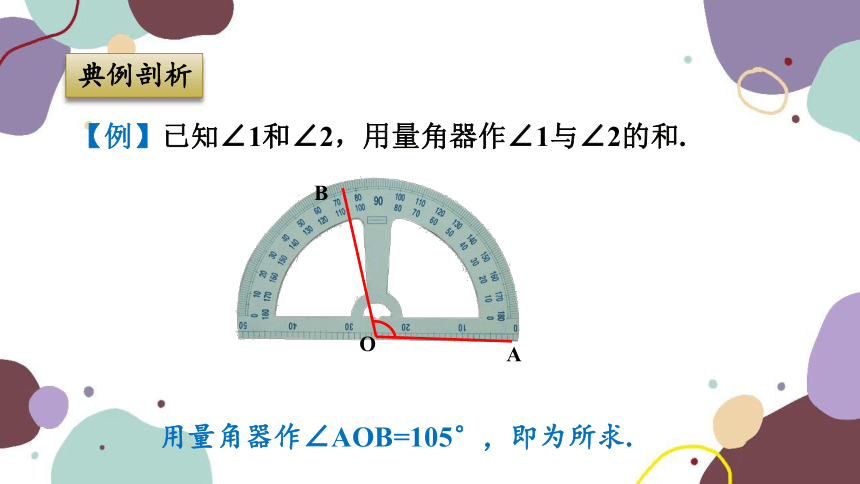
【例】已知∠1和∠2,用量角器作∠1与∠2的和.
典例剖析
A
B
O
用量角器作∠AOB=105°,即为所求.
A
O B
二、角平分线
思考:大家在练习本上画一个角,然后把角的两边对折,展开以后你会发现折痕把角分成了两个角,这两个角有什么关系呢,它们又和原来的角有着怎样的等量关系?
C
这两个角大小相等,
它们是原来角的一半.
【定义】从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.如右下图射线OC.
O
B
A
C
【几何语言】
【类型一】:利用角平分线进行角度的计算
【例】如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1)求∠EOD的度数;
(2)若∠BOC=90°,求∠AOE的度数.
典例剖析
【例】如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1)求∠EOD的度数;
(2)若∠BOC=90°,求∠AOE的度数.
【例】如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1)求∠EOD的度数;
(2)若∠BOC=90°,求∠AOE的度数.
【类型二】:利用三角板叠合进行角度的计算
【例】 如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB=( )
A.120° B.180° C.150° D.135°
B
【解析】由图可得:∠AOC+∠DOB=∠AOB+∠COD=90°+90°=180°.故选B.
典例剖析
【类型三】:角度的计算
【例】计算:
(1)153°29′42″+26°40′32″;
(2)110°36′-90°37′28″;
(3)62°24′17″×4.
解:(1)153°29′42″+26°40′32″=179°69′74″=180°10′14″;
(2)110°36′-90°37′28″=109°95′60″-90°37′28″=19°58′32″;
(3)62°24′17″×4=248°96′68″=249°37′8″.
典例剖析
课堂小结
如果一个角的度数是另两个角的度数的和,那么这个角就叫做另两个角的和;
如果一个角的度数是另两个角的度数的差,那么这个角就叫做另两个角的差;
从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角平分线
角的和差
谢谢观看
第6章 图形的初步知识
6.7 角的和差
教学目标
1.了解角的和差的概念.
2.会表示两个角的和、差,会在图形中辨认角的和差,会用量角器作两个角的和差.
3.理解角平分线的概念,会用量角器画一个角的平分线.
4.会进行有关角的和、差、倍分的简单计算.
图中共有几个角?它们之间有什么关系?
图中有∠AOC、∠AOB、∠BOC三个角.
问题导入
O
A
C
B
∠BOC是 ∠AOC与 ∠AOB的差,
记做: ∠BOC=∠AOC-∠AOB.
∠AOC是∠AOB与 ∠BOC的和,
记做: ∠AOC=∠AOB+∠BOC.
∠AOB是 ∠AOC与 ∠BOC的差,
记做: ∠AOB=∠AOC-∠BOC.
探究新知
一、角的和差
如果一个角的度数是另两个角的度数的和,那么这个角就叫做另两个角的和;
如果一个角的度数是另两个角的度数的差,那么这个角就叫做另两个角的差;
注意:两个角的和或差仍一个角.
1.∠AOC是哪两个角的和?
2.∠AOB是哪两个角的差?
3.如果∠AOB=∠COD,则 ∠AOC 与∠BOD的大小关系如何?
∠AOC=∠BOD
O
A
C
B
D
∠AOC=∠AOB+∠BOC
∠AOB=∠AOC-∠BOC
或∠AOB= ∠AOD-∠BOD
典例剖析
【例】
【例】已知∠1和∠2,用量角器作∠1与∠2的和.
典例剖析
1
2
∠1=60°
∠2=45°
∠1+∠2=60°+45°=105°
【例】已知∠1和∠2,用量角器作∠1与∠2的和.
典例剖析
A
B
O
用量角器作∠AOB=105°,即为所求.
A
O B
二、角平分线
思考:大家在练习本上画一个角,然后把角的两边对折,展开以后你会发现折痕把角分成了两个角,这两个角有什么关系呢,它们又和原来的角有着怎样的等量关系?
C
这两个角大小相等,
它们是原来角的一半.
【定义】从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.如右下图射线OC.
O
B
A
C
【几何语言】
【类型一】:利用角平分线进行角度的计算
【例】如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1)求∠EOD的度数;
(2)若∠BOC=90°,求∠AOE的度数.
典例剖析
【例】如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1)求∠EOD的度数;
(2)若∠BOC=90°,求∠AOE的度数.
【例】如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1)求∠EOD的度数;
(2)若∠BOC=90°,求∠AOE的度数.
【类型二】:利用三角板叠合进行角度的计算
【例】 如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB=( )
A.120° B.180° C.150° D.135°
B
【解析】由图可得:∠AOC+∠DOB=∠AOB+∠COD=90°+90°=180°.故选B.
典例剖析
【类型三】:角度的计算
【例】计算:
(1)153°29′42″+26°40′32″;
(2)110°36′-90°37′28″;
(3)62°24′17″×4.
解:(1)153°29′42″+26°40′32″=179°69′74″=180°10′14″;
(2)110°36′-90°37′28″=109°95′60″-90°37′28″=19°58′32″;
(3)62°24′17″×4=248°96′68″=249°37′8″.
典例剖析
课堂小结
如果一个角的度数是另两个角的度数的和,那么这个角就叫做另两个角的和;
如果一个角的度数是另两个角的度数的差,那么这个角就叫做另两个角的差;
从一个角的顶点出发的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.
角平分线
角的和差
谢谢观看
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
