第2章简单事件的概率复习课
图片预览







文档简介
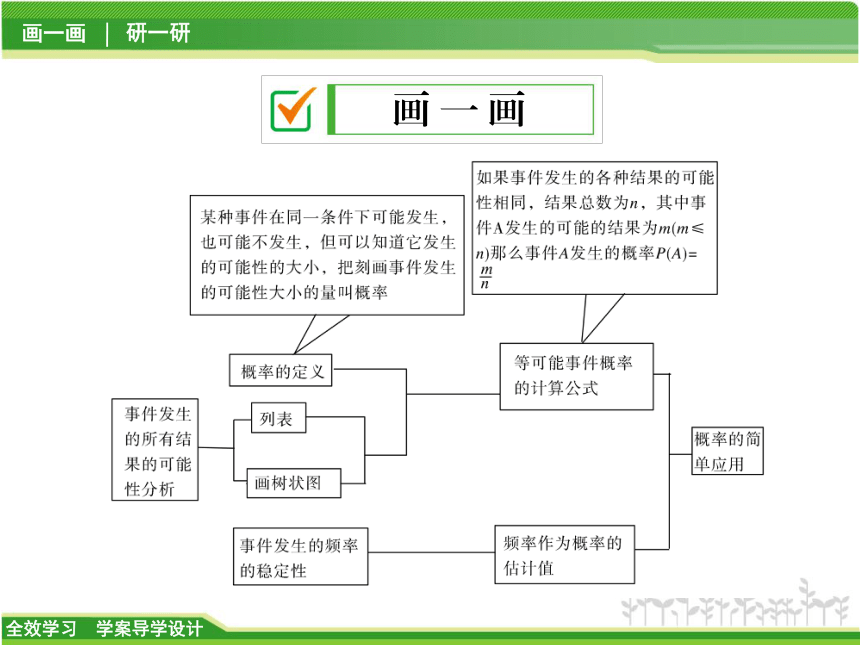
课件38张PPT。第2章 简单事件的概率章末复习课画 一 画研 一 研类型之一 概率的意义
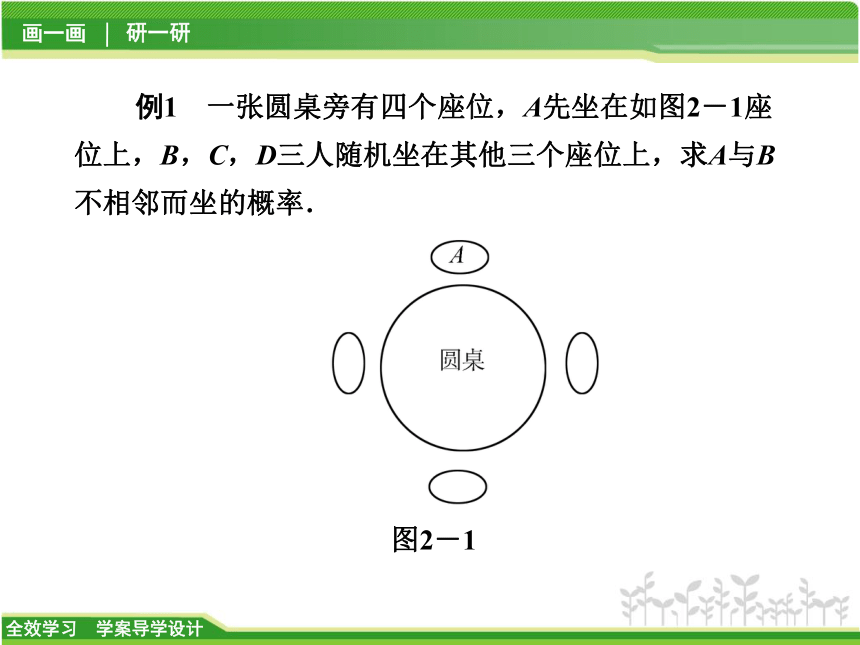
例1 一张圆桌旁有四个座位,A先坐在如图2-1座位上,B,C,D三人随机坐在其他三个座位上,求A与B不相邻而坐的概率.图2-1【解析】 按照题意画出各种情况示意图,再计算A与B不相邻的概率.
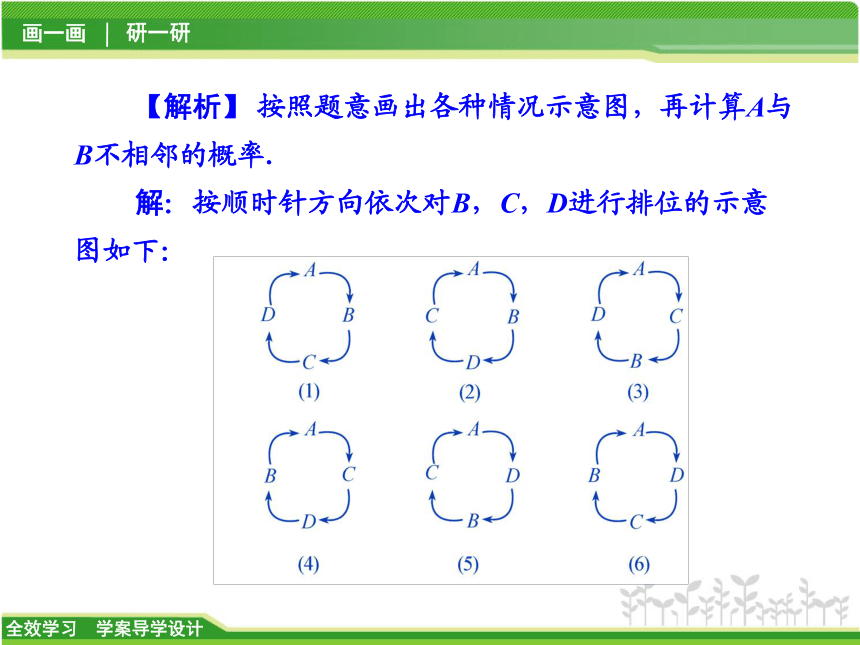
解:按顺时针方向依次对B,C,D进行排位的示意图如下: 一口袋中装有四根长度分别为1 cm,3 cm,4 cm和5 cm的细木棒,小明手中有一根长度为3 cm的细木棒,现随机从袋内取出两根细木棒与小明手中的细木棒放在一起,回答下列问题:
(1)求这三根细木棒能构成三角形的概率;
(2)求这三根细木棒能构成直角三角形的概率;
(3)求这三根细木棒能构成等腰三角形的概率.
解: 用枚举法或列表法,可求出从四根细木棒中取两根细木棒的所有可能情况共有6种.枚举法:(1,3),(1,4),(1,5),(3,4),(3,5),(4,5).类型之二 用列表法或树状图求概率
求等可能事件发生的概率常用列表法来分析事件发生的结果,当一次试验要涉及两个因素并且可能出现的结果数目较多时,为了不重不漏地列出所有可能的结果,则用列表法.
用树状图列举的结果看起来一目了然,当事件要经过多次步骤(三步以上)完成时,用树状图的方法求事件的概率很有效.例2 有两个可以自由转动的均匀转盘A,B都被分成了3等份,并在每一份内均标有数字,如图2-2所示,规则如下:
①分别转动转盘A,B;②两个转盘停止后观察两个指针所指份内的数字(若指针停在分界线上,那么重转一次,直到指针指向某一份内为止).
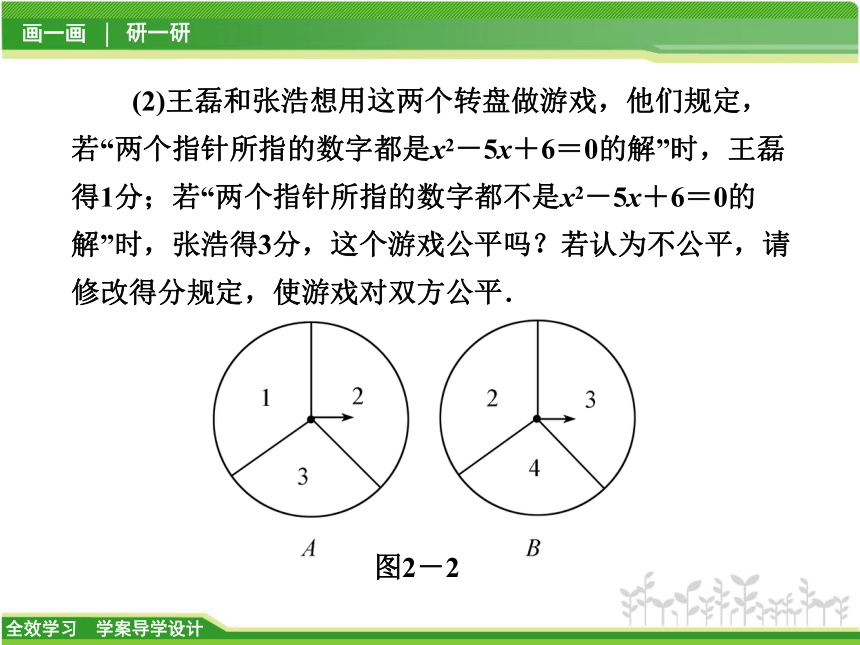
(1)用列表法(或树状图)分别求出“两个指针所指的数字都是方程x2-5x+6=0的解”的概率和“两个指针所指的数字都不是方程x2-5x+6=0的解”的概率;(2)王磊和张浩想用这两个转盘做游戏,他们规定,若“两个指针所指的数字都是x2-5x+6=0的解”时,王磊得1分;若“两个指针所指的数字都不是x2-5x+6=0的解”时,张浩得3分,这个游戏公平吗?若认为不公平,请修改得分规定,使游戏对双方公平.
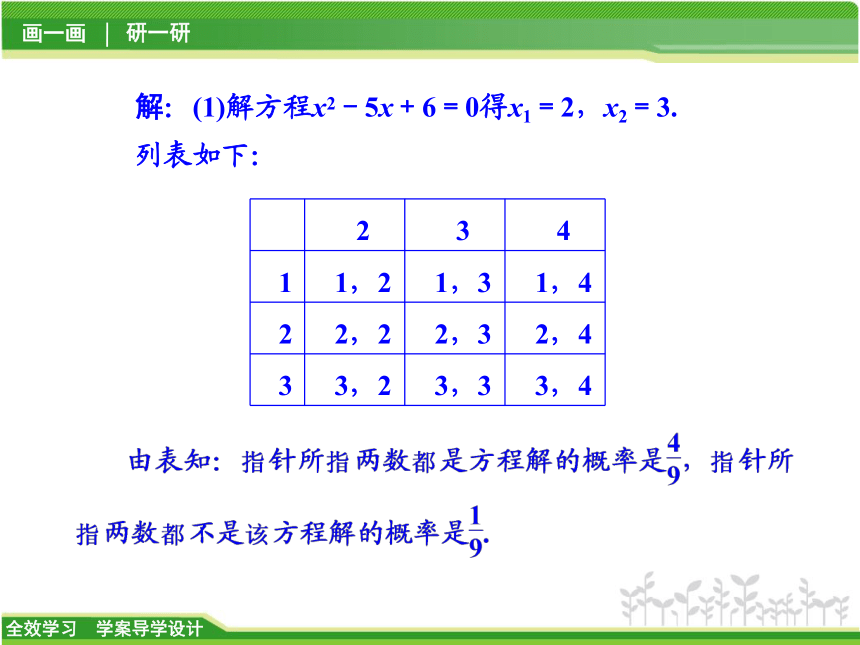
图2-2解:(1)解方程x2-5x+6=0得x1=2,x2=3.
列表如下: 1.如图2-3所示,A,B两个转盘分别被平均分成三个、四个扇形,分别转动A盘、B盘各一次.转动过程中,指针保持不动,如果指针恰好指在分界线上,则重转一次,直到指针指向一个数字所在的区域为止.请用列表或画树状图的方法,求两个转盘停止后指针所指区域内的数字之和小于6的概率.
图2-3解:方法一:画树状图如下:2.如图2-4所示,有两个可以自由转动的均匀转盘,转盘A被分成面积相等的三个扇形,转盘B被分成面积相等的四个扇形,每个扇形内都涂有颜色.同时转动两个转盘,停止转动后,若一个转盘的指针指向红色,另一个转盘的指针指向蓝色,则配成紫色;若指针指向分界线时,需重新转动两个转盘.图2-4(1)用列表或画树状图的方法,求同时转动一次转盘A,B配成紫色的概率;
(2)小强和小丽要用这两个转盘做游戏,他们想出如下两种游戏规则:
①转动两个转盘,停止后配成紫色,小强获胜;否则小丽获胜.
②转动两个转盘,停止后指针都指向红色,小强获胜;指针都指向蓝色,小丽获胜.判断以上两种规则的公平性,并说明理由.解:(1)方法一:用树状图表示所有可能出现的结果:由树状图可知,转盘A,B同时转动一次出现12种等可能的情况,其中有4种可配成紫色,方法二:用列表法表示所有可能出现的结果:类型之三 用频率估计概率
通过大量重复试验,用一个事件发生的频率来估计这一事件发生的概率.(1)求袋中黄球的个数;
(2)第一次摸出一个小球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到的都是红球的概率;(3)若规定摸到红球得5分,摸到黄球得3分,摸到蓝球得1分,小明共摸6次小球(每次摸1个球,摸后放回)得20分,问小明有哪几种摸法.(2)(3)设小明摸到红球有x次,摸到黄球有y次,则摸到蓝球有(6-x-y)次,由题意得5x+3y+(6-x-y)=20,即2x+y=7,∴y=7-2x.∵x,y,6-x-y均为自然数,∴当x=1时,y=5,6-x-y=0;当x=2时,y=3,6-x-y=1;当x=3时,y=1,6-x-y=2.综上:小明共有三种摸法:摸到红、黄、蓝三种球分别为1次、5次、0次或2次、3次、1次或3次、1次、2次.【点悟】 本题考查概率的求法. 一个口袋中放有20个球,其中红球6个,白球和黑球各若干个,每个球除了颜色外没有任何区别.(2)若小王取出的第一个球是白球,将它放在桌上,闭上眼睛从袋中余下的球中再任意取一个球,取出红球的概率是多少?
【解析】 利用频率估计概率,建立方程.类型之四 概率与方程(组)、几何等知识的综合运用
近年来出现了把概率与其他数学知识结合起来考查的新题型,解决这类问题时,要综合运用学科内的各种知识,用列表法或树状图帮助分析,求其概率的大小.
例4 某电脑公司现有A,B,C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1)写出所有选购方案(利用树状图或列表法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?(3)现知希望中学购买甲、乙两种品牌电脑共36台(价格如图2-5所示),恰好用了10万元人民币,其中甲品牌电脑为A型号电脑,求购买的A型号电脑有几台.
图2-5【解析】 这是一个概率和二元一次方程组的综合问题,先用列表法或用树状图求出可能的结果,进而求出概率,再根据包含A的方案列方程组.
解:(1)树状图如下:列表法如下:有6种可能结果:(A,D),(A,E),(B,D),(B,E),(C,D),(C,E). 在一次数学活动中,黑板上画着如图2-6所示的图形,活动前老师在准备的四张纸片上分别写有如下四个等式中的一个等式:图2-6①AB=DC
②∠ABE=∠DCE
③AE=DE
④∠A=∠D
小明同学闭上眼睛从四张纸片中随机抽取一张,再从剩下的纸片中随机抽取另一张.请结合图形解答下列两个问题:
(1)当抽得①和②时,用①②作为条件能判定△BEC是等腰三角形吗?说说你的理由;(2)请你用树状图或列表法表示抽取两张纸片上的等式所有可能出现的结果(用序号表示),并求以已经抽取的两张纸片上的等式为条件,不能使△BEC构成等腰三角形的概率.所有可能出现的结果①②,①③,①④,②①,②③,②④,③①,③②,③④,④①,④②,④③.
也可以用表格表示如下:
例1 一张圆桌旁有四个座位,A先坐在如图2-1座位上,B,C,D三人随机坐在其他三个座位上,求A与B不相邻而坐的概率.图2-1【解析】 按照题意画出各种情况示意图,再计算A与B不相邻的概率.
解:按顺时针方向依次对B,C,D进行排位的示意图如下: 一口袋中装有四根长度分别为1 cm,3 cm,4 cm和5 cm的细木棒,小明手中有一根长度为3 cm的细木棒,现随机从袋内取出两根细木棒与小明手中的细木棒放在一起,回答下列问题:
(1)求这三根细木棒能构成三角形的概率;
(2)求这三根细木棒能构成直角三角形的概率;
(3)求这三根细木棒能构成等腰三角形的概率.
解: 用枚举法或列表法,可求出从四根细木棒中取两根细木棒的所有可能情况共有6种.枚举法:(1,3),(1,4),(1,5),(3,4),(3,5),(4,5).类型之二 用列表法或树状图求概率
求等可能事件发生的概率常用列表法来分析事件发生的结果,当一次试验要涉及两个因素并且可能出现的结果数目较多时,为了不重不漏地列出所有可能的结果,则用列表法.
用树状图列举的结果看起来一目了然,当事件要经过多次步骤(三步以上)完成时,用树状图的方法求事件的概率很有效.例2 有两个可以自由转动的均匀转盘A,B都被分成了3等份,并在每一份内均标有数字,如图2-2所示,规则如下:
①分别转动转盘A,B;②两个转盘停止后观察两个指针所指份内的数字(若指针停在分界线上,那么重转一次,直到指针指向某一份内为止).
(1)用列表法(或树状图)分别求出“两个指针所指的数字都是方程x2-5x+6=0的解”的概率和“两个指针所指的数字都不是方程x2-5x+6=0的解”的概率;(2)王磊和张浩想用这两个转盘做游戏,他们规定,若“两个指针所指的数字都是x2-5x+6=0的解”时,王磊得1分;若“两个指针所指的数字都不是x2-5x+6=0的解”时,张浩得3分,这个游戏公平吗?若认为不公平,请修改得分规定,使游戏对双方公平.
图2-2解:(1)解方程x2-5x+6=0得x1=2,x2=3.
列表如下: 1.如图2-3所示,A,B两个转盘分别被平均分成三个、四个扇形,分别转动A盘、B盘各一次.转动过程中,指针保持不动,如果指针恰好指在分界线上,则重转一次,直到指针指向一个数字所在的区域为止.请用列表或画树状图的方法,求两个转盘停止后指针所指区域内的数字之和小于6的概率.
图2-3解:方法一:画树状图如下:2.如图2-4所示,有两个可以自由转动的均匀转盘,转盘A被分成面积相等的三个扇形,转盘B被分成面积相等的四个扇形,每个扇形内都涂有颜色.同时转动两个转盘,停止转动后,若一个转盘的指针指向红色,另一个转盘的指针指向蓝色,则配成紫色;若指针指向分界线时,需重新转动两个转盘.图2-4(1)用列表或画树状图的方法,求同时转动一次转盘A,B配成紫色的概率;
(2)小强和小丽要用这两个转盘做游戏,他们想出如下两种游戏规则:
①转动两个转盘,停止后配成紫色,小强获胜;否则小丽获胜.
②转动两个转盘,停止后指针都指向红色,小强获胜;指针都指向蓝色,小丽获胜.判断以上两种规则的公平性,并说明理由.解:(1)方法一:用树状图表示所有可能出现的结果:由树状图可知,转盘A,B同时转动一次出现12种等可能的情况,其中有4种可配成紫色,方法二:用列表法表示所有可能出现的结果:类型之三 用频率估计概率
通过大量重复试验,用一个事件发生的频率来估计这一事件发生的概率.(1)求袋中黄球的个数;
(2)第一次摸出一个小球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到的都是红球的概率;(3)若规定摸到红球得5分,摸到黄球得3分,摸到蓝球得1分,小明共摸6次小球(每次摸1个球,摸后放回)得20分,问小明有哪几种摸法.(2)(3)设小明摸到红球有x次,摸到黄球有y次,则摸到蓝球有(6-x-y)次,由题意得5x+3y+(6-x-y)=20,即2x+y=7,∴y=7-2x.∵x,y,6-x-y均为自然数,∴当x=1时,y=5,6-x-y=0;当x=2时,y=3,6-x-y=1;当x=3时,y=1,6-x-y=2.综上:小明共有三种摸法:摸到红、黄、蓝三种球分别为1次、5次、0次或2次、3次、1次或3次、1次、2次.【点悟】 本题考查概率的求法. 一个口袋中放有20个球,其中红球6个,白球和黑球各若干个,每个球除了颜色外没有任何区别.(2)若小王取出的第一个球是白球,将它放在桌上,闭上眼睛从袋中余下的球中再任意取一个球,取出红球的概率是多少?
【解析】 利用频率估计概率,建立方程.类型之四 概率与方程(组)、几何等知识的综合运用
近年来出现了把概率与其他数学知识结合起来考查的新题型,解决这类问题时,要综合运用学科内的各种知识,用列表法或树状图帮助分析,求其概率的大小.
例4 某电脑公司现有A,B,C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1)写出所有选购方案(利用树状图或列表法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?(3)现知希望中学购买甲、乙两种品牌电脑共36台(价格如图2-5所示),恰好用了10万元人民币,其中甲品牌电脑为A型号电脑,求购买的A型号电脑有几台.
图2-5【解析】 这是一个概率和二元一次方程组的综合问题,先用列表法或用树状图求出可能的结果,进而求出概率,再根据包含A的方案列方程组.
解:(1)树状图如下:列表法如下:有6种可能结果:(A,D),(A,E),(B,D),(B,E),(C,D),(C,E). 在一次数学活动中,黑板上画着如图2-6所示的图形,活动前老师在准备的四张纸片上分别写有如下四个等式中的一个等式:图2-6①AB=DC
②∠ABE=∠DCE
③AE=DE
④∠A=∠D
小明同学闭上眼睛从四张纸片中随机抽取一张,再从剩下的纸片中随机抽取另一张.请结合图形解答下列两个问题:
(1)当抽得①和②时,用①②作为条件能判定△BEC是等腰三角形吗?说说你的理由;(2)请你用树状图或列表法表示抽取两张纸片上的等式所有可能出现的结果(用序号表示),并求以已经抽取的两张纸片上的等式为条件,不能使△BEC构成等腰三角形的概率.所有可能出现的结果①②,①③,①④,②①,②③,②④,③①,③②,③④,④①,④②,④③.
也可以用表格表示如下:
同课章节目录
