3.1圆的有关概念

课件30张PPT。第3章 圆的基本性质3.1 圆第1课时 圆的有关概念【学习目标】
1．掌握圆的定义，了解弦、直径、弧、半圆等与圆有关概念；
2．掌握点与圆的位置关系；
3．了解圆中的有关计算．
?【学法指导】
1．从生活中圆的形象加强对圆的定义的理解；
2．对与圆有关概念的理解，是解决相关问题的关键；
3．与半径有关的问题可以想到利用全等或等腰三角形有关知识解决；
4．点和圆的位置关系应抓住点到圆的距离与半径的大小关系.
1．圆的概念
定义1：在同一平面内，线段OP绕它固定的一个端点O_________一周，另一端点P所经过的___________叫做圆，定点O叫做________，线段OP叫做圆的________．以点O为圆心的圆，记作“⊙O”，读做“圆O”．(如图3－1－1所示)【知识管理】填 一 填旋转封闭曲线圆心半径图3－1－1注意：圆是一条封闭曲线，而不是一个圆面．定义2：圆是到一个定点(圆心)的距离等于定长(半径)的点组成的图形．
圆的确定：圆是由圆心和半径确定的，圆心确定圆的位置，半径确定圆的大小．
2．与圆的有关概念
弦与直径：连结圆上任意两点的线段叫做弦．经过圆心的弦叫做直径．
注意：(1)直径是圆中最长的弦．
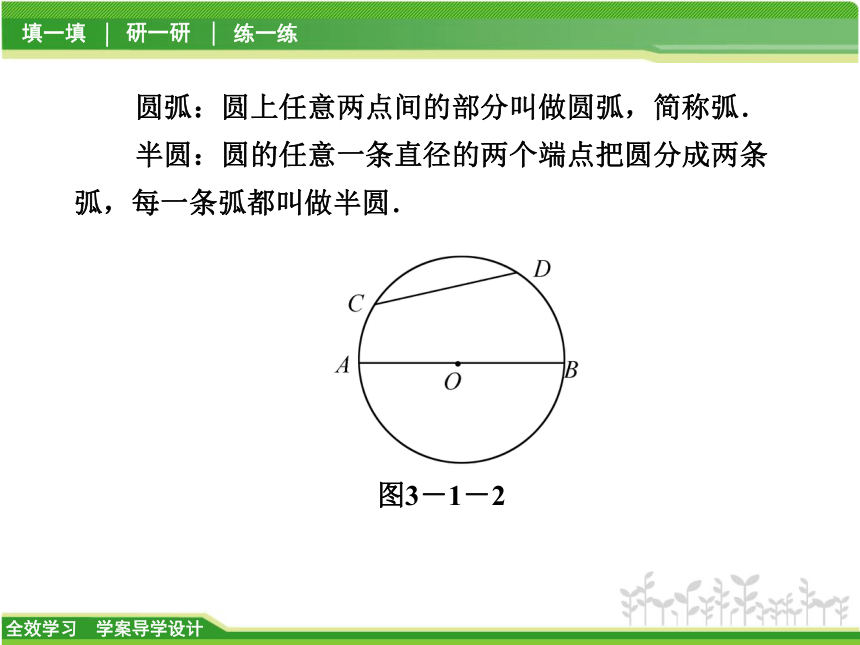
(2)直径是弦，但弦不一定是直径．圆弧：圆上任意两点间的部分叫做圆弧，简称弧．
半圆：圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．图3－1－2注意：半圆是弧，但弧不一定是半圆．等圆：半径相等的两个圆叫做_________．
相等的弧：能够_________的圆弧称为相等的弧．
3．点与圆的位置关系
明确：如果用r表示圆的半径，d表示平面内一点到圆心的距离，则有：
(1)d>r?点在圆______；
(2)d＝r?点在圆_______；
(3)d1．(知识点1)下列语句正确的是 (　 　)
①过圆上一点作圆最长的弦可以作无数条；
②长度相等的弧是等弧；
③圆上的点到圆心的距离都相等；
④同圆或等圆中，优弧一定比劣弧长．
A．①③　　　　　 B．②④
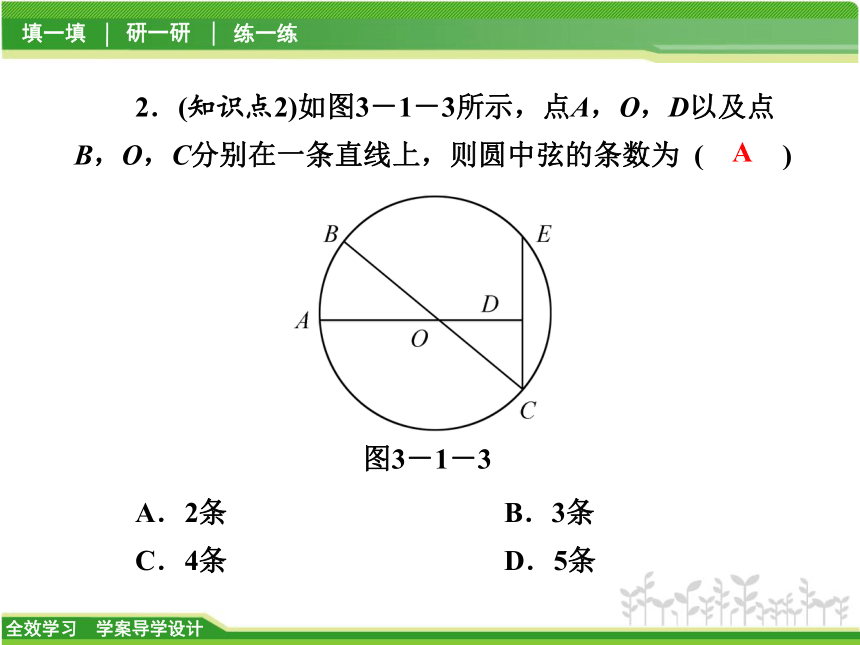
C．②③ D．③④【对点自测】D2．(知识点2)如图3－1－3所示，点A，O，D以及点B，O，C分别在一条直线上，则圆中弦的条数为 (　 　)图3－1－3A．2条 B．3条
C．4条 D．5条A3．(知识点3)若⊙O的半径为4 cm，点A到圆心O的距离为3 cm，那么点A与⊙O的位置关系是 (　 　)
A．点A在圆内 B．点A在圆上
C．点A在圆外 D．不能确定
【解析】 d＝3＜4＝r，所以点A在⊙O内．A4．(知识点3)如图3－1－4所示，已知∠AOB＝60°，则△AOB是_________三角形．图3－1－4等边5．(知识点3)已知⊙O的半径为10 cm，点P到圆心的距离为d cm，
(1)当d＝8 cm时，点P在⊙O______；
(2)当d＝10 cm时，点P在⊙O______；
(3)当d＝12 cm时，点P在⊙O______．
【解析】 d>r?点P在圆外；d＝r?点P在圆上；d例1　下列说法中：
①直径相等的两个圆是等圆；
②长度相同的两条弧是等弧；
③圆中最长的弦是通过圆心的弦；
④一条弦把圆分成两条弧，这两条弧不可能是等弧．
正确的是 (　 　)BA．①②　　　　　　 B．①③
C．②③ D．③④
【解析】 ①直径相等即为半径相等，因此直径相等的两个圆是等圆，故①是正确的；②等弧指能够完全重合的两条弧，即指弧的度数和长度均相等，故②不正确；③正确；④直径把圆分成的两条弧是等弧，所以④是错误的．【点悟】 等弧是指弧的度数和长度均相等的弧，等弧只可能出现在同圆或等圆中． 1.下列说法：
①直径是弦；②弦是直径；③半圆是弧，弧不一定是半圆；④优弧一定大于劣弧；⑤直径是圆中最长的弦．其中正确的说法为 (　 　)
A．①③④ B．①③⑤
C．②③⑤ D．③④⑤
【解析】 其中②，④都是错的，只有在同圆或等圆中优弧一定大于劣弧．B图3－1－5ADACAD类型之二　了解点与圆的位置关系
例2　如图3－1－6所示，在Rt△ABC中，∠C＝90°，BC＝3 cm，AC＝4 cm，以B为圆心，以BC为半径作⊙B，问点A，C及AB，AC的中点D，E与⊙B有怎样的位置关系？图3－1－6【解析】 先求出点A，C，D，E到圆心B的距离，再与半径3 cm进行比较．【点悟】 利用比较半径r与点到圆心的距离d的大小判断点与圆的位置关系． 1.已知⊙O的半径为5 cm，P为⊙O外一点，则OP的长可能是 (　 　)
A．5 cm B．4 cm
C．3 cm D．6 cm
【解析】 ∵点P在⊙O外，∴d>5 cm，故选D.D2．若点P到⊙O的最小距离为4 cm，最大距离为9 cm，则该圆的直径是 (　 　)
A．2.5 cm或6.5 cm B．5 cm
C．13 cm D．5 cm或13 cm
【解析】 分点P在⊙O内和点P在⊙O外两种情形，点P到圆的最大距离和最小距离都需考虑过圆心的直线．
(1)当点P在⊙O内时，如图甲所示，PA为点P到圆的最大距离，PB为点P到圆的最小距离，所以AB＝PA＋PB＝9＋4＝13(cm)；D(2)当点P在⊙O外时，如图乙所示，AB＝PA－PB＝9－4＝5(cm)，所以该圆的直径为13 cm或5 cm，故选D.【点悟】 本题分点P在圆内和圆外两种情况讨论，易忽略其中的一种情形．类型之三　了解圆中的有关计算
例3　如图3－1－7所示，已知CD是⊙O的直径，∠EOD＝78°，AE交⊙O于点B，且AB＝OC，求∠A的度数．图3－1－7【解析】 已知∠EOD＝78°，与未知∠A构成了内、外角关系，而∠OEB也未知，且AB＝OC这一条件不能直接使用，因此想到同圆的半径相等，需连结半径OB，从而得到OB＝AB.
解：连结OB(如图所示)．∵AB＝OC，OB＝OC，
∴AB＝OB，∠A＝∠1，
又∵OB＝OE，∠OEB＝∠2＝∠1＋∠A＝2∠A，
∴∠DOE＝∠OEB＋∠A＝3∠A.
而∠DOE＝78°，
∴3∠A＝78°，∠A＝26°.【点悟】 作圆的半径，利用同圆的半径相等解题是圆中常见的辅助线． 1.如图3－1－8，AB是⊙O的直径，CD是⊙O的弦，AB，CD的延长线交于点E，已知AB＝2DE，若△COD为直角三角形，则∠E的度数为___________.
图3－1－822.5°2．如图3－1－9，AB是⊙O的直径，CD是⊙O的弦，AB，CD的延长线交于点E.已知AB＝2DE，∠AEC＝25°，求∠AOC的度数．图3－1－9解：连结OD，∵AB＝2DE＝2OD，∴OD＝DE，
又∵∠E＝25°，∴∠DOE＝∠E＝25°，∴∠ODC＝50°，同理∠C＝∠ODC＝50°，∴∠AOC＝∠E＋∠OCE＝75°.练 一 练