3.1确定圆的条件
图片预览








文档简介
课件29张PPT。第2课时 确定圆的条件【学习目标】
1.掌握确定圆的条件;
2.理解三角形的外接圆、圆的内接三角形,内心等概念;
3.会确定一个圆的圆心.
【学法指导】
1.对“不在同一直线上的三个点确定一个圆”的理解可以从过一个点的圆、过两个点的圆、过三个点的圆作图来理解;
2.三角形的外接圆有关的计算常与勾股定理、方程思想结合在一起;
3.分类讨论思想在讨论外心的位置时需要用到.填 一 填
1.不在同一直线上的三个点确定一个圆
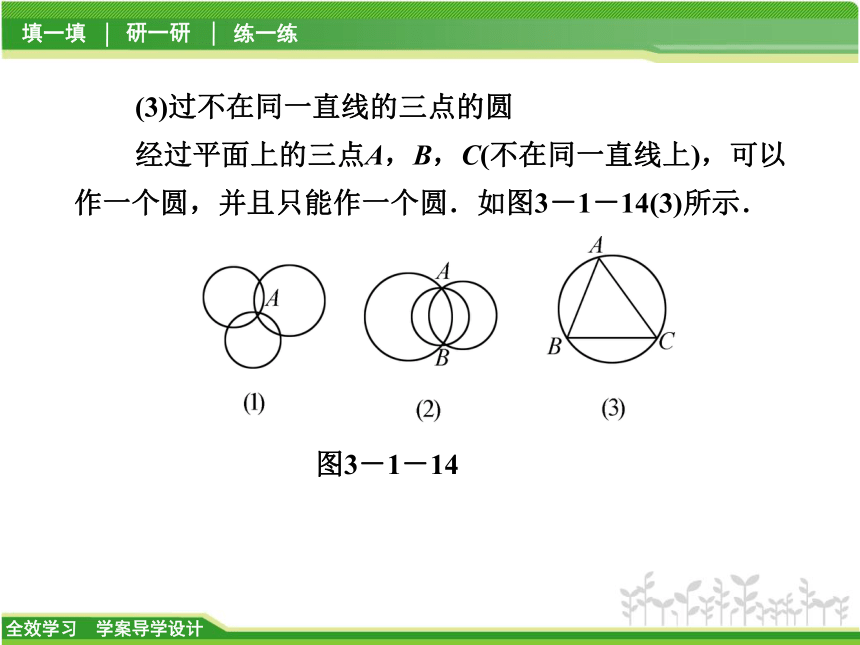
(1)过一点的圆
经过平面上的一点A可以画无数个圆,圆心可以是平面上异于点A的任意一点.如图3-1-14(1)所示.
(2)过两点的圆
经过平面上的两点A,B可以画无数个圆,圆心一定在AB的垂直平分线上.如图3-1-14(2)所示.【知识管理】(3)过不在同一直线的三点的圆
经过平面上的三点A,B,C(不在同一直线上),可以作一个圆,并且只能作一个圆.如图3-1-14(3)所示.
图3-1-142.三角形的外接圆
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.图3-1-15如图3-1-15所示,⊙O经过△ABC的三个顶点A,B,C,那么,⊙O是△ABC的外接圆,点O是△ABC的外心,△ABC是⊙O的内接三角形.
外心:(1)三角形的外心是_______________________ _______的交点.
(2)三角形的外心到三角形____________________相等.
(3)锐角三角形的外心在三角形的_________,直角三角形的外心是____________________,钝角三角形的外心在三角形的________,反之也成立.三角形三条边的垂直平分线三个顶点的距离内部三角形的斜边中点外部
1.(知识点1)已知△ABC,若过点A、点B作圆,那么下面说法正确的是 ( )
A.这样的圆只能作出一个
B.这样的圆只能作出两个
C.点C不在该圆的外部,就在该圆的内部
D.圆心分布在AB的中垂线上【对点自测】D2.(知识点2)三角形的外心是三角形三边的________ ______的交点,它到三角形的___________的距离相等.
3.(知识点2)在△ABC中,∠C=90°,AC=8,BC=6,则△ABC的外接圆直径的长为_______.
4.(知识点1)已知直线a和直线外的两点A,B,经过A,B作一圆,使它的圆心在直线a上.图3-1-16垂直平分线三个顶点10解:作图如下:研 一 研类型之一 三角形的外接圆的有关概念及作图
例1 下列说法正确的是 ( )
A.经过三个点一定可以作圆
B.任意一个圆一定有内接三角形,并且只有一个内接三角形
C.任意一个三角形一定有一个外接圆,并且只有一个外接圆
D.三角形的外心到三角形各边的距离都相等C【解析】 过同一直线上的三点不能作圆,故A不正确;一个圆有无数多个内接三角形,故B不正确;三角形的外心是其三边垂直平分线的交点,所以三角形的外心到三个顶点的距离相等,故D不正确. 1.如图3-1-17,直角坐标系中一条圆弧经过格点A,B,C,其中,B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 ( )
图3-1-17CA.(2,1) B.(2,2)
C.(2,0) D.(2,-1)
【解析】作弦AB和BC的垂直平分线,交点即为圆心.如图所示,则圆心是(2,0).2.某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图3-1-18中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹)图3-1-18解:在圆上取两个弦,作出两弦的垂直平分线即可.类型之二 三角形的外接圆的有关计算
例2 如图3-1-19所示,在△ABC中,AB=AC=10,BC=12,求△ABC的外接圆半径.图3-1-19【解析】 欲求△ABC外接圆的半径,关键找到圆心,由于△ABC是等腰三角形且AB=AC,作出BC边上的高AD,则圆心一定在AD上,设点O为外心,连结OB,在Rt△ODB中可求出半径.
解:过A作AD⊥BC,垂足为D,在AD上取一点O,连结OB,设O为△ABC外接圆圆心,且OA=OB=x.
∵△ABC为等腰三角形,AD⊥BC,【点悟】 构造直角三角形,设出未知数,利用勾股定理建立关于未知数的方程,是解决几何问题中线段长的常用方法. 如图3-1-20,已知△ABC,AB=AC=8,∠BAC=120°,请用圆规和直尺作出△ABC的外接圆.并计算此外接圆的半径.
图3-1-20解:画图如下:
∵AB=AC=8,∠BAC=120°,AO⊥BC,
∴∠BAO=60°,
∴△ABO为等边三角形,
∴△ABC的外接圆的半径为8.
类型之三 证明几个点在同一个圆上
例3 如图3-1-21所示,已知菱形ABCD的对角线为AC和BD,E,F,G,H分别是AB,BC,CD,DA的中点,求证:E,F,G,H四个点在同一个圆上.图3-1-21【解析】 只要证明菱形的对角线交点O到菱形四边的中点E,F,G,H的距离相等,可以利用直角三角形斜边上的中线等于斜边的一半来证明OE=OF=OH=OG.
证明:设对角线AC,BD交于点O,连结OE,OF,OG,OH.【点悟】 要证明几个点在同一个圆上,就是证明这几个点到某一点的距离相等.另外证明四点共圆还有一些常用方法,学有余力的同学可以在课外进行探究. 1.若Rt△ABC的三个顶点A,B,C在⊙O上,求证:Rt△ABC斜边AB的中点是⊙O的圆心.
图3-1-22证明:∵△ABC是直角三角形,AB是斜边,
∴取AB中点M,则MC=MA=MB,
又∵OA=OB=OC,∴O是AB中点,
故M与O重合,即AB的中点是⊙O的圆心.2.如图3-1-23,△ABC和△ABD都为直角三角形,且∠C=∠D=90°.求证:A,B,C,D四点在同一个圆上.图3-1-23证明:取弦AB的中点O,连结OC,OD,
∵△ABC和△ABD都为直角三角形,且∠C=∠D=90°,
∴DO,CO分别为Rt△ABD和Rt△BCD斜边上的中线,
∴OA=OB=OC=OD.
∴A,B,C,D四点在同一个圆上.练 一 练
1.掌握确定圆的条件;
2.理解三角形的外接圆、圆的内接三角形,内心等概念;
3.会确定一个圆的圆心.
【学法指导】
1.对“不在同一直线上的三个点确定一个圆”的理解可以从过一个点的圆、过两个点的圆、过三个点的圆作图来理解;
2.三角形的外接圆有关的计算常与勾股定理、方程思想结合在一起;
3.分类讨论思想在讨论外心的位置时需要用到.填 一 填
1.不在同一直线上的三个点确定一个圆
(1)过一点的圆
经过平面上的一点A可以画无数个圆,圆心可以是平面上异于点A的任意一点.如图3-1-14(1)所示.
(2)过两点的圆
经过平面上的两点A,B可以画无数个圆,圆心一定在AB的垂直平分线上.如图3-1-14(2)所示.【知识管理】(3)过不在同一直线的三点的圆
经过平面上的三点A,B,C(不在同一直线上),可以作一个圆,并且只能作一个圆.如图3-1-14(3)所示.
图3-1-142.三角形的外接圆
定义:经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.图3-1-15如图3-1-15所示,⊙O经过△ABC的三个顶点A,B,C,那么,⊙O是△ABC的外接圆,点O是△ABC的外心,△ABC是⊙O的内接三角形.
外心:(1)三角形的外心是_______________________ _______的交点.
(2)三角形的外心到三角形____________________相等.
(3)锐角三角形的外心在三角形的_________,直角三角形的外心是____________________,钝角三角形的外心在三角形的________,反之也成立.三角形三条边的垂直平分线三个顶点的距离内部三角形的斜边中点外部
1.(知识点1)已知△ABC,若过点A、点B作圆,那么下面说法正确的是 ( )
A.这样的圆只能作出一个
B.这样的圆只能作出两个
C.点C不在该圆的外部,就在该圆的内部
D.圆心分布在AB的中垂线上【对点自测】D2.(知识点2)三角形的外心是三角形三边的________ ______的交点,它到三角形的___________的距离相等.
3.(知识点2)在△ABC中,∠C=90°,AC=8,BC=6,则△ABC的外接圆直径的长为_______.
4.(知识点1)已知直线a和直线外的两点A,B,经过A,B作一圆,使它的圆心在直线a上.图3-1-16垂直平分线三个顶点10解:作图如下:研 一 研类型之一 三角形的外接圆的有关概念及作图
例1 下列说法正确的是 ( )
A.经过三个点一定可以作圆
B.任意一个圆一定有内接三角形,并且只有一个内接三角形
C.任意一个三角形一定有一个外接圆,并且只有一个外接圆
D.三角形的外心到三角形各边的距离都相等C【解析】 过同一直线上的三点不能作圆,故A不正确;一个圆有无数多个内接三角形,故B不正确;三角形的外心是其三边垂直平分线的交点,所以三角形的外心到三个顶点的距离相等,故D不正确. 1.如图3-1-17,直角坐标系中一条圆弧经过格点A,B,C,其中,B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 ( )
图3-1-17CA.(2,1) B.(2,2)
C.(2,0) D.(2,-1)
【解析】作弦AB和BC的垂直平分线,交点即为圆心.如图所示,则圆心是(2,0).2.某地出土一个明代残破圆形瓷盘,为复制该瓷盘需确定其圆心和半径,请在图3-1-18中用直尺和圆规画出瓷盘的圆心(不要求写作法、证明和讨论,但要保留作图痕迹)图3-1-18解:在圆上取两个弦,作出两弦的垂直平分线即可.类型之二 三角形的外接圆的有关计算
例2 如图3-1-19所示,在△ABC中,AB=AC=10,BC=12,求△ABC的外接圆半径.图3-1-19【解析】 欲求△ABC外接圆的半径,关键找到圆心,由于△ABC是等腰三角形且AB=AC,作出BC边上的高AD,则圆心一定在AD上,设点O为外心,连结OB,在Rt△ODB中可求出半径.
解:过A作AD⊥BC,垂足为D,在AD上取一点O,连结OB,设O为△ABC外接圆圆心,且OA=OB=x.
∵△ABC为等腰三角形,AD⊥BC,【点悟】 构造直角三角形,设出未知数,利用勾股定理建立关于未知数的方程,是解决几何问题中线段长的常用方法. 如图3-1-20,已知△ABC,AB=AC=8,∠BAC=120°,请用圆规和直尺作出△ABC的外接圆.并计算此外接圆的半径.
图3-1-20解:画图如下:
∵AB=AC=8,∠BAC=120°,AO⊥BC,
∴∠BAO=60°,
∴△ABO为等边三角形,
∴△ABC的外接圆的半径为8.
类型之三 证明几个点在同一个圆上
例3 如图3-1-21所示,已知菱形ABCD的对角线为AC和BD,E,F,G,H分别是AB,BC,CD,DA的中点,求证:E,F,G,H四个点在同一个圆上.图3-1-21【解析】 只要证明菱形的对角线交点O到菱形四边的中点E,F,G,H的距离相等,可以利用直角三角形斜边上的中线等于斜边的一半来证明OE=OF=OH=OG.
证明:设对角线AC,BD交于点O,连结OE,OF,OG,OH.【点悟】 要证明几个点在同一个圆上,就是证明这几个点到某一点的距离相等.另外证明四点共圆还有一些常用方法,学有余力的同学可以在课外进行探究. 1.若Rt△ABC的三个顶点A,B,C在⊙O上,求证:Rt△ABC斜边AB的中点是⊙O的圆心.
图3-1-22证明:∵△ABC是直角三角形,AB是斜边,
∴取AB中点M,则MC=MA=MB,
又∵OA=OB=OC,∴O是AB中点,
故M与O重合,即AB的中点是⊙O的圆心.2.如图3-1-23,△ABC和△ABD都为直角三角形,且∠C=∠D=90°.求证:A,B,C,D四点在同一个圆上.图3-1-23证明:取弦AB的中点O,连结OC,OD,
∵△ABC和△ABD都为直角三角形,且∠C=∠D=90°,
∴DO,CO分别为Rt△ABD和Rt△BCD斜边上的中线,
∴OA=OB=OC=OD.
∴A,B,C,D四点在同一个圆上.练 一 练
同课章节目录
