3.2图形的旋转

课件35张PPT。3.2 图形的旋转【学习目标】
1．理解旋转的概念；
2．掌握旋转的性质；
3．会作一个图形的旋转图形．
?【学法指导】
1．学会从生活中的实例中抽象出旋转图形，概括旋转特征；
2．用运动的观点研究图形的旋转，学会用不变量的思想研究图形的运动．
1．旋转的概念
旋转：一般地，一个图形变为另一个图形，在运动过程中原图形上所有的点都绕一个固定的点，按同一个方向，转动同一个角度，这样图形运动叫做图形的旋转．固定的点叫做_____________，转动的角叫做___________．【知识管理】填 一 填旋转中心旋转角注意：(1)旋转中心是点，而不是直线，如生活中的开门、关门是绕轴旋转一定的角度．不属于我们研究的绕定点旋转；(2)经过旋转后，图形上任意一对对应点与旋转中心的连线所成的角都是旋转角．2．旋转的性质
性质：(1)对应到旋转中心的距离________；(2)对应点与旋转中心连线所成的夹角等于___________；(3)旋转前后的图形_________．
3．作旋转图形的一般步骤
步骤：(1)明确三个条件：旋转中心，旋转方向，旋转角度；
(2)确定关键点，作出关键点旋转后的对应点；
(3)顺次连结对应点．相等旋转角全等
1．(知识点2)旋转不改变图形的 (　 　)
A．大小和形状
B．位置和形状
C．位置和大小
D．位置、大小和形状【对点自测】A2．(知识点2)一个图形无论经过平移还是旋转，有以下说法：①对应线段平行；②对应线段相等；③对应角相等；④图形的形状和大小都没有发生变化．其中正确的是 (　 　)
A．①②③　　　　　　B．①②④
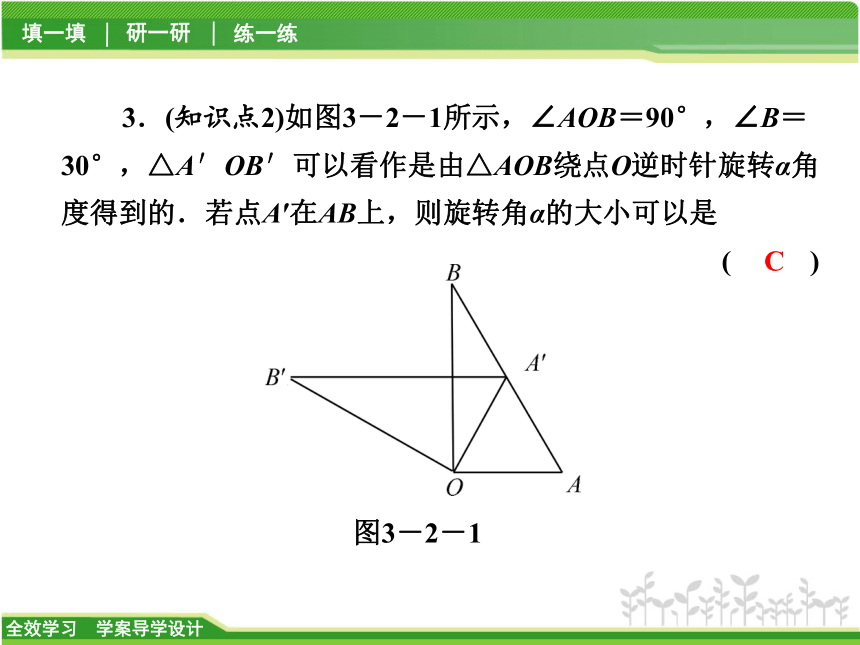
C．①③④ D．②③④D3．(知识点2)如图3－2－1所示，∠AOB＝90°，∠B＝30°，△A′OB′可以看作是由△AOB绕点O逆时针旋转α角度得到的．若点A′在AB上，则旋转角α的大小可以是
(　 　)图3－2－1CA．30° B．45°
C．60° D．90°
【解析】∵∠AOB＝90°，∠B＝30°，∴∠A＝60°.
∵△A′OB′可以看作是由△AOB绕点O逆时针旋转α角度得到的，
∴OA＝OA′.∴△OAA′是等边三角形．
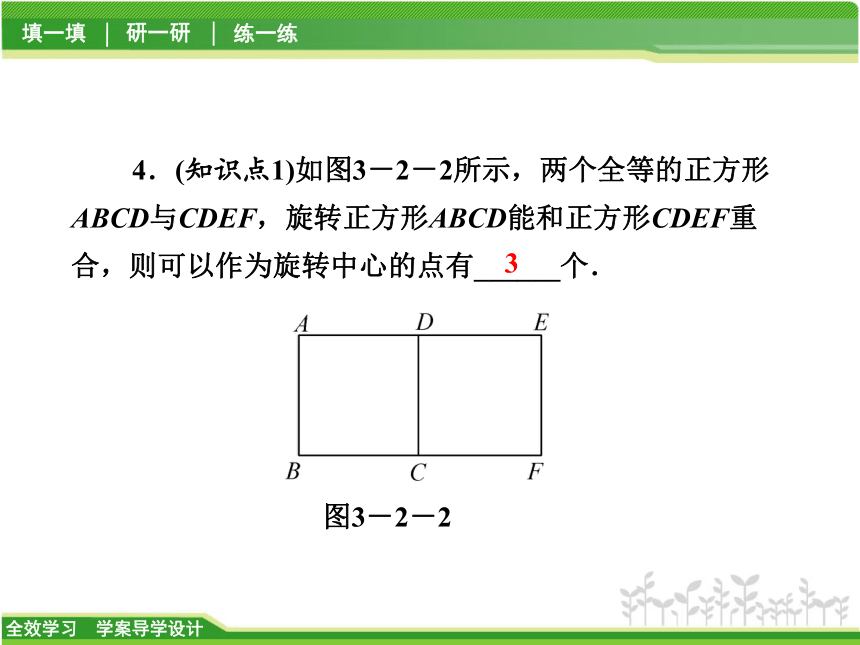
∴∠AOA′＝60°，即旋转角α的大小可以是60°.4．(知识点1)如图3－2－2所示，两个全等的正方形ABCD与CDEF，旋转正方形ABCD能和正方形CDEF重合，则可以作为旋转中心的点有______个．图3－2－23【解析】①以C为旋转中心，把正方形ABCD顺时针旋转90°，可得到正方形CDEF；
②以D为旋转中心，把正方形ABCD逆时针旋转90°，可得到正方形CDEF；
③以CD的中点为旋转中心，把正方形ABCD旋转180°，可得到正方形CDEF.
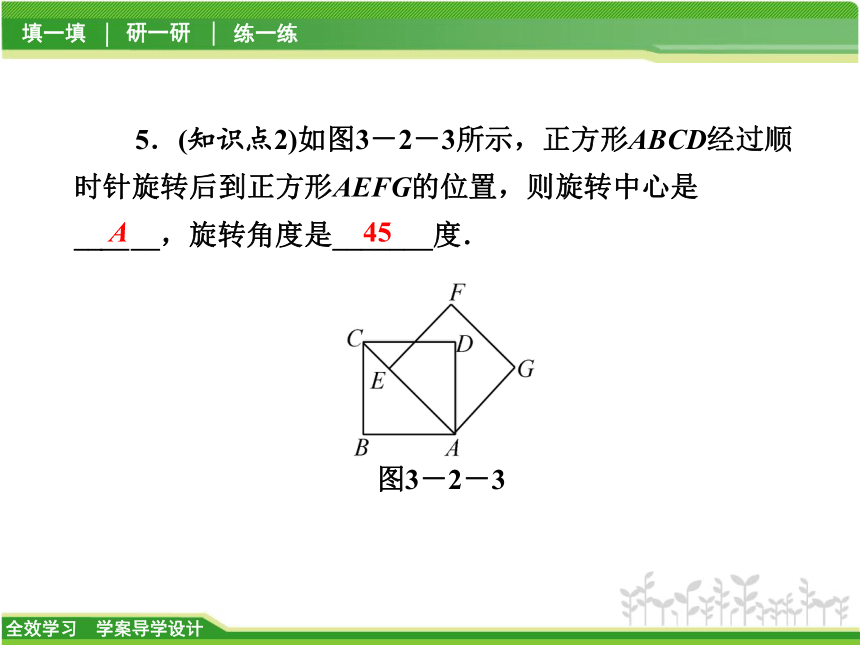
综上所述，可以作为旋转中心的点有3个；5．(知识点2)如图3－2－3所示，正方形ABCD经过顺时针旋转后到正方形AEFG的位置，则旋转中心是______，旋转角度是_______度．图3－2－3A45【解析】∵正方形ABCD经过顺时针旋转后得到正方形AEFG，∴旋转中心为点A，旋转角为∠CAB，
∵AC是正方形ABCD的对角线，∴∠CAB＝45°，
∴旋转角为45°.研 一 研类型之一　旋转及其性质
例1　如图3－2－4所示，在Rt△OAB中，∠OAB＝90°，OA＝AB＝6，将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.图3－2－4(1)线段OA1的长是______.∠AOB1的度数是________；
(2)连结AA1，求证：四边形OAA1B1是平行四边形；
(3)求四边形OAA1B1的面积．
【解析】(1)OA1＝OA＝6，∠AOB1＝∠A1OB1＋∠A1OA＝45°＋90°＝135°；
(2)证明OA綊A1B1；
(3)四边形OAA1B1的面积＝OA·OA1.
6135°解：(1)OA1＝OA＝6，∠AOB1＝∠A1OB1＋∠AOA＝45°＋90°＝135°
(2)证明：∵∠AOA1＝∠OA1B1＝90°，
∴OA∥A1B1，又OA＝AB＝A1B1，
∴四边形OAA1B1是平行四边形；
(3)四边形OAA1B1的面积＝OA·OA1＝6×6＝36.【点悟】(1)旋转前、后的图形全等，对应角、对应边相等；
(2)对应点与旋转中心连线所成的夹角等于旋转角． 1. 如图3－2－5所示，可以看作是一个等腰直角三角形旋转若干次而生成的图案，则每次旋转的度数可以是 (　 　)
图3－2－5CA．90°　　　　　　　　　B．60°
C．45° D．30°
【解析】∵中心角是由8个度数相等的角组成，∴每次旋转的度数可以为360°÷8＝45°.2．如图3－2－6，Rt△ABC是等腰三角形，D是Rt△ABC内一点，BC是斜边，如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置，则∠ADD′的度数是
(　 　)图3－2－6DA．25° B．30°
C．35° D．45°
【解析】∵将△ABD绕点A按逆时针方向旋转到△ACD′的位置，
∴AD＝AD′，∠DAD′＝∠BAC＝90°，即△ADD′是等腰直角三角形，
∴∠ADD′＝45°.类型之二　旋转作图
例2　如图3－2－7所示，已知四边形ABCD绕点O顺时针旋转一定角度后，使得点A落在点A′处，试作出旋转后的图形．图3－2－7解：图略．作法：
(1)连结OA，OA′.
(2)连结OB，OC，OD，分别以OB，OC，OD为始边，点O为顶点顺时针作∠BOB′，∠COC′，∠DOD′，并使得∠BOB′＝∠COC′＝∠DOD′＝∠AOA′，OB′＝OB，OC′＝OC，OD′＝OD.
(3)顺次连结A′，B′，C′，D′四点．
则四边形A′B′C′D′就是所要作的图形．【点悟】旋转作图的依据是图形上每一点都绕旋转中心沿相同的方向转动了相同的角度，对应点到旋转中心的距离相等，这是旋转的基本规律，也是我们作图的依据，对于旋转作图，应先确定图形的“关键点”，以局部带动整体进行旋转． (2012·安徽)如图3－2－8，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC(顶点是网格线的交点)和点A1.图3－2－8(1)画出一个格点△A1B1C1，并使它与△ABC全等且A与A1是对应点；
(2)画出点B关于直线AC的对称点D，并指出AD可以看作由AB绕A点经过怎样的旋转而得到的．
解：(1)如图所示，利用△ABC≌△A1B1C1，图形平移，可得出△A1B1C1；
(2)如图所示，AD可以看成是AB绕着点A逆时针旋转90°得到的．【点悟】本题应熟练掌握根据平移、轴对称、旋转的特征作图．类型之三　旋转证明
例3　如图3－2－9，正方形ABCD的边CD在正方形ECGF的边CE上，连结BE，DG.
(1)观察猜想BE与DG之间的大小关系，并证明你的结论；
(2)图中是否存在通过旋转能够互相重合的两个三角形？若存在，请说出旋转过程；若不存在，请说明理由．图3－2－9【解析】(1)根据正方形的性质找出满足△BCE≌△DCG的条件，得到△BCE≌△DCG，从而求出BE＝DG；
(2)将Rt△BCE绕点C顺时针旋转90°，可与Rt△DCG完全重合．解：(1)BE＝DG.
证明：在△BCE和△DCG中，
∵四边形ABCD和四边形ECGF都是正方形，
∴BC＝DC，EC＝GC，
∵∠BCE＝∠DCG＝90°，
∴△BCE≌△DCG，
∴BE＝DG；
(2)由(1)证明过程知：存在，是Rt△BCE和Rt△DCG，
将Rt△BCE绕点C顺时针旋转90°，可与Rt△DCG完全重合．
(或将Rt△DCG绕点C逆时针旋转90°，可与Rt△BCE完全重合)． 1.如图3－2－10，已知D为等边△ABC内一点，将△DBC绕点C旋转到△EAC的位置．试判断△CDE的形状，并证明你的结论．
图3－2－10解：△CDE为等边三角形．
证明：∵△EAC是由△DBC绕点C旋转而成，
∴∠ACE＝∠BCD，CD＝CE，
∴∠DCE＝∠BCA，
∵△ABC为等边三角形，∴∠ACB＝∠DCE＝60°，
∵CE＝CD，∴∠CED＝∠CDE＝60°，
∴△CDE为等边三角形．2．如图3－2－11，把正方形ABCD绕点A按顺时针方向旋转得到正方形AEFG，边FG与BC交于点H.求证：HG＝HB.图3－2－11证明：连结AH.
∵四边形ABCD和四边形AEFG都是正方形，
∴∠B＝∠G＝90°.
由题意知AG＝AB，
在Rt△AGH和Rt△ABH中，AH＝AH，AG＝AB，
∴Rt△AGH≌Rt△ABH(HL)，
∴HG＝HB.练 一 练