3.3 垂径定理

课件32张PPT。3.3 垂径定理第1课时 垂径定理【学习目标】
1．理解并掌握垂径定理；
2．会利用垂径定理解决实际问题．
【学法指导】
1．理解圆的对称性，利用对称性理解垂径定理；
2．在运用垂径定理求有关线段长度时有时需要分类讨论．填 一 填
1．圆的轴对称性
圆是_____________，每一条过圆心的直线都是圆的__________．【知识管理】轴对称图形对称轴注意：圆有无数条对称轴。2．垂径定理
定理：垂直于弦的直径_________这条弦，并且___________________．平分平分弦所对的弧说明：如图3－3－1所示，连结OA，OB，利用等腰三角形的性质也可证明定理．图3－3－13．弧的中点及弦心距弦心距：圆心到圆的___________________叫弦心距．如图3－3－1所示，OE是弦AB的弦心距．分一条弧一条弦的距离
1．(知识点2)已知⊙O的半径为5，弦AB的弦心距为3，则AB的长是 (　 　)
A．3　　　　　　　　B．4
C．6 D．8【对点自测】D2．(知识点3)在直径为10 cm的⊙O中，有长为5 cm的弦AB，则O到AB的距离等于 (　 　)D【解析】 如图所示，
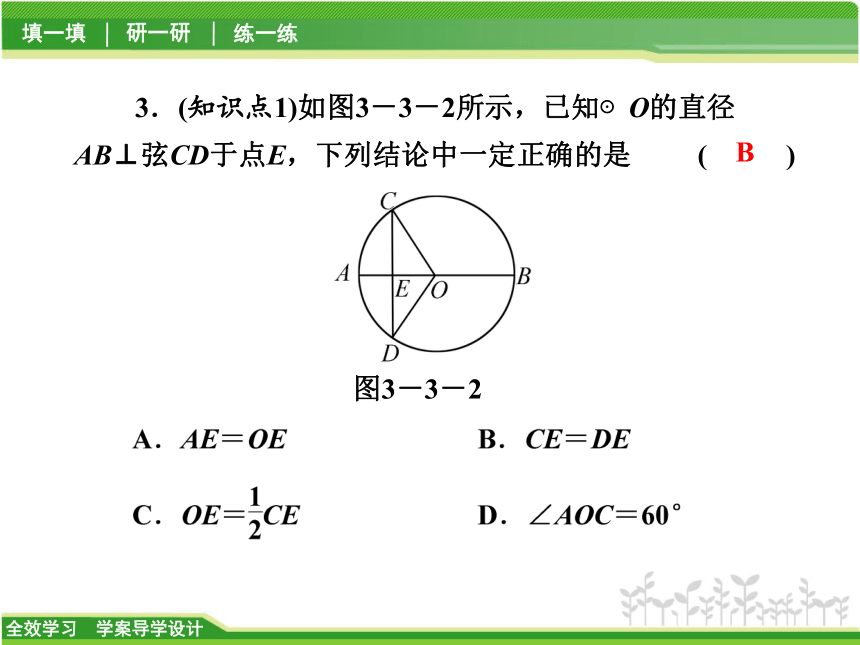
∵OC⊥AB于C，3．(知识点1)如图3－3－2所示，已知⊙O的直径AB⊥弦CD于点E，下列结论中一定正确的是 (　 　)图3－3－2B4．(知识点2)如图3－3－3所示，⊙O的半径为5，弦AB＝8，OC⊥AB于C，则OC的长等于______.图3－3－3【解析】 由垂径定理可得AC＝4，连结AO，如图所示，由勾股定理，得OC＝3.3研 一 研类型之一　垂径定理
例1　如图3－3－4所示，在Rt△ABC中，∠C＝90 °，AC＝5 cm，BC＝12 cm，以C为圆心，AC为半径的圆交斜边于D，求AD的长．图3－3－4【点悟】 遇到与弦有关的问题往往要过圆心作垂直于弦的直径． 1. 如图3－3－5，⊙O的直径CD＝10，弦AB＝8，AB⊥CD，垂足为M，则DM的长为______.图3－3－582．如图3－3－6所示，AB为⊙O的直径，且弦CD⊥AB于E，CD＝16，AE＝4，求OE的长．图3－3－6解：连结CO，如图所示，由AB⊥CD，AB为⊙O的直径，可得CE＝ED＝8.
在Rt△CEO中，CO2＝OE2＋CE2.
设OE＝x，则AO＝EO＋AE＝x＋4，
又CO＝AO＝x＋4，
所以(x＋4)2＝x2＋82，解得x＝6，即OE＝6.例2　已知圆的半径为13 cm，两弦AB∥CD，AB＝24 cm，CD＝10 cm，则两弦AB，CD的距离是 (　 　)
A．7 cm　　　　　　B．17 cm
C．12 cm D．7 cm或17 cmD(2)当圆心O在AB，CD之间时，如图(2)所示，过O作OE⊥AB于E，延长交CD于F，连结OC，OA，同样可得OF＝12，OE＝5.∴EF＝OE＋OF＝17.
所以，AB，CD之间的距离为7 cm或17 cm.【点悟】(1)本题主要是渗透分类思想，培养严密性思维和解题方法：确定图形——分析图形——数形结合——解决问题；(2)学会作辅助线的方法．图3－3－7证明：如图所示．作OG⊥AB，分别交AB，CD和圆于点E，F，G.2．如图3－3－8，在同一平面内，有一组平行线l1，l2，l3，相邻两条平行线之间的距离均为4，点O在直线l1上，⊙O与直线l3的交点为A，B，AB＝12，求⊙O的半径．图3－3－8类型之二　垂径定理在实际生活中的应用
例3　“圆材埋壁”是我国古代著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”答曰：“26寸”．
题目用现在的数学语言表达是：“如图3－3－9所示，CD是⊙O的直径，弦AB⊥CD，垂足为E，CE＝1寸，AB＝10寸，求直径CD的长．”图3－3－9【解析】 这是一道用垂径定理和勾股定理解决的题目．【点悟】 解决此类问题的关键是要由这一实际问题抽象出弦心距、弦长一半及半径构成的直角三角形这一几何模型． 1.如图3－3－10所示，是一个单心圆形隧道的截面，若路面AB宽为10 m，高CD为7 m，则此隧道单心圆的半径OA是 (　 　)
图3－3－10B练 一 练