3.4圆心角定理

课件34张PPT。3.4 圆心角第1课时 圆心角定理【学习目标】
1．理解圆的中心对称性和旋转不变性；
2．理解并掌握的圆心角的概念及圆心角定理；
3．理解1°的弧的概念；
4．会运用圆心角定理解决实际问题．
?【学法指导】
1．通过理解圆的旋转不变性，理解圆心角定理；
2．转化思想，把圆心角、弧、弦、弦心距利用圆心角定理进行互相转化．填 一 填
1．圆的中心对称性和旋转不变性
圆的中心对称性：圆是___________图形，圆心就是它的对称中心．
圆具有旋转不变的特性：把圆绕圆心旋转任意一个角度，所得的图形__________________．【知识管理】中心对称都和原图形重合2．圆心角的概念
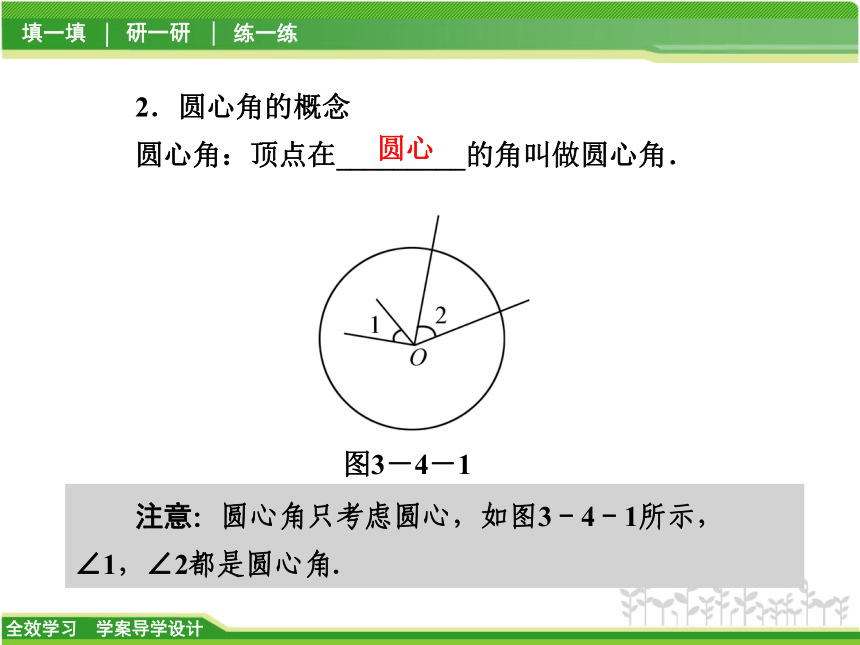
圆心角：顶点在_________的角叫做圆心角．图3－4－1圆心注意：圆心角只考虑圆心，如图3－4－1所示，∠1，∠2都是圆心角．3．圆心角定理
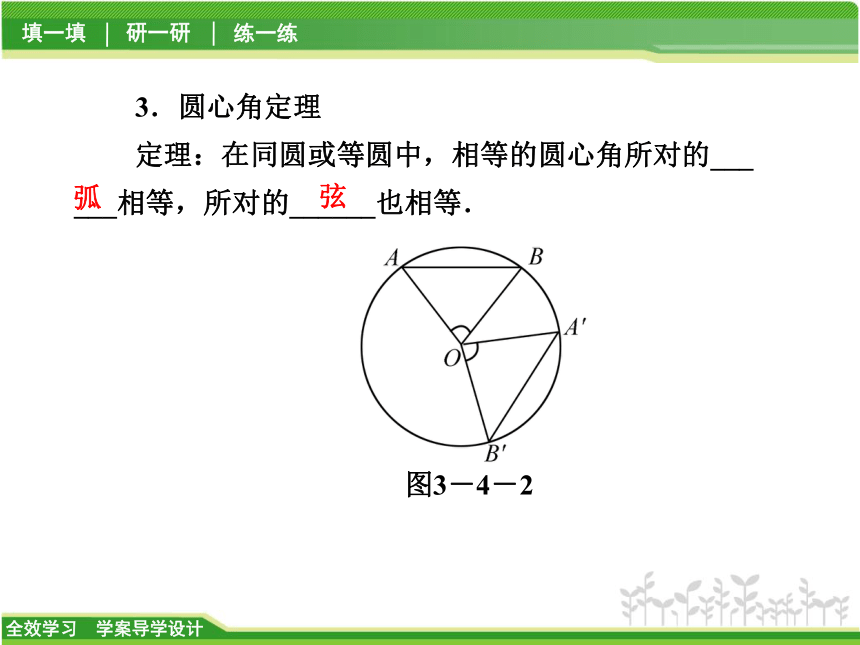
定理：在同圆或等圆中，相等的圆心角所对的___ ___相等，所对的______也相等．图3－4－2弧弦4．1 °的弧的概念
定义：1°圆心角所对的弧叫做1°的弧．这样，n°的圆心角所对的弧就是n°的弧．
说明：(1)1°的圆心角所对的是1°的弧，1°的弧所对的是1°的圆心角．
(2)圆心角的度数和它所对弧的度数相等．
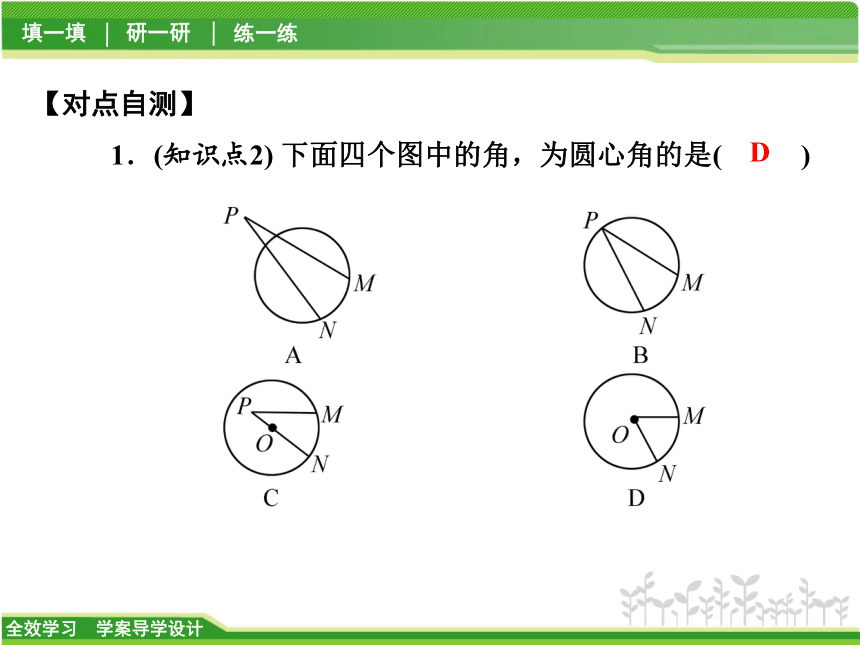
1．(知识点2) 下面四个图中的角，为圆心角的是(　 　)【对点自测】D2．(知识点2) 在半径为2 cm的⊙O中，弦长为2 cm的弦所对的圆心角为 (　 　)
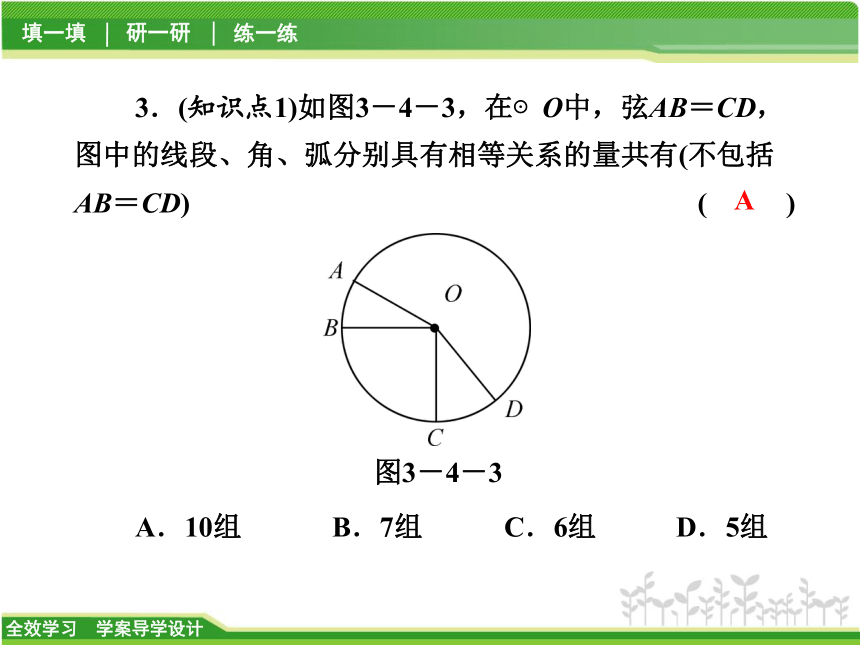
A．30°　　　B．60°　　C．90°　　D．120°【解析】如图，AB＝2，连结OA，OB，作OD⊥AB，垂足为D.则由垂径定理知，点D是AB的中点，AD＝1，而AO＝2，∴∠AOD＝30°，∴∠AOB＝60°.B3．(知识点1)如图3－4－3，在⊙O中，弦AB＝CD，图中的线段、角、弧分别具有相等关系的量共有(不包括AB＝CD) (　 　)图3－4－3A．10组 B．7组 C．6组 D．5组A图3－4－4C研 一 研类型之一　利用圆心角定理计算
例1　如图3－4－5所示，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O的内接正方形，BC∥QR，则∠AOQ等于 (　 　)
A．60°　　　　　　B．65°
C．72° D．75°图3－4－5D【点悟】 圆内接正三角形的圆心角等于120°.圆内接正方形的圆心角等于90°.本题利用“圆心角的度数和它所对的弧的度数相等”解题．A．40° B．65°
C．100° D．105°图3－4－6B2．如图3－4－7，△ABC是⊙O的内接正三角形，OD⊥BC于点D，则∠OCD＝ (　 　)图3－4－7A．30°　　B．60°　　C．45°　　　D．75°A类型之二　利用圆心角定理证明图3－4－8【点悟】 证明弧相等，常常证明它所对的圆心角相等．A．65° B．70°
C．75° D．80°图3－4－9D2．己知，如图3－4－10，AB，CD是⊙O的两条直径，弦CE∥AB，求证：AD＝AE.图3－4－10例3　如图3－4－11所示，△ABC是等边三角形，以BC为直径画⊙O交AB，AC于点D，E，求证：BD＝CE.图3－4－11【解析】 BD，CE是⊙O的两条弦，根据在同圆中，相等的圆心角所对的弧相等，所对的弦也相等这一结论，证明圆心角相等．
证明：连结OD，OE，∵△ABC是等边三角形，∴∠B＝60°.又∵OB＝OD，∴△BOD是等边三角形，∴∠BOD＝60°，同理∠COE＝60°，∴∠BOD＝∠COE，∴BD＝CE.(此题也可以通过过点O作OM⊥BD，ON⊥CE，垂足分别为M，N来证明)．
【点悟】 证明弦相等，往往转化为证明弧相等或圆心角相等．图3－4－12图3－4－13练 一 练