浙教版数学七年级上册 2.3有理数的乘法第1课时有理数的乘法课件(24张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 2.3有理数的乘法第1课时有理数的乘法课件(24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 772.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-12 10:04:51 | ||
图片预览





文档简介
(共24张PPT)
第2章 有理数的运算
2.3 有理数的乘法
第1课时 有理数的乘法
复习回顾
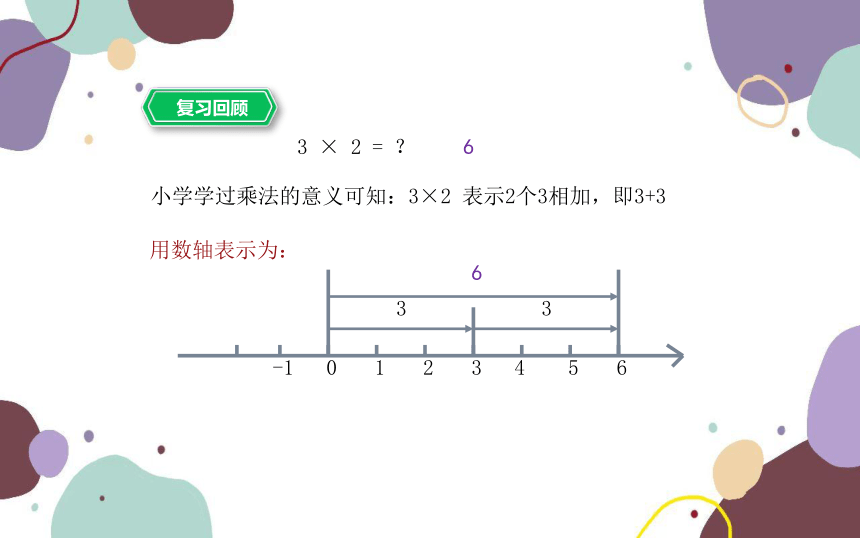
3 × 2 = ?
小学学过乘法的意义可知:3×2 表示2个3相加,即3+3
用数轴表示为:
0
1
2
3
4
5
6
-1
6
3
3
6
思考探究
类比有理数加法,两个有理数相乘 a×b, 有哪些情况
① 两数同正
② 两数异号
③ 两数同负
④至少一个因数为零
①同正两数相乘,如
②异号两数相乘, 如
③
同负两数相乘,如
(-2)×(-3)= ?
2 ×(-3)= ?
2 × 3 = 6
④与零相乘, 如
(-2)× 0 = ?
思考探究
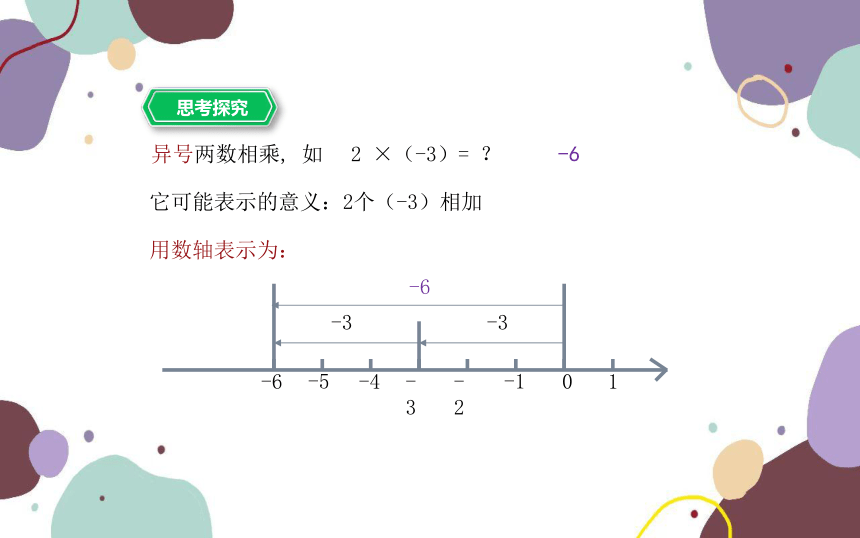
异号两数相乘, 如
2 ×(-3)= ?
用数轴表示为:
它可能表示的意义:2个(-3)相加
-6
-5
-4
-3
-2
-1
0
-6
-3
-3
1
-6
思考探究
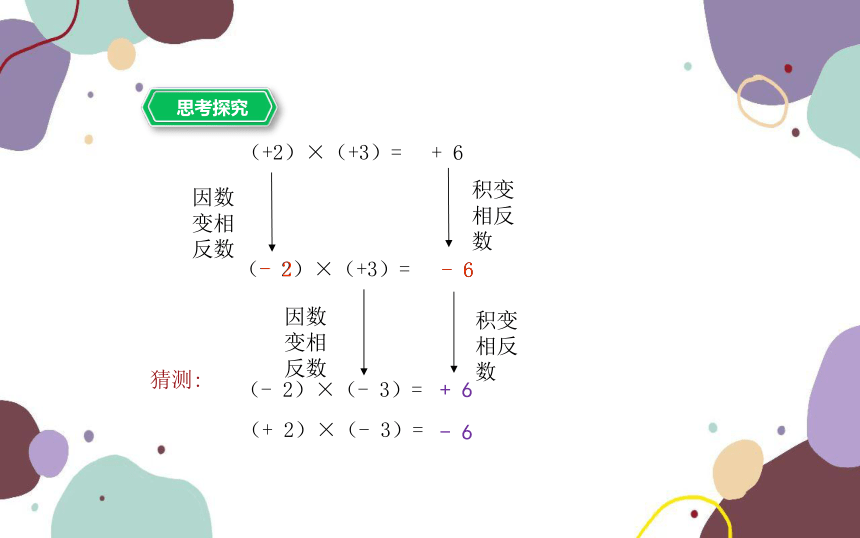
(+2)×(+3)=
+ 6
(- 2)×(+3)=
- 6
(- 2)×(- 3)=
+ 6
(+ 2)×(- 3)=
- 6
因数变相反数
积变相反数
猜测:
- 2
- 6
因数变相反数
积变相反数
新课讲解
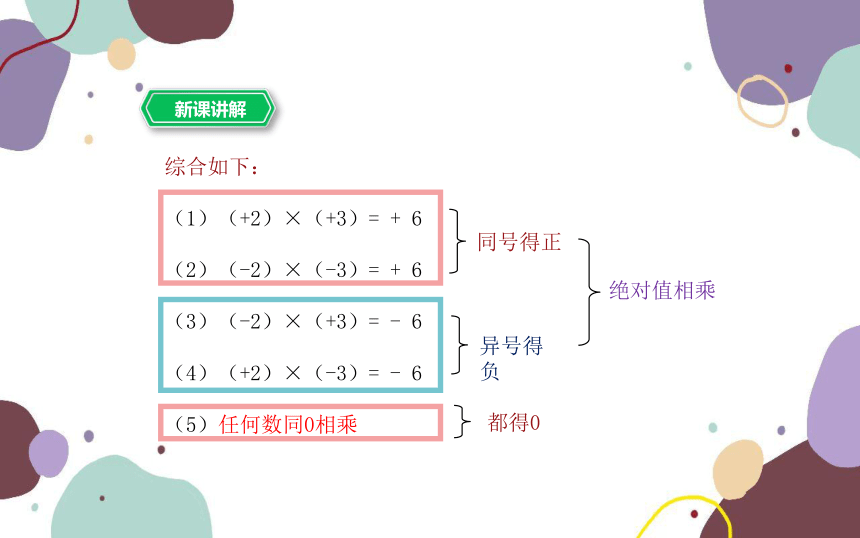
综合如下:
(1)(+2)×(+3)= + 6
(2)(-2)×(-3)= + 6
(3)(-2)×(+3)= - 6
(4)(+2)×(-3)= - 6
(5)任何数同0相乘
同号得正
异号得负
绝对值相乘
都得0
新课讲解
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,都得0。
有理数乘法法则:
由以上几个式子我们可以得知:
巩固练习
1、确定下列积的符号:
(1) 5×(-3)
(2) (-4)×6
(3) (-7)×(-9)
(4) 0.5×0.7
积的符号为负
积的符号为负
积的符号为正
积的符号为正
巩固练习
2、用“>” “<” “=”号填空
(1)( - 4)×(- 7 ) 0
<
>
=
(2)( - 5)×(+ 4) 0
<
例题讲解
例1 计算:
先确定积的符号
再把绝对值相乘
(2) (+1.75)×( 16)
= 28
运算中的
第一步是
______________。
第二步是
______________。
(1)
解:
解:
巩固练习
(4×5)
(7×7)
(4×9)
(5×7)
-
-
-
+
= - 20
= 35
= -49
= -36
计算:
1. (-4) ×5=
2. (-5) ×(-7)=
3. 7 ×(-7)=
4. (+4) ×(-9)=
多个不为0的有理数相乘时的运算步骤
先确定积的符号;
再进行绝对值的乘法运算
新课讲解
若其中一个乘数为0,则积为0。
计算下列各题,你发现什么?
1.(- 1)×2 ×(- 3)
2. (- 1)×2 ×(- 3) ×4
3. (-1)×2 ×(-3)×4 ×(-5)
几个不等于0的数相乘,积的符号由负因数的个数决定;
负因数的个数为奇数时,积为负;
负因数的个数为偶数时,积为正。
思考探究
=6
=24
= -120
观察下列各式,它们的积大于零、小于零、还是等于零?
(1)(-1) ×2 ×3 ×4
(2) (-1) ×(-2 )×3 ×4
(3) (-1) ×(-2 )×(-3 )×4
(4) (-1) ×(-2 )×(-3 )×(-4)
(5) (-1) ×(-2 )×(-3 )×(-4)×0
巩固练习
<0
<0
>0
>0
= 0
思考归纳
0
-3
一个数与1相乘,积为它本身;
一个数与(-1)相乘,积为它的相反数。
你发现了什么?
思考归纳
1
1
1
1
这些运算中,它们的积有什么共同特点
积都是1
新课讲解
0没有倒数。
注意:
例题讲解
分析:欲求某数的倒数,就是要确定与这个数相乘积为1的数是什么。
求小数的倒数时,要先把小数化成分数;
求带分数的倒数时,要先把带分数化成假分数。
注意:
例题讲解
解:
(1)∵
∴- 3的倒数是 。
(2)∵
∴ 的倒数是 。
(3)∵ 0.2
∴ 0.2的倒数是5。
求下列数的倒数:
(2)求分数的倒数,先把带分数化成假分数,
只要把假分数的分子,分母颠倒位置即可。
(1)互为倒数的两个数符号相同。
求倒数的时候要注意:
1
巩固练习
原数 1 -8 -7
倒数
课堂小结
1、有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同零相乘都得零。
特别地:
一个数与1相乘,积为它本身;
一个数与(-1)相乘,积为它的相反数。
4、若两个有理数的乘积为1,则这两个有理数互为倒数,(零没有倒数)。
3、几个有理数相乘,积的符号由负因数的个数决定
2、有理数乘法的一般步骤:
先确定积的符号,再把绝对值相乘。
课堂小结
奇数个为负,偶数个为正。
拓展练习
1、若a的相反数是1.5,则a的倒数为( )
2、两个有理数和为0,积为负,则这两个数的关系是( )
A 两个数均为0, B 两个数中一个为0
C 两数互为相反数, D 两数互为相反数,但不为0。
D
谢 谢!!
第2章 有理数的运算
2.3 有理数的乘法
第1课时 有理数的乘法
复习回顾
3 × 2 = ?
小学学过乘法的意义可知:3×2 表示2个3相加,即3+3
用数轴表示为:
0
1
2
3
4
5
6
-1
6
3
3
6
思考探究
类比有理数加法,两个有理数相乘 a×b, 有哪些情况
① 两数同正
② 两数异号
③ 两数同负
④至少一个因数为零
①同正两数相乘,如
②异号两数相乘, 如
③
同负两数相乘,如
(-2)×(-3)= ?
2 ×(-3)= ?
2 × 3 = 6
④与零相乘, 如
(-2)× 0 = ?
思考探究
异号两数相乘, 如
2 ×(-3)= ?
用数轴表示为:
它可能表示的意义:2个(-3)相加
-6
-5
-4
-3
-2
-1
0
-6
-3
-3
1
-6
思考探究
(+2)×(+3)=
+ 6
(- 2)×(+3)=
- 6
(- 2)×(- 3)=
+ 6
(+ 2)×(- 3)=
- 6
因数变相反数
积变相反数
猜测:
- 2
- 6
因数变相反数
积变相反数
新课讲解
综合如下:
(1)(+2)×(+3)= + 6
(2)(-2)×(-3)= + 6
(3)(-2)×(+3)= - 6
(4)(+2)×(-3)= - 6
(5)任何数同0相乘
同号得正
异号得负
绝对值相乘
都得0
新课讲解
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,都得0。
有理数乘法法则:
由以上几个式子我们可以得知:
巩固练习
1、确定下列积的符号:
(1) 5×(-3)
(2) (-4)×6
(3) (-7)×(-9)
(4) 0.5×0.7
积的符号为负
积的符号为负
积的符号为正
积的符号为正
巩固练习
2、用“>” “<” “=”号填空
(1)( - 4)×(- 7 ) 0
<
>
=
(2)( - 5)×(+ 4) 0
<
例题讲解
例1 计算:
先确定积的符号
再把绝对值相乘
(2) (+1.75)×( 16)
= 28
运算中的
第一步是
______________。
第二步是
______________。
(1)
解:
解:
巩固练习
(4×5)
(7×7)
(4×9)
(5×7)
-
-
-
+
= - 20
= 35
= -49
= -36
计算:
1. (-4) ×5=
2. (-5) ×(-7)=
3. 7 ×(-7)=
4. (+4) ×(-9)=
多个不为0的有理数相乘时的运算步骤
先确定积的符号;
再进行绝对值的乘法运算
新课讲解
若其中一个乘数为0,则积为0。
计算下列各题,你发现什么?
1.(- 1)×2 ×(- 3)
2. (- 1)×2 ×(- 3) ×4
3. (-1)×2 ×(-3)×4 ×(-5)
几个不等于0的数相乘,积的符号由负因数的个数决定;
负因数的个数为奇数时,积为负;
负因数的个数为偶数时,积为正。
思考探究
=6
=24
= -120
观察下列各式,它们的积大于零、小于零、还是等于零?
(1)(-1) ×2 ×3 ×4
(2) (-1) ×(-2 )×3 ×4
(3) (-1) ×(-2 )×(-3 )×4
(4) (-1) ×(-2 )×(-3 )×(-4)
(5) (-1) ×(-2 )×(-3 )×(-4)×0
巩固练习
<0
<0
>0
>0
= 0
思考归纳
0
-3
一个数与1相乘,积为它本身;
一个数与(-1)相乘,积为它的相反数。
你发现了什么?
思考归纳
1
1
1
1
这些运算中,它们的积有什么共同特点
积都是1
新课讲解
0没有倒数。
注意:
例题讲解
分析:欲求某数的倒数,就是要确定与这个数相乘积为1的数是什么。
求小数的倒数时,要先把小数化成分数;
求带分数的倒数时,要先把带分数化成假分数。
注意:
例题讲解
解:
(1)∵
∴- 3的倒数是 。
(2)∵
∴ 的倒数是 。
(3)∵ 0.2
∴ 0.2的倒数是5。
求下列数的倒数:
(2)求分数的倒数,先把带分数化成假分数,
只要把假分数的分子,分母颠倒位置即可。
(1)互为倒数的两个数符号相同。
求倒数的时候要注意:
1
巩固练习
原数 1 -8 -7
倒数
课堂小结
1、有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同零相乘都得零。
特别地:
一个数与1相乘,积为它本身;
一个数与(-1)相乘,积为它的相反数。
4、若两个有理数的乘积为1,则这两个有理数互为倒数,(零没有倒数)。
3、几个有理数相乘,积的符号由负因数的个数决定
2、有理数乘法的一般步骤:
先确定积的符号,再把绝对值相乘。
课堂小结
奇数个为负,偶数个为正。
拓展练习
1、若a的相反数是1.5,则a的倒数为( )
2、两个有理数和为0,积为负,则这两个数的关系是( )
A 两个数均为0, B 两个数中一个为0
C 两数互为相反数, D 两数互为相反数,但不为0。
D
谢 谢!!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
